应用惯性释放方法的静气动弹性发散分析
章飞,程芳
(1.中航西飞民用飞机有限责任公司工程技术中心,西安710089)
(2.航空工业第一飞机设计研究院强度设计研究所,西安710089)
0 引 言
发散属于静气动弹性稳定性问题,它是由结构弹性力与定常气动力之间的相互耦合产生的,在飞行器设计中应该避免这种现象。杜子亮等对静气弹分析常用的柔度法和模态法进行了介绍,并提出模态影响系数的概念来评估模态的选取对气动弹性分析的影响;万志强等对常用的发散分析方法进行了介绍,从理论上证明了柔度法、模态法和颤振法三种方法的一致性,并和模型风洞试验结果进行了对比。但是传统的机翼静气弹问题通常只考虑机翼的刚度,并不涉及机翼、机身、尾翼的质量和惯量特性,约束时通常将机翼根部固支。然而,实际上飞机在自由飞行时并不能全都处理成这种约束方式。由于飞机存在刚体模态,气动力的扰动不仅会引起弹性力的变化,同时还会导致出现附加惯性力。因此,机翼根部固支的约束方式只有在机身的质量和绕各轴的惯量远大于机翼时是适用的。有些飞机的机翼(含短舱、发动机)质量并不比其他部件的质量总和小很多,因此,发散分析需要考虑惯性力的影响。
根据咨询通告 AC 25.629-1B第 7.1.2.3 节的要求,升力面发散分析需要考虑刚体模态自由度的影响,因为刚体模态或短周期模态也可能会造成发散。但是自由飞行的飞机是无约束的,无法直接求解结构静力或动力问题,需要利用结构的惯性力来平衡外力,消除方程的奇异性,从而求解结构方程。这种方法称之为惯性释放。
本文通过对惯性释放方法的研究,给出考虑刚体模态的模态法发散分析方法,以某型飞机为例,计算考虑刚体模态的气动弹性发散结果,与常用的静气动弹性发散结果进行对比,并分析不同燃油、商载情况对发散计算结果的影响。
1 应用惯性释放的发散分析方法
1.1 惯性释放分析方法
参考文献[13-17]的惯性释放方法,不考虑结构阻尼,飞机结构动力学方程为

m
、k
、x
、f
分别为质量矩阵、刚度矩阵、节点位移向量和外载荷向量。对方程(1)进行正则模态分析,得到模态坐标下的结构动力学方程:

M
、K
、u
、F
分别为广义质量矩阵、广义刚度矩阵、广义位移向量和广义外载荷向量。其中,

Φ
为模态振型矩阵,表征振动形态。自由—自由的飞机模态由刚体运动模态和弹性模态组成,其广义位移分别用u
和u
来表示,则方程(2)可表达成以下形式:
1.2 发散速压计算方法
考虑了惯性释放的静气动弹性方程为

q
为来流速压;A
为零频下弹性模态广义气动力系数矩阵。在发散速压q
处,方程(14)奇异,应满足: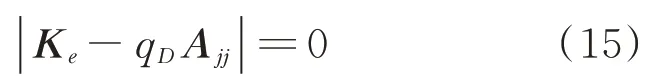
方程(15)可最终转化为如下特征值问题:
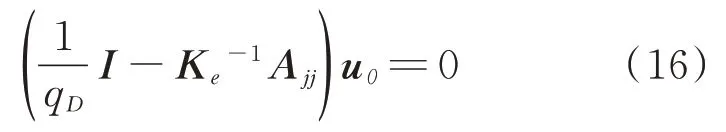
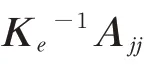
2 算例与分析
2.1 模 型
以某型民用飞机为例,对于能够准确计算剖面刚心和刚度的部件,如机身、机翼、垂尾、平尾等,直接建立单梁模型;而对于翼身连接区等难以准确计算刚度的区域,采用减缩刚度矩阵的形式来模拟其刚度特性。发散计算的非定常气动力采用亚声速偶极子格网法模拟,全机气动模型如图1所示,机翼、平尾、垂尾都简化为升力面,机身和发动机简化为细长体和干扰体。

图1 全机气动力模型Fig.1 Aerodynamic model of the entire aircraft
采用软件MD Nastran 2010.1 进行振动和气动力计算并提取相关质量、刚度和气动力系数矩阵。计算时取海平面空气密度为1.225 kg/m。
零高度时,根据气动弹性稳定性边界确定的发散临界速度(v
)要求为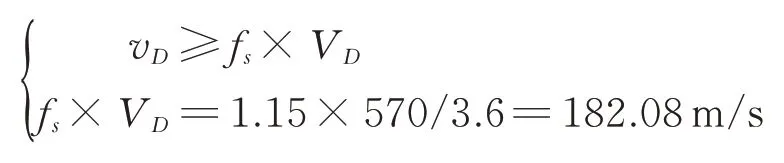
v
≥ 182.08 m/s,其中,f
=1.15,为条款要求的速度安全系数。2.2 空机状态发散分析
采用软件MD Nastran 2010.1 进行模态分析,取前64 阶自由—自由的弹性模态,主要模态及频率参数如表1 所示。
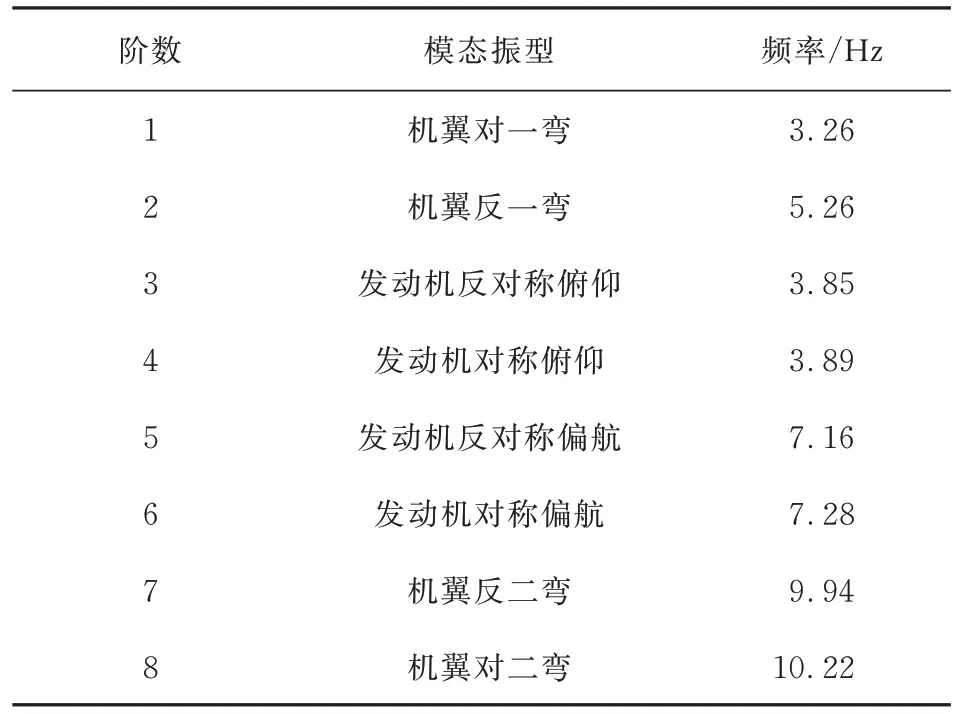
表1 主要模态参数Table 1 Parameters of main modes
对使用空机状态,分别按照考虑刚体模态的模态法(即第1 节的应用惯性释放的发散分析方法,后文中的考虑刚体模态的模态法发散分析皆指此方法)和不带刚体模态的模态法计算发散速度。最低的发散速度为453.8 m/s,为机翼对称一弯发散(根据特征向量确定)。分别进行考虑/不考虑刚体模态的颤振分析,其V
-g
-F
曲线如图2所示,图中给出最低两支频率掉零的模态,分别为机翼对一弯和发动机对俯仰,V
-g
曲线穿越g
=0线的速度即为发散速度。可以看出:最低发散速度为453.9 m/s,与模态法结果基本一致。发散模态同样为机翼对称一弯发散,计算结果如表2所示。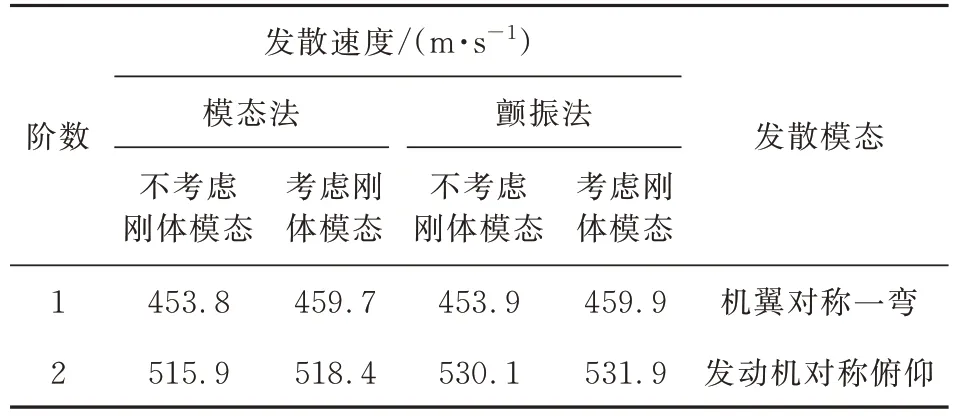
表2 空机状态全机发散速度计算结果Table 2 Calculation results of divergence speed in empty aircraft


图2 使用空机状态V-g-F 曲线Fig.2 V-g-F curve of empty aircraft
2.3 变燃油质量发散分析
在商载为0 的情况下分别采用模态法和颤振法进行燃油质量对全机的发散特性影响分析,选取的燃油质量为 900、1 950、3 070 及 5 000 kg。计算结果如表3 所示,可以看出:临界发散速度随机翼燃油质量的增大略有减小。
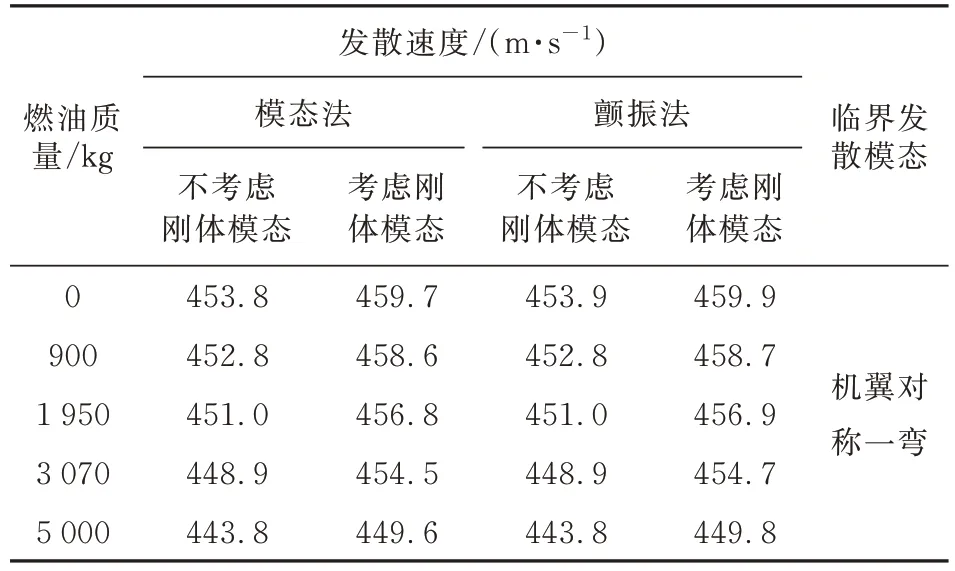
表3 燃油质量对发散速度影响分析结果Table 3 Influence of fuel weight on divergence speed
2.4 变商载质量发散分析
在燃油质量为0 的情况下采用模态法和颤振法进行商载质量对全机的发散特性影响分析,选取4 种典型商载质量进行变参数分析。计算结果如表4 所示,可以看出:临界发散速度随商载质量的增大略微降低。

表4 商载质量对发散速度影响分析结果Table 4 Influence of payload on divergence speed
2.5 结果分析
在相同的燃油或者商载质量下,考虑刚体模态后的发散速度高于不考虑刚体模态的发散速度;增加燃油质量后发散速度有所减小,增加商载后发散速度小幅降低;临界发散模态为机翼对称一弯发散,且不随燃油或商载的变化而变化。
3 结 论
(1)考虑刚体模态后的发散速度有所提高,但临界发散模态不变,仍为机翼对称一弯发散。
(2)发散速度随燃油质量的增加略有减小,随商载质量的增加小幅降低。
(3)本文通过惯性释放方法求解发散速度只考虑了刚体模态惯性的影响,未考虑弹性模态和刚体模态之间的气动耦合影响,这将在未来进一步展开研究。

