涡升力乘波体发展研究综述

易怀喜，王逗，李珺，罗世彬

（中南大学航空航天学院，长沙410083）

0 引 言

近年来，水平起降的可重复使用高超声速空天飞行器成为研究的热点。其飞行剖面需历经低速起降、亚跨超加减速以及高超声速巡航，因此，如何让飞行器在如此宽的速域范围内保持良好的气动性能是高超声速空天飞行器研究的难点。此外，随着飞行马赫数提高到高超声速，传统气动外形的升阻比很难进一步提高，而乘波飞行器利用激波贴体，比传统飞行器具有更好的高超声速气动性能。虽然乘波体在设计状态下的气动优势明显，但在非设计点很难保持。因此，若要将乘波体应用于高超声速空天飞行器的设计，适应宽速域飞行是其必须解决的问题。这里的宽速域有两层含义，第一是高超声速范围内的宽速域，即在非设计点的其他高超声速状态下飞行也能维持较好的气动性能，这一方向的研究较多，主要有多级、组合拼接、变马赫数或激波角、多马赫数星体、变型等设计方法；第二是低速到高超声速范围的宽速域，如何改善乘波体在低速时的气动特性是这一研究方向的重点，也是实现空天飞行器的关键，但目前在该领域的研究较少，比较有代表性的是“涡升力”乘波体。该类乘波体在低速时由前缘产生的漩涡在上表面形成低压区，从而在很大程度上改善了低速起飞阶段的气动性能，为乘波体的宽速域飞行提供了一种可行的、具有创新的思路。

本文对涡升力乘波体的设计方法及宽速域气动特性进行总结，分析设计方法的优缺点，并展望涡升力乘波体的后续发展方向。

1 涡升力乘波体设计原理和方法

“涡升力”乘波体的概念首先由洛克希德·马丁公司 的 P.E.Rodi提出，基于吻 切锥的 方法设计给定平面形状的乘波体。段焰辉等在此基础上给出固定前缘后掠角的乘波设计；宋赋强等研究大前缘后掠角乘波体在背风面的前缘涡，设计了一种大后掠角外形的宽速域乘波体；Zhao Z T 等利用吻切锥的乘波设计指定“三角翼”布局和“尖头”布局的涡升力乘波体；刘传振等类比“边条翼”布局，提出能够指定两个前缘后掠角的双后掠乘波布局的设计方法；陈冰雁等研究了基于激波装配法的波导体乘波体设计，并设计了具有双后掠前缘特征的乘波体；李永洲等提出一种前后缘型线同时可控的乘波设计，采用不同混合函数对下表面进行修型处理；李珺等系统地研究了基于投影法的双后掠乘波体气动性能。

涡升力乘波体的设计原理可总结为通过定制前缘线平面形状，使乘波前缘在低速下产生前缘漩涡，从而获得前缘涡带来的升力效益。其设计方法可归为三大类：基于吻切理论的定前缘型线法、基于激波装配法的波导体法和基于给定激波面的投影法。三种方法各有优势和一定的局限性，本节分别综述三种设计方法在涡升力乘波体设计上的相关研究。

1.1 基于吻切理论的定前缘型线法

在楔导法、锥导法与吻切锥法等乘波体的设计方法中，吻切锥法得益于优异的设计灵活性，被广泛应用于乘波体设计。相较于其他两种涡升力乘波体设计方法，基于吻切理论的定前缘型线法在涡升力乘波体设计中应用较多，其研究也较为详细。四种涡升力乘波体的具体设计方法虽然有所不同，但利用吻切锥法构造特定的乘波前缘的本质相同。本节总结基于吻切理论的定前缘型线法在定后掠角乘波体、三角翼乘波体、尖头翼乘波体和双后掠乘波体的设计原理。

（1）定后掠角乘波体设计

2005 年洛克希德·马丁公司的 P.E.Rodi从吻切锥理论出发，提出了能够指定平面形状的乘波体设计方法（如图1 所示），研究了前缘后掠角

λ

、长

L

、半宽

s

、有效激波角

β

和上表面与激波型线之间的夹角

γ

等特征参数之间的数学关系，如式（1）和式（2）所示。

图1 底部和前部视角下乘波前缘线上两点（A 和B）［21］Fig.1 Top view and front view of two points（A and B）along the waverider’s leading edge［21］

随后，段焰辉等在此基础上指出要得到具有一定后掠角

λ

的直线前缘，必须保证前缘对应的激波面和激波出口型线都是平面，并据此提出了定后掠角乘波体的设计方法。其中一种弯头定后掠乘波体的设计如图2 所示，其上表面后缘型线

OE

与激波出口型线的

AE

段都是直线，它们之间的夹角

γ

与后掠角

λ

、激波角

β

的关系也满足式（2）。激波出口型线的

RA

段则是与

AE

相切的圆弧，它对应于乘波体的弯头部分

VM

。

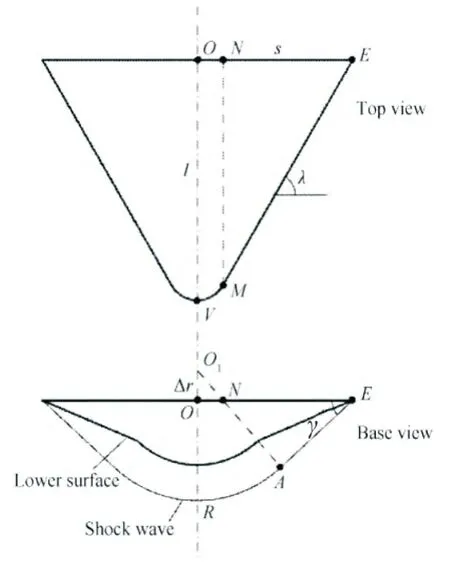
图2 定后掠角乘波体设计基本型线几何关系［23］Fig.2 Geometric relationship of basic profile for waverider with constant angle of sweepback［23］

（2）尖头乘波体和三角翼乘波体设计

国防科技大学的Zhao Z T 等采用吻切锥乘波体设计法，提出了三角翼乘波体布局（Deltawinged waverider）和尖头乘波体布局（Cuspidal waverider），设计原理如图 3～图4 所示。

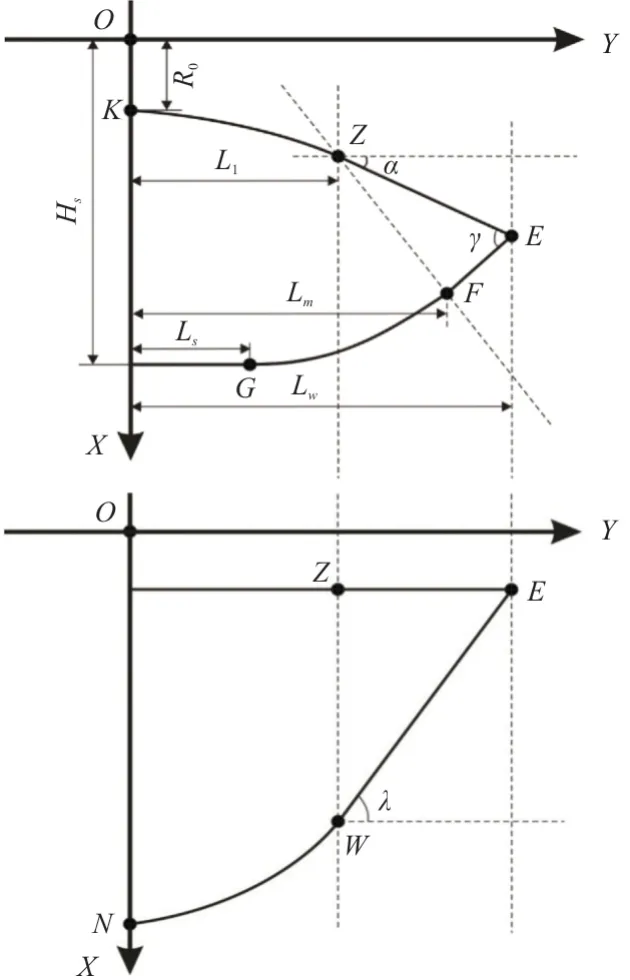
图3 三角翼乘波体设计原理［25］Fig.3 Design principle of the delta-winged waverider［25］

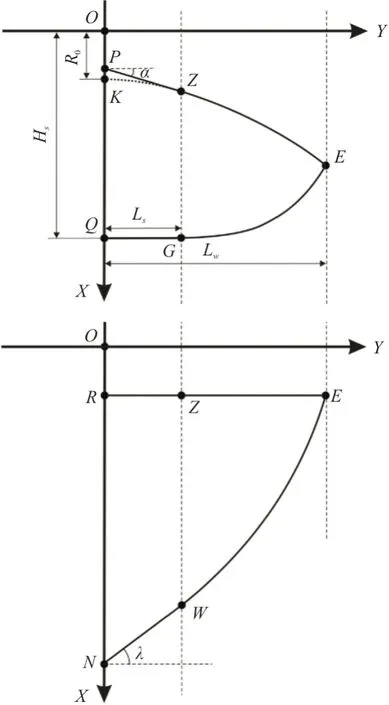
图4 尖头乘波体设计原理［25］Fig.4 Design principle of the cuspidal waverider［25］

与定后掠角乘波体（图2）相比，这两类乘波体的上表面后缘型线已不再限制为水平线了。三角翼乘波体在翼尖附近具有后掠角

λ

，而尖头乘波体则是在头部附近具有后掠角

λ

。三角翼和尖头前缘部分对应的前缘型线（图3 的

WE

与图4 的

WN

）、上表面后缘型线（图 3 的

ZE

与图 4 的

ZP

，它们与水平面的夹角记为

α

）与激波出口型线（图3 的

EF

和图4 的

QG

）均为直线。对于三角翼，三者之间满足几何关系式（3），而对于尖头前缘，则满足关系式（4）。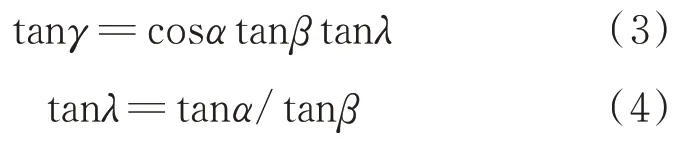

以上两类乘波体的非等后掠角部分所对应的前缘型线、上表面后缘型线和激波出口型线为曲线，且与各自型线上的直线段部分相切。

（3）双后掠乘波体设计

刘传振等利用吻切锥法乘波设计的灵活性，提出了定前缘型线法双后掠乘波体设计，原理如图5 所示，其第一后掠角和第二后掠角分别为

λ

、

λ

，

θ

和

θ

为 ICC 曲线偏转角。以上各参数满足关系式（5）～式（6）。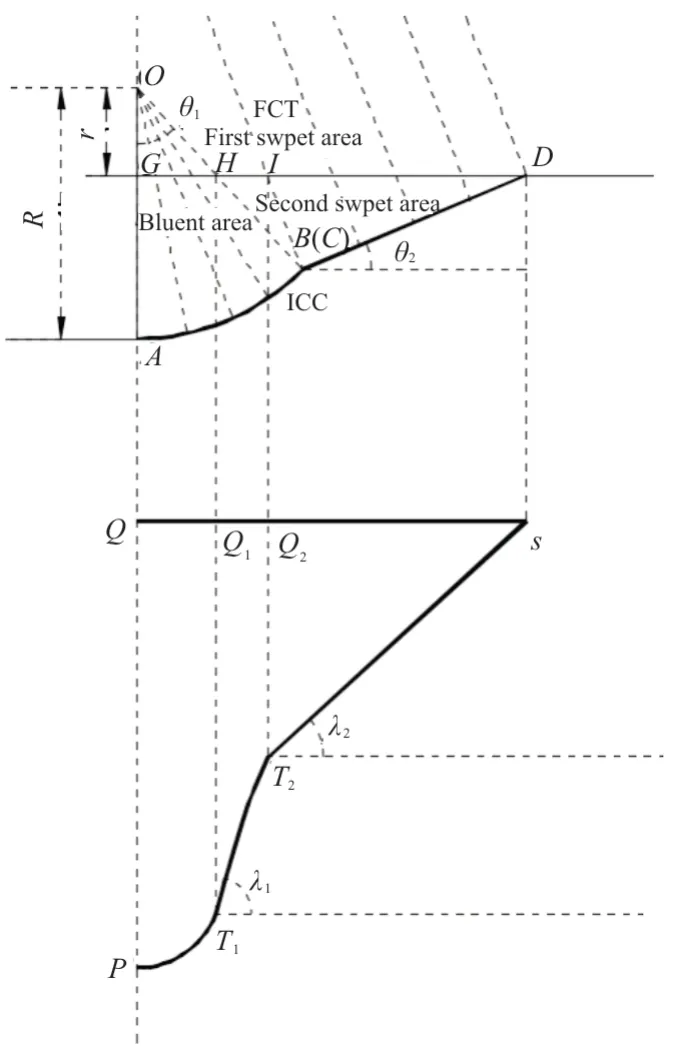

图5 双后掠乘波体设计［27］Fig.5 Doble swept waverider design［27］

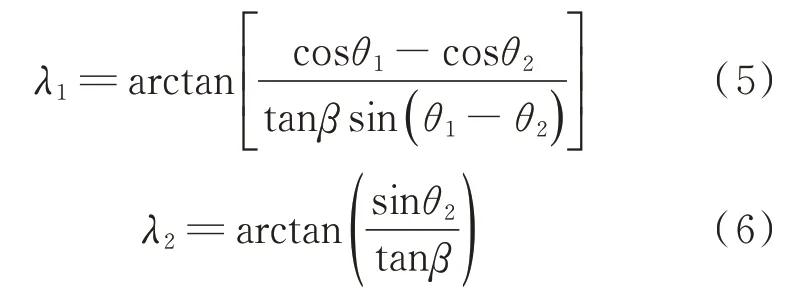
此外，由于第一后掠区域和第二后掠区域之间的斜率变化剧烈，不符合吻切锥理论的ICC 曲线二阶导数连续性要求，刘传振等引进非均匀有理 B 样条（Non-uniform rational B-spline，简称NUBRS）辅助设计ICC 曲线，设计参数和乘波体外形参数之间的数学关系详见文献［27-30］。

总结上述4 种涡升力乘波体的详细设计原理，可见吻切理论的灵活性可有效设计指定前缘型线构型。同时，激波出口型线与前缘线存在特定的数学关系，若要保证前缘线构型的灵活性，要在一定程度上牺牲激波出口型线的设计灵活性，这不利于充分发挥吻切锥乘波体设计方法在构造理想的激波出口型线上的优势。此外，采用NURBS 辅助设计双后掠乘波体，如图6 所示，理论激波出口曲线与实际激波出口曲线存在偏差，影响乘波体下表面气流的横向流动。根据机体/发动机一体化设计观点，这也给机体/发动机一体化设计带来不便。

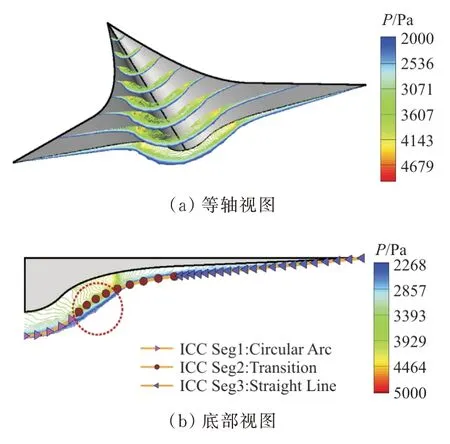
图6 使用NURBS 设计乘波体的流场和设计激波与实际激波对比［30］Fig.6 The flowfield and comparison between design shock and actual result of the design waverider with NURBS［30］

1.2 基于激波装配法的波导体法

陈冰雁等将激波装配法引入乘波体设计，拓宽了乘波体的设计空间，提出波导体（Shock Generating Body，简称SGB）的乘波体设计方法，通过建立波导体与乘波体之间的特定关系，可生成具有特定平面特征的乘波体。与激波捕捉法不同，激波装配法将流场的外激波作为未知边界同流场一起求解，得到流场外激波为精确激波，所得激波面可直接用于乘波体设计，如图7 所示。基于激波装配法的波导体法设计具有双后掠特征的乘波体，如图8 所示。基于激波装配法的波导体法为涡升力乘波体设计提供了一种新的思路，但探究波导体与乘波体外形对应关系规律的过程较为复杂，在涡升力乘波体设计中的应用以及带来的低速气动效益有待进一步研究。

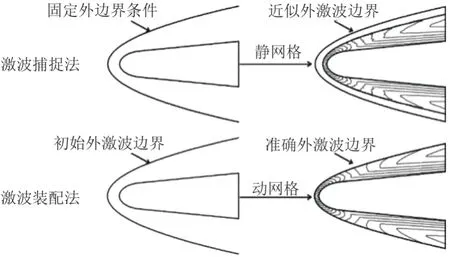
图7 激波捕捉法与激波装配法比较［32］Fig.7 Comparison between shock-capturing method and shock-fitting method［32］

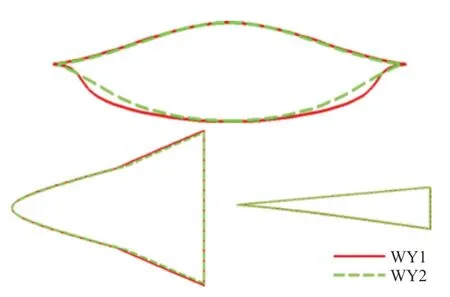
图8 波导体法双后掠乘波体外形［32］Fig.8 Double swept waverider based on SGB method［32］

1.3 基于给定激波面的投影法

针对乘波体前缘型线和激波出口型线的灵活性不能同时兼顾的问题，李永洲等基于给定激波面的投影法指定乘波体前缘线和后缘线，提出一种前后缘型线同时可控的乘波设计。经过气动修型后的乘波体外形如图9 所示，下表面蓝色部分采用流线追踪技术获得，红色部分采用几何重构的方法进行设计，可采用不同的混合函数对下表面修型，是一种“类乘波面”，这对乘波特性造成了一定程度的破坏，靠近激波出口的底部两侧气流存在泄露，升阻比有所降低，且横向流动性不够均匀，不同的混合函数处理下表面对乘波体的影响也较大，该设计方法仍然存在一定的不足。

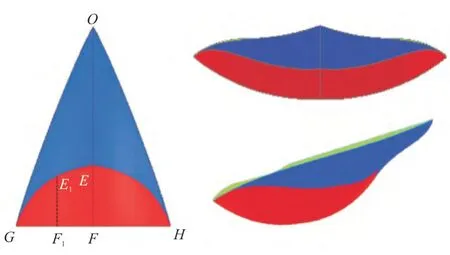
图9 气动修型的三维乘波体构型［33］Fig.9 Three-dimensional configuration of aerodynamic modification waverider［33］

李珺等利用涡升力乘波体定制前缘型线的设计思想，在绕零攻角圆锥型激波流场中基于投影法设计双后掠乘波体前缘线，进一步拓展了双后掠乘波体设计空间。基于投影法的双后掠乘波体设计原理如图10 所示，将乘波体前缘线的平面形状向基准流场的激波面逆向投影可得到乘波体前缘线，然后采用流线追踪技术获得乘波体完整构型。

图10 基于投影法的乘波体设计［35］Fig.10 Waverider design based on projection method［35］

基于给定激波面的投影法下生成具有定后掠角特征前缘和双后掠特征前缘的两种涡升力乘波体如图11 所示。

图11 基于投影法的定后掠角乘波体和双后掠乘波体［35］Fig.11 Constant angle of sweepback waverider and double swept waverider besed on projection method［35］

相较于基于吻切理论的定前缘型线法，基于给定激波面的投影法有效改善双后掠乘波体的激波出口型线偏差问题；同时，乘波前缘平面形状与基准流场之间的设计解耦，一定程度上拓展了涡升力乘波体的设计灵活性。

然而，李珺等以圆锥激波流场作为给定激波面，激波出口型线固定为圆弧型线，尚未解决激波出口型线设计灵活性问题。该方法能有效控制俯视图形状，而较难控制正视图型线。

2 低速“涡升力”

在低速阶段，涡升力乘波体依靠“涡效应”提升飞行性能。宋赋强等设计一种宽速域乘波体，采用了大后掠角的设计，研究表明在低速飞行时，大前缘后掠角引起的漩涡对改善乘波体低速气动性能具有很大的贡献。后掠角

λ

=75°的大后掠角乘波体在低速下（

Ma

=0.3，

H

=1 km）、攻角分别为

α

=0°、

α

=10°和

α

=25°涡量等值面图对比如图12 所示，可以看出：攻角

α

=0°时涡的强度很弱，

α

=10°时涡强度明显增大，

α

=25°时涡在头部的小部分区域保持完整，其他部位开始逐渐破裂，越靠近底部破裂越严重。大后掠角乘波体的低速气动特性随着涡强度增强而提升明显，在

α

=0°时升阻比仅约为 1.5，

α

=20°时达到最大，为 9.737，

α

=25°时由于前缘涡破裂，开始下降约为8.6。

图12 低速（Ma=0.3，H=1 km）不同攻角下乘波体涡量等值面图［24］Fig.12 Section diagram of vorticity at different angles of attack at low speed（Ma=0.3，H=1 km）［24］

Zhao Z T 等为探究尖头乘波体与三角翼乘波体的“涡效应”，研究了

Ma

=1.8、高度

H

=10 km、攻角

α

=10°条件下尖头乘波体和三角翼乘波体的涡结构与升力特性，并与常规吻切锥乘波体做了对比，如图 13 所示。从图 13（a）和图 13（c）对比可以看出：尖头乘波体的前缘涡明显强于常规吻切锥乘波体，更强的涡结构导致更低的上表面前缘附近压力，从而相较于常规乘波体具有更高的升力系数。从图13（b）和图13（c）对比可以看出：三角翼乘波体的前缘涡与常规吻切锥乘波体相差不大，但稍强，所以三角翼乘波体的上表面前缘附近压力稍低于常规乘波体，升力系数稍高于常规乘波体。

图13 三种乘波体低速涡结构和上表面压力对比［26］Fig.13 Comparison of the vortex structure and upper surface pressure of three types of waverider at low speed［26］

刘传振等和李珺等对比双后掠和单后掠乘波体在低速下（

Ma

=0.4，

H

=0 km）的上翼面压力系数

C

的分布。后掠角组合为

λ

=70°、

λ

=50°的双后掠乘波体和

λ

=

λ

=70°的单后掠乘波体对比如图14 所示，可以看出：其在低速阶段的涡效应与传统定后掠角的乘波体相比有稍许不同，但与常规战斗机的“边条翼”类似，即由第一后掠（大后掠角）前缘引起“涡”，之后，该“涡”经第二后掠（小后掠角）前缘扰动而增强，引起前缘线附近背风面的低压区，与定后掠角的乘波体相比，这能进一步增加升力。

图14 双后掠和单后掠乘波体在低速涡结构对比［35］Fig.14 Comparison of vortex structure between double swept and single swept waverider at low speed［35］

同时，刘传振等设计6 种弯头乘波体作为对比（如图15 所示）探究第二后掠角对涡升力的影响，它们的第一后掠角均为

λ

=70°，第二后掠角分别为

λ

=30°、40°、50°、60°、70°，其他设计参数相同，在低速下（

Ma

=0.4，

H

=0 km）的升阻比随攻角变化曲线如图16 所示，可以看出：后掠角组合为

λ

=70°，

λ

=70°，即实际为单后掠的乘波体升阻比最小，约为2.7。双后掠乘波体在低速具有比单后掠更优的气动性能，且随着第二后掠角的减小，升阻比呈增大趋势，以

λ

=70°、

λ

=50°为例，低速下升阻比达3.5。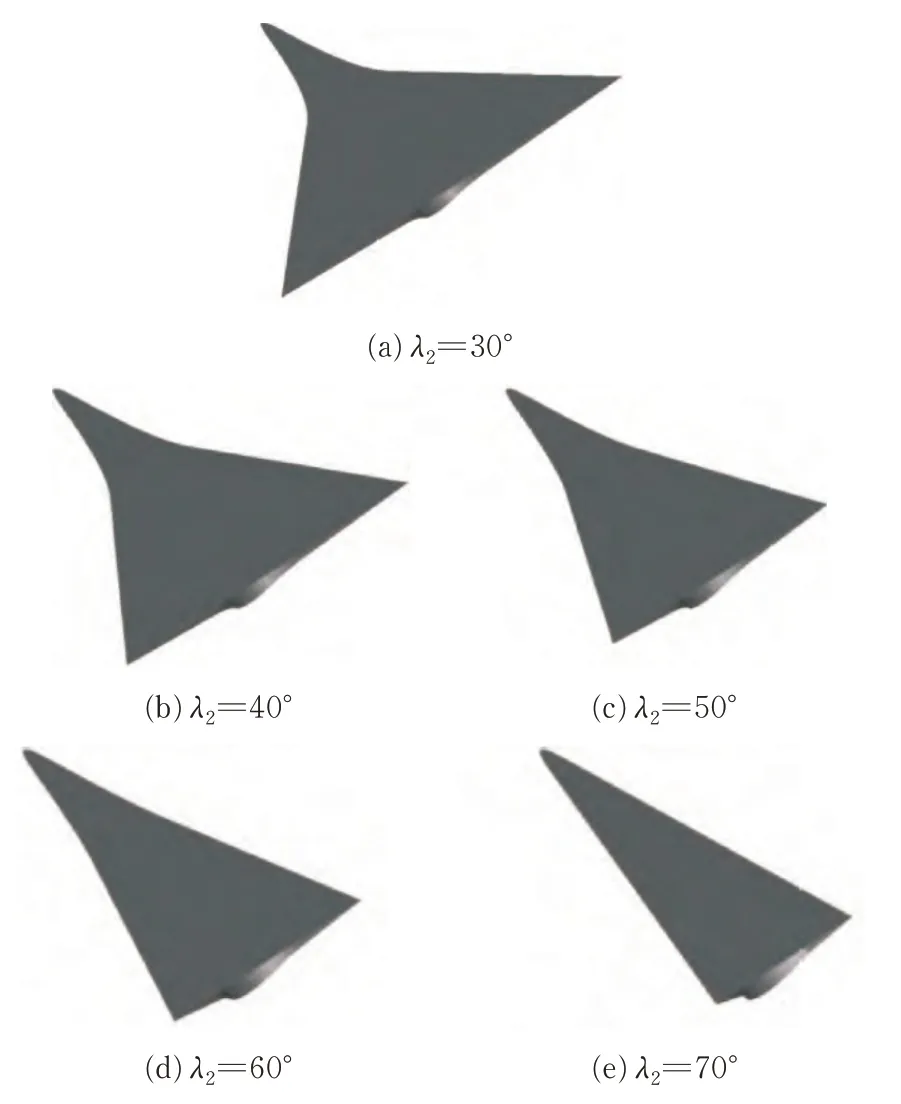

图15 6 种双后掠外形示意图［27］Fig.15 Sketches of 6 types of double swept shapes［27］

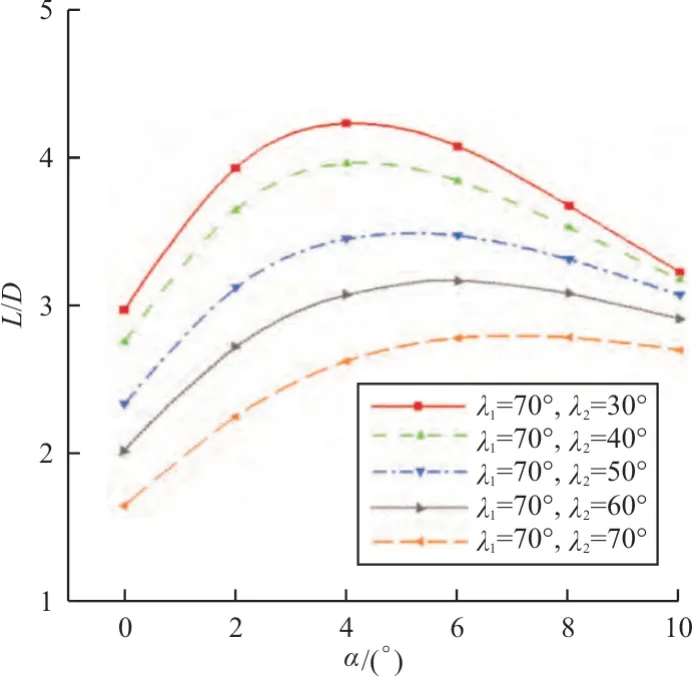
图16 6 种双后掠外形在低速下升阻比对比［27］Fig.16 Comparison of lift to drag of 6 types of double swept shapes at low speed[27]

3 高超声速大攻角非线性

涡升力乘波构型不仅能提高低速的气动性能，在高超声速大攻角时存在非线性升力增量可 进 一 步 提 升 高 超 声 速 气 动 性 能 。涡升力乘波体大攻角非线性升力曲线如图17 所示，可以看出：从4°攻角开始存在一定的大攻角非线性升力增量，随攻角增大，这种非线性增量也随之增大。这种非线性升力在高超声速偏离设计状态下同样存在，随着马赫数的增长，这种非线性升力特性更加明显。

图17 涡升力乘波体大攻角非线性升力曲线［22］Fig.17 Nonlinear lift coefficient of vortex waverider［22］

而针对高速下大攻角非线性升力来源进行的研究，可总结为来源于漩涡和来源于激波的两个不同的观点，下面我们分别综述相关研究。

3.1 来源于漩涡的观点

从 19 世纪 70 年代始，美国 NASA 就对超声速下不同航空器的涡流动展开了实验研究，包括平板、导弹、升力体和机翼等各种飞行器结构，前缘后掠角、前缘钝化程度等几何对涡结构的影响。P.E.Rodi认为，由于后掠角较大，在第一后掠前缘处会生成漩涡，这一漩涡在产生后会沿机身向后发展，并稳定附着在对称面附近的上表面上，而高速大攻角时的额外非线性升力增量则来源于由这一附着漩涡诱导产生的低压区（如图18（a）所示）。随后，刘传振等在定平面形状的乘波体设计时进一步验证了该现象（如图18（b）所示）。段焰辉等和 Zhao Z T 等在提出定后掠角设计（如图19 所示）与尖头乘波体（如图20 所示）时，都分析了设计状态

α

分别为0°～12°时的上表面压力分布变化，可见不同攻角时随着攻角增大，涡效应诱导的上表面低压区逐渐增大，强度也逐渐增强，他们都将此现象与乘波体升力系数的非线性增长联系起来，认为这是造成升力曲线均呈非线性趋势的原因。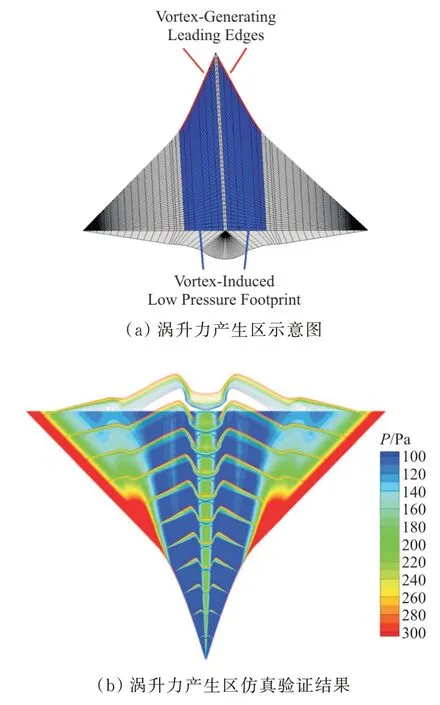

图18 大攻角下乘波体涡升力特征示意图［22，39］Fig.18 A sketch of vortex lift waverider features at high angles of attack［22，39］

图19 定后掠角乘波体设计状态下不同攻角时上表面压力云图［23］Fig.19 The upper surface pressure of waverider with constant swept angles at design state with different angles of attack[23]

图20 尖头乘波体设计状态下不同攻角时上表面压力云图［25］Fig.20 The upper surface pressure of cuspidal waverider at design state with different angles of attack[25]

3.2 来源于激波的观点

刘传振等详细研究了双后掠乘波体上下表面各自对升力的贡献，发现升力的增加主要由下表面贡献，而上表面对升力的贡献很小，因此，他们指出高超声速下的非线性升力来自于漩涡效应存在问题，进一步通过对比实验，研究发现非线性升力与激波附着有关，即“波效应”。

刘传振等将来流分解为沿前缘切向和法向的分量，如图21（a）所示，采用二维斜激波关系式（7）分析激波附着变化趋势，公式（8）分析斜激波前后压强比：

式中：

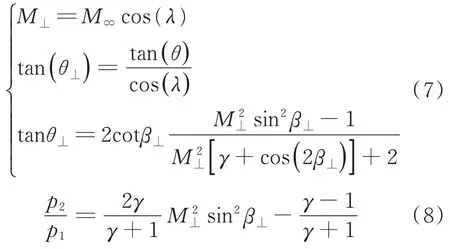
θ

为物面角；

β

为激波角；

λ

为前缘后掠角；

M

为来流马赫数；

γ

为气体常数，“⊥”代表垂直于前缘线的后掠面上的变量。当攻角为

α

时，物面角

θ

=

θ

+

α

，攻角

α

越大，物面角

θ

也越大，如图 21（b）所示。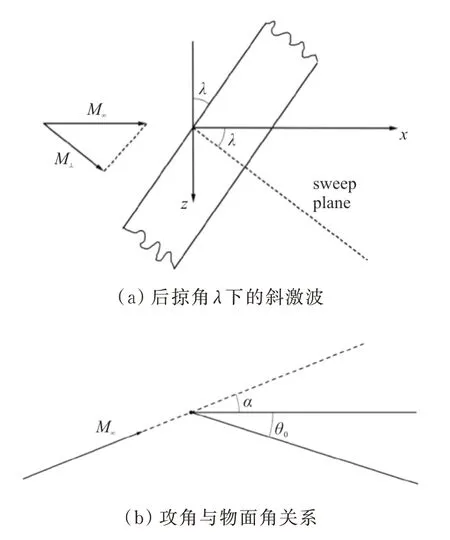

图21 前缘后掠角的激波关系［41］Fig.21 Shock wave relations of sweep leading edge［41］

从式（7）～式（8）可得：到激波前后压强比

p

/p

与物面角

θ

以及前缘后掠角

λ

的关系。根据这一关系，Liu C Z 等计算了几个不同前缘后掠角

λ

下的压强比随物面角变化的关系如图22所示。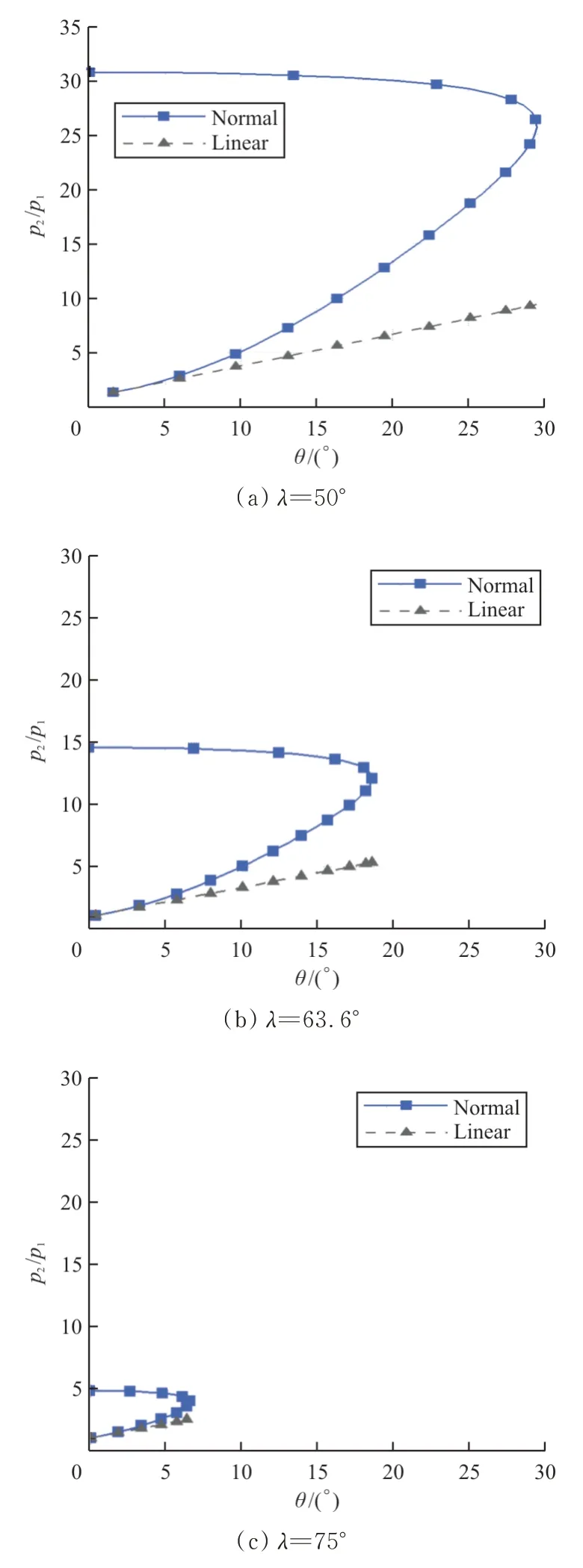

图22 不同后掠角下压强比随物面角变化［41］Fig.22 Pressure ratio via deflection angle at different sweep angles (Ma=8)［41］

从图22 可以看出：

（1）激波脱体前，压强比随物面角明显的非线性增长。由于波后的压力直接作用于双后掠乘波体的下表面，且双后掠乘波体的非线性升力主要由下表面贡献，双后掠乘波体升力系数随攻角非线性增长的原因。

（2）前缘后掠角越小，激波脱体对应的物面角越大，这说明后掠角越小激波越难脱体，同时压力比的非线性增长也越显著，这也解释了观察到的前缘后掠角越小，升力系数的非线性增长越强的现象。

刘传振等计算了四种乘波模型在20°攻角设计状态下（

Ma

=8、

H

=30 km）的流场结构验证上述观点，Model 1 为第一和第二后掠角分别为75°和 50°的双后掠乘波体；Model 2～Moedl 4 均为定后掠角乘波体，Model 2 的后掠角为63.6°，其长度、平面投影面积和容积率与Model 1 相同；Moedl 3和Moedl 4 则是长度与Model 1 相同，后掠角分别为 75°和 50°。在 20°攻角下 Model 1 非线性升力增长率为 23.4%，Model 2 为 15.6%，Model 3 的非线性升力在四者中最小，为6.3%，Model 4 最大，为28.1%。这四种乘波模型横截面压力流场分布如图23 所示，纵截面压力流场分布如图24 所示。可以看出：无论从横截面还是纵截面压力流场分布，均可见Model 1 的第一后掠和Model 3 的前缘激波率先脱体且泄露程度最为严重，然后是Model 2 的前缘激波脱体，最后是Model 1 的第二后掠激波脱体和Model 4 的前缘激波脱体，后掠角与激波脱体先后顺序、严重程度以及非线性升力的大小的关系和之前的讨论相符。

图23 横截面压力分布对比（α=20°）［41］Fig.23 Pressure distribution comparison of cross sections (α=20°)[41]

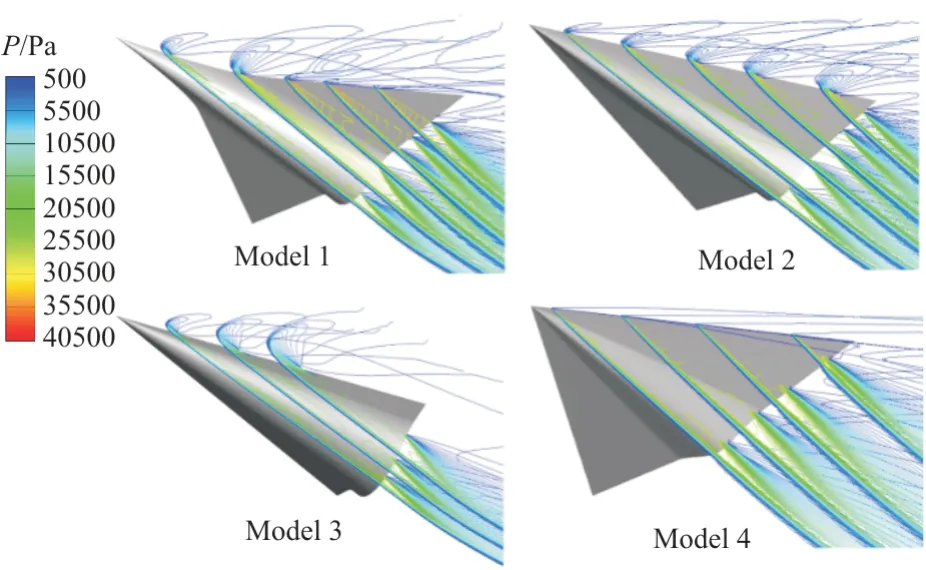
图24 纵截面压力分布对比（α=20°）［41］Fig.24 Pressure distribution comparison of longitudinal sections (α=20°)[41]

4 研究建议

国内外对于乘波体的宽速域问题进行了大量研究，但多为超声速阶段的宽速域，在低速起飞阶段的研究较少。其中涡升力乘波体通过定制前缘构型，利用前缘涡效应提升低速气动性能，研究较为系统，但仍然存在一些不足，有待进一步深入，研究建议有：

（1）基于吻切理论的定前缘型线法的涡升力乘波体设计较为成熟，目前多采用吻切锥基准流场，不足之处在于激波出口型线和前缘线的灵活性不能兼顾。其他更为灵活的流场有可能兼顾涡升力乘波体的激波出口型线和前缘型线的设计灵活性，如吻切流场。

（2）基于给定激波面的投影法可将前缘线和激波出口型线解耦设计，目前人们研究了以圆锥流场对涡升力乘波体的宽速域气动性能，但激波出口型线灵活性问题仍未解决。涡升力乘波体的激波出口型线灵活性可作为下一步的研究方向。

（3）基于激波装配法的波导体法可精确设计激波流场，是一种有效的涡升力乘波体设计方法。波导体与乘波体之间的几何关系尚处于初步研究阶段，如何通过是基于激波装配法的波导体法设计特定前缘型线的涡升力乘波体，其中的关系有待进一步明确。

5 结束语

涡升力乘波体在保持了高超声速高升阻比特性的同时，通过定制乘波体前缘型线，在低速诱导前缘涡提升了低速气动性能，因而可以作为宽速域空天飞行器外形的备选设计方案。目前，定后掠角乘波体、尖头乘波体、三角翼乘波体和双后掠乘波体是四种常见的涡升力乘波体。此外，研究表明涡升力乘波体在高速大攻角下还具有有一定的非线性升力，这进一步提升了其高超声速时的气动性能，而对该非线性升力的来源，目前有来源于漩涡和来源于激波两种观点。

本文将涡升力乘波体设计方法归纳为基于吻切理论的定前缘型线法、基于激波装配法的波导体法和基于给定激波面的投影法三大类，分析了三种设计方法的优点和不足，并进一步指明了下一步的研究方向，希望能为涡升力乘波体的进一步发展提供具有价值的参考。