带连续变弯度后缘操纵面机翼的动态失速减缓

欧阳炎 ，寇西平 ，，郭洪涛 ，杨智春

（1.西北工业大学结构动力学与控制研究所，西安710072）

（2.中国空气动力研究与发展中心高速空气动力研究所，绵阳621000）

0 引 言

动态失速是包含一系列流动分离、失速延迟的非定常流动现象，通常在翼型攻角大幅超过静态失速攻角范围，且随时间周期性变化或者急剧增大的情况下发生。发生动态失速时，翼型表面动态失速涡的发展和运动将使翼型的气动力系数极值显著超过定常流动时的情况。机翼可能出现升力骤降、阻力激增、结构振动幅值增大甚至诱发失速颤振，严重影响飞行安全，因此关于动态失速的研究一直是航空领域关注的热点。直升机桨叶翼型负的俯仰力矩（低头力矩）极值决定了桨叶根部变距拉杆的结构强度设计要求，减小动态失速时翼型负的俯仰力矩系数极值对于直升机桨叶而言意义重大。

发生动态失速时的脱体涡通常起源于翼型前缘，因此各种前缘装置最早被用来减缓动态失速。典型的研究工作包括：改变前缘半径和厚度，采用变弯度前缘操纵面、前缘缝翼、微型扰流片以及前后缘联合射流。由于直升机桨叶翼型前缘通常会面临复杂的流动情况，且前缘的变化通常会引起较大的翼型重心位置移动，故前缘控制方法在桨叶上应用比较困难。桨叶后缘部分通常结构相对简单且有较大的操作空间，采用后缘控制的方法逐渐受到研究者们的青睐。

D.Feszty 等利用离散涡方法研究了刚性后缘操纵面减缓翼型动态失速特性，发现正弦脉冲偏转信号能有效减小低头力矩系数的极值；R.B.Green 等在风洞实验中验证了 D.Feszty 等的结论，并提出了一种稍加改进的偏转控制信号；P.Gerontakos 等开展了一系列风洞实验，提出一种类似梯形波的偏转方案，同样取得了很好的控制效果。国内，马奕扬等利用CFD 方法，分析了正弦偏转信号中频率和相位对动态失速减缓效果的影响；王荣等利用沿展向分布的三个操纵面减小了桨毂的振动载荷；刘洋等发现操纵面和主翼之间的缝隙大于弦长的6%时，刚性后缘操纵面偏转时的前缘突起会降低减缓效果。

从上述文献可以看出，人们在利用刚性后缘操纵面减缓动态失速方面进行了较为深入的研究，而采用连续变弯度后缘操纵面进行动态失速减缓的研究比较少见。刚性操纵面在偏转后，中弧线仍是直线形状，而连续变弯度后缘操纵面在偏转后中弧线呈曲线形状。操纵面弯度的连续变化是变体机翼分类中的沿弦向变体。

杨智春等在研究机翼的定常气动特性时发现，和刚性操纵面相比，连续变弯度后缘操纵面在增加升力的同时会带来更大的低头力矩；吴优等计算了翼型攻角大幅度俯仰振荡时的非定常气动特性，发现连续变弯度后缘操纵面能显著提升翼型的升力并降低阻力；Zhuang C 等利用连续变弯度后缘操纵面提高风力机叶片在一个运动周期内的平均升力并减小阻力。由此可知，连续变弯度后缘操纵面在减缓翼型动态失速方面有极大的应用潜力，有必要开展深入的研究。

在已有的研究工作中，不管是采用前缘操纵面还是后缘操纵面，都很少考虑驱动操纵面偏转所需的能量输入。由于驱动系统设计是变体机翼的关键技术之一，本文将连续变弯度操纵面的能量输入需求作为重要的性能指标进行考虑。采用CFD 的方法，研究利用连续后缘操纵面减缓翼型动态失速的可行性；通过与传统刚性操纵面对比，分析后缘操纵面的弯度构型对动态失速减缓效果的影响；从减缓效果和能量输入需求两个方面，得到最佳的连续变弯度后缘操纵面构型。

1 连续变弯度操纵面的定义

等效偏转角定义如图1 所示，传统刚性操纵面（实线）偏转时，将绕着铰链转轴（

x

，0）点作刚体旋转运动，旋转角度

β

即为操纵面的偏转角度。连续变弯度操纵面（虚线）没有一个所谓的转轴点。为了定量描述连续变弯度操纵面的偏转程度，基于翼型后缘点的垂直位移，定义一个等效偏转角，该角度与具有同样弦长和后缘点位移的刚性操纵面偏转角相等。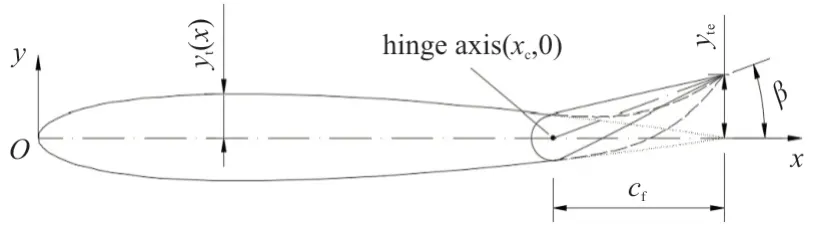

图1 等效偏转角定义Fig.1 Definition of equivalent deflection angle

图1 中，弦长为

c

的刚性操纵面向上偏转时后缘点的垂直位移为

y

，则连续变弯度操纵面的等效偏转角为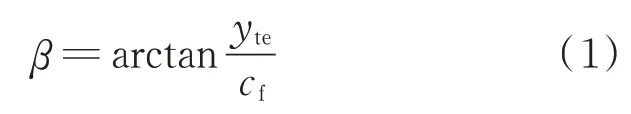

即图中的两种操纵面具有相同的偏转角。

采用式（2）来统一描述后缘操纵面偏转后的中弧线：

式中：

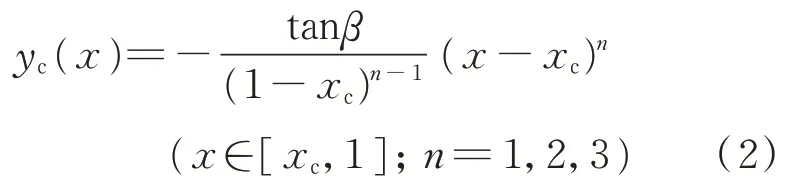
n

为多项式的阶数，决定了操纵面的类型。当

n

=1 时，为刚性操纵面；当

n

等于 2 或 3 时，为连续变弯度操纵面。本文以多项式的阶数来代称连续变弯度操纵面，如2 阶操纵面指的是

n

=2 时的连续变弯度操纵面，以便于理解和计算。单位弦长的NACA 四位数翼型的厚度分布函数

y

（

x

）定义如下：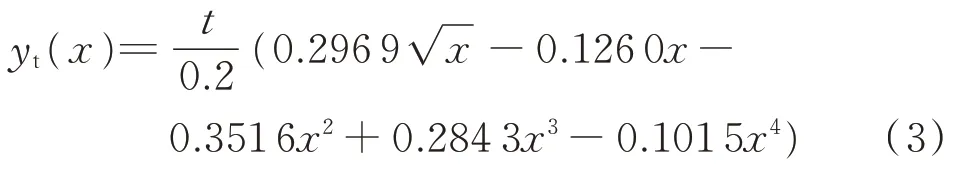

式中：

t

为翼型的无量纲最大厚度（如

t

=0.12 时即是NACA 0012）；

x

∈［0，1］为无量纲弦向位置。假定操纵面在偏转前后的厚度分布保持不变，那么操纵面上翼面（

x

，

y

）和下翼面（

x

，

y

）的位置坐标可按式（4）计算：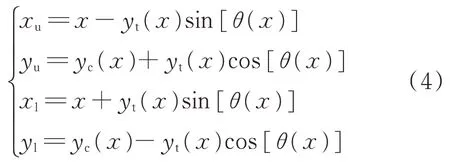

式中：

θ

（

x

）为中弧线函数的斜率。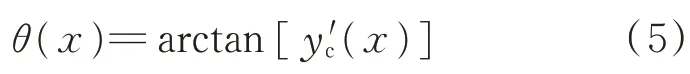

当操纵面弯度多项式的阶数

n

和偏转角

β

确定后，根据式（2）～式（4）便可计算整个翼型上下翼面的坐标。NACA 0012 干净翼型和三种后缘操纵面构型如图2 所示，根据等效偏转角的定义，图2（b）～图2（d）中三种后缘操纵面的偏转角相等。刚性操纵面偏转后，上下翼面在转轴位置处有明显的转折点，而两种连续变弯度操纵面的翼型表面能始终保持光滑连续，且3 阶操纵面比2 阶操纵面弯度的曲率大。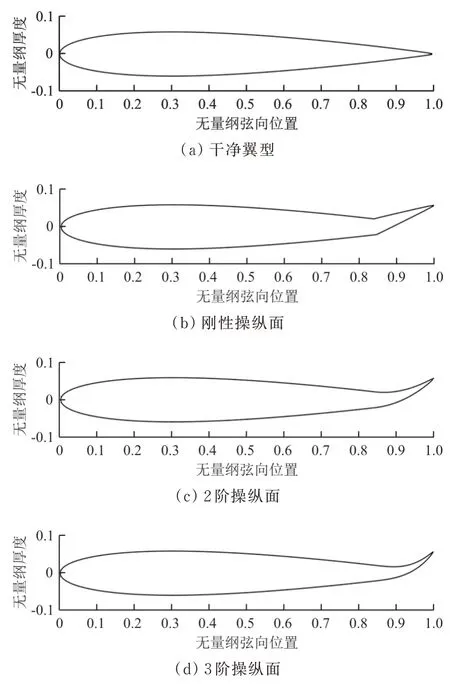

图2 NACA 0012 干净翼型和三种后缘操纵面构型（β=20°）Fig.2 Baseline NACA 0012 and airfoils with different kinds of flap（β=20°）

在工程实际中，刚性操纵面和主翼之间会留有缝隙，即蒙皮在转轴处不连续。因为本文主要关注操纵面弯度的影响，所以在计算过程中假定刚性操纵面在偏转后蒙皮仍保持连续。作动机构驱动刚性操纵面在气流中偏转时，需要平衡操纵面所承受的气动载荷，刚性操纵面的铰链力矩可以作为衡量驱动能量输入的指标。对于连续变弯度操纵面而言，没有所谓的转动轴。为了进行对比分析，在计算过程中将连续变弯度操纵面上的气动载荷对操纵面偏转起始点进行积分求力矩，并仍称之为铰链力矩，以方便叙述。

2 数值计算方法

2.1 控制方程和求解器

为了模拟非定常流动中的分离和动态失速涡，采用基于雷诺平均的N-S 方程作为流场的控制方程：

式中：

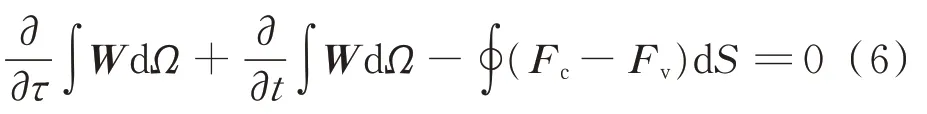
W

=［

ρ

，

ρv

，

ρv，e

］，为守恒变量向量，其中，

ρ

为空气密度，

v

和

v

分别为速度沿

x

轴和

y

轴的分量，

e

为总能量；

τ

和

t

分别为伪时间和物理时间；

Ω

为流场单元体积；

S

为流场单元边界；

F

和

F

分别为对流通量项和黏性通量项。在求解N-S 方程模拟动态失速的大攻角非定常瞬态流动时，需选择合适的湍流模型以保证计算结果的精度。J.A.Ekaterinaris 等对早期的动态失速模拟中的数值方法进行了详细总结。在已有的各种湍流模型中，SST

k-ω

模型使用比较广泛，在预测失速攻角和计算气动力方面都有较好的计算精度和效率。本文在商业软件Fluent中，利用压力基求解器结合SST

k

-

ω

湍流模型求解方程（6），计算翼型动态失速过程中的气动力和流场特性。

2.2 动网格

在翼型俯仰振荡和后缘操纵面的主动偏转过程中，翼型表面的边界位置会按指定规律运动。在Fluent 软件中，可以采用动网格技术来模拟翼型边界的运动。由于不涉及结构的弹性变形，本文计算过程中的主翼和操纵面的运动直接由自定义函数（UDF）给定。采用扩散光顺算法，尽量让远场的网格产生变形，保留翼型近壁面区域的网格形态，确保网格更新后无量纲壁面距离

y

满足要求。当后缘操纵面偏转角

β

=20°时，网格动态更新后的结果如图3 所示，可以看出：变形后的网格质量保持良好。

图3 NACA 0012 干净翼型和带不同操纵面构型网格动态变化结果Fig.3 Dynamic grid deformation for NACA 0012 airfoil and three kinds of flaps

2.3 数值算例

采用与文献［11］相同的翼型和流动工况，将本文CFD 计算结果与文献［11］中的风洞实验数据进行对比，以验证N-S 方程求解器和动网格的计算结果精度。不带操纵面的NACA 0012 干净翼型以减缩频率

k

=0.173 绕四分之一弦长点进行俯仰振荡，来流马赫数

Ma

=0.117，雷诺数

Re

=1.463 296×10。攻角随时间的变化规律为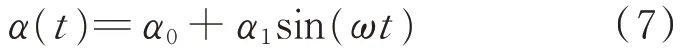

式中：平均攻角

α

=15°；攻角振荡幅值

α

=10°。无量纲角频率

ω

为

式中：

v

为来流速度；

b

为 0.5 倍弦长。流场计算所用C 型网格如图4 所示。通过设置来流方向，使得当翼型水平放置时，攻角

α

=15°。对翼型近壁面网格进行加密处理，通过设置第一层网格高度确保无量纲壁面距离满足

y

≈1.0。利用由疏到密的三套网格（G1、G2 和 G3）进行网格收敛性验证，三套网格包含的单元数目分别为50 160、75 400 和100 800。计算得到的气动力系数随攻角的变化曲线如图5 所示，图中的箭头为时间推进方向。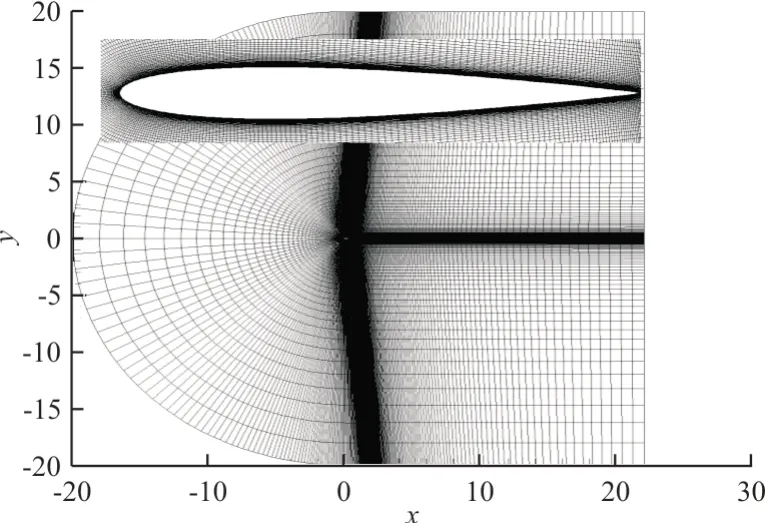

图4 远场网格以及翼型局部放大图Fig.4 The C-type mesh and zoomed view of the NACA 0012 airfoil

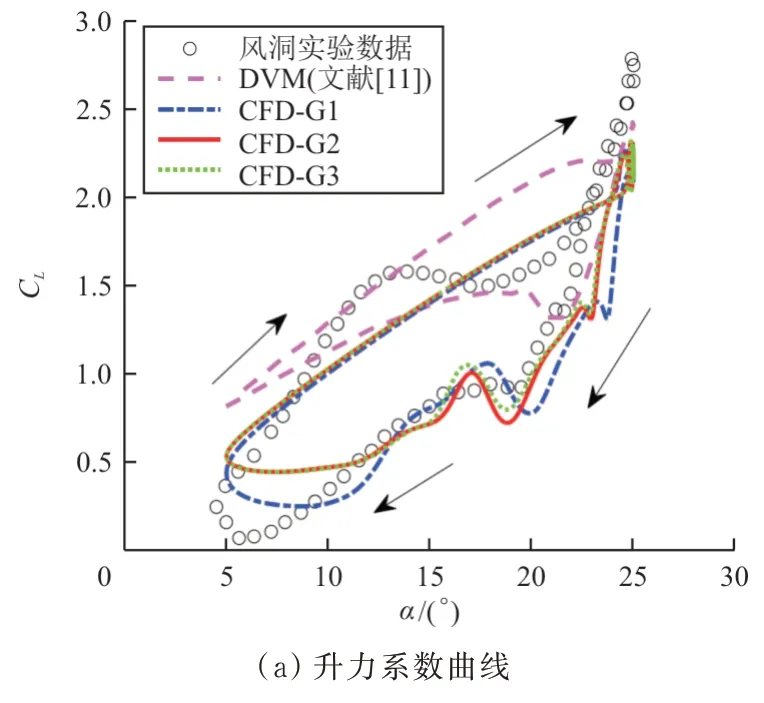
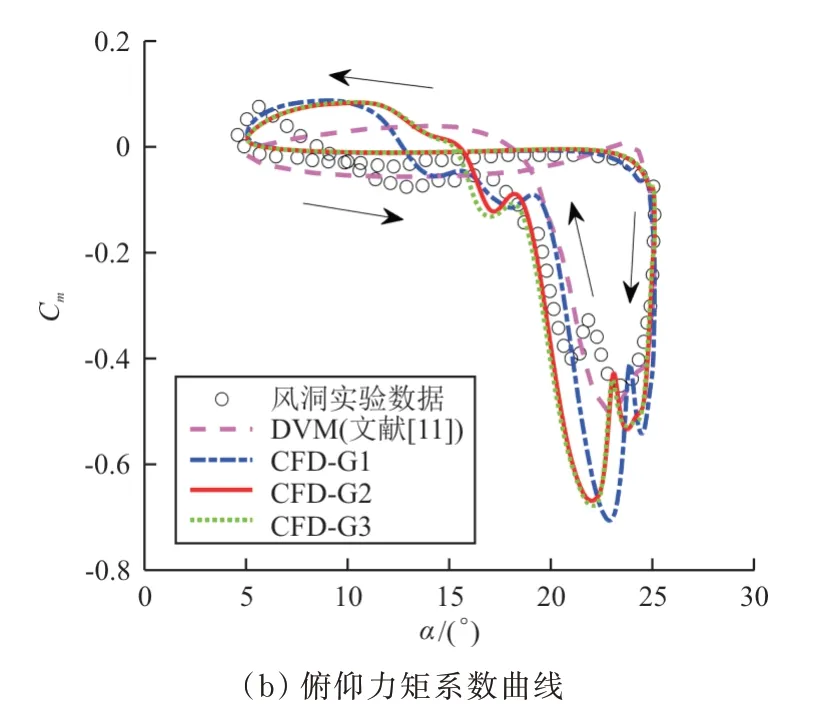
图5 干净翼型俯仰振荡时气动力系数时滞曲线Fig.5 Aerodynamics loops for oscillating

从图5 可以看出：中等网格G2 和加密网格G3的计算结果非常接近，在后续的计算中采用G2 网格即可兼顾计算精度和效率；对于升力系数曲线，本文的计算结果和实验结果吻合较好；对于力矩系数曲线，在翼型攻角上行阶段，本文的仿真结果与实验结果吻合较好，在攻角下行阶段则略有差别。E. Guilmineau 等也阐述了同样的差别，并指出可能是因为CFD 方法过高地估计了动态失速涡脱落造成的吸力。

无量纲的气动阻尼系数作为指标来衡量翼型在一个俯仰振荡周期内从气流中吸收的总能量，由俯仰力矩系数对攻角进行封闭曲线积分计算得到：

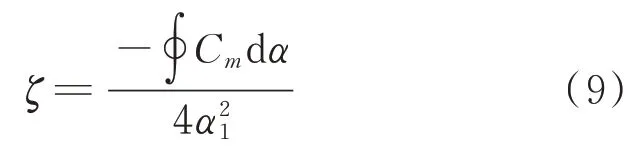
则在图5（b）俯仰力矩系数曲线中，左侧逆时针方向的小闭环意味着正的气动阻尼，右侧顺时针方向的小闭环则对应负的气动阻尼。如果保持俯仰力矩系数曲线的基本形状不变，减小负的俯仰力矩系数极值，也可能会减小顺时针小闭环围成的面积，进而减小整个运动周期的负气动阻尼。

3 操纵面偏转策略

利用占机翼总弦长16%的刚性后缘操纵面，按照正弦脉冲信号向上偏转，可以有效地减小动态失速时的负俯仰力矩系数极值。该脉冲信号的表达式为

由式（10）确定的偏转规律如图6 所示，可以看出：操纵面的偏转规律取决于三个参数：偏转角幅值

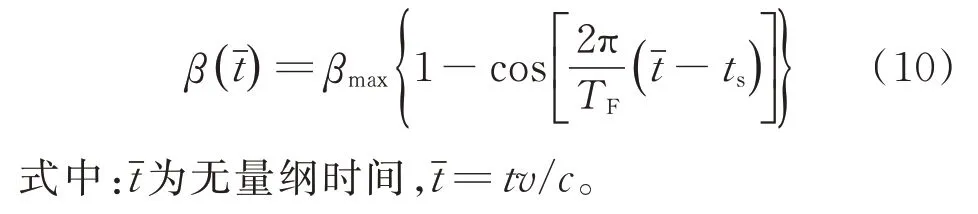
β

、偏转起始时刻

t

以及持续时间

T

。

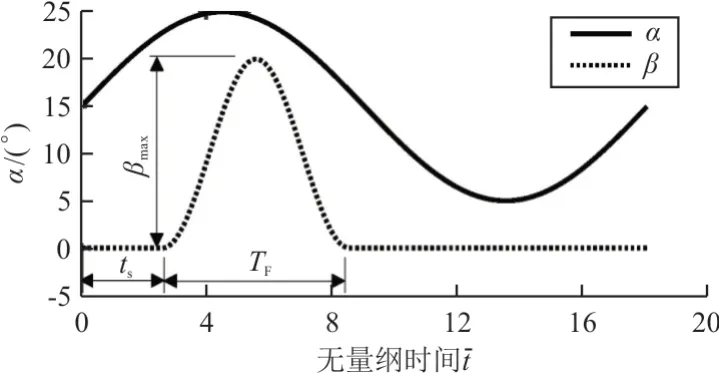
图6 正弦脉冲式偏转信号Fig.6 Pulse deflection signal profile

文献［11］通过一系列的变参分析，在保持升力特性和减缓动态失速两方面进行了综合考虑，得出了最优控制规律的系数为：

β

=20°，

t

=2.2，

T

=6。本文采用与此相同的偏转控制规律，对比研究不同类型操纵面减缓动态失速的效果。

4 结果与讨论

4.1 动态失速减缓时的气动力系数分析

采用上一节中描述的控制规律进行动态失速减缓后，带不同后缘操纵面翼型的气动力系数如图7 所示。为了加深对动态失速特性的理解，图中也加入了干净翼型的定常气动力系数曲线。

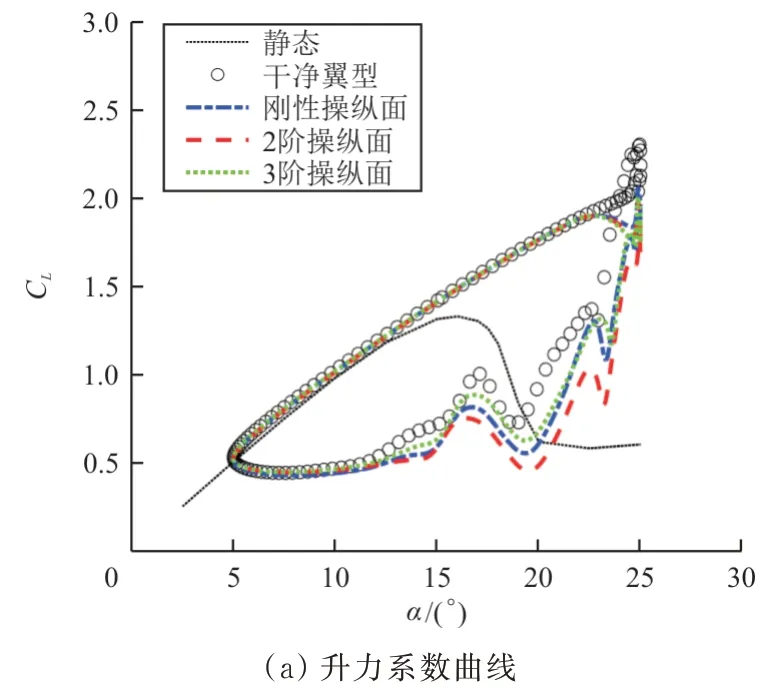
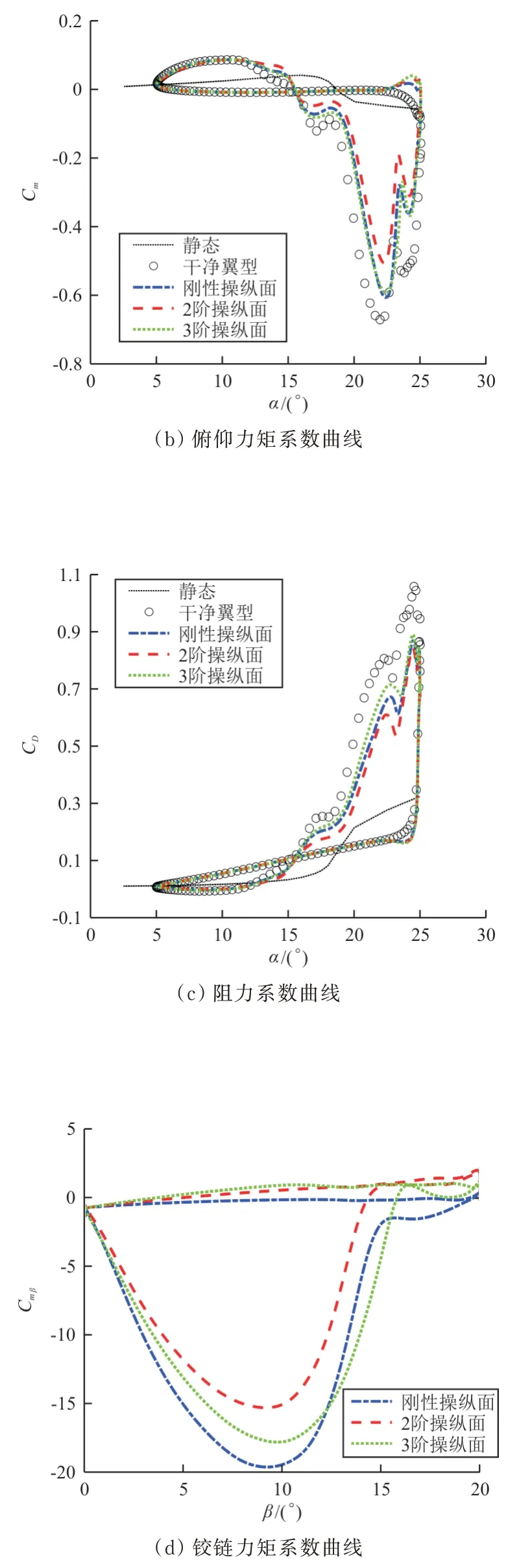
图7 不同类型操纵面动态失速减缓效果Fig.7 Comparison of dynamics stall control by different kinds of flaps

从图7（a）可以看出：对于干净翼型而言，当

α

= 16.00°时将发生静态失速，而发生动态失速时，升力失速则被显著推迟到更大的攻角下，这是动态失速的一个典型特征。在翼型攻角上行的初始阶段，操纵面还没有开始偏转，升力系数随着攻角的增大而线性增大。当

α

= 24.96°↑时（↑和↓分别代表上行和下行方向），干净翼型的升力系数达到最大，此时的升力系数比定常条件下的最大升力系数值大73.4%。当

α

=21.90°↑时，操纵面开始向上偏转。三个带操纵面翼型的升力系数先减小后增大，升力系数极值小于干净翼型的情况。在攻角下行的大部分阶段，操纵面偏转将造成不同程度的升力损失。好在这种升力损失对于直升机桨叶翼型而言并非致命缺陷，因为在高速飞行时，桨叶产生的升力大部分源自外侧65%～85%展向位置区域。

从图7（b）可以看出：相对于干净翼型而言，后缘操纵面的偏转显著减小了负的俯仰力矩系数的极值。3 阶操纵面和刚性操纵面的减缓效果非常接近，2 阶操纵面的减缓效果最好，能将俯仰力矩负的极值进一步减小。操纵面偏转之后，右侧顺时针的小闭环曲线的面积也明显减小，对于实际的直升机桨叶结构而言，这意味着从气流中吸收的能量有所减少，降低了桨叶发生失速颤振的风险，有利于减小结构的振动幅值。

尽管阻力特性不是本文的研究重点，但是从图7（c）可以看出：后缘操纵面偏转后，翼型的阻力相对于干净翼型有不同程度的下降，且最大阻力系数下降明显。这说明使用后缘操纵面进行动态失速减缓时，不会造成阻力增大。

从图7（d）可以看出：在三种操纵面上行偏转阶段，铰链力矩系数很小且变化缓慢。在下行偏转阶段，当偏转角小于15.00°↓之后，铰链力矩系数值迅速减小，即作动机构需要提供越来越大的作动力才能让操纵面按照信号指令偏转。当偏转角小于10.00°↓之后，铰链力矩系数将达到极值。

综上所述，在相同的偏转策略下，驱动2 阶操纵面的能量需求是最小的。

尽管文献［11］中的偏转规律仅对刚性后缘操纵面而言是最优的，但连续变弯度操纵面在相同的偏转规律下表现出了更好的减缓效果。可以预见，如果采用合适的优化算法得到连续变弯度操纵面的最优偏转规律，那么利用连续变弯度后缘操纵面进行动态失速减缓的效果将会有更进一步的提升。

图7 中涉及的气动力系数极值以及按照公式（9）计算得到的一个运动周期内的气动阻尼系数如表1 所示。

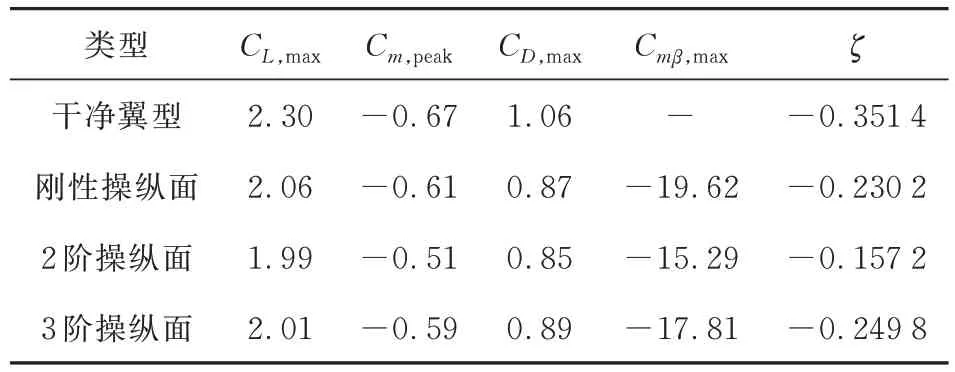
表1 带不同类型操纵面翼型的关键性能参数Table 1 Key parameters of different kinds of flaps

从表1 可以看出：三种操纵面偏转造成的升力损失基本处于同一水平；与干净翼型相比，刚性操纵面和3 阶操纵面可将负的俯仰力矩系数极值分别减小8.96%和11.94%，而2 阶操纵面的减小量达到23.88%，减缓效果最为明显；操纵面偏转后，翼型的最大阻力至少会下降16.04%；在偏转过程中，连续变弯度操纵面所承受的气动载荷要小于刚性操纵面的情况，这对连续变弯度操纵面尤其是2 阶操纵面的内部结构设计而言是一个潜在的优势；刚性操纵面、2 阶和3 阶操纵面偏转后，翼型的负气动阻尼将分别减少34.49%、55.26% 和28.91%。综上所述，利用2 阶操纵面减缓翼型动态失速的效果最好。

4.2 动态失速减缓时的流场分析

为了分析翼型发生动态失速时的流场细节，研究后缘操纵面偏转减缓动态失速的机理，通过流场的压力系数云图和流线图来追踪动态失速发生前后的一系列非定常流动现象。一些典型时刻的流场结果如图8 所示，在每一时刻，首先关注干净翼型的流场，然后分析后缘操纵面偏转造成的影响，对比操纵面弯度产生的差异。

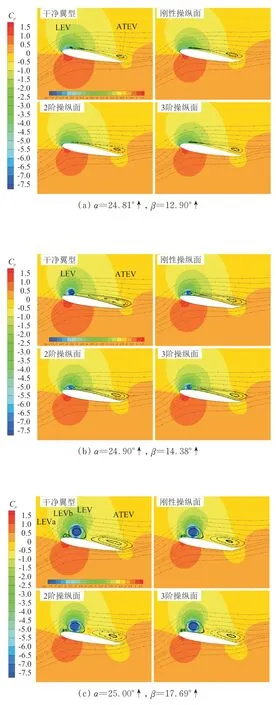
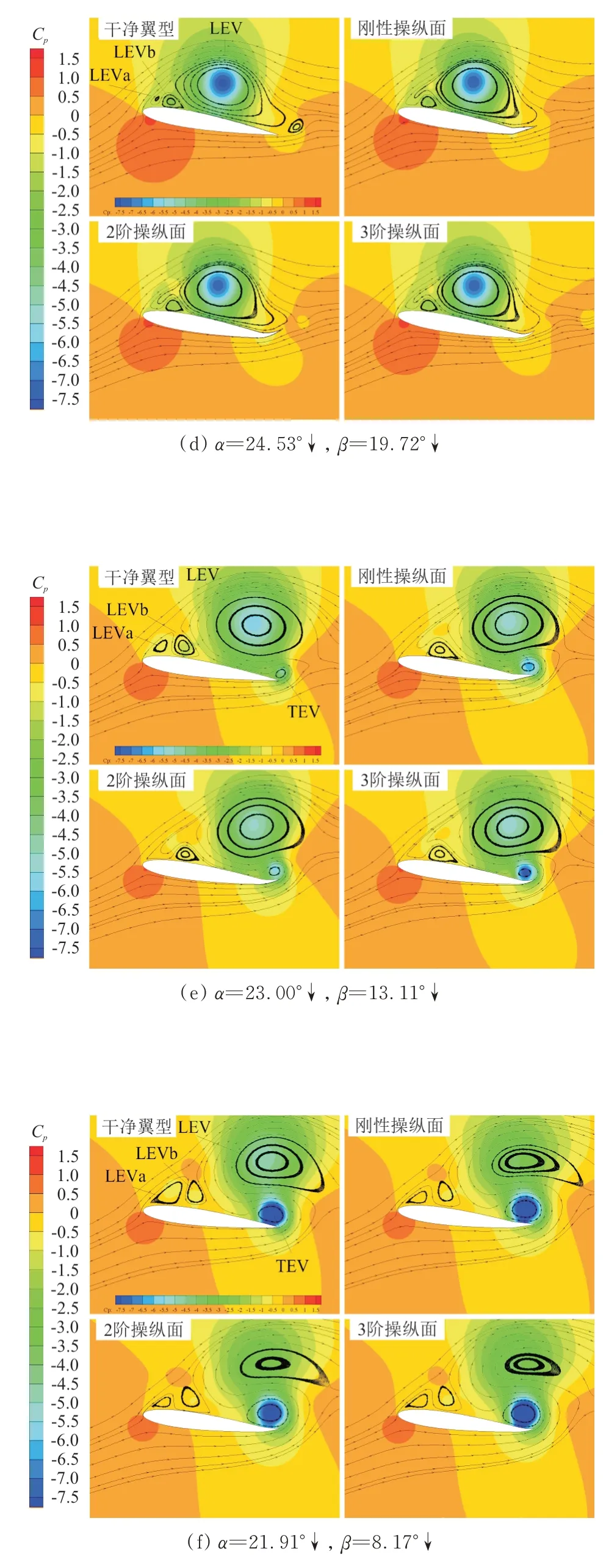
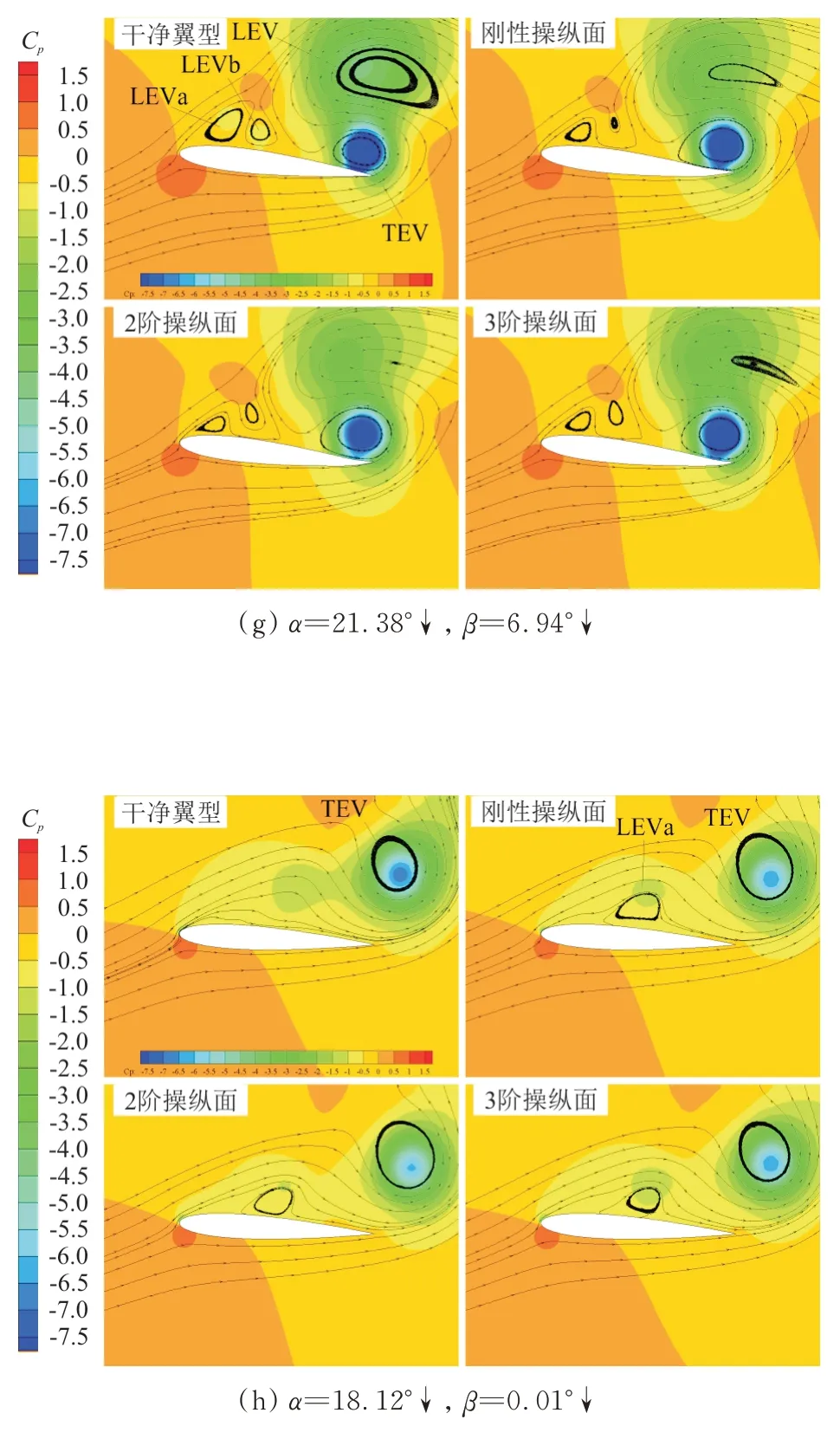
图8 典型时刻的压力系数云图和流场图Fig.8 Typical instantaneous Cp counter and streamlines

当攻角增大超过静态失速攻角（16.00°）之后，翼型上表面的流动仍将保持完全附着。从图8（a）可以看出：到

α

=24.81°↑时刻，各个翼型的后缘上翼面都出现了大面积的封闭回流区域，形成了一个稳定的后缘附着涡（Attached Trailing-edge Vortex，简称ATEV）；干净翼型的上翼面同时还出现了前缘涡（Leading-edge Vortex，简称LEV），干净翼型进入动态失速阶段；后缘操纵面向上偏转了12.90°时，三个带操纵面翼型的上表面只有后缘附着涡。可见，向上偏转后缘操纵面将推迟前缘涡的产生。

随着后缘附着涡的增强，对翼型表面的压力分布会产生更大的影响，干净翼型的俯仰力矩系数也会偏离先前变化缓慢的趋势而迅速趋向负的极值，俯仰力矩发生失速。当攻角由24.71°↑增至24.96°↑时，干净翼型的升力线斜率增大。从图8（b）可以看出：此时升力的增大是后缘附着涡和前缘涡共同作用的结果，三个带后缘操纵面机翼的上翼面也都出现了前缘涡，只是不如干净翼型上的前缘涡发展得充分。

图8（c）是攻角上行到最大值时刻的流场情况，可以看出：和上一时刻相比，前缘涡开始往下游移动。当后缘附着涡和前缘涡的区域持续增大时，在前缘涡的上游位置出现了一对反向旋转的小涡（LEVa 和LEVb）。由于这对小涡与先前生成的后缘附着涡和前缘涡相比，在尺寸和强度上要小很多，通常被称为次级涡，文献［30-31］中也描述了类似的流动现象。

在翼型攻角下行的初始阶段，前缘涡继续向下游移动且区域逐渐增大，而后缘附着涡的区域将逐渐缩小，最终被前缘涡合并。在经历一段短暂的振荡之后，干净翼型的升力系数在

α

=24.53°↓时达到第二个峰值点（

C

=2.25），随后急剧下降，升力发生失速。从图8（d）可以看出：前缘涡已将后缘附着涡吸收，并移动至弦长中点位置。干净翼型后缘的下游区域出现一个小涡，随后立即消失。三个带操纵面翼型的流场结构基本相似，上翼面只有前缘涡和一个靠下游的次级涡，先前靠上游的次级涡已被前缘涡合并吸收。

从图8（e）可以看出：干净翼型上翼面一共有四个涡结构，后缘涡（Trailing-edge Vortex，简称TEV）已经出现。由于前缘涡已经开始从翼面分离，后缘上翼面已有足够的空间，使得下翼面的气流能以平滑的方式调头回流到达上翼面。后缘涡最早出现在刚性操纵面上，但此时3 阶操纵面上后缘涡核区域的压力系数更低，说明发展得更为迅速。

干净翼型的俯仰力矩系数在攻角下行至

α

=21.91°时达到负的极值。从图8（f）可以看出：前缘涡已经从干净翼型上翼面完全脱离，此时位于后缘涡的正上方。这两个涡核的低压区域将整个翼型的压心移到了靠近后缘的位置，由此产生一个极大的低头力矩。后缘操纵面偏转后，翼型的俯仰力矩系数已在稍早的时刻达到负的极值点，此时前缘涡的分离发展得更为充分。

从图 8（a）～图 8（f）可以看出：在翼型的动态失速过程中，前缘涡在发展和分离的过程中会直接与其上下游的其他涡发生相互作用。从图8（g）可以看出：前缘涡已越过干净翼型的后缘点，并向尾流中移动；在三个带操纵面翼型的流场中，前缘涡的环形流动区域变得十分扁平，表明操纵面的偏转加速了前缘涡的发展，尤其在2 阶操纵面的流场中，前缘涡已几近消失。

从图8（h）可以看出：随着攻角继续下行减小，干净翼型上的次级涡会演化消失，后缘涡从后缘上翼面脱落并进入尾流中；在三个带操纵面翼型的流场中，次级涡继续向下游移动并最终从翼面分离，而后缘涡在尾流中发展得更加迅速。

由于流场的滞后效应，直到

α

=9.86°↓时，操纵面偏转对流场的影响才完全消失，即四个翼型的流场形态基本相同。此时，从翼型前缘开始，上翼面的气流在约50%弦长的范围内恢复了附着。

综上，在翼型发生动态失速时，向上偏转后缘操纵面可以推迟前缘涡的生成，加速前缘涡的发展；对后缘涡而言，能加快其生成，而对其演化消失影响不大。

后缘操纵面减缓动态失速的机理可以通过翼型表面的压力分布进一步揭示，如图9 所示。

从图 9（a）可以看出：在图 8（e）时刻，后缘涡在三个带操纵面翼型上发展得更为充分，因此干净翼型的压力系数曲线峰值是最低的。从图9（b）可以看出：在图8（f）时刻，后缘操纵面偏转显著降低了翼型后缘的压力分布峰值，进而减小了翼型的低头力矩。其中，2 阶操纵面对应的峰值最低，因此减缓效果最好。

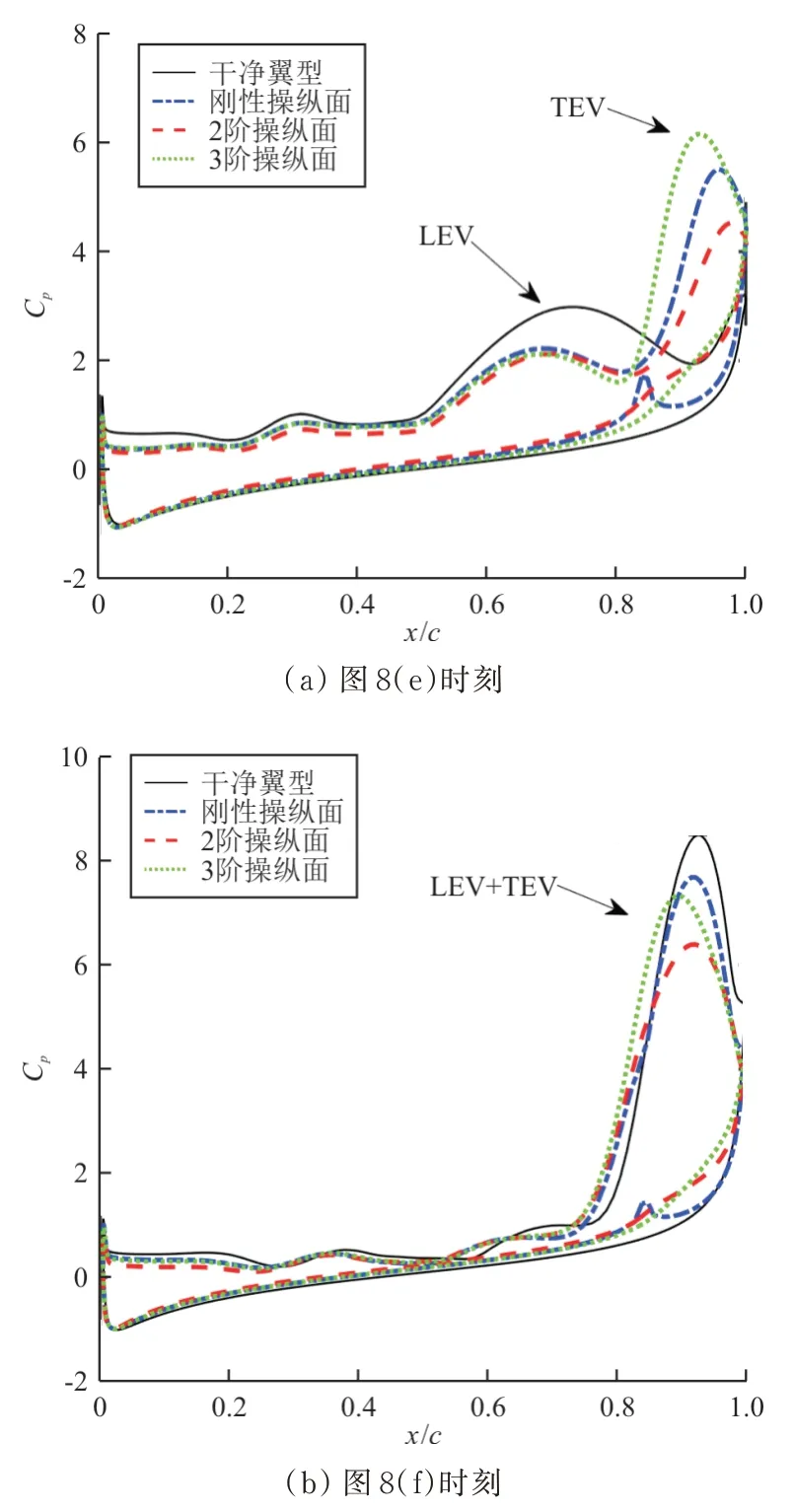
图9 翼型表面压力系数曲线Fig.9 Pressure distribution on different airfoils

5 结 论

（1）当采用相同的正弦脉冲偏转信号时，连续变弯度操纵面能使翼型后缘的压力分布下降更多，因此对动态失速的减缓效果优于刚性操纵面。

（2）在减小俯仰力矩负的极值和减小一个运动周期的负气动阻尼方面，2 阶后缘操纵面的动态失速减缓效果最好。

（3）相比于刚性操纵面和3 阶后缘操纵面，2阶后缘操纵面在一个偏转周期内的铰链力矩系数极值最小，因此需要的驱动能量输入也最小。