机载拖曳体动力学建模及分析

张戈 ，刘南 ，侯良学 ，杨希明

（1.航空工业空气动力研究院气动研究与试验二部，沈阳110034）

（2.高速高雷诺数气动力航空科技重点实验室，沈阳110034）

0 引 言

机载拖曳体系统在航空领域有着较多的应用，机载甚低频拖曳天线是目前对潜通信最为重要和有效的方式。一般情况下，拖曳体系统的构型与内部应力分布对其工作性能影响较大，例如对潜天线的稳态构型垂直距离影响了其信号发射能力，天线的内部应力分布，对其安全性有着重要影响，因此需要对拖曳体的构型、应力等要素进行合理的预测、分析，以确保拖曳系统功能性与安全性。

国外对拖曳体的动力学特性做了较多的研究 ，20 世 纪 60 年代末 ，S. L. Huang、R. A. Skop等提出了针对“塔康木”对潜通信天线稳态构型的数值分析方法，在良好的初值条件下，该方法能够较好地收敛；20 世纪 90 年代，J.M.Clifton基于离散微元的思想，针对微元受力平衡建立了拖曳天线的稳态模型，结果与实测值一致性较好；R.G. Borst 等、F. Zhu 等对风导致的拖曳天线振动等稳定性问题进行了研究；M.I.Friswell基于绳索动力学理论，对水下拖曳绳索稳态构型进行了研究；20 世纪 90 年代以后，P.Williams 等介绍了基于多体动力学理论的拖曳天线建模与仿真研究，对周期性运动的载机—拖曳体模型进行了分析，得到了载机进行圆周、椭圆运动时，拖曳天线的动态响应情况，在此基础上开展了载机非周期运动时，拖曳天线的响应问题研究。

国内对拖曳绳索类问题也开展了较多的研究，贾忠湖和郑小洪等在拖曳天线稳态构型以及稳定性等方面取得了较好的成果。柔性绳索动力学理论及建模方法，作为机载拖曳问题的理论基础，在近些年得到了较为深入的发展，并在船舶、航天等领域开展了大量的工程应用研究。

在上述研究中，对天线的建模研究一般仅考虑拉力，忽略弯曲内力及剪切内力的影响。本文基于一阶梁理论，建立考虑弯曲内力矩、剪切内力以及扭转内力矩的天线结构模型。首先对拖曳天线的稳态构型进行分析，并与文献［5］中的实测结果进行对比；其次基于天线动力学模型，开展载机阶跃、简谐运动时的天线动力学响应问题研究；再次对突风作用下的天线动态响应及稳定性进行评估；最后对天线发生断裂的复杂响应问题进行初步探索。

1 建模方法

1.1 结构模型

取任意一段天线，如图1 所示，基于Timoshenko 一阶梁理论，天线截面位移式矢量为

图1 天线段及其坐标系、截面内力示意图Fig.1 Local coordinate and internal forces of segment of antenna

式中：

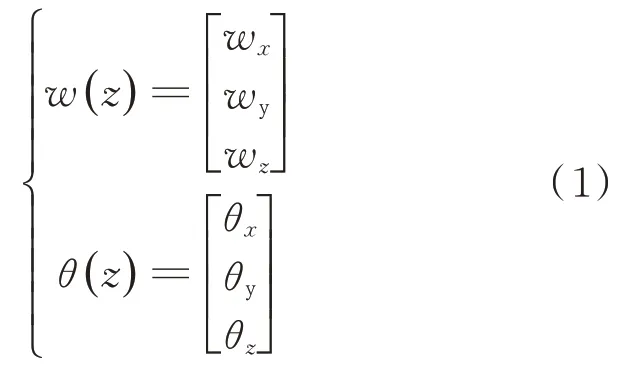
w

、

w

、

w

为天线截面各个方向的线位移；

θ

、

θ

、

θ

为天线截面各个方向的角位移。

取图1 天线段的右侧截面，如图2 所示。

图2 截面应力示意图Fig.2 Stress in the section

由截面变形关系、内力—应力关系以及应力应变关系，可以得到天线截面内力与位移的关系为

式中：

σ

、

σ

、

σ

分别为截面上一点各个方向的应力；

A

为截面积；

A

、

A

为截面剪切面积；

S

、

S

为截面静矩；

I

、

I

、

I

、

I

为截面二次距；

E

、

G

分别为弯曲、剪切模量。

假设天线截面为圆形，天线弯曲与扭转中心均过截面形心，忽略剪切折减系数影响，忽略角度位移诱导的切向力，对式（2）沿天线长度方向积分，则可以得到：

式中：

Q

、

Q

、

N

分别为各个方向的内力；

M

、

M

、

M

分别为各个方向的内力矩；

L

为天线段长度。基于上述推导，可以建立天线结构模型，如图3 所示。将天线离散为若干个长度为

L

的刚性段，其外力、力矩集中作用于其几何中心，刚性段之间由6 元线弹性内力约束，内力—位移表达式如（3）所示。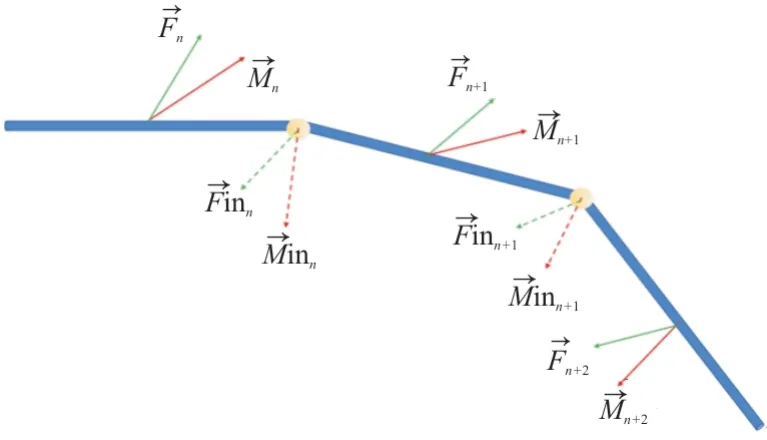

图3 天线刚性分段模型及其受力示意图Fig.3 Rigid segments of antenna and force diagram

1.2 气动力模型

天线的气动力在每个离散刚性段上分别计算，天线的气动力可以分解为径向的气动力分量和轴向气动力分量，其中轴向的气动力对天线系统的动力学影响作用较小，在本文中忽略其影响。对天线径向气动力进行准定常假设，其值由式（4）给出。

式中：

C

为天线径向气动力系数；

d

为天线直径；

l

为天线刚性段长度；

ρ

为当地密度，如式（5）所示；

V

为当地真空速在天线段径向的分量。

式中：

ρ

为海平面空气密度。

为了保证拖曳体在空中的稳定性，一般在末端均有风标，本文仅考虑风标的阻力，如式（6）所示。

式中：

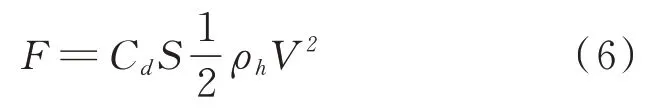
C

为风标的阻力系数；

S

为风标参考面积；

V

为风标的当地真空速；

F

为风轴系的量。由于

F

无法在式（1）中直接使用，因此需要投影至体轴系，如图4 所示，可以看出：在图中所示的坐标轴定义中，转换关系为绕风轴系z 轴转

β

度后至稳定系，再绕稳定系

y

轴转

α

度至体轴系。转换矩阵

L

如式（7）所示，迎角

α

及侧滑角

β

依据刚性段的真空速在体轴系的投影关系计算，如式（8）所示。

图4 气流系到体轴系的转换关系Fig.4 Transformation from wind coordinate frame to body coordinate frame

式中：

u

、

v

、

w

分别为天线刚性段在其自身体轴系

x

、

y

、

z

方向的速度分量；‖

U

‖为速度的模，当迎角与侧滑角超过反正切与反正弦定义域时，依据其定义进行周期性拓展。

1.3 动力学方程与求解

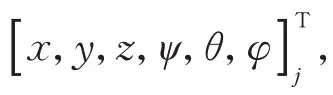
天线系统的约束方程为

式中：

Φ

(

q

，

t

)为运动学约束方程；

Φ

(

q

，

t

)为驱动约束方程。

考虑约束方程，基于拉格朗日乘子法，建立天线多刚体系统的拉格朗日运动微分方程：

式中：

T

为系统的动能；

F

为

q

方向上的广义力；

λ

为拉格朗日乘子。

采用GSTIFF 积分器，通过预测、迭代校正、积分误差分析以及步长优化等步骤，对运动微分方程进行数值求解。

2 稳态构型分析及验证

以“塔康木”天线为计算模型，选取与文献［5］中相同的计算参数：载机稳定盘旋真空速108.083 m/s，载机巡航高度为巡航高度5 585.46 m，载机倾 斜 角 34°，天 线 长 度 6 184 m，天 线 线 密 度0.092 54 kg/m，天线直径0.006 m，天线气动力系数1.03，风标参考质量37.2 kg，参考面积0.29 m，风标阻力系数0.5，质心与压心距离0.25 m。

天线离散为200 个刚性段，计算在时域中进行，以无载机运动时的平衡状态作为初始值，为了使天线容易收敛至稳态构型，缓慢加速载机运动速度至稳定盘旋状态，天线系统不同位置的竖直方向坐标收敛曲线如图5 所示，可以看出：本文所建立的模型收敛性较好。

图5 天线不同位置垂竖直方向坐标收敛过程Fig.5 Convergence process of vertical coordinates in different positions of antenna

天线稳态构型仿真结果如图6 所示，可以看出：天线稳态构型与“塔康木”等典型对潜通信天线的稳定构型形态基本一致，证明本文所研究的动力学模型对拖曳天线的稳态构型形状计算结果较为准确。

图6 稳定构型仿真结果Fig.6 Simulation results of steady state configuration

风标的轨迹在水平面的投影是拖曳天线稳定性的指标之一，风标的水平方向的坐标随时间变化规律如图7 所示。

图7 风标质心水平面的收敛过程Fig.7 Convergence process of the center of mass of the drogue in the horizontal plane

从图7 可以看出：在载机的牵引下，风标开始运动，其水平方向坐标在初始扰动后很快收敛于形状固定的环形区域（如图8 所示），不随时间推进而改变，此项计算结果与该天线的在实际应用中的稳态构型在形态上较为一致，表明了本文建模方法的有效性。

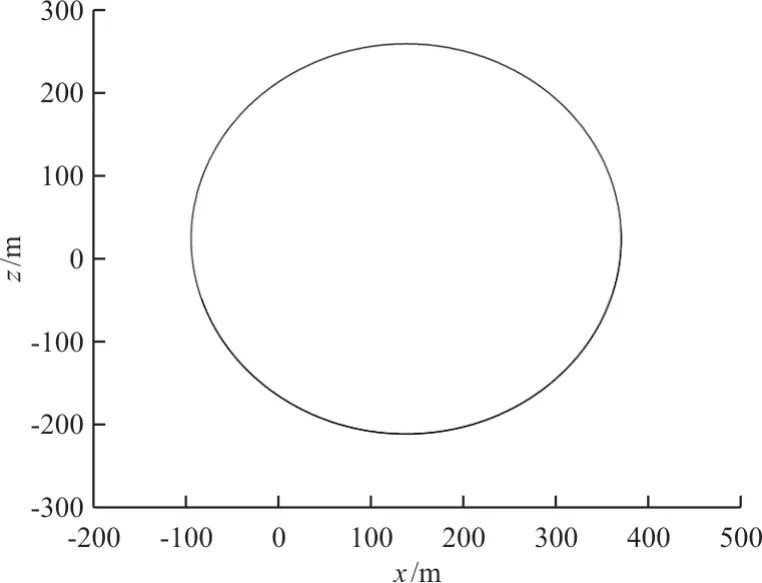
图8 稳定状态下风标质心水在平面的轨迹Fig.8 The trajectory of the center of mass of drogue in the horizontal plane

拖曳天线一般工作在甚低频波段，为了实现良好的信号发射，天线长度一般应不低于信号波长的一半，因此天线稳态构型的竖直方向长度（垂直度）以及坐标分布是此类问题研究的重点。本文方法所计算的竖直方向坐标相对弧长分布与文献［4-5］的结果对比如图9 所示，可以看出：两种计算方法所得的天线末端高度几乎一致，天线各个弧长位置下的竖直方向坐标分布一致性较好，证明了本文建模方法在天线垂直度计算方面的准确性。

图9 天线稳态构型垂直坐标Fig.9 Vertical coordinate distribution of the antenna in the steady state

拖曳天线的另一个研究重点为拉力分布问题，沿天线长度任何位置的拉力，不应大于天线的强度极限，否则将导致结构失效，因此需要对拉力进行准确预测。本文建模方法所计算的拉力相对弧长分布与文献［4-5］的结果对比如图10 所示，可以看出：两种计算方法所得的拉力在天线末端一致性较好，总体趋势上较为吻合，但在靠近载机的区域，本文建模方法计算的拉力值要小于文献中的结果。

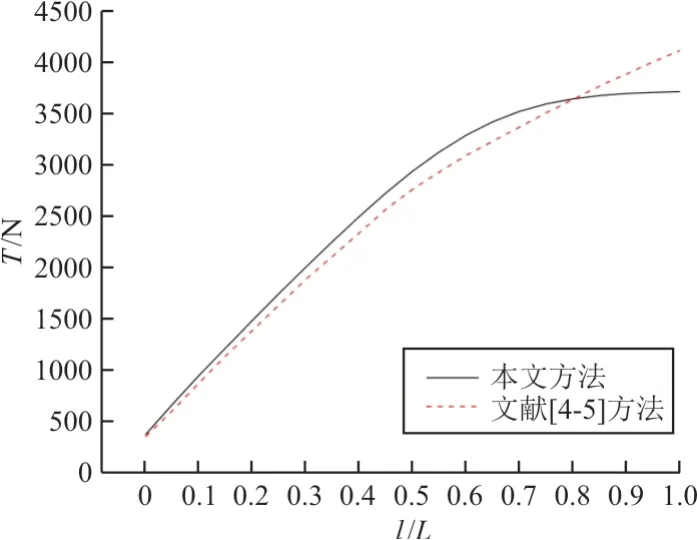
图10 天线稳态构型拉力的分布Fig.10 Tension distribution of the antenna in the steady state

基于Timoshenko 一阶梁理论天线建模方法，不仅考虑了天线轴向的刚度，还包含了剪切效应、弯曲效应以及扭转效应，因此与文献［4-5］中仅考虑拉伸的建模方法相比，天线稳态构型拉力值有所差异，本文的建模方法更为合理。

3 瞬态响应研究

3.1 载机垂直机动分析

飞机在飞行中，受突风或者大气湍流影响，可能会出现纵向位移扰动，因此在稳态分析结果的基础上，引入纵向位移扰动，分别为阶跃以及简谐形。

载机阶跃运动规律由式（11）、式（12）给出。

式中：

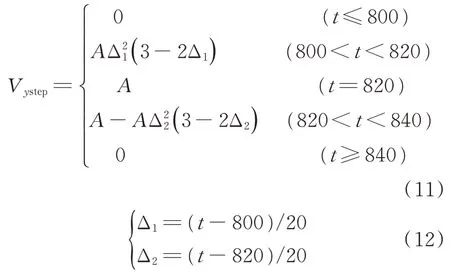
V

为载机纵向速度；

A

为幅值，取值25 m/s。

在该运动规律的作用下，载机的纵向位移曲线如图11 所示。天线的构型受载机运动扰动后，偏离稳态位置，并重新收敛，风标的纵向位移曲线如图12 所示，载机和天线的连接点拉力曲线如图13 所示，可以看出：在载机阶跃位移扰动的作用下，天线系统的构型和内力等方面的稳定性较好。

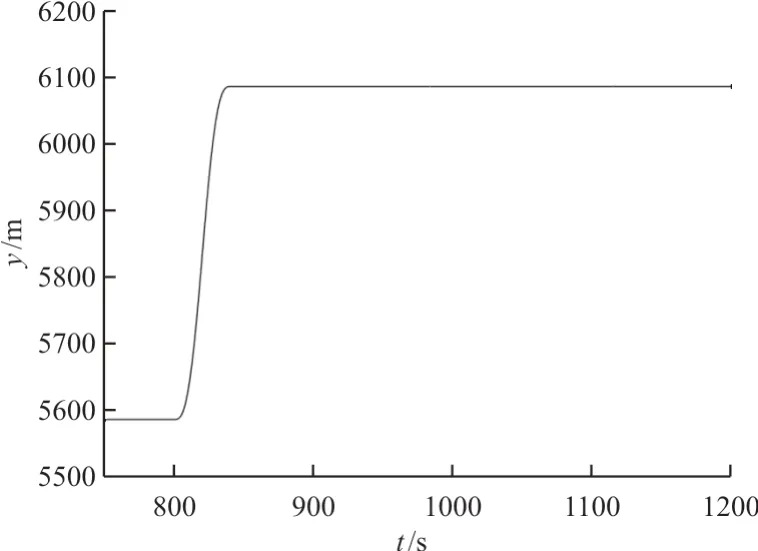
图11 载机竖直方向阶跃形位移曲线Fig.11 Step displacement of the aircraft in vertical direction

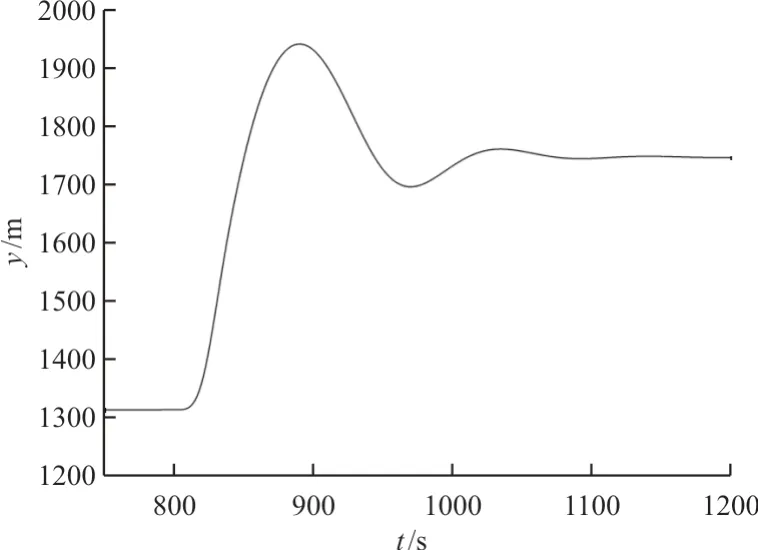
图12 风标竖直方向位移受载机阶跃运动影响变化曲线Fig.12 Vertical displacement of the drogue due to the step movement of the aircraft

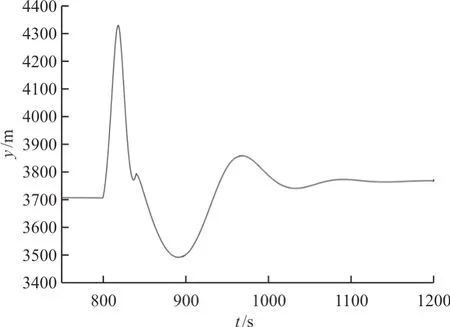
图13 载机受天线拉力随载机垂直运动影响变化曲线Fig.13 The change of tension between aircraft and antenna due to the step movement of the aircraft

载机简谐运动规律由式（13）给出。

式 中 ：

f

为 频 率 ，取 值 0.1 Hz；

A

为 幅 值 ，取 值25 m/s。

在该运动规律的作用下，载机的纵向位移曲线如图14 所示。天线风标的纵向坐标（如图15 所示）、载机和天线的连接点拉力（如图16 所示）也呈现同频简谐振动，天线拉力变化值与阶跃位移扰动相比，较为显著。

图14 载机竖直方向简谐形位移曲线Fig.14 Harmonic displacement of the aircraft in vertical direction

图15 风标竖直方向位移受载机简谐运动影响变化曲线Fig.15 Vertical displacement of the drogue due to the harmonic movement of the aircraft

图16 载机受天线拉力随载机简谐运动影响变化曲线Fig.16 The change of tension between aircraft and antenna due to the harmonic movement of the aircraft

风标水平方向的坐标规律如图17 所示，可以看出：扰动前及扰动后的轨迹均为环形，且坐标绝对值差量较小。上述计算结果表明，载机纵向简谐运动对天线的形态影响较小，但对天线拉力的变化存在一定的影响，应该在应用中加以关注。

图17 风标水平方向位移受载机简谐运动影响变化曲线Fig.17 Horizontal displacement of the drogue due to the harmonic movement of the aircraft

3.2 水平突风扰动

突风除了能够影响载机的位移，同时也能够以气动力的方式直接作用在天线上，对天线产生影响，因此需要考虑天线模型在大气扰动（水平突风）情况下的动态响应。

将突风速度投影至天线当地坐标系，以速度增量的形式影响天线当地径向速度

V

，进而实现对气动力

F

的影响。所采用的突风作用方式为：在沿天线方向上，仅最靠近中心的三个刚性段处，受到速度为51.44 m/s（100 节/小时）的持续水平突风扰动。

突风作用下的风标竖直方向位移曲线如图18所示，可以看出：持续的水平突风，使风标纵向位移出现周期性等幅振荡，且振幅较大。

y′z′=S31x2+S32xy+S33y2+(1+S34)yz+S35z2+S36zx+S37x+S38y+S39z+S40+o(h2)

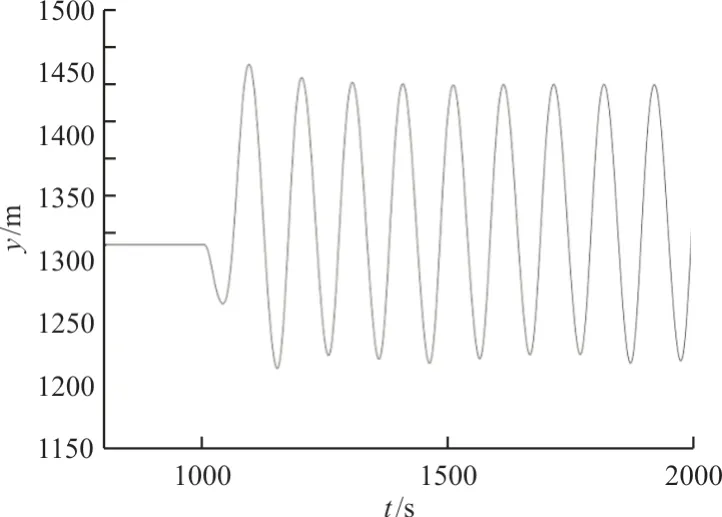
图18 突风作用下的风标竖直方向位移曲线Fig.18 Vertical displacement of the drogue due to the gust

水平方向的位移坐标轨迹（如图19 所示），在突风扰动后，也出现较大的位置偏移，但在几个周期后能够重新趋于稳定，且前后形状差异不大。

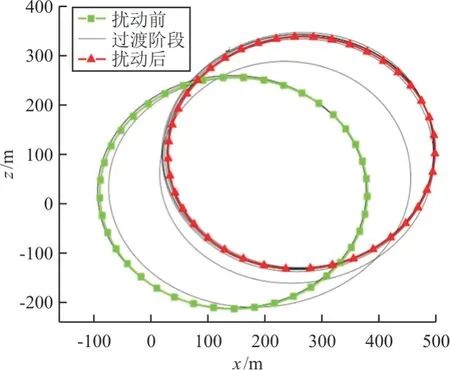
图19 突风作用下的风标水平方向位移曲线Fig.19 Horizontal displacement of the drogue due to the gust

突风作用下的载机与天线连接点拉力曲线如图20 所示，可以看出：天线与载机连接点的拉力受突风影响，也出现周期性等幅振荡。

图20 突风作用下的载机与天线连接点拉力曲线Fig.20 The change of tension between aircraft and antenna due to the gust

持续水平突风，使天线的稳态构型发生了改变，且带来了天线形状以及拉力的周期性振荡，与载机纵向位移带来的扰动相比，对天线的影响更大。

3.3 天线断裂分析

拖曳天线使用中需要经常收放，进而出现磨损，同时使用过程中的外部扰动带来的周期性振荡会加速结构的疲劳，在极端情况下，天线会出现断裂情况。

天线断裂，不仅会导致功能失效，断裂的天线也会极大地威胁载机的飞行安全，因此需要对此进行研究。文献［11-13］基于微元受力平衡所建立的天线动力学模型，一般为非线性、强耦合的偏微分方程组，采用Galerkin 等数值方法进行求解时，需要引入满足天线边界条件的（连续）形状函数，无法处理天线的瞬态断裂问题。

本文通过使控制方程中的指定约束失效（约束内力置零），实现对天线断裂效果的模拟，断裂点选取为天线几何中点。天线中点位置断裂后的天线空间分布规律如图21 所示。以稳态构型为初始状态，断裂后，下半段天线因失去拉力而下坠，未出现上扬等危险状态，而上半段天线迅速趋于水平，存在与载机碰撞的潜在危险。

图21 天线断裂后的空间分布变化规律Fig.21 The change of spatial distribution of antenna segments after structural failure

上半段天线末端的纵向位移曲线如图22 所示，可以看出：在天线断裂后，其纵向坐标迅速增大，与载机纵向坐标差距不足1 000 m，且呈现高度随机摆动特征。

图22 上半段天线末端的纵向位移曲线Fig.22 Vertical displacement of the end of the remaining part of the antenna

载机受残余天线的拉力情况如图23 所示，可以看出：虽然由于天线质量减少、气动力减少而导致拉力的均值低于断裂前，但天线末端的随机运动导致拉力方差较大，较大的峰值对载机的姿态影响也较大。

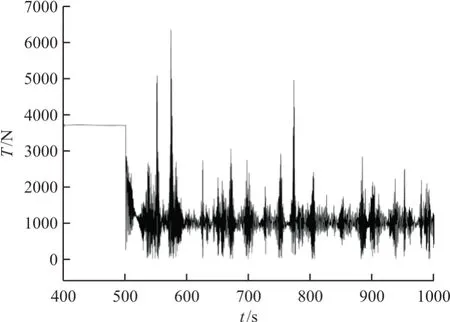
图23 断裂后载机与天线连接点的拉力曲线Fig.23 The change of tension between aircraft and antenna due to the structural failure

4 结 论

（1）本文所建立的模型得到的稳态结果与文献［5］中的结果规律与绝对值均一致性较好，因此本文所建立的方法有效、准确。

（2）本文所建立的模型能够用于拖曳天线系统的复杂瞬态分析，如阶跃、简谐形的载机纵向机动对天线的影响进行分析，突风对载机—天线动态特性影响分析，所得到的天线位置、内力瞬态变化规律等可以用于天线性能与强度设计等工程问题。

（3）与基于Galerkin 等方法相比，本文所建立的模型与方法能够处理天线断裂等非线性问题，分析天线断裂后的拉力与空间位置分布，对恶劣工况下的天线系统设计与安全评估有一定的工程参考价值。