RF 航段衔接ILS 进近程序的最大下降角设计方法

赖欣，赵得存

（中国民用航空飞行学院空中交通管理学院，广汉618307）

0 引 言

飞行程序设计的质量对航空运行安全起着重要作用，规范的设计流程与设计方法对设计质量的提升有较大促进作用，设计过程中的关键参数选择影响飞行安全。基于性能导航程序（PBN）的所需导航性能（RNP）通过星基导航定位点规划航迹，具有航迹规划灵活且能有效减少飞行路径、降低燃油排放的优势。同时RNP 航段在设计过程中须考虑的保护区范围相比其他程序设计方式也更窄，尤其适合在净空及空域受限的机场实施进场、起始进近阶段程序设计。仪器着陆系统（ILS）引导的精密进近方式是目前全球使用最为广泛的最后进近着陆方式。各大中型机场都以仪表进近程序作为机场的首选进近方式。将RNP 航段和ILS 进近程序结合能在飞行安全、节能减排与环境保护等方面发挥两者优势。但实现这种程序的衔接需要在两种程序设计方法之间进行转换，RNP程序属于星基程序设计规范，ILS 程序属于传统陆基程序设计规范。同时还需考虑从基于卫星导航的RNP 航段实施完成后，转为陆基无线电信号程序所需解决的无线电信号稳定截获问题。

目前国际上主流的飞行程序设计标准为国际民航组织（ICAO）的 8168 标准与美国美国联邦航空局（FAA）的 TERPS 标准，两类程序设计标准在设计思路上一致，但在设计的技术细节上存在差异。FAA TERPS 标准总结了在 RNP 程序与ILS 程序结合的设计要点，并通过分析多种航空器模型提出了该类程序设计指南，但未就如何设计两种程序过渡的下降剖面给出方法。D.Smedt 等根据 ICAO 8168 标准通过飞行模拟方法对两种程序的过渡阶段进行了研究，但并未针对两种程序过渡阶段的最大下降角度提出设计方法。因此目前在实际工程设计中，都是通过设计人员根据经验进行预估，再通过反复试算的过程来进行设计。

人工试算准确度低，设计效率不高，针对这一问题，本文对衔接两种程序阶段的过渡进近航段的设计方法进行研究。首先分析两种程序的结构特点，总结过渡航段设计过程中下降剖面几何关系形成的设计参数限制，给出过渡程序运行阶段无线电信号稳定截获的运行限制；在同时满足参数几何关系与信号稳定截获的限制下，提出一种计算过渡航段最大下降角度的方法，并进行仿真验证。

1 ILS 精密进近与RF 航段结构分析

ILS 进近程序是目前国际上主要采用的最后进近方式，该程序方式采用进近跑道末端安装的航向台LOC 与进近跑道侧方安装的下滑台GS，形成两组空中无线电信号，航向台信号引导航空器对准着陆跑道，下滑台信号引导航空器建立正确的下滑剖面。ILS 程序分为起始进近段、中间进近段与精密进近段，其中起始进近段可采用不同程序模式，但要求该段结束的中间进近定位点IF 必须位于ILS 航向信标的作用范围内，以保证在完成起始进近航段后能结合航向信号，即IF 通常是航空器截获航向台的最晚位置点，即FACF。程序至最后进近点FAP 后进入精密航段，该航段要求航空器能在保持航向引导的同时结合下滑台信号，从而保证在最后进近阶段能同时获得航向台与下滑台信号引导，直至完成着陆。IF 到FAP 的中间进近航段是将起始进近航段与精密航段平滑安全连接的关键航段。

RNP 程序航路点由导航数据库提供，以卫星定位的形式实施导航。航迹布局灵活，比如其中的固定半径转弯航段即RF 航段，可以设计转弯在2°～300°之间的弧线。RF 航段平面图与剖面图如图1 所示。

图1 RF 航段平面结构与剖面结构图［4］Fig.1 Plan and profile structure of RF segment［4］

从图1 可以看出：将RF 航段作为ILS 程序的起始航段，则是利用RF 航段的

P

至

P

航段的固定点半径转弯部分，

P

应为截获航向最晚位置即ILS精密进近的中间进近定位点，RF 航段的

P

至

P

即为ILS 程序的中间进近航段，

P

应为截获下滑最晚位置点即ILS 精密进近的FAP，在进近至

P

点之前应完成航向信号截获，从

P

至

P

中间进行阶段应保持航向信号，并完成下滑台信号截获，而两点中间进近实施完成后的位置高度，决定了ILS 精密进近下滑过程的稳定性。

2 过渡航段分析

由上节分析可得RNP 航段与ILS 精密进近航段的衔接关键是过渡，即中间进近航段，RF 航段衔接ILS 精密进近的过渡航段平面与剖面图如图2所示。

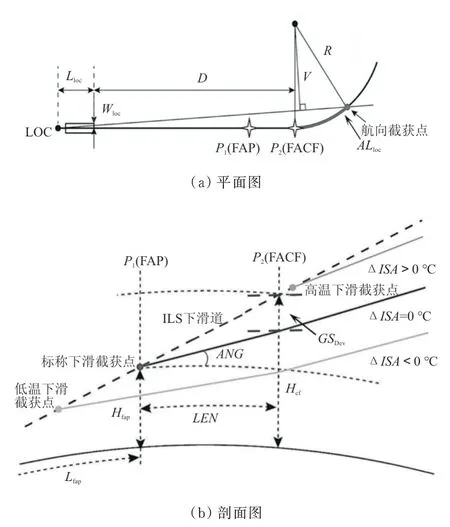
图2 过渡航段平面与剖面结构［9-10］Fig.2 Plan and profile structure of transition phase［9-10］

在起始进近阶段即RF 航段阶段，航空器将开始建立航向，实际截获航向位置点将在RF 航段实施过程中某一点，最晚不应晚于FACF，该点至FACF 的弧长为

AL

，

航空器截获航向后将有一个稳定保持距离，如图2（a）所示。实际截获下滑台的位置点也将在RF 航段实施过程中某一点，最晚不应晚于FAP。在RF 航段设计规范中要求，标称航迹应在△

ISA

＝0 ℃假设温度下设计。而实际RF 航段下滑剖面与实际运行温度有关，当温度高于或低于△

ISA

＝0 ℃时（如图2（b）所示），实际下滑截获点的位置会有变化。为保持过渡航段稳定截获下滑信号，需要考虑在可能的最高温下该航段应具有的最大下降角度即

ANG

的最大值，该值须能保证在起始进近的下降执行效率，也须避免因

ANG

值过高而导致后续精密进近无法稳定建立。为讨论

ANG

最大取值建立方法，结合图2 的平面与剖面几何关系，可以得到设计所需的参数。

L

是从跑道入口（THD）到最后进近点（FAP）的水平距离，考虑地表曲率，可以根据几何关系计算得到。

式中：

r

为地球半径；

H

为基准交叉点高度；

θ

为滑坡角（标准为 3°）；

H

为标称 FAP 高度。

标称最后截获航向定位点高度，可计算如下：

式中：

LEN

为从 FAP 到 FACF 的距离；

ANG

为下降角。航向截获点到FACF 的弧距

AL

计算如下：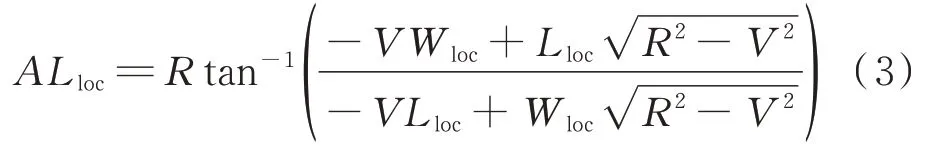

式中：

W

为航向台波束在跑道入口THD 处的宽度；

R

为 RF 段的固定半径；

V

为从 RF 航段转弯中心到航向捕获点与航向台之间连线的垂直线的距离。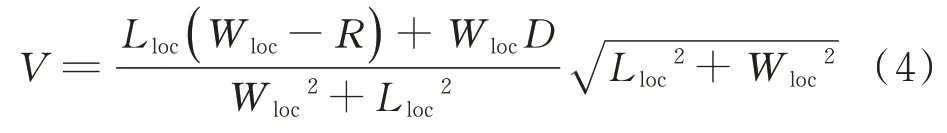

设计过程中非标准温度需与标准设计温度

ISA

＋15 ℃进行校正，校正值为

式中：Δ

T

为与标准温度（

ISA

＋15 ℃的平均海平面）的温度差；

L

为

ISA

的第一层（海平面至对流层顶）的压力高度；

T

为海平面的标准温度；

h

为THD 在平均海平面以上的高度。

3 过渡航段最大下降角计算方法

过渡航段设计过程中须预设最高温度，温度差在所有海拔高度上都是恒定的。由运行过程分析可知，在RF 航段实施过程中温度不会影响航向截获点位置，而下滑截获点位置会因为温度影响导致ILS 下滑道与RF 航段VNAV 垂直剖面上存在高度上的偏差

GS

，如图2（b）所示。过渡航段（中间航段）的下降角将取决于

GS

，在温度逐步抬升的设计条件下，当

GS

最大时将对应满足几何条件的最大航段下降角

ANG

。但如果

GS

值过大，将导致在FAP 点后航空器无法截获下滑台，从而无法在精密进近航段同时活动航向与下滑信号引导，只能转为非精密进近模式。由于从不同FAP 高度可计算下滑道的偏离量，因此条件可以从下滑信号捕获点到最后航向截获点FACF 的弧距离关系进行判断，即

AL

＜

AL

，

AL

为下滑信号捕获点到 FACF 的距离。由上述参数几何关系与实际运行要求，本文提出过渡航段最大下降角度（

ANG

）计算方法，计算流程如图3 所示。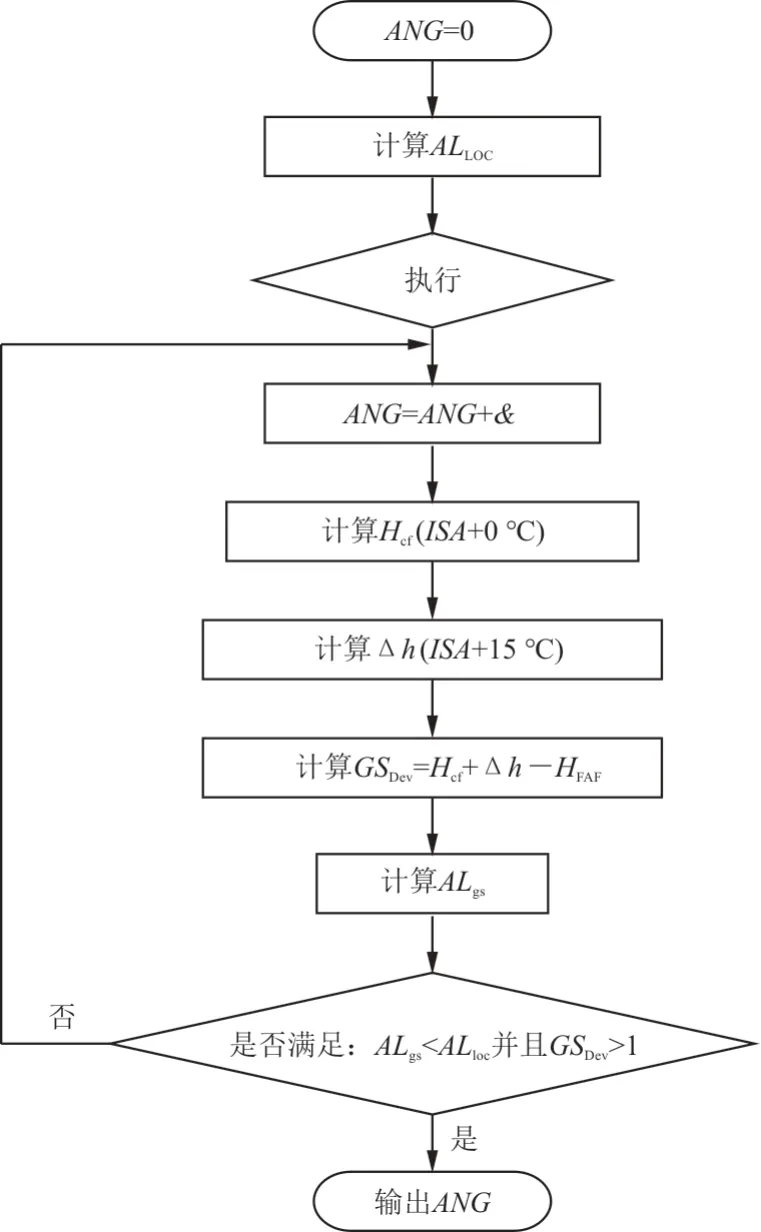

图3 过渡航段最大下降角计算流程图Fig.3 Maximum descent angle calculation flow diagram for transition phase

计算过程需首先设定

ANG

初始值为0°，并使用公式（3）计算

AL

。&为

ANG

角度增量，利用公式（2）在

ISA

温度下计算

H

。随后在

ISA

+15 ℃下，使用公式（5）对最高温度高度进行校正；计算不同高度下的下滑道偏离

GS

；由精密进近航段设计评估计算可获得最后进近定位点高度

H

。利用公式（3）计算从滑坡截获点到FACF 的弧长，如果

AL

＜

AL

且最大下滑坡度偏差大于1，则算法输出的

ANG

为最大下降角。

4 仿真计算与结果分析

根据提出的最大下降角设计方法，本文利用Matlab 进行仿真计算。计算过程设定程序设计参数 为 ：最 高 温 度

ISA

+30 ℃，RF 固 定 半 径2.5 n mile（1 n mile=1.852 km），入口跑道标高500 f（t1 ft=0.304 8 m），

L

=4 300 m，

W

为标准参数 210 m。为考虑各类精密进近超障的可能性，最后进近定位点高分别假定为1 000～4 000 ft，以500 ft 为计算增量。根据设计规范要求，中间进近航段

LEN

需等于或大于 1 n mile，因此假设

LEN

从1 n mile 输入计算流程，并以0.1 n mile 为增量至2 n mile；

ANG

初始值为 0°，并以 0.01°为增量。通过仿真计算得到不同最后进近定位点高度与过渡航段长度组合下的最大下降角如表1 所示。

表1 不同组合参数条件下最大下降角Table 1 Maximum descent angle under different parameters

根据表1 数据得到的曲线图如图4 所示，可以看出：根据本文提出的方法在最高假设温度基础上，可以在不同过渡航段长度与最后进近定位点高度上计算得到一个最大中间航段下降角度

ANG

，且最大

ANG

值均小于 2°，与 FAA 提出的设计指南保持一致，即在RF 航段和FAP 之间设计的过渡段具有角度不超过 2°的“浅下降角”；最大

ANG

输出与现实飞行过程一致，当FAP 点的高度较低时，为衔接起始进近阶段并保证有效截获航向信号与下滑信号，下降角度将较大，即相同过渡航段长度，过渡航段需要消失的高差越大下降角度也将越大。需要说明的是

ISA

+15 ℃为程序设计中常用理论温度基准，若程序设计环境的标准温度不是

ISA

+15 ℃，那么

ISA

取值会直接影响

GS

，进而影响

ANG

。

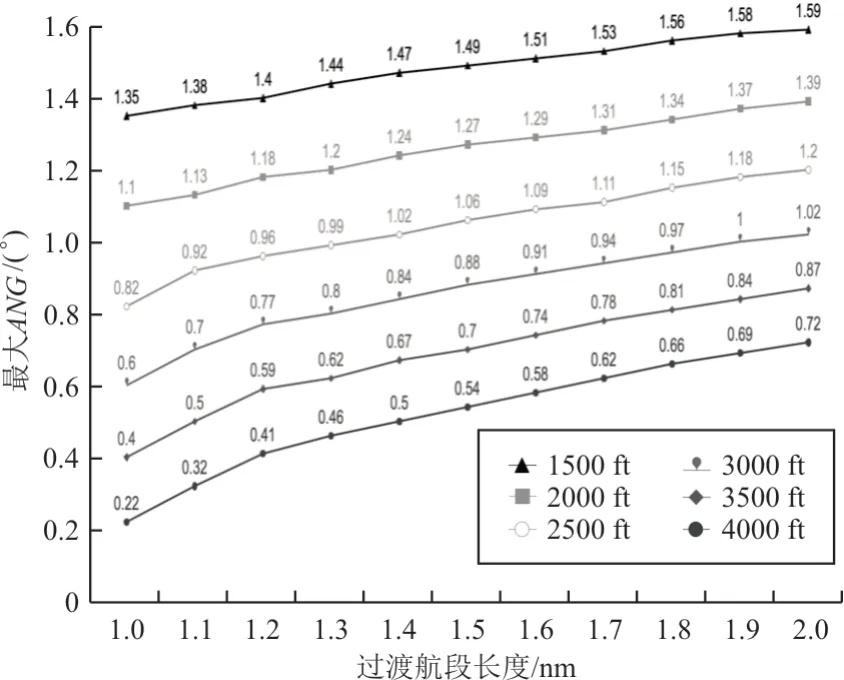
图4 不同组合参数条件下最大下降角Fig.4 Maximum descent angle under different parameters

5 结 论

（1）本文提出一种RNP 程序RF 航段过渡至ILS 精密进近程序的最大下降角度设计方法，并构建了过渡阶段最大下降角度的计算流程，采用不同参数组合条件下的模拟验证，证实了该方法的可行性。提出的设计方法相较与目前的人工试算方法具有更高效率。

（2）为满足两类程序设计规范在几何空间中的衔接要求，过渡航段的下降角取决于ILS 下滑道与RF 航段VNAV 垂直剖面上存在的高度偏差

GS

，在温度逐步增加的设计条件下，当

GS

最大时将对应满足几何条件的最大航段下降角

ANG

。（3）在从RF 航段的星基导航转为ILS 进近的陆基导航，需要航空器在FAP 截获下滑台信号，若

GS

值过大，将导致在FAP 后航空器无法截获下滑台，从而无法在精密进近航段同时活动航向与下滑信号引导，只能转为非精密进近模式。因此可以从下滑信号捕获点到最后航向截获点FACF 的弧距离关系进行运行限制条件的判断。

（4）以逐步增量逼近的方式，采用空间几何参数限制与运行限制条件作为增量循环的判断条件，能够快速计算过渡航段的最大下降角度取值。