飞行器栖落机动轨迹可达域分析

杜昕，黄江涛，章胜

（中国空气动力研究与发展中心空天技术研究所，绵阳621000）

0 引 言

超短距起降固定翼飞机具有飞行速度快、运载能力强、环境适应性好等优点，这些特点是普通直升机所不具备的。因此，超短距起降固定翼飞机适用于驱护舰，可以取代并拓展大多数的直升机任务与使用模式，同时具有更低的使用成本和高可靠性。固定翼飞机的舰上起飞尚可以通过弹射实现，但是如何在驱护舰上狭小的空间内实现安全降落，是一个亟待解决的关键技术问题。

栖落机动是解决该问题的有效途径之一。栖落机动是指飞机利用大迎角产生高阻力从而实现超短距离减速和着舰，是一种超机动飞行方式，其灵感来源于鸟类的定点着陆方式。

关于栖落机动的相关研究，国外起步较早，约2000 年左右就开展了一系列较为充分的研究，主要集中于需求与概念论证、栖落过程的大迎角非定常气动力建模、栖落轨迹优化、栖落机动标称轨迹跟踪控制等方面。由于小型滑翔机只有一个控制变量，且重量轻，容易实现大迎角机动，早期被广泛用来开展相关研究。但是小型滑翔机装载容量与重量十分有限，无法安装惯导系统，为了解决这个问题，麻省理工大学的研究人员采用光学定位手段来确定飞行器的位置、速度与姿态信息，并在室内开展了小型滑翔机的定点栖落试验。为了解决大迎角栖落末端机身的固定问题，斯坦福大学的研究人员设计了一种带有钩爪的小型固定翼飞机，当机载超声波装置探测到离墙面的距离足够近时，钩爪伸出钉入墙面将飞机固定，钩爪松开后飞机可由墙面实现起飞。栖落轨迹优化研究主要关注优化轨迹的分段、优化指标的选择以及优化策略的对比分析。在栖落轨迹跟踪控制方面，现有的轨迹跟踪控制算法经过适应性改进都可以应用到栖落问题中来。由于栖落过程的大迎角非线性特性，许多线性控制方法不能直接使用，因此出现了分段线性控制、线性二次型调节树等方法，而非线性方法则有动态逆解耦、非线性最优控制等。

国内关于飞行器栖落机动的研究起步较晚，研究较少，南京航空航天大学的何真团队近年来开展了一些研究，主要集中在气动参数辨识、轨迹优化以及轨迹跟踪控制等方面。总的说来，现有的研究缺少对栖落任务总体方案的研究与分析。

本文在前人有关栖落轨迹优化的相关研究的基础上，从总体设计的角度出发，研究飞行器栖落轨迹的可达域（Reachable Set，简称RS）。首先对栖落轨迹可达域进行定义并给出数学描述，然后建立可达域计算的轨迹优化模型，最后采用高斯伪谱法求解可达域的边界轨迹。

1 飞行器栖落机动建模

飞行器栖落机动的纵向动力学模型如式（1）～式（6）所示。

式中：

V

为飞行器纵向飞行速度；

γ

为飞行航迹角（飞行速度与水平面的夹角，向上为正）；

α

为迎角；

q

为俯仰角速度；

x

为水平飞行距离；

h

为飞行高度；

T

为飞行器推力；

L

为升力；

D

为阻力；

M

为俯仰力矩；

I

为纵向转动惯量；

m

为飞行器质量；

g

为重力加速度（这里可以设为常值

g

=9.8 m/s）。

升力、阻力及俯仰力矩的计算公式如式（7）～式（9）所示。

式中：

C

、

C

和

C

分别为升力系数、阻力系数和俯仰力矩系数；

ρ

为大气密度；

S

为参考面积；

c

为平均气动弦长。本文采用微型无动力滑翔机模型，故

T

=0，飞行器的相关参数如表1 所示。

表1 飞行器参数［19］Table 1 Perching UAV physical constants［19］

栖落机动涉及大迎角气动力建模问题，关于这方面的研究有很多。本文采用的气动模型详见文献［22］，它是以大迎角气动特性的理论模型为基础，通过大迎角飞行实验数据辨识得到气动系数关于迎角的拟合函数。

式中：

δ

为飞行器升降舵偏角，是无动力滑翔机栖落机动的唯一控制量。

2 栖落轨迹可达域求解方法

2.1 栖落轨迹可达域问题数学描述

可达域与可控域是一组数学概念，本文首次将其引入飞行器栖落机动轨迹的研究。如果某一飞行器初始状态确定，那么飞行器能够满足栖落条件的所有终端状态的集合就是该飞行器栖落机动的可达域。反过来，如果飞行器终端条件确定并满足栖落条件，那么飞行器所有能够达到这一终端条件的初始状态集合就是飞行器栖落机动的可控域。分析清楚可达域与可控域，对于栖落机动任务的总体设计、栖落位置的选择、进入状态的约束等等，都有着十分重要的指导作用，为标称轨迹的离线设计和在线轨迹规划提供清晰的理论依据。本文研究针对可达域，对于可控域的研究可在后续开展。

飞行器的状态量定义为

飞行器的初始状态记为

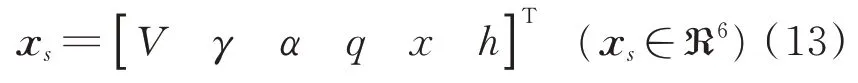
x

(

t

) =

x

(0) =

x

，飞行器在时刻

t

的状态为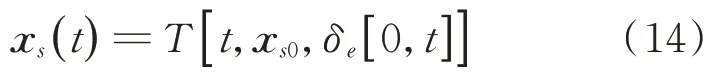

式中 ：

δ

[0，

t

]为从 0 时刻到

t

时刻的 升降舵偏角剖面。

δ

[ 0，

t

]的容许集

U

(

t

)可写成如下形式：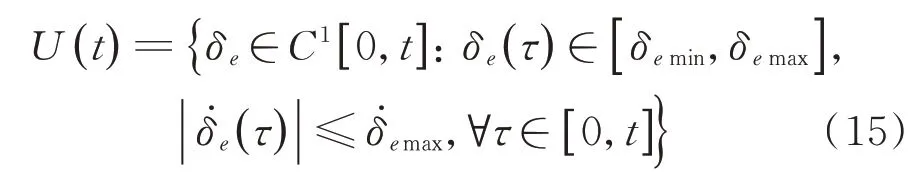

式中：

C

[0，

t

]为在时间区间[0，

t

]上一阶可导的连续函数。若

φ

(

x

) ＜0 为飞行器状态需要满足的不等式约束，定义：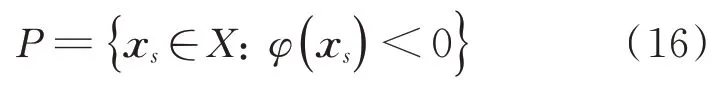

当飞行速度小于给定值

V

，并且迎角大于给定值

α

时，认为飞行器达到栖落终端条件，定义栖落终端状态域

G

⊂

X

为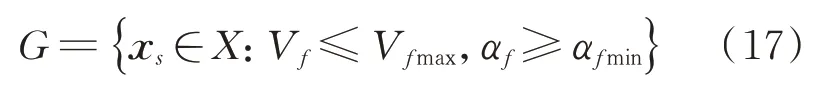

可行的栖落轨迹是指升降舵偏角函数在其容许集

U

(

t

)内，满足飞行器状态约束，且终端状态在

G

内的轨迹。可达域

RS

(

x

) ⊂

G

是指从初始状态

x

出发的可行轨迹所能达到的终端状态的集合，表示为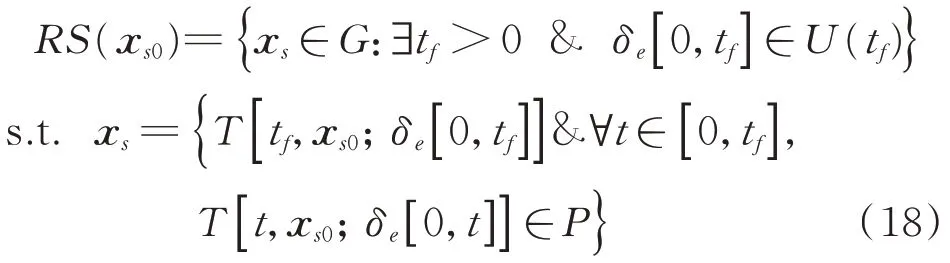

这样得到的可达域是一个包含六个状态量的集合，而实际需要的可达域是指飞行器终端的位置（即水平位置和高度）。因此，本文定义栖落轨迹可达域为

RS

(

x

)在高度

h

和水平位置

x

组成的二维平面上的投影。

2.2 优化模型与求解策略

计算飞行器栖落轨迹可达域实质是计算可达域的边界。对于无动力栖落轨迹来说，轨迹终端状态不存在高度的下边界，因此需要根据任务实际情况，人为规定一个终端高度的下边界

h

。而终端高度的上边界

h

需要优化计算得到。假设初始时刻高度为0，初始状态确定，优化的目标函数为

优化计算得到终端高度上边界之后，再加上人为给定的终端高度下边界，就可以在终端高度的上边界和下边界之间选取一系列离散点，在这些点上优化计算终端水平位置的最大值和最小值，相应的优化模型如下。

假设初始时刻水平位置为0，计算最小终端水平位置时，目标函数为

式中：

x

为给定的终端水平位置最大值，计算时一般给定一个较大的值。

此时，终端高度约束变为等式约束：

式中：

h

为终端高度上下边界之间的某个值。

高度离散点取的越多，计算出的可达域边界就越精确，计算耗时也更长。

因为可达域的求解需要计算很多条边界轨迹，计算量较大，而高斯伪谱法的特点就是计算精度高且速度快，故本文采用高斯伪谱法来求解上述所有优化问题。

3 可达域求解结果与分析

栖落机动初始状态如表2 所示，飞行器状态的路径约束如表3 所示。

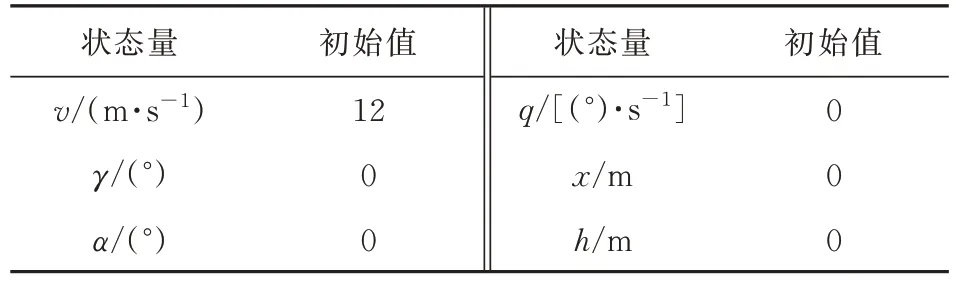
表2 飞行器初始状态Table 2 Initial state of perching UAV

表3 飞行器状态路径约束Table 3 Path constraints of perching UAV state

飞行器初始速度为12 m/s，设定终端速度小于2 m/s 达到栖落终端速度条件，即

V

=2 m/s。升降舵偏角范围设定为-30°≤

δ

≤30°。终端高度下边界设定为

h

=-2 m，终端高度上边界采用高斯伪谱法计算得

h

=1.34 m。在[

h

，

h

]的终端高度范围内选择离散点如下：-2.00，-1.50，-1.00，-0.50，0，0.50，1.00，1.34 m。然后计算每个终端高度处的水平位置最大值和最小值。终端高度约束

h

=

h

时的轨迹优化结果如图1～图2 所示，可以看出：终端水平位置最大和最小时的轨迹几乎重合，由于飞行器控制能力有限，飞行器要在终端以大迎角姿态爬升到

h

的高度，轨迹的可调余量很小。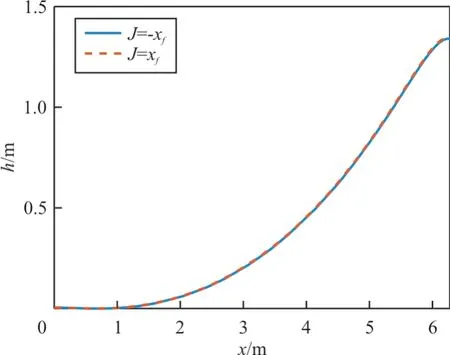

图1 上边界轨迹的空间位置曲线（hf=hup）Fig.1 Position profile of boundary trajectory（hf=hup）

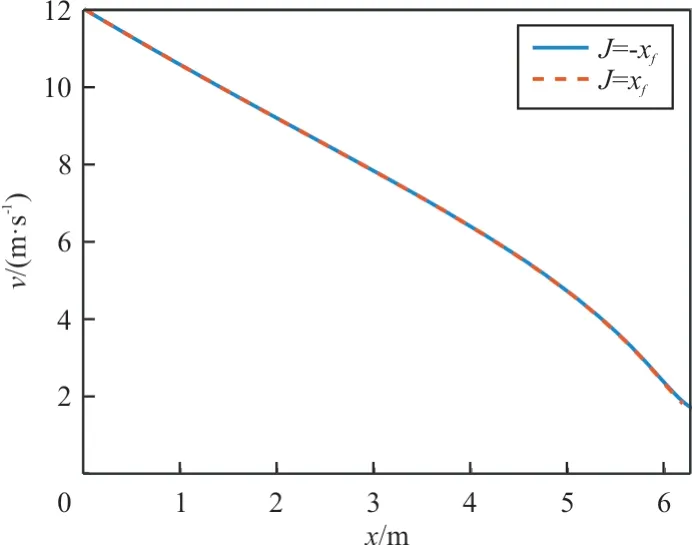
图2 上边界轨迹的速度变化曲线（hf=hup）Fig.2 Velocity profile of boundary trajectory（hf=hup）

终端高度约束

h

=0 时的轨迹优化结果如图3～图4 所示，可以看出：终端水平位置最大的轨迹曲线是先爬升后下滑，速度下降率是先快后慢；而终端水平位置最小的轨迹曲线是先下滑后爬升，速度下降率是先慢后快。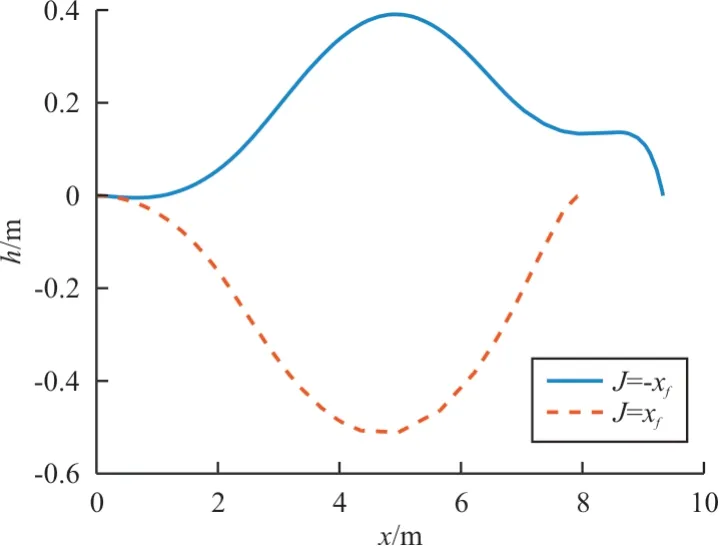

图3 上边界轨迹的空间位置曲线（hf=0）Fig.3 Position profile of boundary trajectory（hf=0）

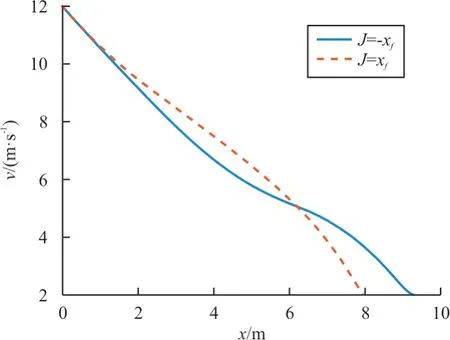
图4 上边界轨迹的速度变化曲线（hf=0）Fig.4 Velocity profile of boundary trajectory（hf=0）

终端高度约束

h

=

h

时的轨迹优化结果如图5～图6 所示，可以看出：终端水平位置最大的轨迹曲线是先爬升后下滑，速度下降率是先快后慢，但速度并不是全程单调递减的，中间有一段速度不变甚至轻微增大的历程；而终端水平位置最小的轨迹曲线同样是先下滑后爬升，下滑段较长而爬升段较短，速度下降率依然是先慢后快。

图5 下边界轨迹的空间位置曲线（hf=hlow）Fig.5 Position profile of boundary trajectory（hf=hlow）

图6 下边界轨迹的速度变化曲线（hf=hlow）Fig.6 Velocity profile of boundary trajectory（hf=hlow）

可达域边界轨迹的迎角变化曲线如图7 所示，可以看出：迎角都是在轨迹末段加速增加，且终端迎角都大于40°，表明飞机最终是以大迎角姿态栖落。

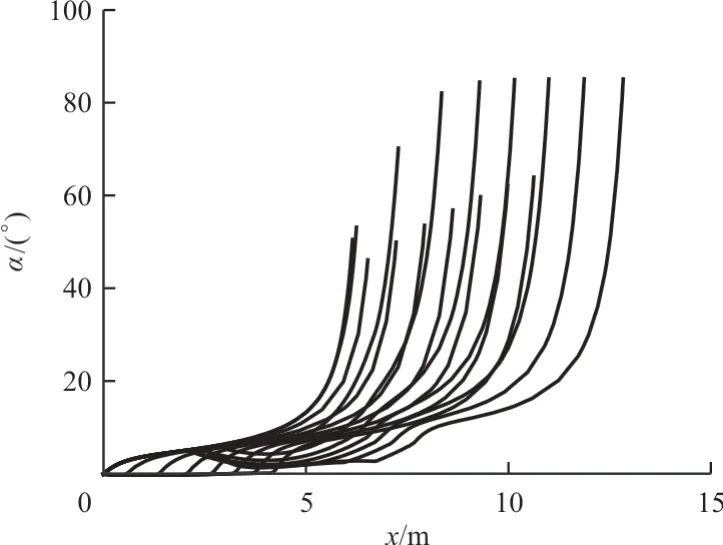
图7 迎角随水平位置的变化曲线（边界轨迹）Fig.7 Angle of attack profile of all boundary trajectories

可达域边界轨迹的俯仰角变化曲线如图8所示。

图8 俯仰角随水平位置的变化曲线（边界轨迹）Fig.8 Pitch angle profile of all boundary trajectories

栖落轨迹可达域计算结果如图9～图10 所示，可以看出：无动力飞行器纵向栖落轨迹可达域整体为上窄下宽的不对称区域，且左右边界曲线线性度较好；如果

h

取值更小，则可达域下边界会更宽。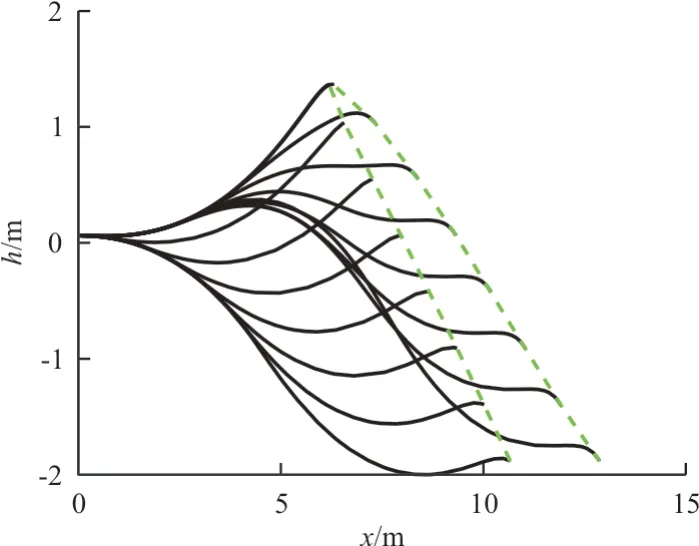

图9 边界轨迹的空间分布Fig.9 Boundary trajectories

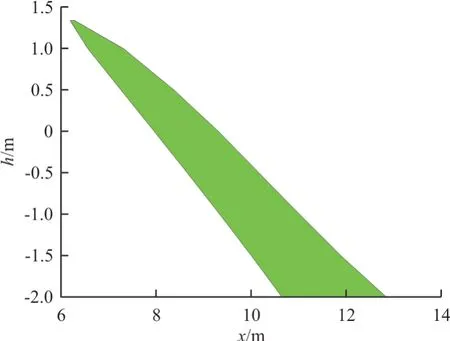
图10 可达域Fig.10 Reachable set

本文选取8 个高度离散点，总共需要计算16条边界轨迹，计算程序采用MATLAB 语言，在普通计算机上完成计算共耗时100 s。取点的密集度越大，计算耗时会相应增加，可达域也会更加精确。

4 结 论

本文将数学中的可达域概念引入到飞行器栖落机动任务中，给出纵向二维空间可达域的定义及其数学描述，建立其轨迹优化数值模型，并采用高斯伪谱法进行求解。在给定终端高度下边界的情况下，无动力飞行器纵向栖落轨迹可达域为上窄下宽的不对称区域，且左右边界曲线线性度较好。

栖落轨迹的可达域分析可以为着舰落区评估、方案筛选等着舰任务的总体设计提供参考。未来，可进一步开展栖落轨迹的可控域、栖落轨迹在线规划等研究。