电池储能提高电网薄弱节点电压稳定性的研究

曹鹏程，李培强，孙培栋，夏正邦

（福建工程学院信息科学与工程学院，福建 福州 350118）

由于煤、石油、天然气等化石燃料日趋紧缺，清洁能源在电力系统中的占比逐渐增大。电力系统中如果含有风电或光伏，其调压调频的能力会遭到削弱，因为风电和光伏多数是以最大功率点跟踪控制，系统在受到扰动时备用容量不足导致频率和电压波动难以平抑，影响系统稳定运行[1]。理论研究和实践证明，引入电池储能系统（battery energy storage system，BESS）可以有效提升间歇性可再生能源电源的运行性能与调控能力，有利于提高其接入电网的能力[2]。电池储能由功率转换装置（power conver⁃sion system，PCS）控制，响应速度快、控制精度高、能量效率大，可以双向控制有功无功，非常适用于调压调频[3]。

要研究储能并网对系统的影响，首先要研究储能系统的动态模型[4]。然而当前所进行的储能建模研究一般都是针对储能系统本身，研究储能元件的电量吸收释放特性[5]、控制系统的优化设计等[6]，其模型复杂精细，主要着眼于储能系统运行性能的提升。为研究储能系统对平抑电网扰动的影响，现在急需解决的问题是如何建立一个简化的储能机电暂态模型。文献[7]提出一种可以模拟电池、超导、超级电容储能的通用暂态模型，但仿真时仅分析了系统在大片云飘过导致光伏出力波动的暂态过程。文献[8-9]建立了储能系统的稳态模型和机电暂态模型，仿真验证了模型的有效性，但是模型中缺少死区，会导致储能系统充放电频繁，影响电池寿命。上述研究在储能系统的机电暂态模型中没有考虑储能参与有功调节的死区问题，会造成储能系统反复动作，没有考虑实际储能系统的容量限制，储能系统不能无限制地充放电。

针对电池储能系统在电网中的选址问题，目前研究成果已有很多。文献[10]在四机两区域系统中进行小干扰稳定分析，获得系统的特征向量和特征值灵敏度，以此选择储能的接入位置来抑制低频振荡。文献[11]在含有多个风电场的系统中采取灵敏度分析法和电气距离法融合的组合优化算法，得出储能系统的最佳接入节点。文献[12]采用向量场正规形理论，以节点电压线性和非线性参与因子为依据，得出系统在轻载和重载时最能提高电压稳定性的节点。以上文献的特点是在PSASP中建立储能或者FACTS装置的模型，然后用灵敏度分析法或者参与因子法，确定系统中储能的接入节点。

本文在对电池储能系统和PCS的结构深入研究的基础上，在PSASP中提出了考虑储能有功调节死区和无功功率限制的机电暂态模型，利用用户自定义（user-defined，UD）建模功能，基于节点电流注入法建立模型并网接口。并通过对CE⁃PRI-36节点系统进行电压稳定计算，运用模态分析和灵敏度分析得出系统中的薄弱节点作为储能的接入位置。通过仿真分析验证了所建模型可以改善薄弱节点电压稳定性，同时验证了所建模型接入薄弱节点较接入其他节点在维持电压稳定方面具有优越性。

1 BESS的暂态模型

1.1 BESS的暂态数学模型

BESS的组成结构主要有蓄电池组、并网换流器PCS及数据监测与控制系统，如图1所示。蓄电池组经过并网变流器与电网进行能量交换。

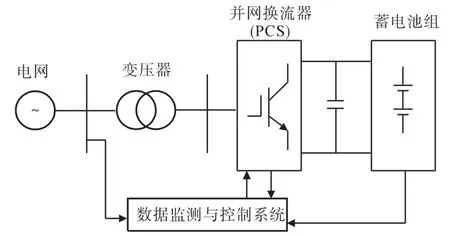
图1 BESS结构Fig.1 The structure of BESS

本文在图1的基础上建立电池储能系统机电暂态模型，图2是其结构图。其中储能电池模型可以简化在换流器充放电功率限制中。并网换流器采用内外环控制策略，通过比例积分控制调节系统偏差，电网接口模型将有功和无功转换成交流电网注入电流的实部与虚部，进而对电网参数进行控制。图2中，Pset，Qset为有功、无功功率控制指令；P，Q为BESS预期输出的有功、无功功率；IR，II为BESS注入电网电流的实部和虚部。

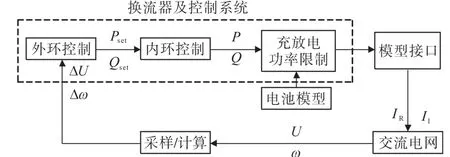
图2 电池储能系统模型结构Fig.2 The model structure diagram of BESS

电池储能系统接入电网的端口特性与PCS控制方法的联系是非常紧密的。换流器的控制策略通常可分成外环和内环两部分[13]。外环控制为有功无功控制，根据系统偏差量产生功率的调节量；内环控制为电压电流控制，产生脉冲宽度调制（pulse width modulation，PWM）信号，控制BESS的有功与无功功率输出，变换器控制框图如图3所示。图中：Δω，ΔU分别为频率和电压偏差量；m，δ分别为PWM调制信号和触发角控制信号。

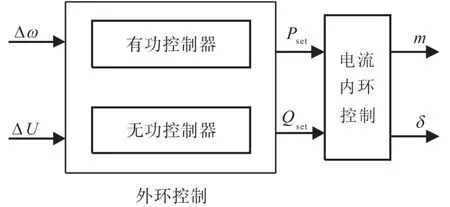
图3 变换器控制框图Fig.3 The block diagram of converter's control strategy

1.1.1 外环控制器设计

在电力系统中有功功率的变化会引起频率的波动，无功的变化引起电压的波动，所以换流器的外环控制采用频率/有功控制和电压/无功控制，输入量是电网频率和电压的实测值与控制目标预设值之间的偏差量，输出量是有功与无功控制量，以此再作为内环控制器的输入量。外环控制器的框图如图4所示，频率、电压偏差量经比例积分控制产生有功/无功输出控制指令。

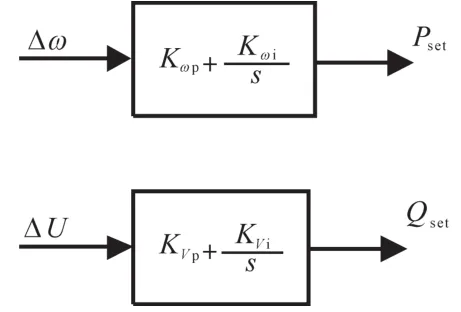
图4 外环控制框图Fig.4 The block diagram of outer loop control

由图4可知：

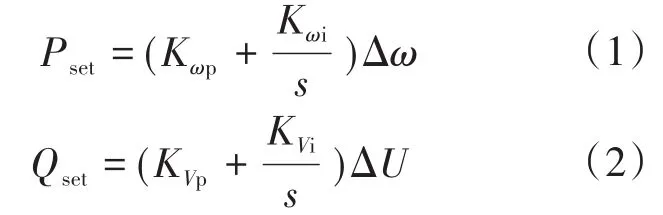
式中：Kωp，Kωi分别为频率/有功控制的比例和积分系数；KVp，KVi分别为电压/无功控制的比例和积分系数。

1.1.2 内环控制器设计

电流内环选择有功与无功的解耦控制。图5为储能系统的并网结构图。U∠θ为变换器交流侧电压向量；Ut∠θ为电网侧电压向量。d，q轴的电压电流关系为

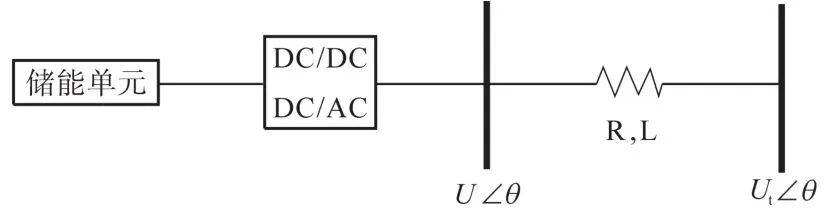
图5 储能并网示意图Fig.5 Schematic diagram for the integrating of power storage system

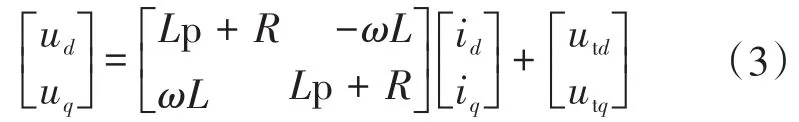
式中：ud，uq分别为U∠θ的d，q轴分量；utd，utq分别为Ut∠θ的d，q轴分量；id，iq分别为变换器交流侧电流i的d，q轴分量；p为微分算子。

储能系统交流侧P和Q分别为

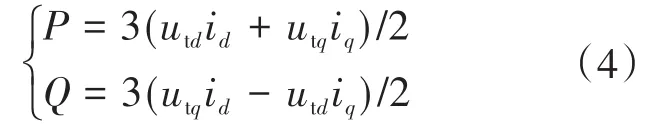
将电网侧电压向量与d-q坐标系的d轴重合，则U∠θ的q轴分量uq为零，P，Q可表示为

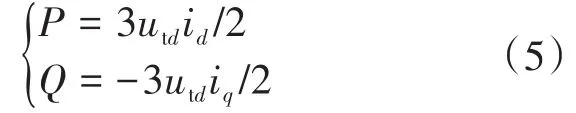
由式（5）可以看出，P和Q因为d，q轴变量相互耦合，所以很难独立控制。采用前馈解耦控制[14]，电流调节器经PI控制，则Ud，Uq的控制方程为

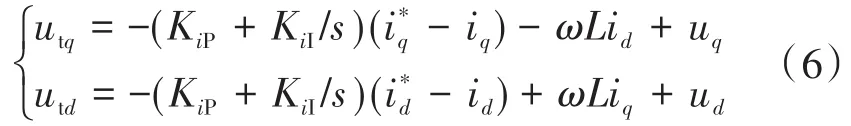
式中：KiP，KiI分别为PI调节的比例系数和积分系数；分别为注入电流向量的d，q轴分量。

把式（3）代入式（6）之后便可将电流解耦，控制方程为

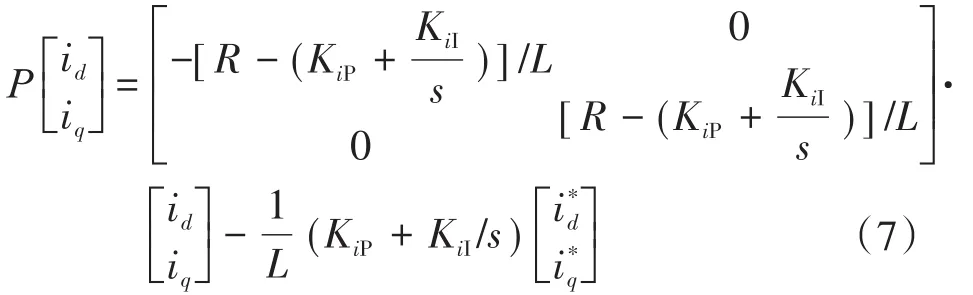
根据式（3）和式（6）建立带有前馈解耦控制的电流内环控制框图，如图6所示。

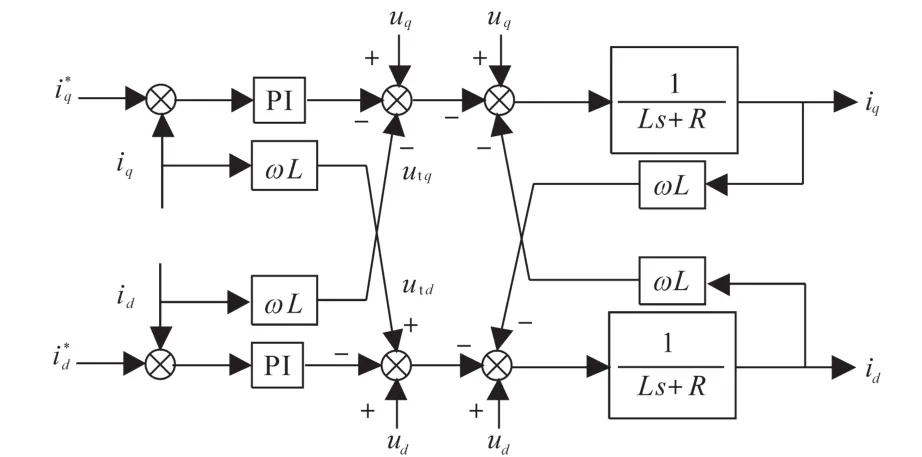
图6 加入前馈控制后电流输出框图Fig.6 The current output block diagram with feedforward

在图6的基础上进行等效变换得到图7。根据图7，可得iq电流内环闭环传递函数：

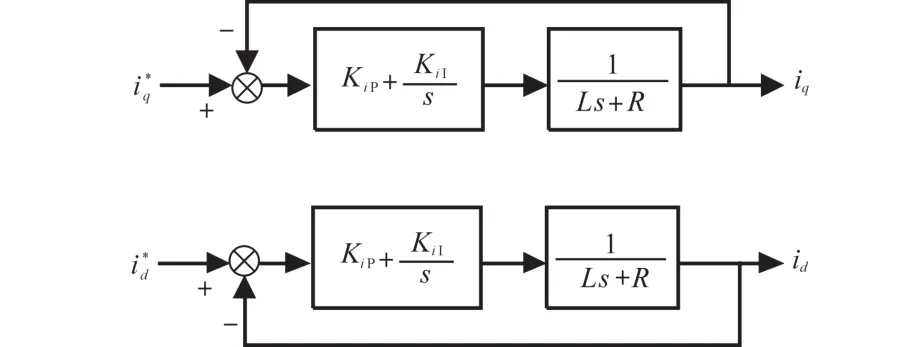
图7 化简后电流控制框图Fig.7 Simplified current control block diagram

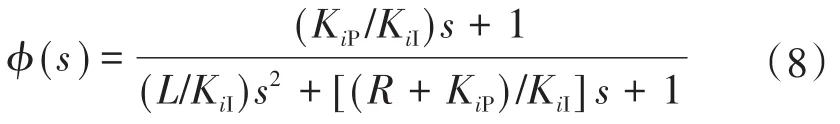
式（8）中有1个零点和2个极点。根据零极点对消的原则，式（8）还可以再简化，储能系统内环的功率调节特性可以近似等效为1阶惯性环节：

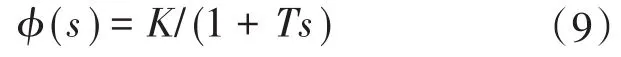
在储能系统的功率控制中，内环控制器可以简化为两个独立的1阶惯性环节。其功率特性为

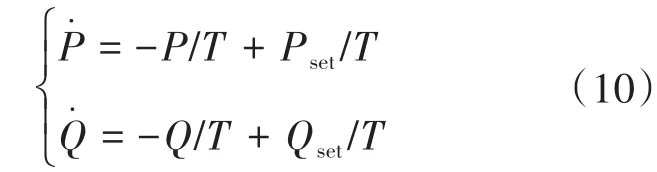
由式（10）可得内环控制框图如图8所示，Pset，Qset通过1阶惯性环节产生有功和无功功率。

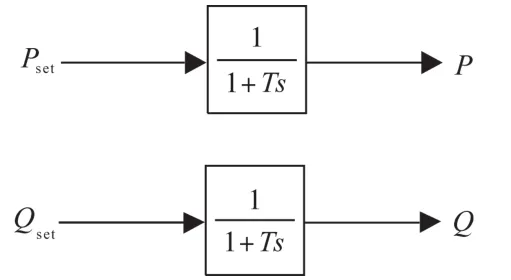
图8 内环等效控制框图Fig.8 The equivalent block diagram of inner loop control

1.2 储能系统的PSASP机电暂态模型

1.2.1 储能有功调节死区环节设计

在有功输出控制模块中，把死区环节加入到频率控制给定值与实测值的差值后面，如果差值Δf的绝对值在死区之外，就启动有功输出控制。图9为有功输出控制模块中的死区环节。

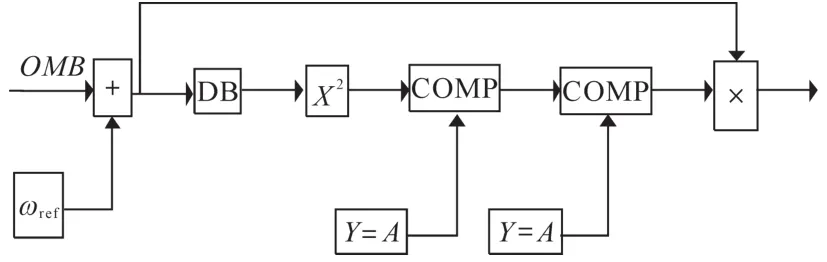
图9 有功控制模块中的死区环节Fig.9 Dead band segment in active power control module

图9中OMB为母线频率，与频率给定值ωref作差。DB为UD中自带的死区模块，但是其输出量是输入量与死区的差值，可能是正值、负值或者零值。所以从DB模块输出的值要平方，经过平方以后输出的值都为正值或0。后面的COMP是比较模块，设置成反相器，输入正值，输出是0；输入0，输出就是1。之后再加入一个比较模块，同样设置成反相器，将前面比较模块输出的0或1反相，这样就实现了将DB死区模块输出的值转变为1或者0。在最后加入一个乘法模块，一个输入为0或1，另一个输入值为Δf。如果Δf在死区范围内，则通过前面的各个模块输入到乘法模块的值为0，最终整个死区环节输出的值也为0；如果Δf超出了死区范围，则通过前面的各个模块输入到乘法模块的值为1，最终整个死区环节输出的值为Δf。

1.2.2 储能无功功率限制环节设计

在无功功率输出控制模块中，需要考虑逆变器容量对无功功率的限制。图10为无功控制模块中的逆变器容量限制环节。

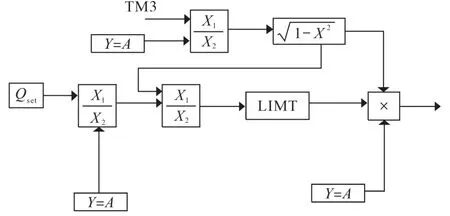
图10 无功控制模块中的逆变器容量限制环节Fig.10 The limitation segment of inverter capacity in reactive power control module

图10中TM3为有功参考控制功率Pset，所有的赋值环节都为逆变器容量S。根据公式S=P2+Q2，将Pset/S输入均方差根模块，输出的值就是Q/S，这里的Q是考虑了逆变器容量限制，通过计算得出的无功功率。Qset为无功参考控制功率，用Qset除以逆变器容量S，得出的值再去除以Q/S，这样就可以得出Qset/Q的值。Qset/Q输入到LIMT限值模块，模块中的参数Ymax设置为1，Ymin设置为0。如果0＜Qset/Q＜1，那么就输出Qset/Q本身。如果Qset/Q＞1，则输出1。LIMT模块输出的值再与均方差根模块输出的值Q/S相乘，再乘以S，最后输出的便是考虑逆变器容量限制之后的无功功率。

1.2.3 基于节点电流注入法的模型接口设计

PSASP中发电机、负荷、储能元件等都是以节点电流的形式注入电网[15]，所以参与暂稳计算的用户自定义模型接口必须是电流注入形式。因此储能系统输出的功率要转化为电流源电流实部和虚部的形式注入电网。

设S=P+jQ为储能系统在安装节点注入的视在功率，UR，UI为并网点母线电压U的实部、虚部，IR，II为注入电流I的实部、虚部，则

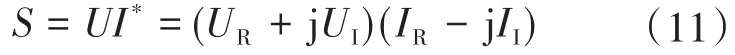
展开得到P，Q：

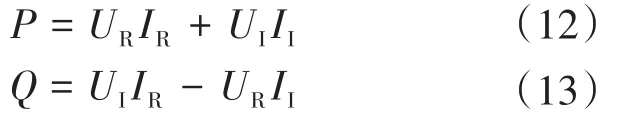
求解上述方程组，得：

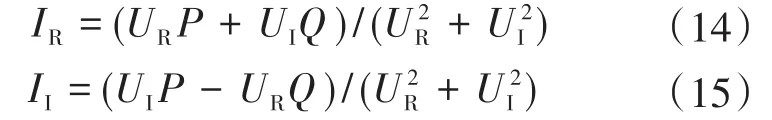
根据式（11）～式（15）可以搭建BESS机电暂态仿真模型的接口部分，如图11所示。

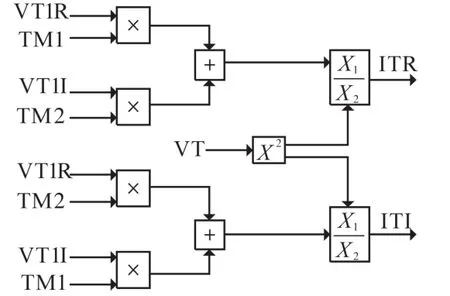
图11 模型接口部分Fig.11 Model interface part

本文利用电力系统分析综合程序PSASP7.0中的用户自定义建模功能构建BESS的机电暂态仿真模型，各模块模型结构如图12所示。其中VT为母线电压；VT1R，VT1I为电网电压的实部和虚部；ITR，ITI为储能系统向电网注入电流的实部和虚部；TM1，TM2分别为储能系统有功和无功输出，框图的具体含义参见文献[15]。

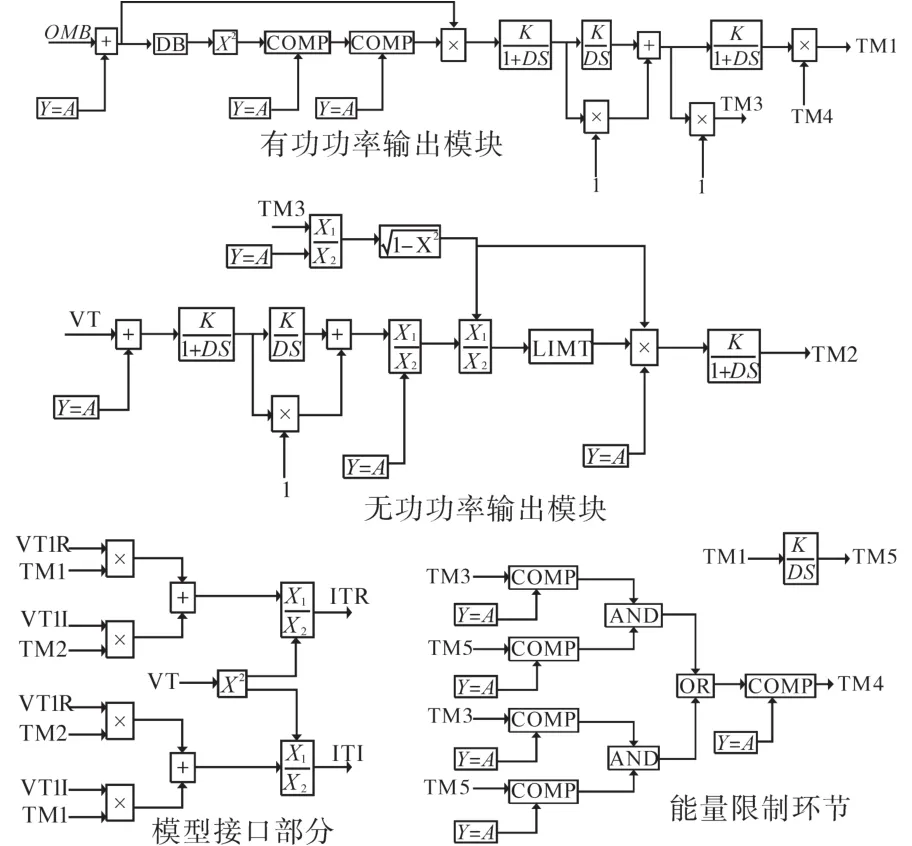
图12 PSASP储能模型Fig.12 Model of the power storage system on PSASP

2 电网薄弱环节的确定

2.1 用模态分析法筛选系统薄弱节点

运用模态分析方法判定系统的电压稳定性，主要是识别出系统的潮流雅可比矩阵JS的特征值和对应的特征向量。在常规潮流雅可比矩阵的基础上将发电机、负荷静态化后可以得到修正后的电力系统潮流方程为

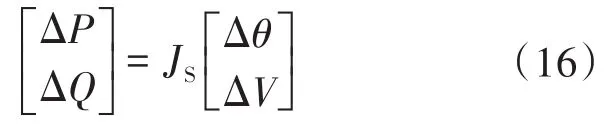
因为电压的变化主要与无功功率有关，所以令ΔP=0，则系统负荷无功和节点电压的关系为

对JR作特征值分解可得：

令λ-1=ξ，可得：

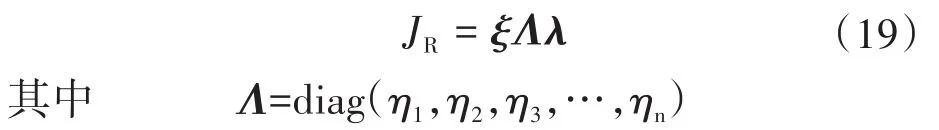
式中：η1，η2，η3，…，ηn为JR的特征值；ξ为JR的左特征向量阵；λ为JR的右特征向量阵。

将式（19）代入式（18），得：

由式（20）可得：

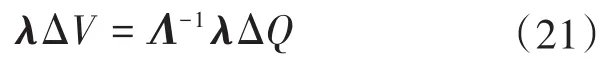
令λΔV=Δv，λΔQ=Δq，则有

式中：Δv，Δq分别为模态电压v和模态无功q的变化量。

由式（22）得第i个模式为

当ηi的值很小或约等于零时，反映出模态电压会因为模态无功的微小变化而发生巨大变化，所以系统具有不稳定的趋势。

为了判别系统的关键节点和区域，定义了母线参与因子：

式中：ξki表示在母线k右特征向量阵ξ的第i列的影响；λik表示在母线k左特征向量阵λ的第i行的影响；pki表明ηi在母线k对电压/无功灵敏度的影响。先找出JR最小的特征值及与其相关的母线参与因子。对各节点的参与因子排序，参与因子越小，说明节点越稳定；参与因子越大，说明节点越薄弱。

2.2 用灵敏度分析法筛选系统薄弱节点

灵敏度分析可以表述出系统状态变量或输出变量对系统参数或控制条件变化的敏感程度。运用灵敏度分析法可以将电力系统中诸多物理量对系统状态的影响程度表述出来[16]。

通常情况下，电力系统的数学模型可以用一组非线性方程来描述：

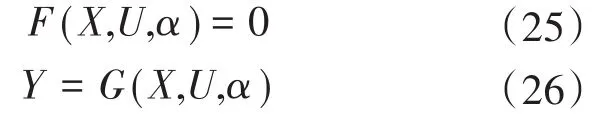
式中：X为状态变量，如电压VL、角度δL，δg等；U为控制变量，如有功功率Pg、电压Vg，V0和相角δ0等；α为参数，如线路的导纳G，B等。上述变量的下标“L”，“g”，“0”分别对应的是PQ节点、PV节点和平衡节点的量。

忽略控制变量之间的作用关系后对式（25）式、（26）中的控制变量U进行全微分，得到：

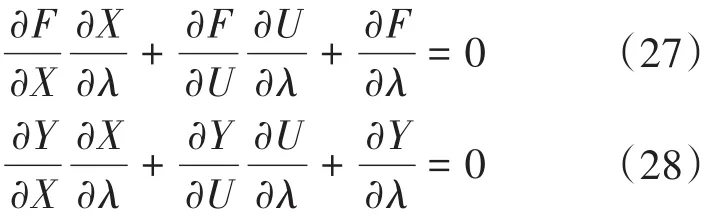
故可得出X和U的参数灵敏度分别为

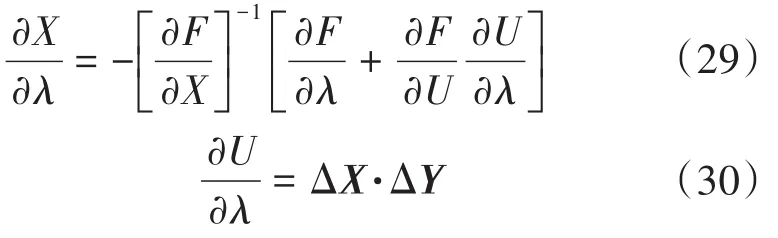
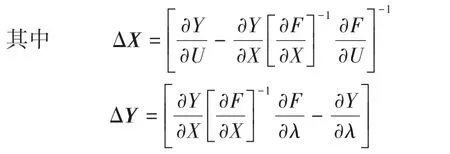
由式（17）、式（18）能计算出系统状态变量和控制变量对主要参量的敏感程度。灵敏度法的实质是把系统向负荷输送功率的极限状态当作电压稳定临界点，用临界时不同灵敏度作为判定指标。选择某灵敏度指标，计算各节点灵敏度值并排序，薄弱节点就是最大或最小灵敏度对应的节点。

3 算例分析

3.1 PSASP电压稳定模块确定系统薄弱节点

本文在PSASP仿真平台，选取中国电科院36节点（CEPRI-36）标准算例，采用灵敏度分析法和模态分析法确定系统关键节点。系统基准容量为100 MV·A，单线图如图13所示。

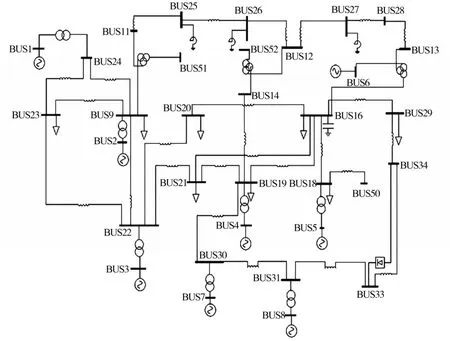
图13 CEPRI-36节点系统单线图Fig.13 CEPRI-36 system single line diagram

负荷、发电机的静态特性与电压稳定性密切相关，在进行电压稳定计算时，负荷模型为恒阻抗模型和恒阻抗感应电动机混合模型，混合比例为1∶1。图14和图15分别为电压稳定计算得出的灵敏度和参与因子数据折线图。

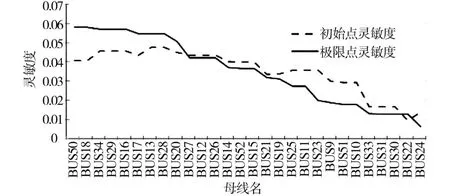
图14 电压稳定计算初始点和极限点的灵敏度Fig.14 Sensitivity of initial point and limit point of voltage stability calculation

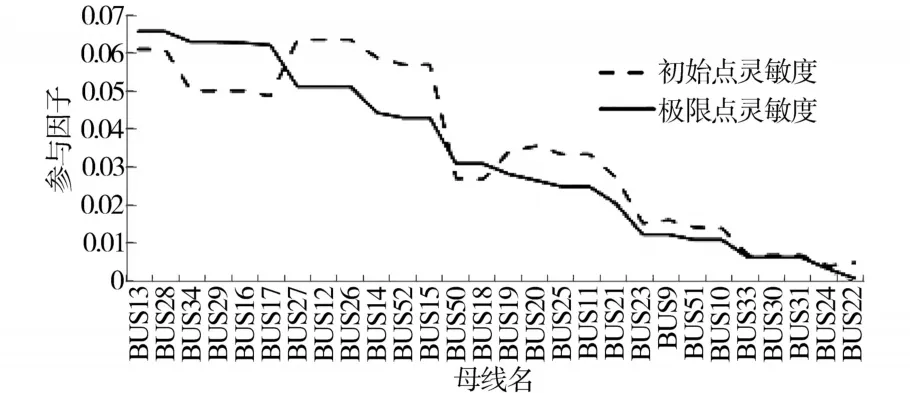
图15 电压稳定计算初始点和极限点的参与因子Fig.15 Participation factors of initial point and limit point in voltage stability calculation

表1和表2为各节点在初始点与极限点的灵敏度和参与因子。

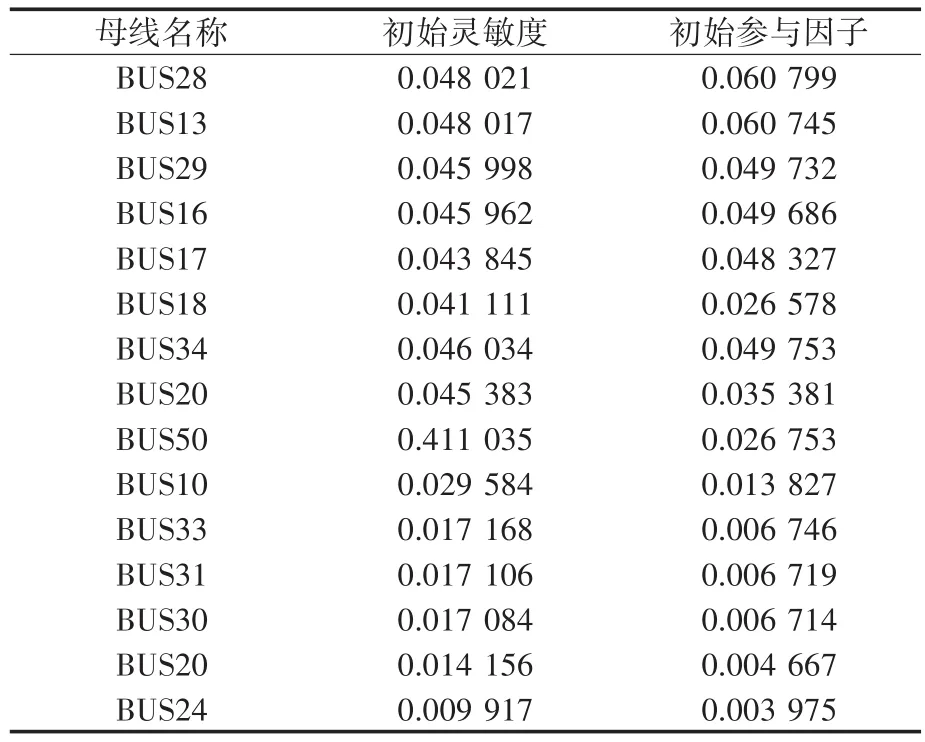
表1 电压稳定初始点的灵敏度与参与因子Tab.1 Sensitivity and participation factors of initial points in voltage stability

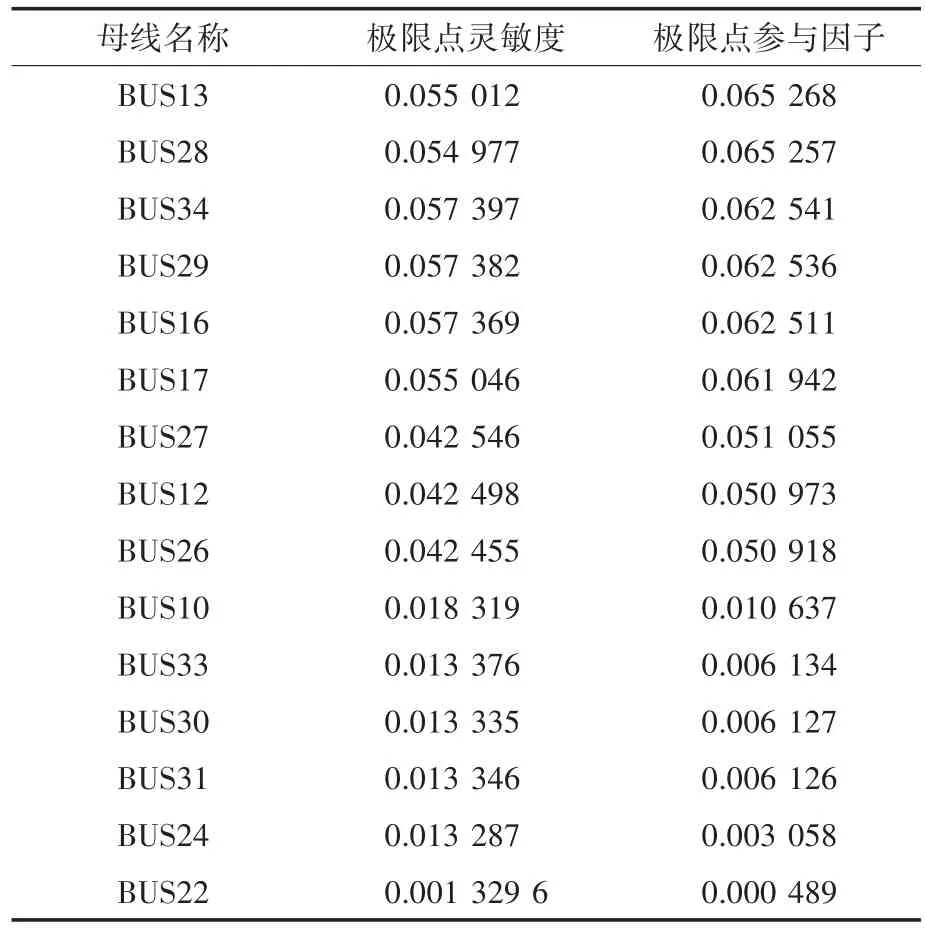
表2 电压稳定极限点的灵敏度与参与因子Tab.2 Sensitivity and participation factors of limit points in voltage stability

结合图14、图15和表1、表2可知，CEPRI-36节点系统中13，28，34，29，16和17节点为灵敏度和参与因子都较高的节点，构成的区域就是电压稳定比较薄弱区域。综合考虑，选择BUS16为电池储能系统的接入位置。

3.2 电池储能改善电压稳定性的仿真分析

将所建立的电池储能模型接入BUS16节点，然后设置系统故障为0.2 s时BUS29母线上连接的负荷切除30%，设置储能有功出力为0.75（标幺值），观察储能接入节点BUS16的电压波动变化，与储能未接入时的电压波形做比较，如图16所示。

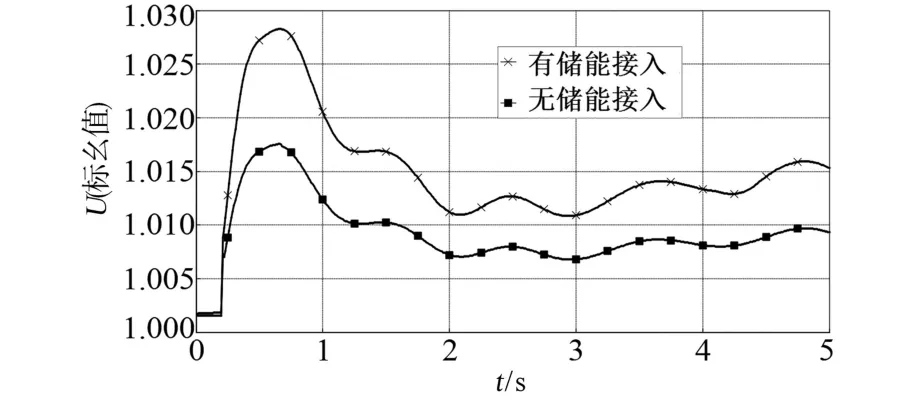
图16 有无储能接入的电压波形比较Fig.16 Comparison of voltage waveforms with or without energy storage

图17为发电机G6与G5之间的功角变化。

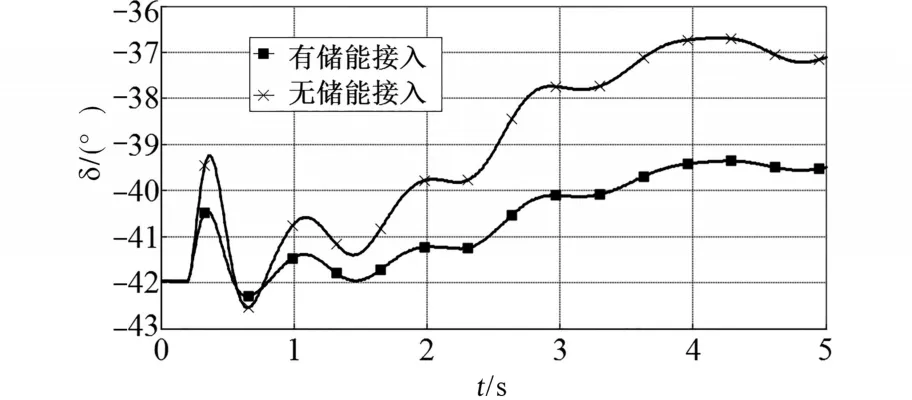
图17 有无储能接入的发电机功角变化Fig.17 Change of generator power angle with or without energy storage

从图16中可以看出，在系统发生切负荷的扰动时，储能没有参与调节的情况下，BUS16的母线电压达到了1.018（标幺值），峰谷最大差值为0.026 5（标幺值）。当BUS16上接入电池储能系统时，母线电压的最大值为1.006（标幺值），峰谷最大差值为0.014（标幺值）。而且储能接入后，电压的波动幅度明显变小，可以很快趋于稳定。从图17中可以看出，储能接入后发电机功角第一摆时的幅值减小，后续波动的幅度变小，稳定性大大提高。

仿真结果验证了该模型的有效性，证明该模型可以改善薄弱点电压稳定性。

3.3 电池储能模型不同接入位置的仿真分析

综合比较3.1节中各节点的灵敏度和参与因子，可以看出BUS24为系统中灵敏度和参与因子都较低的节点。

系统故障的设置与3.2节一样，将电池储能系统分别接入BUS16和BUS24，设置储能有功出力为0.75（标幺值），观察所切负荷的母线BUS29的电压变化，波形如图18所示。

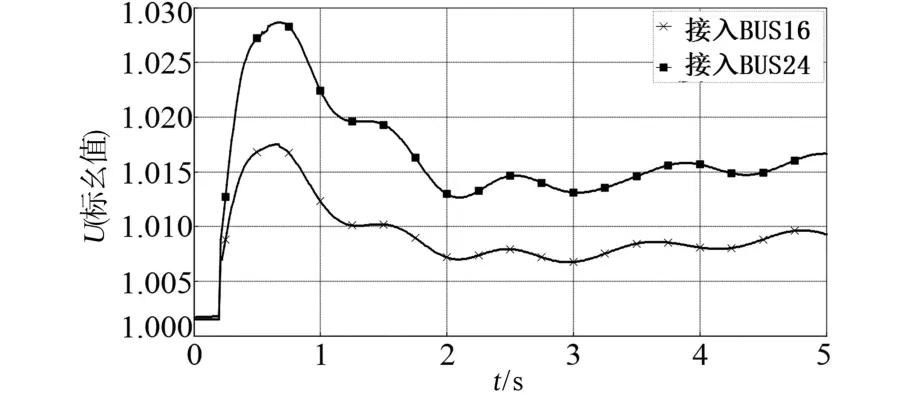
图18 储能不同接入位置的电压变化Fig.18 Voltage variation of different access positions of energy storage

由图18可知，在同样的系统扰动下，电池储能系统接入薄弱节点BUS16对扰动的平抑效果要比接入BUS24好很多。BUS29发生切负荷后，电池储能接入BUS24的情况下，BUS29的电压波动最大幅值为1.017（标幺值），峰谷最大差值为0.024（标幺值）。相同故障，电池储能接入BUS16的情况下，BUS29的电压波动最大幅值为1.006（标幺值），峰谷最大差值为0.014（标幺值）。从波形和数据上可以看出，选择BUS16作为电池储能系统接入电网的节点，对改善电网运行波动的效果较好。

4 结论

本文以BESS各部分设计原理为基础，在PSASP的用户自定义建模中搭建了可以体现储能有功调节死区限制、充放电功率限制、逆变器容量限制等储能特性的BESS机电暂态模型。利用PSASP的电压稳定计算功能对CEPRI-36节点系统进行了模态分析和灵敏度分析，确定了系统中的电压薄弱区域，作为BESS的接入位置。

本文仿真分析了系统发生负荷切除的情况，结果显示储能系统可以很好地改善薄弱节点的电压稳定性，并且储能模型接入电压薄弱节点对抑制母线电压波动的效果较接入其他节点时要好很多。