基于FIMD和Hilbert变换的线路行波故障诊断

盖志强，洪卫东，张华峰

（国网山西省电力公司长治供电公司，山西 长治 046000）

随着我国电网技术的迅猛发展，系统电压等级越来越高，各种大容量以及长距离的输电线路也越来越多，电力系统的规模也越来越大。在大规模的电力系统中，高压输电线路是其重要组成部分，因此高压输电线的稳定性对电力系统的稳定运行起着十分重要的作用。一旦高压输电线路出现故障会对电力系统产生较大的危害，其中电力系统连锁事故多是由于没有及时排除和查找线路故障所引发[1]。因此，采取快速有效的方法进行线路行波故障诊断成为当前研究的热点话题，而快速、准确实现线路行波故障诊断不仅能够降低线路故障查找工作的强度，同时也能够及时解决故障，提升电网运行的安全性，确保电网的稳定运行。

最近几年以来，国内外大量文献资料针对线路行波故障诊断进行了大量的研究。文献[2]结合某省电力公司历史污闪故障，分析绝缘子污闪影响因子，以行波测距原理为基础，结合在线监测、历史故障库等多源信息，通过污闪故障影响因素组建绝缘子污闪诊断模型，分析故障影响概率，最终根据组建模型的结构实现故障诊断。文献[3]采用相模态分解获取故障反向行波，在此基础上对反向行波进行小波模极大值变换，提取极大值突变时刻以及对应极性，利用该原理选择满足时差、波速与线路长度关系的有效时差。在此基础上将所有提取到的极性信息作为神经网络输入，并对神经网络的输出误差进行调整，在误差最小化的情况下实现故障距离计算，得到故障诊断结果。文献[4]主要采用参数交替优化的变分模态分解（variational modal decomp，VMD）算法获取更为合理的信号分解过程中的k值和α值。在此基础上，利用Teager能量算子的多种优势将该方法应用于高压输电线路故障行波检测过程中，并以此为基础设计了一种不受波速和线路弧垂影响的输电线路双端故障行波测距的新算法，获取更为精准的定位结果。文献[5]通过分析行波幅值衰减特征与反射规律，对输电线路的临界故障距离进行单端测距，根据单端测距原理在线路中间布置额外测点，根据测点行波极性对输电线路故障区段进行定位，在该区域采用单端与双端相结合的方法实现故障定位。

以上方法虽然取得了较为满意的研究成果，但是由于在应用过程中，未能考虑到要对线路行波信号进行分解与频谱分析，导致故障诊断延时增加和精度下降，故障诊断费用上升。为此，提出基于快速本征模态分解算法（fast intrinsic mode decomposition，FIMD）和希尔伯特（Hilbert）变换的线路行波故障诊断方法，通过FIMD方法对线路行波信号进行分解。根据信号分解结果采用Hilbert变换进行线路行波信号频谱分析，获取信号的瞬时频率，通过瞬时频率计算行波到达的准确时间，从而实现线路行波故障诊断。

1 线路行波故障诊断

1.1 基于FIMD算法的行波线路信号分解

如果高压输电线路在某位置发生了故障，此时需要利用叠加定理对故障状态进行分析，得到等值电路。由叠加定理可知，故障后各个附件的等效电源方向相反，但大小相同。在附加电源的作用下，会分别在故障点的两端形成电压行波和电流行波。

高压输电线中的行波波速和基本参数之间存在一定的关联，如果三相输电电路之间具有耦合关系，则无法精确计算行波波速。所以通过解耦的方法确定行波波速，具体是采用相模变换方法将相互耦合的分量变换为具有相互独立的模态分量，进而更好地实现解耦。相对电压互感器而言，由于采用电流互感器能够更好地实现完成高频分量传输，因此直接通过电流对故障距离进行测量。以下采用凯伦贝尔相模变换可以将相电流划分为以下的形式：

式中：im为相电流分量矩阵；i为模电流分量矩阵；Q为变换矩阵；i0为零模分量；iα，iβ分别为α模和β模分量；ia，ib，ic分别为不同的独立模电流分量。

α模和β模分量的计算公式表示为

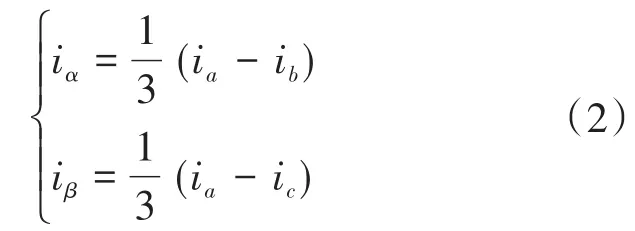
通过上述变换，针对测量的无损三相位输电线路而言，能够获取对应的模波速计算式如下式所示：

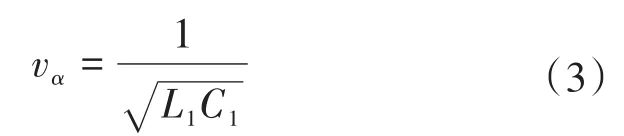
式中：L1为输电线路的正序电感；C1为输电线路的正序电容[6]。

结合上述分析可知，针对不同类型的故障，能够选取不同模的电流进行故障定位分析。

FIMD算法可以对非平稳信号进行自适应分解，但为了有效消除模态混叠现象，需要将初始线路行波信号划分为一个固有模态分量且具有唯一的计算结果。针对于传统的经验模态分解算法（empirical mode decomposition，EMD）而言，FIMD算法不仅具有较高的运行效率和较好的收敛性能[7]，同时具有超强的信号分解能力以及较快的计算速度。以下给出FIMD算法的具体实现过程：

1）设定输入的信号为f(t)，对信号对应的极值点R(t)进行计算（t表示采样时刻），则存在t0≤tj≤tm-1，m代表分析信号极值点的数量，t0，tj，tm-1分别代表不同的采样时刻。

2）通过线性转换方法将全部极值点进行转换，形成残余量r(t)，具体的计算式为

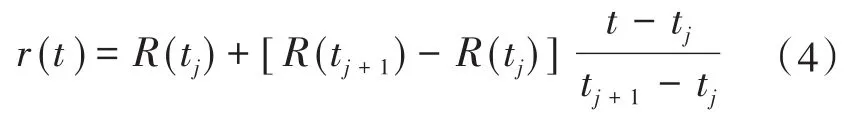
式中：tj+1为第（j+1）个极值点对应的采样时间。

3）令初始的输入信号减去剩余的残余量，获取输入信号固有的模态函数，具体操作流程如下所示：①将固有模态函数的第i个极值点E(ti)设定为修正控制点，设定控制点的坐标为Pi，则可以表示为Pi(ti,E(ti))；其中ti为极值点i对应的采样时间。②对第i个向量的乘积进行定义，具体的计算式为

③对上述操作过程进行迭代，当残余量的极值点不超过3个时，则能够结束上述分解过程。④根据上述计算过程，可以将初始的输入信号划分为多个含有唯一解的固有模态分量和残余分量[8]。

综合上述分析可知，初始信号经过FIMD算法分解之后，能够获取多个唯一的固有模态分量和一个残余分量。

1.2 基于Hilbert变换的线路行波故障诊断

Hilbert变换是一种独特的完全自适应时频分析方法，主要用于非线性以及非平稳信号的处理，同时也适用于线性以及平稳信号的处理，和其他时频分析方法相比，Hilbert变换能够更好地反映信号的物理意义。

Hilbert变换的核心部分为FIMD算法，FIMD算法是将一个非平稳信号转换为多个平稳信号的过程，同时取多个唯一的固有模态分量和一个残余分量[9]。根据信号结果进行Hilbert变换，获取随时间变化的瞬时频率以及瞬时幅值，能够获取信号的时间—频率—能量分布，即通过Hilbert频谱能够更好地反映信号瞬时频率和瞬时振幅，其中两者皆为时间函数。通过时间—频率—振幅组成信号的Hilbert频谱的具体操作过程如下所示：

设定某一实信号为Y(t)，则其对应的Hilbert变换为

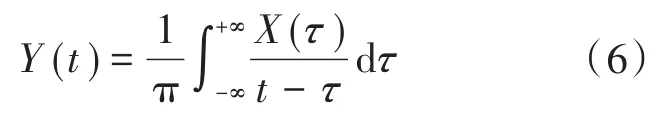
其对应的反变换表示为

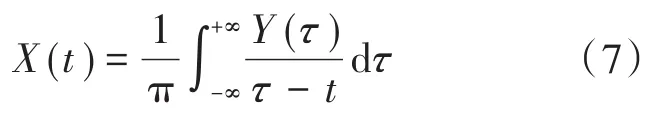
其中Y(t)和X(t)两者能够形成复共轭，组建的解析信号能够表示为

式中：a(t)为信号瞬时振幅；θ(t)为信号相位。则有：

瞬时速率的表达式为

通过式（10）可知，k(t)为时间的单值函数，即任意时间对应的任意频率。为了使任意时间对应的频率更加有意义，需要通过Hilbert变换将时间序列转换为单组分[10]，而FIMD算法恰好能够满足这一要求。

固有模态分量中包含数据的振荡模态，通常情况下，固有模态分量需要满足以下的约束条件：

1）在数据长度上，信号极值点的数量和过零点的数量一致或者最多相差1个。

2）在随机点集中，由局部极大值点组建的包络线和局部极小值点组建的包络线取值为0。

一般一个随机给定的时间点可能含有多个振荡模态，且大部分的信号无法满足固有模态分量的约束条件，此时则需要通过FIMD算法将复杂的信号进行分解，获取对应的固有模态分量[11-12]。

在输电线路运行过程中，相同杆塔上的输电导线实际上相互之间能够组成一个含有电磁耦合效应的分布式参数系统，各种电压以及电流是因电磁耦合效应存在的，并不是相互独立的理想状态。其中两个模态分量是由α模和β模分量组成的，通过单根导线的波动方程对不同的分量进行计算：

将式（11）分别代入三相电压A，B，C之后，获取相应的模分量，能够将其表示为

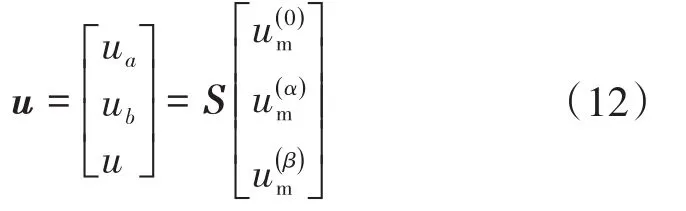
由于行波到达各个母线的故障点时间之间存在关联，通过这个关系能够将母线和故障点位置反映过来的波头时刻进行区分，进而获取位置、时间以及波速三者之间的关系。

基于Hilbert变换的线路行波故障诊断是通过时频图中频率突变点检测行波到达测量点的距离，由于经过FIMD算法分解和Hilbert变换获取的瞬时频率均为正值，所以通过Hilbert变换无法判定反射波头的极性，而波速测距法主要通过判断波头极性辨识方法选取母线的透射波以及故障点反射波进行测距，但是Hilbert变换和单端测距法两者的组合无法实现故障测距，所以本文主要使用了双端测距算法。

波速是测距精度的决定因素之一，在实际运行过程中波速大小主要取决于架空线的结构以及大地电阻的分布，故障定位实现步骤如下：

1）0模分量是以大地为回路，因此会有较大的衰减以及波速不确定性，频率变化对0模也有较大程度的干扰，所以0模行波十分容易和其他模量相互混杂重叠，稳定性极差[13]。在不考虑线路参数频率相关性时，α，β保持稳定和接近光速的波速，通过波速以及线路参数关系能够计算得到：

2）当启动行波测距系统时，通过仪器设备计算实际路线的传输速率是提升故障定位的有效手段。基于Hilbert变换的线路行波故障诊断分为以下几个步骤：①在线路两端变电站获取故障前一周期和后一周期母线测量端的行波电流数据[14-16]，将故障后一周期减去故障前一周期的行波分量值，则能够获取故障分量，使用FIMD进行信号分解，获取固有模态分量。②当分析不同模分量之间的相互影响时，通过故障识别算法判断出不同故障的类型，同时对具有代表性的模分量进行分析。最后，在不考虑模分量间相互影响的情况下，将线模分量作为主要的研究对象。③对两端电流行波的模分量进行分解时，通过最高频率分量获取时间—瞬时频率谱。④求解时间—瞬时频率谱的极大值，分别标定第一个模极大值到两侧母线测量端的时间。⑤将两端母线测量端的时间代入到双端测距公式，获取故障发生的位置，同时利用瞬时频率准确计算行波到达时刻，进而实现线路行波故障诊断。

2 仿真实验分析

为了验证所提基于FIMD算法和Hilbert变换的线路行波故障诊断方法的综合有效性，需要进行仿真实验设计。本文主要是通过PSCAD/EMT⁃DC搭建某地500 kV高压输电线路仿真模型，以输电线路仿真模型为基础对不同类型的短路故障及其电磁暂态过程进行模拟与分析。其中仿真实验参数设置如下：线路长度250 km，仿真时间60 ms，电源电压610.2 kV，单位长度的正序电阻0.026 Ω，单位长度的零序电阻0.185 8 Ω，单位长度的正序电感0.857 4 mH，单位长度的零序电感2.179 mH，单位长度的正序电容0.012 8 μF，单位长度的零序电容0.01 μF。

2.1 故障定位精度

本文主要将在仿真环境中对单相接地短路故障进行定位作为研究案例，设置第30 ms时距离左端80 km的位置发生单相接地短路故障。在此基础上获取该故障发生时的α模电流，对该结果进行解耦处理，最终得到1/4周期的α模电流，具体如图1所示。

图1 故障行波α模电流Fig.1 Fault traveling wave α-mode current

以文献[2]方法、文献[3]方法与本文方法作对比，对不同故障采用不同方法下的故障定位结果进行分析，结果如表1所示。

表1 线路行波故障定位精度对比结果Tab.1 Comparison results of line traveling wave fault location accuracy

由表1的结果可知，本文方法能够更快精确地测量出输电线路故障行波的到达时间以及故障距离，相对于文献[2]方法和文献[3]方法定位精度更高。主要是由于本文方法所提的FIMD方法对α模电流进行分解，所以具有较高的诊断精度。其中故障行波的分解结果如图2所示。

图2 FIMD方法的分解结果Fig.2 Decomposition results of FIMD method

分析上述结果可知，α模电流分解后可获得3个固有模态分量和1个残余量，在所有分量中，固有模态分量的频率较高，且而第246个采样点处α模电流开始波动。所以FIMD方法具备了计算量小以及计算结果更为精准的多种优势。

以固有模态分量1为基础，本文主要对其进行Hilbert变换，得到其瞬时频率图如图3所示。

图3 固有模态分量瞬时频率Fig.3 Instantaneous frequency of natural modal components

分析上述结果可知，第一个脉冲为初始行波，所对应的时间为10.628 ms，利用故障行波传输时间对行波波速进行计算，其结果为2.921 8 m/s，利用该结果对故障点进行定位，以期输出更为精准的定位结果。

2.2 线路行波故障诊断延时

当线路行波发生故障时，如果不及时进行诊断，会导致线路行波故障诊断延时增加，对整个输电线路产生不可估计的影响。以下实验测试将线路行波故障诊断延时作为测试指标，选取文献[2]方法和文献[3]方法作为对比方法进行测试，具体实验对比结果如表2所示。

表2 线路行波故障诊断延时对比结果Tab.2 Comparison results of line traveling wave fault diagnosis delay time

分析表2中的实验数据可知，由于故障类型的不同，使各个方法的线路行波故障诊断延时也在不断发生变化，其中本文方法的线路行波故障诊断延时明显更低一些，原因在于本文方法采用Hilbert变换进行频谱分析，有效简化了故障诊断流程，有效降低了诊断延时。

2.3 线路行波故障诊断费用

为了更进一步验证本文方法的有效性，针对不同故障类型下的不同行波故障诊断方法的费用进行分析，具体实验对比结果如表3所示。通过表3中的实验数据可知，故障类型的不同导致各个方法的线路行波故障诊断费用也存在十分明显的差异。其中本文方法由于在故障诊断过程中同时引入了FIMD和Hilbert变换方法，有效实现了信号分解以及频谱分析，全面改善了传统方法存在的弊端，促使整个方法的综合性能得到有效提升，因此使得线路行波故障诊断费用下降，全面验证了本文方法的优越性。

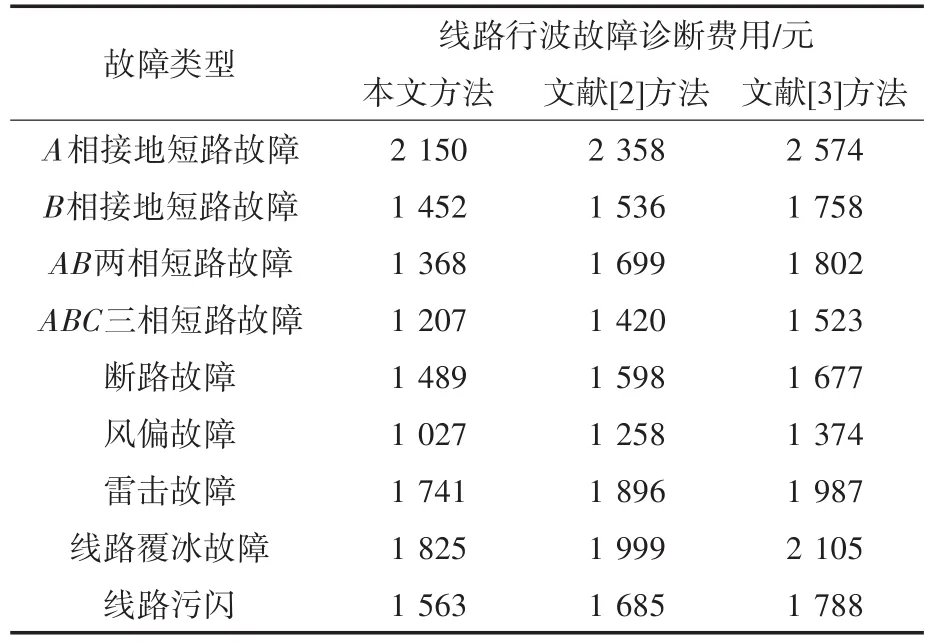
表3 线路行波故障诊断费用对比结果Tab.3 Comparison results of line traveling wave fault diagnosis cost

3 结论

为了更好地实现线路行波故障诊断，本文提出一种基于FIMD算法和Hilbert变换的线路行波故障诊断方法。仿真实验结果表明，本文方法能够在有效提升线路行波故障诊断精度的同时，大幅度减少故障延时与诊断费用。为了更进一步提升线路行波故障诊断的可靠性，后续将重点针对以下几方面的内容进行研究：

1）在实际应用的过程中，输电线路在发生故障时会产生噪声，但是本文方法未针对该方面的内容进行研究，后续将展开该方面的研究。

2）由于线路行波发生故障是十分复杂的，后续将全面利用故障信息，结合多种方法以提升故障诊断结果的准确性。