基于广义似然比检验算法的IM定子故障诊断

郭丽娜，张桂香

（郑州铁路职业技术学院电气工程学院，河南 郑州 454000）

感应电机（induction motor，IM）由于成本低、性能优良被广泛应用于各类工业场景中[1]。尽管IM可靠性较高，但随着使用年限的增加，其仍会出现多种故障[2]。因为定子绕组绝缘劣化可导致定子故障[3]，若得不到有效规避，则可能导致更为严重的后果，故必须开发IM的主动监控算法，以在早期检测IM绕组不平衡，以提高系统可靠性。

IM的状态监测方案种类较多[4-5]，但这些方法大部分需要改变系统布局，同时成本也将增加。故无需额外装置而仅分析电流信号的诊断方法应用前景最广[6]。这涉及两方面内容：1）故障特征提取；2）故障自动诊断。基于电流分析的IM定子故障特征提取，目前有频谱分析法[7]、Hilbert变换[8]、经验模态分解[9]、谐波平面检测法[10]和对称分量分析法[11]等。关于故障自动诊断任务，目前最新的研究集中在人工智能技术方面[12-13]。但人工智能为黑箱数据处理结构，计算负担高，难以在工程实际中应用。

因此，本文引入统计学中广义似然比检验（generalized likelihood ratio test，GLRT）到IM定子故障检测中，设计了一种新型的故障诊断方法。文献[11]中的研究表明，在三相平衡电压下，负序和零序电流的相角和幅值可被视为稳定状态下IM定子故障的可靠指征。此外，对于闭环控制IM驱动系统，电机电流会受到控制回路的影响，这可能会影响到故障诊断。实际上，电流，转速和磁通闭环控制带宽均可能会对故障信号产生影响。对此引入GLRT算法，可突出受故障影响的IM电流对称分量，并能够可靠指示定子故障，实现准确的故障诊断。其中对三相电流采用最大似然估计（maximum likelihood estimation，MLE）来估计三相相量，并将GLRT算法用于不平衡故障检测。与基于FFT的诊断分析不同，MLE不依赖于频谱分析，而是使用时间信号模型来估计，从而增强了故障检测性能。

1 对称分量估计

对于由三相逆变器驱动的IM而言，每相定子电压都是经由PWM调制生成，由于开关频率较高，故可认为流经定子绕组的电流为正弦波，可表示为

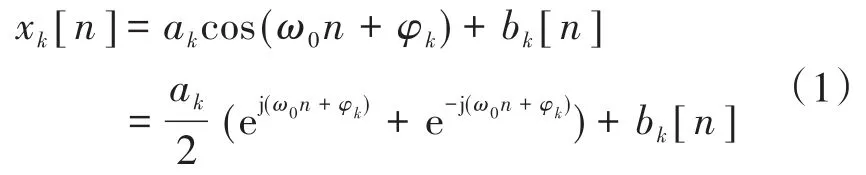
式中：ω0为基角频率；ak，φk分别为第k相电流（k=0，1，2）的幅度和初始相位；bk[n]（n=0，1，…，N-1）为额外噪声，N为总采样个数。

通常，在含有N个采样点的时间窗内对三相电流进行观察，故式（1）给出的信号模型可用矩阵形式表示如下：

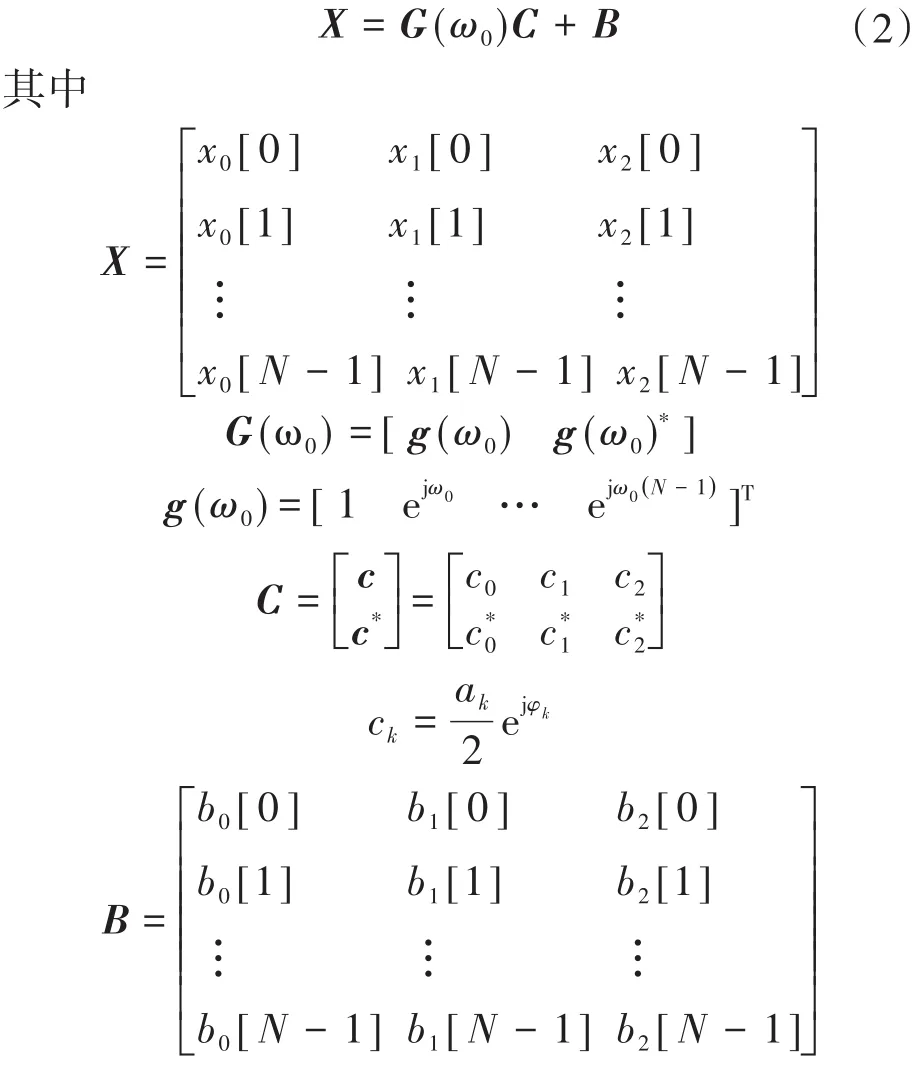
式中：“*”代表复共轭；ck为第k相上的固定相分量；B为噪声分量。

图1为三相IM在三相电流平衡和不平衡下的相量图。在三相平衡条件下，固定相量为ck=c0e-2jkπ/3，在不平衡条件下，幅值或相移将发生改变。

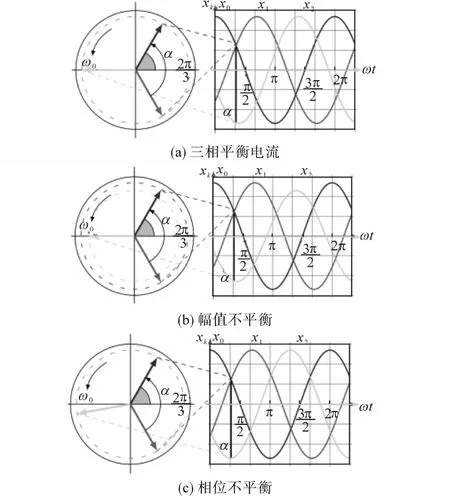
图1 定子正常和故障条件下的相量图Fig.1 Phasor diagram under healthy and faulty stator conditions

为了估计ω0和ck，可改写式（2）中信号模型，令x为一个3N×1的向量，其由矩阵X的列向量构成，如下式所示：

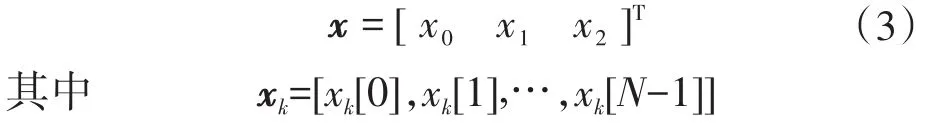
式中：xk为第k相电流。

因此，式（2）中的信号模型可描述如下：

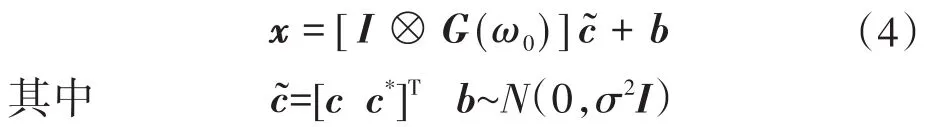
式中：“⊗”为克罗内克积；I为3N×3N单位矩阵；b为附加噪声，为具有零均值和方差为σ2的白高斯噪声。

本文所提出的方法分为以下两个实施阶段：1）基于三相定子电流测量，使用MLE估计ω0和ck；2）基于GLRT区分故障工况和正常工况。

对于式（2）中信号模型，ω0的MLE由下式给出：

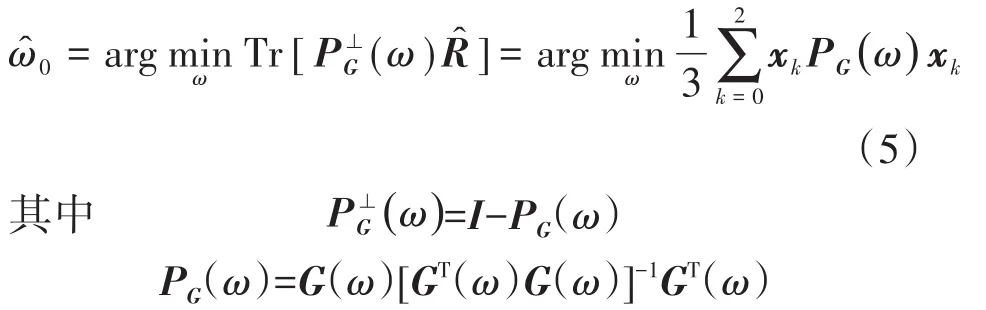
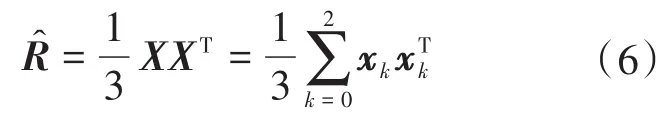
值得注意的是，上述最小化问题求解难度较小，因为其属于一维空间，后续采用单纯形搜索法处理即可。C的MLE由下式给出：

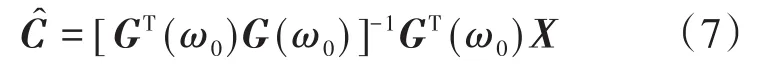
其中，ω0未知时，可由式（5）中的最大似然估计值代替。相量估计完成后可计算出正负序和零序分量。对称分量可使用Fortescue变换来计算如下：

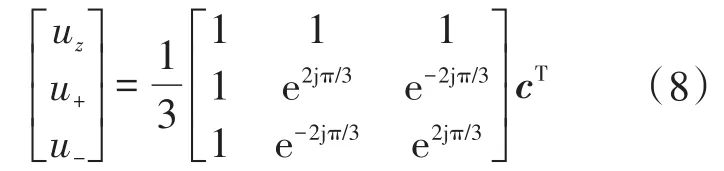
式中：uz，u+和u-分别为三相相量c的正、负序和零序分量。

c可用式（7）中的估计值代替。进一步可通过对相角，以及负序和零序电流进行分析，从而判定定子故障。

2 基于GLRT的定子故障诊断

定子故障检测可描述为两个假设检验问题如下：

1）H0：三相电流平衡，即ck=c0e-2jkπ/3。

2）H1：由于定子故障，三相电流不平衡。

由于假设H0和H1的概率密度函数具有未知参数，故两者为复合假设。在这种情况下，最佳检测通常是未知的。因此，考虑采用GLRT算法，其未知参数由其MLE估计值取代。

假设检验将基于对称分量进行。由于在三相IM驱动系统中通常使用三相三线制，零序分量始终为零，故对负序电流执行假设检验即可。

2.1 假设检验

IM正常运行（H0）或出现定子故障（H1）。H0和H1可重写为如下数学形式：

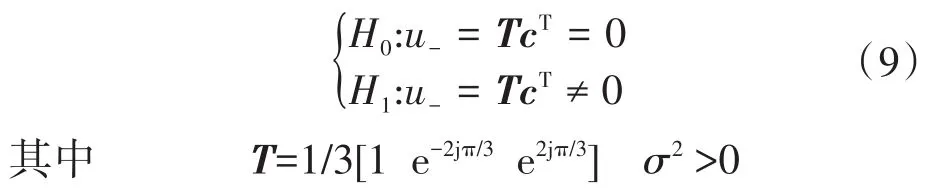
c的实部和虚部可表示如下：

基于上述描述，进一步可改写H0和H1为

上述假设检验问题可以通过将GLRT算法直接应用于式（4）中的信号模型进行求解。

2.2 广义似然比检验

在二元假设检验中，检测器的目标是确定两个假设中的哪一个最能描述信号X。Neyman-Pearson基本引理指出，在两个假设之间进行选择时，在给定的虚警率下最大化检测率的检测是似然比检验[14]。具体而言，对于不平衡故障检测问题，似然比检验确定H1是基于考虑是否满足下式：

当上述实际参数未知时，通常使用两种方法：Bayesian方法和GLRT方法。在Bayesian方法中，未知参数被视为随机变量。通过为每个随机变量分配先验概率密度函数，可以评估H0和H1的似然函数。但存在实践中难以选择先验概率密度函数的缺点。而通过将这些参数视为未知的确定性参数，则可获得替代方案，即GLRT算法。在GLRT算法中，可通过使用参数的MLE估计值来替换未知的确定性参数来评估似然比检验。GLRT算法中，对应似然比检验确定H1是基于考虑是否满足下式：

式中：γ为参数未知时检测阈值；J（x）为故障判据。

涉及ω0和的值，可考虑以下两种不同的情况：1）先验GLRT检测器，假定所有参数都是已知的；2）盲GLRT检测器，参数ω0和用MLE估计值替代。

检测器的性能指标为：1）检测率PD（即H1为真时检测为H1的概率）；2）虚警率PFA（即H0为真时检测为H1的概率）。这些判据是检测阈值γ的函数，由下式给出：

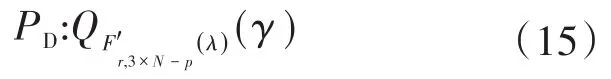
式中：Qf（x）为f个随机变量x的互补累积分布函数；Fr,3×N-p为分子自由度为r和分母自由度为3×N-p的F分布；F'r,3×N-p（λ）为分子自由度为r和分母自由度为3×N-p的非中心F分布，其中λ为非中心性参数，由下式给出：

由于PFA仅依赖于N，而与σ2和C无关，故虚警率恒定。此外，PD依赖于N和信噪比。

3 仿真分析

下面对GLRT故障诊断方案进行仿真分析，IM参数如下所示：额定功率Pn=1.5 kW，额定线电压Un=380 V，额定定子电流In=4.4 A，额定转速ωn=1 420 r/min，定子槽数Ns=48，极对数p=2，转动惯量J=0.042 6 kg·m2，额定频率fn=50 Hz，额定转矩Tn=10 N·m，定子电阻Rs=1.75 Ω，转子电阻Rr=1.68 Ω，定子电感Ls=295 mH，转子电感Lr=104 mH，互感Msr=165 mH。

图2为IM磁场定向闭环控制系统框图，采样频率fs设为10 kHz。首先IM在额定转速和转矩下运行，然后将附加电阻Rd（Rd=50%Rs）与定子一相绕组串联来模拟定子故障时的三相不平衡。图3为定子故障时三相不平衡电流仿真波形。电机绕组固有的低通滤波特性实际上会滤除谐波电压，而不会衰减基频分量的大小，从而相电流波形正弦度好，其低频分量对应式（1）中的信号模型。由图1可知，任何相电阻增加都会导致流过相应相的电流减小，但三相不平衡不是非常显著，需执行故障诊断算法才能自动检测故障并停机。

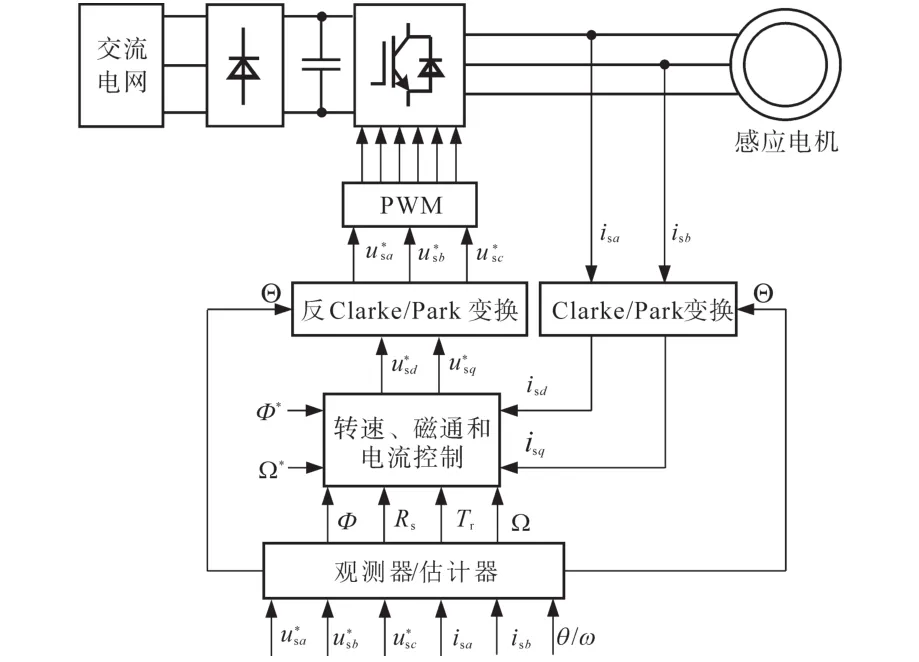
图2 IM闭环控制系统Fig.2 Closed-loop control system of the IM

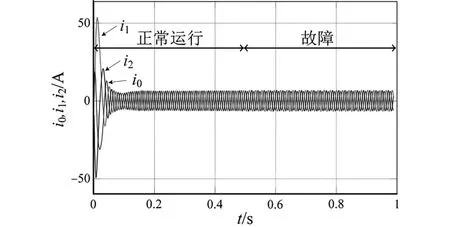
图3 定子故障时的三相不平衡电流仿真波形Fig.3 Simulation waves of three-phase unbalanced current with stator fault

进一步，对IM正常运行和故障状态下的定子电流进行数据采样，执行MLE以估计角频率ω0和相量ck。然后将定子检测问题转化为二元假设检验，并使用GLRT算法求解。测试中时间间隔Δt对应为1 000 个采样点，即1 s，而Rd从0 Ω开始，每间隔 Δt增加 25%Rs，直至Rd=Rs，对应模拟定子故障的发展。图4为GLRT算法输出故障判据J（x）的仿真结果，通过判断J（x）在定子电阻异常后跳变是否超过检测阈值γ，可迅速地辨识出定子故障。

图4 定子故障诊断仿真结果Fig.4 Simulation results of stator fault diagnosis

4 实验验证

在图5所示IM测试平台上进行了GLRT故障诊断方案的实验验证。其中测试IM参数与第3节仿真参数相同，由开关频率为10 kHz的三相逆变器驱动，负载由恒定励磁直流发电机带电阻器实现。定子故障通过在定子一相绕组上串联一个附加电阻Rd来模拟。IM磁场定向控制器由dSPACE系统（DS1104）实现。IM的定子电流通过使用LEM电流传感器进行测量，数据采集由一个采样率为20 kHz的16位AD转换器完成。

图5 IM测试平台Fig.5 Testing platform for IM

图6为投入Rd=25%Rs前后的正常和故障情况下的定子电流有效值波形。

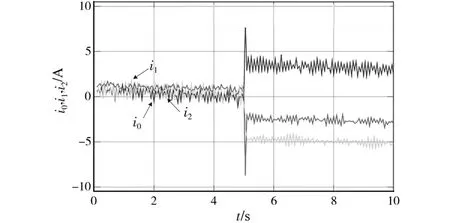
图6 定子故障时的三相不平衡电流实验波形Fig.6 Experimental waves of three-phase unbalanced current with stator fault

由图6可知，当发生定子故障时，三相电流的均方根值都会改变。因此，该参数可用作故障检测指示，但是无法辨识具体的故障相。此外，为了执行自动检测，必须将均方根值与分类技术或模式识别技术结合起来进行故障诊断，复杂度较高。

4.1 定子故障诊断

首先，控制IM以其额定速度运行，然后投入附加电阻Rd模拟定子故障，并将原始定子电流信号进行低通滤波处理并以1 kHz采样后施加GLRT诊断算法。图7为定子故障诊断实验结果。

图7 定子故障诊断实验结果Fig.7 Experimental results of stator fault diagnosis

图7a为IM正常运行和故障情况下的GLRT算法输出故障判据J（x）的直方图，图中His为频次。由图7a可知，两种工况下的直方图是不同的。因此，通过设置适当的检测阈值，可以以高置信度诊断定子故障。检测阈值γ是基于所需的虚警率PFA计算的，对于PFA=10-3，γ对应为24.43 dB，如图7b所示，J（x）超过阈值γ时则诊断为定子故障。此实验结果清楚地表明了所提出GLRT故障诊断算法的检测能力，即当只有很小程度的不平衡时即可快速检出。此外，还可以看出，对于正常运行工况，故障检测判据不等于零，其物理意义为：负序分量还代表了其他原因导致的不对称，例如逆变器输出电压误差导致的不平衡和传感器测量误差导致的不平衡等。

图8为GLRT算法输出故障判据J（x）在不同程度定子故障下的实验结果图，即Rd从0 Ω开始，以25%Rs为步长，逐渐增加至Rd=Rs来模拟不同程度故障。检测阈值γ仍为24.43 dB，对应PFA=10-3。图8中J（x）结果表明，对于正常运行IM，J（x）小于检测阈值γ，而当故障趋于严重时，J（x）的值将增大。这意味着新型诊断方案在正确检测故障的同时，还可以跟踪故障发展。

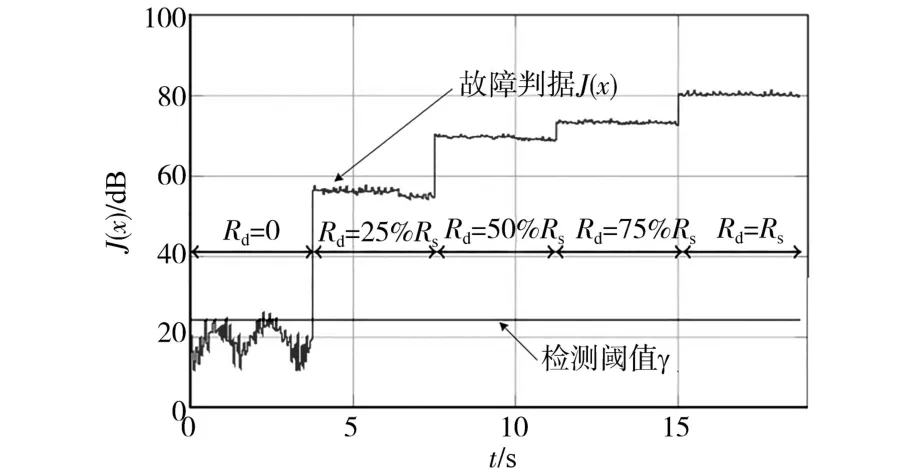
图8 不同程度定子故障诊断实验波形Fig.8 Experimental waves of stator fault diagnosis with different degrees

4.2 转速变化的影响

进一步，开展实验以评估所提出的定子故障诊断方案在不同转速下的故障检测能力。控制测试电机在额定转矩下运行，而定子电流频率分别设置为20 Hz，30 Hz，40 Hz和50 Hz进行测试。每次测试均对定子电流采样19 s，并对样本N=2 000的窗口宽度执行GLRT故障诊断算法。图9为不同转速和不同故障程度下的故障检测判据J（x）直方图。

由图9可以看出，定子电流频率为40 Hz和50 Hz时，直方图是不相交的，这意味着通过选择适当的阈值可以轻松实现故障诊断和故障程度判定。但当定子电流频率为20 Hz和30 Hz时，正常和故障状态下（Rd=25%Rs）的直方图存在一个重叠区，此时检测阈值γ可通过在5～20 s较大的时间窗口计算故障检测判据均值来设置，以实现有效定子故障诊断。

5 结论

本文设计了一种基于GLRT算法的IM定子故障诊断方案。在定子电压平衡时，负序和零序电流的相角和幅值可以视为稳态工作条件下判断IM定子故障的可靠指征。因此，采用MLE对角频率和三相相量进行估计，然后使用GLRT算法对定子电流不平衡性进行检测和诊断，从而快速诊断定子故障以及严重程度。仿真和实验结果验证了所提出IM定子故障检测方法具有低敏感性和高置信区间的优点，同时实施简便，且计算负担小。