激励频率影响下的松动故障转子非线性分析
刘桂珍,袁聪聪,陈正道,于 影,闻邦椿
(1.佳木斯大学机械工程学院,黑龙江佳木斯154007;2.东北大学机械工程与自动化学院,辽宁沈阳110819)
支座松动故障是旋转机械中危害较大的一种常见故障。松动故障会导致旋转机械产生周期性的被抬起、系统刚度发生变化并伴随周期性的碰摩。当松动量超过一定限度时,旋转机械将会产生运行故障甚至造成灾难性的事故。可见,转子系统的支座松动直接关系到转子的动态平衡与运行稳定性。因此,分析支座松动故障对转子系统的安全运行具有重要意义。
目前对松动故障的研究,都是基于分段线性力学模型基础上进行的。闻邦椿等[1]采用谐波平衡法分析得到了支承间隙系统的等效刚度;Goldman等[2]对具有支座松动故障转子的同频、倍频及分频振动进行了分析研究;Ji 等[3]用多尺度法分析了带有支座松动的转子-轴承自治系统的振动特性,揭示了稳态响应中如何判断分岔点的出现问题;Lee等[4-5]用传递矩阵法和谐波平衡法分析了支撑在线性和非线性轴承上的转子系统;段吉安等[6]考虑当发生松动故障时系统受到的周期性冲击作用,建立了松动故障的非线性力学模型,并分析了冲击作用对系统的影响;褚福磊等[7-8]应用现代非线性动力学理论,分析了带有一端支座松动故障的简单转子-轴承系统的复杂运动现象,讨论了转速变化时系统的多种形式的周期、拟周期和混沌运动,指出这类系统的某些周期运动的映射点结构具有慢变的特性;廖明夫等[9]利用进动分析方法,通过比较进动比函数在较大的转速范围内的明显变化,对支座松动故障进行了诊断研究,并通过实验验证了这种分析方法的有效性;文献[10-11]针对不同的对象,从不同的角度对基础松动问题进行了有效的诊断分析。
本文以转子系统具有支座松动故障为研究背景,利用拉格朗日方程建立了非稳态油膜力作用下的转子-定子-轴承系统松动故障的6 质量、12 自由度的非线性动力学模型,应用数值分析研究了当激励频率作为唯一控制参数时转子系统的响应,所得结论为该类转子的故障诊断和系统的安全运行提供理论依据。
1 力学模型与微分方程
1.1 拉格朗日方程描述
设有n个质点组成的质点系,受完整的理想约束,具有N个自由度,其位置可由N个广义坐标方程来确定。则有
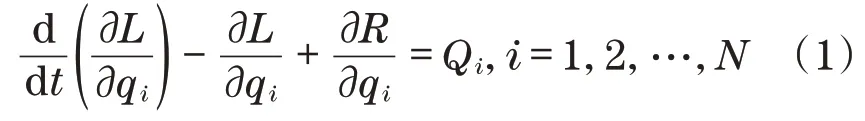
式中:L为拉格朗日函数,L=T-V,其中T为系统的动能函数,V为系统的势能函数;R为与系统阻尼相对应的耗散函数;Qi为作用在系统上的广义力;qi为系统独立的广义坐标;N为系统的总自由度个数。
1.2 非稳态油膜力模型[12]
非线性油膜力模型采用短轴承假设下的Capone 非线性油膜力模型,该模型有较好的精度和收敛性。在短轴承油膜力假设条件下的无量纲雷诺方程为

式中:h为无量纲油膜厚度为油膜厚度,C为轴承径向间隙);z为无量纲轴向位移,z=为轴向位移);p为无量纲油膜压力,p=为油膜压力,μ为油膜黏性系数);x、y分别为无量纲轴颈中心x、y方向的位移分别为无量纲轴颈中心x、y方向上的速度分量。
由式(2)可得无量纲油膜压力为
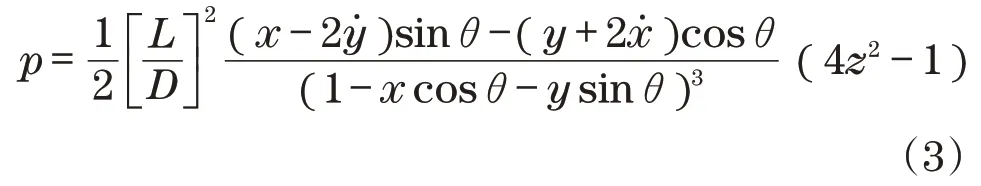
式中:D为轴承直径。
无量纲非线性油膜力最终可以表示为

1.3 力学模型
带有两端支座松动故障的转子-定子-轴承系统如图1 所示。假定系统中两端支座同时出现松动,轴颈两端由相同的油膜轴承支撑,设δ为轴颈与轴承间的平均间隙,O1为转盘的几何中心,Oc为转盘的质心,m1为转盘处的等效集中质量,O2、O3分别为两端轴颈的几何中心,O4、O5分别为两端轴承的几何中心。两端轴承支座质量相等,即m2=m6,两端轴颈在轴承处的等效集中质量相等,即m4=m5,定子支座质量为m3。
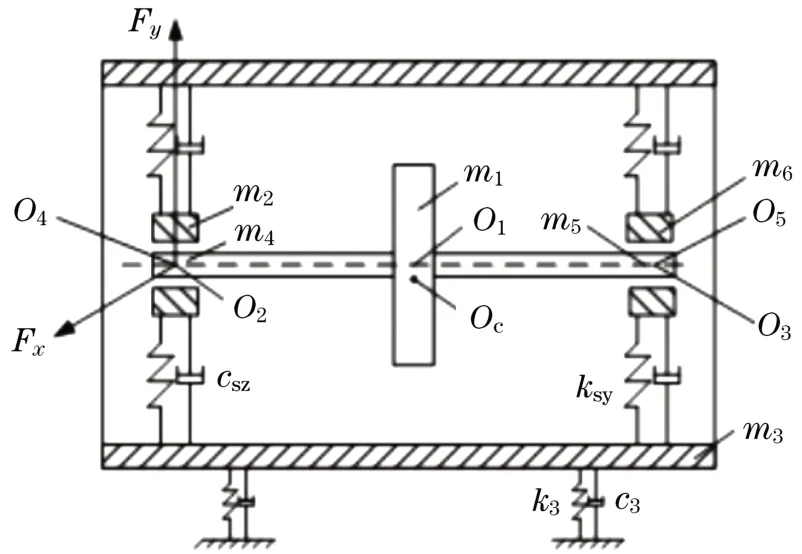
图1 转子-定子-轴承系统松动故障的动力学模型Fig.1 The dynamics model of rotor-stator-bearing system with looseness fault
假设圆盘与轴颈之间为无质量弹性轴,k1为转轴刚度系数,k2为轴承支撑刚度系数,k3为定子基础刚度系数,kr为轴承座与基础之间的等效刚度,ksz、ksy分别为松动端左、右轴承座的分段刚度,单位为N•m-1;c1为转轴阻尼系数,c2为轴承支撑处的结构阻尼系数,c3为基础对定子的阻尼系数,csz、csy分别为松动端左、右轴承座的分段阻尼,单位为N·s·m-1。
1.4 运动微分方程
设盘心O1和轴颈中心O2、O3的位移分别为(x1,y1)、(x2,y2)、(x6,y6),ω为轴的转动角速度,e为不平衡量,μ为油黏度,R为轴颈半径,L为轴颈长,Fxz、Fyz和Fxy、Fyy分别为左、右两端轴承受到的油膜力。
根据拉格朗日方程,对图1 建立具有两端松动故障的转子-定子-轴承系统的质点运动微分方程组:

当松动发生时,设松动的最大无量纲间隙值为δ1,分段线性表示为
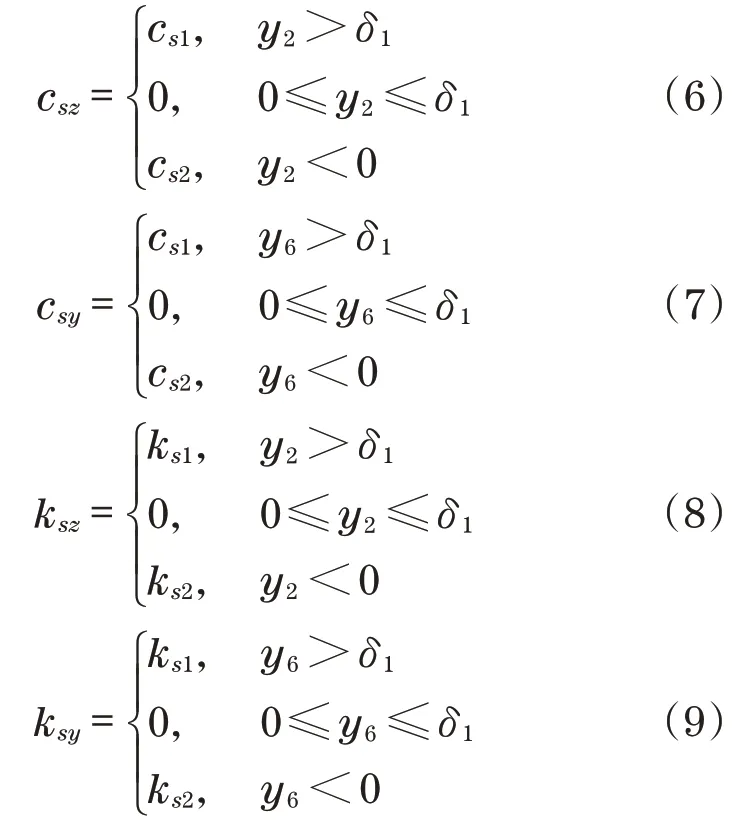
2 数值模拟
运用4 阶Runge-Kutta 法对数值进行求解,在计算中为了能够较快地得到稳定解,应将步长选得尽量小且周期足够多。
为了保证解的收敛性并减小计算误差,计算中需要选用较小的时间步长,同时为了能记录到振动的稳定解和消除瞬态响应的影响,略去前2 000个数据点,取后4 500个数据点。计算轨迹图时取10~20个周期。设系统的参数为m1=4.0 kg,m2=m6=32.1 kg,m3=50.0 kg,m4=m5=20.0 kg;R=25 mm,δ2=0.2 mm,b=0.1 mm,e=0.1 mm,μ=0.018 Pa·s,c1=1 050 N·s/m,c2=2 100 N·s/m,c3=2 100 N·s/m;k1=2.5×105N/m,k2=2.5×105N/m,k3=2.5×107N/m,ks1z=1.0×106N/m,ks2z=20.0×106N/m,ks1y=5.0×106N/m,ks2y=10.0×106N/m;cs1z=1 500 N·s/m,cs2z=1 500 N·s/m,cs1y=1 500 N·s/m,cs2y=1 500 N·s/m,c43=350 N·s/m,δ1z=0.01 mm,δ1y=0.01 mm,轴承有效长度L=12 mm。
非稳态油膜力作用下的松动故障转子系统以激励频率作为唯一控制参数时的分岔图如图2所示,可以发现,随着激励频率的变化,转子系统存在周期1、拟周期、周期4和混沌等多种非线性运动形式。
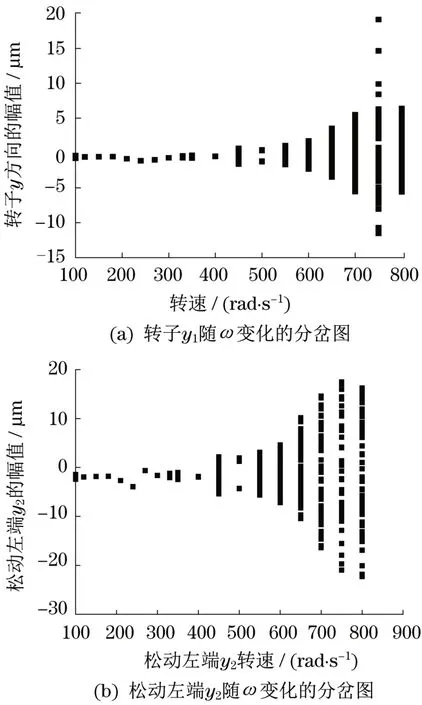
图2 激励频率ω变化时y1和y2的分岔图Fig.2 The bifurcation diagrams with ω changing of y1 and y2
由于分岔图无法辨别出拟周期运动和混沌运动,结合分岔图所对应不同激励频率下的庞加莱映射图作进一步深入研究,得出系统的运动轨迹如下:
当转动角速度ω=90 rad/s 时,Poincare 映射点为一个封闭的曲线,表明此时转子系统处于拟周期运动;当转动角速度ω=100 rad/s 时,Poincare 映射点为分布在一定区域上的不可数点集,表明此时转子系统处于混沌运动;当转动角速度ω=120 rad/s时,转子系统处于拟周期运动;当转动角速度ω在(150,210)rad/s时,Poincare映射点为1个孤立点,表明此时转子系统处于P-1运动;当ω=240 rad/s时,转子系统处于拟周期运动;当转动角速度ω在(270,300)rad/s 时,转子系统处于P-1 运动;当ω在(330,450)rad/s时,转子系统处于拟周期运动;当转动角速度ω=500 rad/s时,Poincare映射点为4个孤立点,表示此时转子系统处于P-4运动;当转动角速度ω在(550,1 000)rad/s 时,转子系统处于混沌运动。
在其他参数保持不变、把激励频率作为唯一控制参数时,结合图2 所示的分岔图和不同激励频率下的转子系统的Poincare 截面图,可以发现随着激励频率的变化,转子系统存在周期1、周期4、拟周期和混沌等多种非线性运动。研究结果表明,当转动角速度ω在(90,1 000)rad/s 区间变化时,系统经历了“拟周期运动→混沌运动→拟周期运动→P-1 运动→拟周期运动→P-1 运动→拟周期运动→P-4运动→混沌运动”的复杂过程。
3 结论
通过对松动故障转子系统随激励频率变化的研究,得出以下结论:
(1)在非稳态油膜力作用下,转子-定子-轴承系统出现松动故障时,松动故障转子系统表现出对激励频率变化具有极高的敏感性,系统在频率小幅变化下呈现周期1、拟周期、周期4、混沌等多种复杂运动,最后经过周期4分岔进入混沌运动状态。
(2)当支座发生松动时,支座的相轨迹呈现出特殊的形状,这为有效识别转子-轴承系统的支座松动故障提供了理论依据。

