基于2自由度μ综合控制器的液压挖掘机运动控制研究
李云峰,魏培鲜
(1.山西交通职业技术学院工程机械系,山西太原030600;2.黄河交通学院汽车工程学院,河南武陟454950)
液压挖掘机是一种在基建、工业、建筑等领域中被广泛应用的工程机械。随着液压挖掘机被应用到越来越多的行业中,其工作的环境也愈发多样化。通常情况下,挖掘机的工作环境恶劣,存在大量的噪声和烟尘的污染,给挖掘机的控制过程带来巨大的干扰,增加了挖掘机的操控难度[1]。因此,面对复杂工作环境带来的巨大扰动,提高挖掘机在复杂工况下控制的精度和稳定性尤为重要[2]。
相关学者对液压挖掘机的回转控制做了大量的研究[3-5],但是,由于液压挖掘机固有的非线性结构特性在其控制上产生巨大扰动,给控制带来了巨大的挑战。因此,对液压挖掘机的控制问题,大多数研究者都采用非线性控制技术来处理特定非线性有关的不确定性[6-7]。例如,文献[8]为了提高挖掘机的控制精度,建立了挖掘机电液控制系统的非线性模型,设计了带有死区补偿的分段控制器,实验结果验证了带有死区补偿的分段控制器可以较好地克服挖掘机的非线性特性。文献[9-10]采用了粒子群优化算法(Particle Swarm Optimization,PSO)对液压挖掘机的PID 增益等控制参数或模糊控制器参数进行优化,以提高传统控制器的性能。文献[11]针对液压伺服系统逆模型的学习问题,提出了一种基于反馈神经网络的在线学习控制方法,其优点是不需要一个确定的液压伺服控制系统模型,就能实现对系统的精确控制。文献[12]通过分析试验机负载独立流量分配系统的工作原理建立了数学模型,并根据数学模型与试验完成了自适应控制器的设计,结果表明,自适应控制的效果和响应速度有了一定的提高。虽然,上述控制方法考虑了系统的不确定性和外部干扰,但无法保证在整个挖掘机工作区域内的鲁棒性能。
对此,本文针对未知的非线性挖掘机回转控制结构进行分析,建立了挖掘机回转系统和液压伺服系统模型。考虑到挖掘机是一个复杂的液压系统,有各种非线性因素的影响,采用视为参数不确定线性系统的内环闭环动力学作为外环控制系统,设计了2 自由度µ综合控制的液压挖掘机鲁棒控制系统,实现对液压挖掘机的鲁棒性控制。最后,对本文设计的控制器进行了阶跃信号、干扰信号和回转路径轨迹跟踪实验。
1 回转驱动结构
对挖掘机液压回转系统驱动结构进行构建,如图1所示。
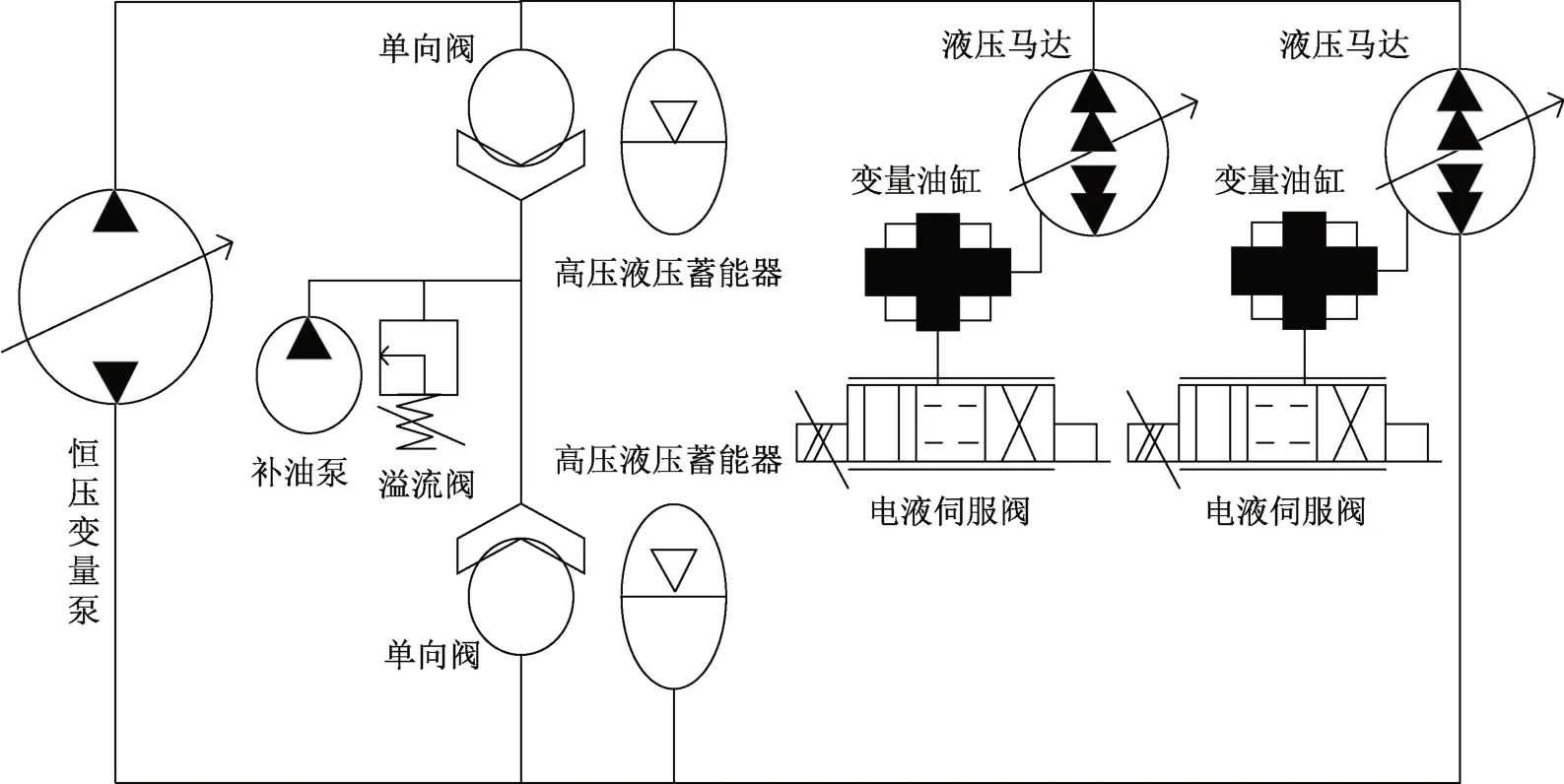
图1 回转系统原理图Fig.1 Schematic diagram of rotary system
回转系统包括恒压变量泵、辅助动力源高压液压蓄能器、补油泵、溢流阀、单向阀、液压马达、变量油缸和电液伺服阀。其中,液压马达、变量油缸和电液伺服阀共同组成回转系统执行系统,连接回转机构,通过控制液压泵的流量输出,从而控制液压挖掘机回转过程。恒压变量泵是整个系统的动力核心,为回转过程提供动力。同时,为提高回转系统在速度突变情况下的控制精度,对回转系统动力进行补偿,提供了高压液压蓄能器,有效地辅助回转系统的加速运动,提高其控制精度。
2 回转系统建模
根据图1所示的回转控制驱动系统,对回转执行机构进行建模,液压泵和伺服阀主要完成对回转机构的控制,因此,根据液压泵流量特性,其模型如下:
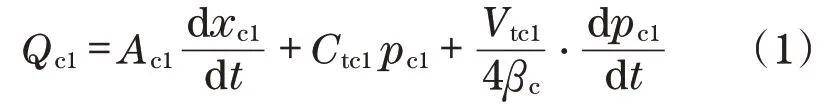
式中:Vtc1为液压缸总容积;xc1为油缸活塞位移;pc1为油缸压力;Ctc1为油缸泄漏系数;Ac1为油缸作用面积。
根据油缸作用力平衡条件得
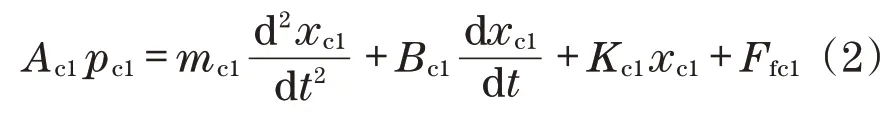
式中:Bc1为油缸黏性阻尼系数;Kc1为油缸弹簧等效刚度;mc1为油缸等效活塞质量。
油缸作用力与油缸作用力面积、油缸压力有关,另外还受到活塞和回转之间的作用力Ffc1的影响。因此,液压马达排量D1与最大排量D1max的比值等于回转角度αc1和回转最大回转角度αc1,max的比值,即

电液伺服阀控制模型可以表示为[13]
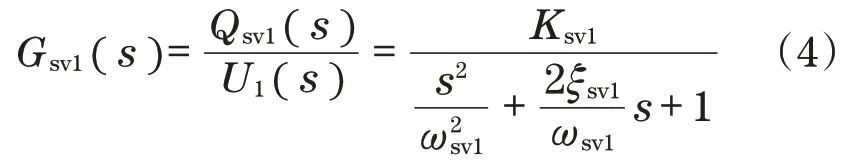
式中:Ksv1为电液伺服阀流量增益;ξsv1为伺服阀阻尼比;Qsv1为电液伺服阀输出流量;ωsv1为固有频率;U1为输入电压。
假设电液伺服阀频率远高于液压控制系统,则式(4)可以简化为
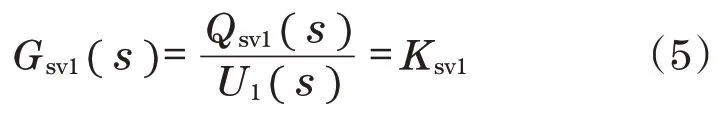
根据电液伺服阀输出流量,稳态工作点附近变量油缸流量Qp/mc1可以表示为
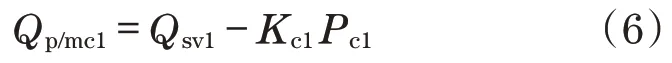
根据液压马达运动平衡方程,回转平台动力学平衡方程可以表示为
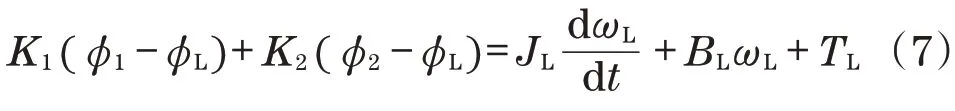
式中:JL为等效转动惯量;BL为等效黏性阻尼系数;φ1和φL为液压马达转角和输出端转角;ωL为转速;TL为转动惯量。
对式(7)进行拉普拉斯变化:
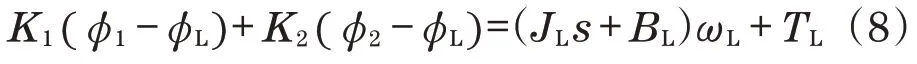
根据式(3)和式(8),通过对挖掘机回转角度的精确控制,可以提高挖掘机运动的控制精度。
3 控制系统设计
3.1 控制系统
控制系统采用内环控制结合外环反馈控制。为便于模型识别,使内环系统响应线性化,利用PD控制和死区补偿共同构成内环控制系统。引入µ综合控制法设计鲁棒控制器作为系统模式不确定参数的补充,控制结构框图如图2所示。

图2 控制框图Fig.2 Control block diagram

由于在滑阀打开流入气缸的流量后,气缸内压力积聚需要时间,造成系统内部延迟,因此,采用PD 控制器忽略了积分项,避免由于死区时间内误差的积累。
根据图2,内环控制系统状态参数有不确定性,将内环控制系统的闭环动力学作为目标对象,采用2 阶系统µ综合控制设计鲁棒控制器,内环控制可以表示为
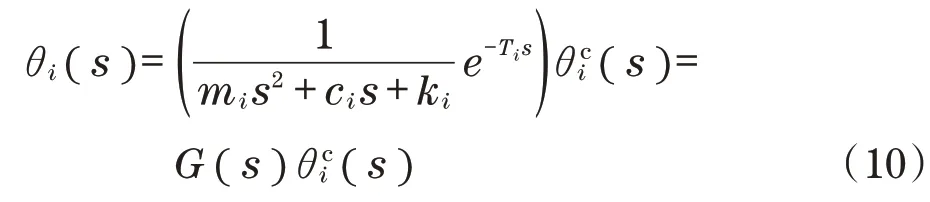
式中:m、c、k为内环系统建模参数;T为时间延迟。
假设正参数mi、ci、ki、Ti相对于标称值具有一定的不确定性。设定参数值和范围,根据系统的时间响应,确定2 阶系统的参数,并且根据输入变化和输出变化之间的时差估计时间延迟。
3.2 μ综合鲁棒控制器设计
外环反馈控制采用2自由度µ综合鲁棒控制器设计,其结构如图3所示。
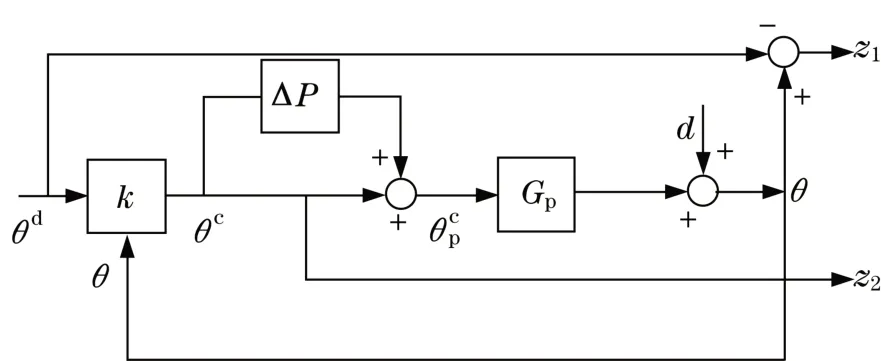
图3 2自由度控制结构Fig.3 Two degrees of freedom control structure
图中:θd、d 为命令输入信号和外部扰动信号;z1、z2为跟踪性能和输入用法的输出为控制输入和扰动控制输入。
由于不确定性系统扰动结构化特性,控制器k通过反馈控制和滤波器使得系统的结构奇异值满足以下条件:
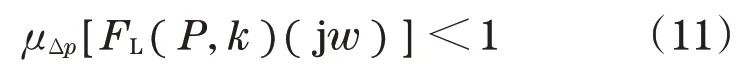
式中:Δp为不确定结构块;FL(P,k)为P和k的下分数变换;控制器k采用D-k迭代法进行理论设计。
此外,鲁棒控制对象的动力学模型可表示为
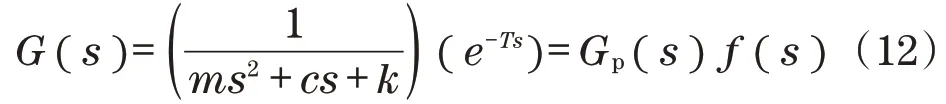
式中:f(s)=e-Ts;Gp(s)为参数变化函数,可定义为
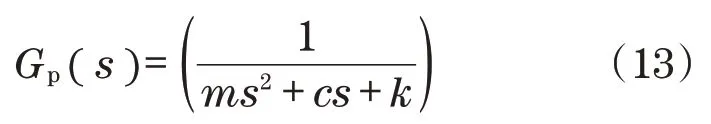
考虑到未建模动态,将不确定性结构作为不确定项存在于执行器中,即
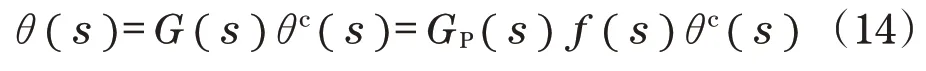
忽略动态信息引起的相对不确定度的大小可表示为
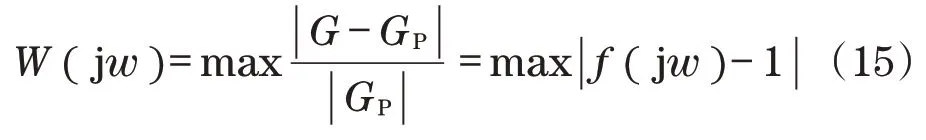
然后,通过确定频率响应的上限选择相对不确定度:
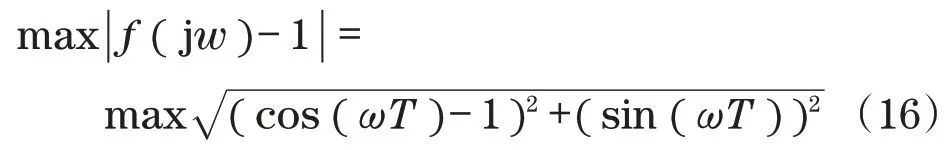
因此,内环控制系统的不确定度模型为
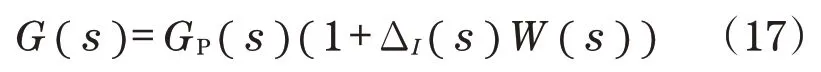
式中:|ΔI(s) |∞≤1 为对应于未建模动力学的复杂不确定性。
利用µ综合鲁棒控制器有效地对不确定系统结构的扰动进行补偿,提高回转角度控制精度。
4 实验结果
根据液压回转控制系统模型,对设计的µ综合鲁棒控制下的回转速度进行控制,在Matlab/Simulink 环境下,建立仿真模型,对阶跃输入信号、干扰信号和回转路径轨迹进行跟踪测试,液压马达的仿真实验参数如表1所示。
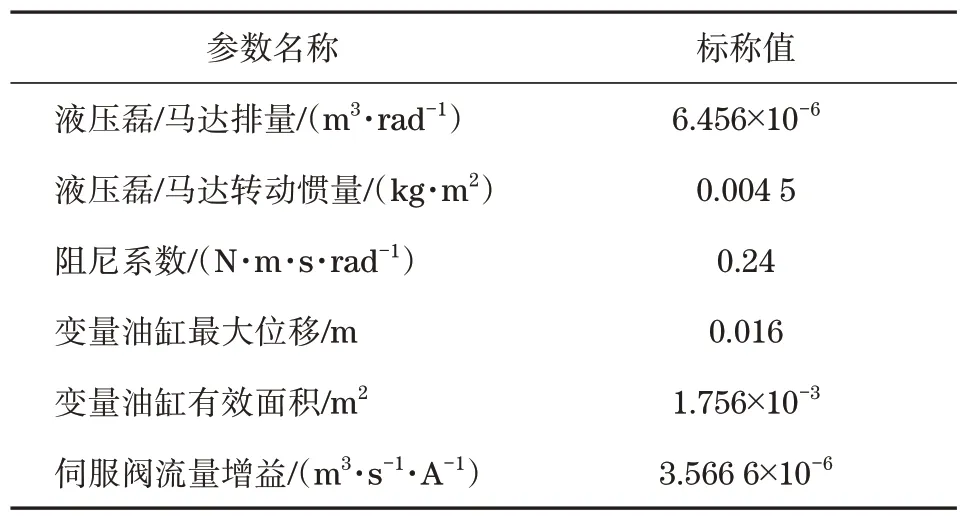
表1 液压磊/马达仿真实验参数Tab.1 Hydraulic control/motor simulation test parameters
4.1 阶跃信号响应
图4为阶跃信号下,PD 控制和µ综合鲁棒控制下挖掘机液压回转控制系统对回转角度的控制。从图中可以看出,回转速度在PD 控制和µ综合鲁棒控制下经过一定的校正,获得稳态的输出。其中,PD 控制下回转控制系统校正时间大概为14 s,而µ综合鲁棒控制的校正时间大约为6 s,缩短了57%。稳态输出时,µ综合鲁棒控制下的稳态误差明显小于PD 控制。说明相比于PD 控制,采用µ综合鲁棒控制不仅能够有效地减小过渡时间,而且能够降低超调量,提高控制精度。

图4 阶跃信号响应曲线Fig.4 Step signal response curve
4.2 扰动信号响应
设定速度为90 rad/s,在t=10 s 时,液压回转系统分别受到扰动信号50 N·m 和100 N·m 的干扰,其响应曲线分别如图5 和图6 所示。在扰动信号Q为50 N·m 时,2 种控制都能够及时对扰动进行反馈,并保持较好的跟踪效果。PD 控制下,回转速度的超调量达到85 rad/s,而µ综合鲁棒控制下的回转速度的超调量只有87 rad/s。同时,µ综合鲁棒控制下的稳态调整时间比PD控制下扰动稳态时间缩短了约10 s。随着干扰信号Q增加到100 N·m时,µ综合控制下的系统超调量有所增加,但是与PD 控制相比,超调降低了一半,稳定时间减少10 s。说明在负载扰动的情况下,µ综合鲁棒控制能够对扰动信号进行补偿,相比于PD 控制器具有良好的跟踪和控制性能,系统的鲁棒性得到了提高。

图5 扰动信号Q=50 N·m时的响应曲线Fig.5 Response curve of perturbation signal Q=50 N·m
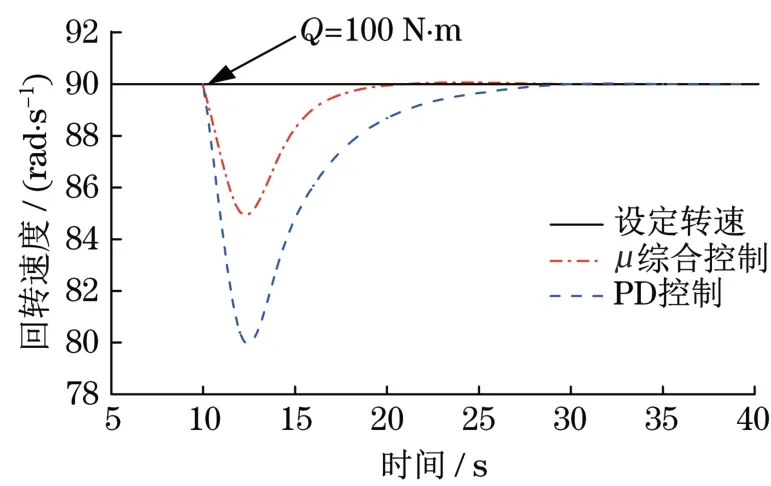
图6 扰动信号Q=100 N·m时的响应曲线Fig.6 Response curve of perturbation signa Q=100 N·m
4.3 运动轨迹跟踪
为了进一步验证本文所提控制系统的性能。考虑实际工作状况,在连续指令下,回转角度进行测试,不同控制器下回转角度的变化如图7 所示。在回转角度指令不断变化过程中,不同的控制器都实现了对指令的有效跟踪。在跟踪误差方面,µ综合鲁棒控制下的回转控制误差明显小于PD 控制。在回转路径发生较大变化时,PD 控制下的稳定性都不如µ综合鲁棒控制。说明µ综合鲁棒控制对系统的可变参数和不确定结构的影响有较好的补偿机制,能够有效地对运动指令进行跟踪控制,提高了液压回转控制系统的鲁棒性和稳定性,达到了预期的效果。而PD控制对未知的结构和参数扰动的响应缺乏补偿机制,相比于µ综合鲁棒控制,其控制效果较差。
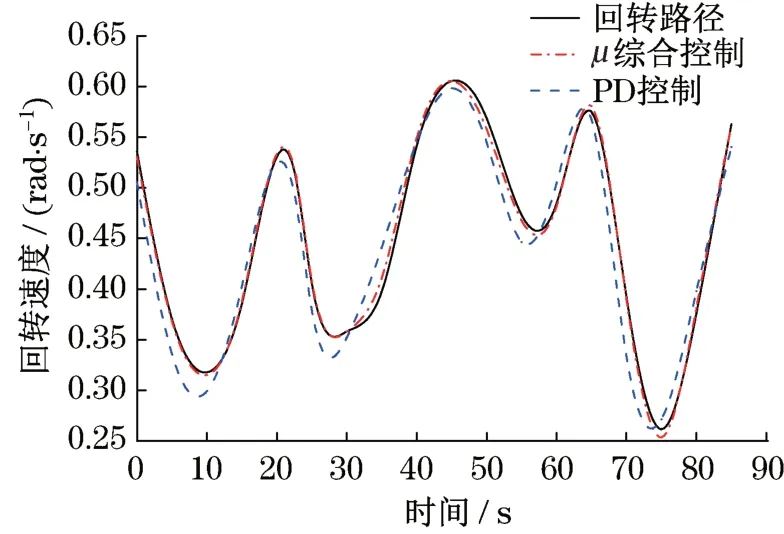
图7 回转角度跟踪曲线Fig.7 The rotation angle tracks the curve
6 结语
本文构建了挖掘机液压回转控制结构,建立了液压伺服控制系统模式,考虑到不确定性的扰动,利用PD 控制和死区补偿共同构成内环控制,在此基础上开发了2自由度µ综合控制来实现系统的鲁棒控制;并在Matlab/Simulink 环境下进行了阶跃信号、干扰信号和回转路径轨迹控制实验,与传统PD 控制方法进行了比较分析。结果表明:面对扰动信号,2 自由度µ综合控制器具有较快的响应速度和较高的控制精度,同时能够实现对回转运动轨迹的高精度跟踪,具有较好的鲁棒性和稳定性。

