不同加载路径条件下软弱夹层泥岩力学响应 及变形规律

张晓悟，徐金海，刘智兵，孙 垒

( 1. 中国矿业大学 矿业工程学院，江苏 徐州 221116；2. 煤炭资源与安全开采国家重点实验室(中国矿业大学)，江苏 徐州 221116 )

长期的成岩过程，使得地下岩体呈现层状结 构[1]。相比于岩石而言，岩体的结构较为复杂，其力学性能主要由岩体内较弱的岩层决定[2]。大量的研究表明，岩体空间内软弱夹层的存在会导致隧( 巷 )道和边坡结构更易破坏和失稳[3-7]。因此，对软弱夹层内岩石的力学响应及变形特征的研究是非常必要的。

诸多学者对地层结构中软弱夹层进行了大量研究。张泽林[8]等研究了不同倾角软弱夹层剪切力学特性和破坏特征，提出软弱夹层倾角在一定范围时，剪切破坏在软弱夹层内发生，超出该范围时，则破坏发生在软弱夹层外；陈鑫[9]等分析了室温和冻融状态下不同软弱夹层厚度比的水泥土力学特性，发现软弱夹层抗压强度、弹性模量和应变与厚度比表现出明显相关性；徐卫亚[10]等研究了含软弱夹层的层状岩体的流变特性，建立了反映含软弱夹层的层状岩体的力学性能流变模型；蒲成志[11]等利用岩石剪切试验机，对含薄层黏土充填结构面的岩石进行了研究，提出薄层黏土充填结构面只有少部分面积在抗剪过程中发挥作用，且随法向应力增加，该部分面积增加速率减小；宋彦琦[12]等研究了不同倾角软弱夹层下大理石力学特性和破坏形式，提出受载过程中软弱夹层处发生剪切滑移，发现当软弱夹层倾角为60°时，大理石弱化最明显；李剑光[13]通过对含倾斜软弱夹层复合岩体进行瞬时和蠕变试验，得出随着软弱夹层厚度的增加，复合岩体更易破坏，并建立了含倾斜软弱夹层复合岩体的蠕变模型；王宇[14]等研究了坝基岩体中软弱夹层剪切蠕变的特征，分析了软弱夹层的剪切蠕变规律、含软弱夹层坝基岩体的破坏机制及长期强度；姜德义[15]等对不同软弱夹层特征的盐岩进行试验研究，发现软弱夹层厚度和分布均对盐岩力学特性、变形特征和破坏形式有显著影响。

软弱夹层在地层中的分布与隧( 巷 )道相对位置的不同，将导致在隧( 巷 )道开挖时含软弱夹层的围岩结构在三向地应力状态下应力重新分布的不 同[16-17]，即：当软弱夹层位于隧( 巷 )道帮部时，其首先是水平应力的卸压；当软弱夹层位于隧( 巷 )道顶部时，其首先是垂直应力的卸压。因此，单纯通过传统力学试验而不考虑应力路径的变化，对软弱夹层所进行的研究与实际生产是脱离且不全面的。此外，现有的研究主要针对软弱夹层的倾角、厚度等因素对复杂岩体的力学特性、变形特征和破坏形式的影响，而针对软弱夹层本身的力学特性和变形特征的研究较少。因此，笔者通过对地下构造区域内的软弱夹层泥岩进行现场取样，并设计4种应力路径下的软弱夹层泥岩试件的三轴压缩试验，分析应力路径和围压对软弱夹层泥岩力学特性及变形规律的影响，提出了应力路径和围压作用下软弱夹层泥岩力学特性及变形规律表征参量，为含有软弱夹层的岩体稳定性分析和空间结构承载能力判断提供参考。

1 试 验

1.1 试件制备

山西宁武某矿地下400 m处于构造区域，巷道掘进期间揭露厚度1.4 m的软弱夹层泥岩，该层软弱夹层泥岩随巷道掘进由巷道底板逐渐向顶板发展，且其走向与巷道掘进方向基本一致，预计影响巷道长度为180 m。当软弱夹层泥岩位于巷道底板时，由于应力集中，其所受到的应力值最大，达到28 MPa；当软弱夹层泥岩位于巷道中部时，其所受到的应力值最小，约3 MPa。因此，本文在对软弱夹层泥岩进行试验设计时，按均匀间隔将初始径向围压设计为5，15，25 MPa，以贴合现场实际情况。根据已揭露情况，该软弱夹层泥岩力学性能较一般泥岩强度低、变形量大，表现出明显的黏塑性，不利于围岩稳定和巷道的支护。

为保证研究对象的匀质性和可对比性，对软弱夹层泥岩采用空心圆筒进行原位取样，并确保所取试样必须距离上下层理面40 mm以上，如图1所示，然后将取回试样用软岩制备机，按照国际岩石力学学会规范要求[18]，加工成尺寸为φ50 mm×100 mm的标准试件，如图2所示。

图1 现场取样示意 Fig. 1 Field specimen signal

图2 试样的制备 Fig. 2 Specimen preparation

1.2 试验仪器及步骤

采用伺服控制岩石三轴测试系统( MTS-4000 )对试件进行三轴压缩试验。试验过程中应变变化通过在试件表面安装的应变片进行收集、监测。

试验共设计4个应力路径，如图3所示。应力路径1为保持径向应力不变，增加轴向应力至试件破坏；应力路径2为增加轴向应力，减少径向应力；应力路径3为保持轴向应力不变，减少径向应力；应力路径4为同时减少轴向应力和径向应力。

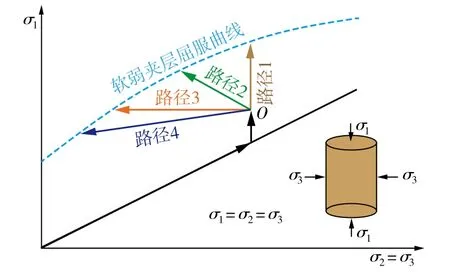
图3 不同应力路径示意 Fig. 3 Different stress paths

以应力路径2为例，试验设计的具体实现分为3个步骤：

步骤1：先将试块放入伺服机试验平台，并施加0.5 kN轴向应力以固定试块，然后采用应力加载控制，按照0.05 MPa/s对试件同时加载轴向和径向应力至设计值，并保持径向应力不变5 min。试验中共设计3种径向应力，分别为5，15，25 MPa。

步骤2：采用应变控制，按0.005 mm/s的速率将轴向应力逐步施加至极限抗压强度的70%。

步骤3：采用应力控制，按0.5 MPa/s的速率增加轴向应力，同时按0.25 MPa/s的速率降低径向应力( 轴向与径向应力的加载变化速率比为2∶1 )，直至试件达到最大变形量或发生破坏。

应力路径3和4的前2个步骤与应力路径2的相同，主要区别在步骤3，其中应力路径3为保持轴向应力不变，按0.25 MPa/s的速率减少径向应力，直至试件达到最大变形量或发生破坏；而应力路径4则按0.125 MPa/s的速率减少轴向应力，同时按0.25 MPa/s的速率降低径向应力( 轴向与径向应力的加载变化速率比为1∶2 )，直至试件达到最大变形量或发生破坏。

为减少试验误差，每组试验进行3次，并取平均值进行分析。试验分组情况见表1。

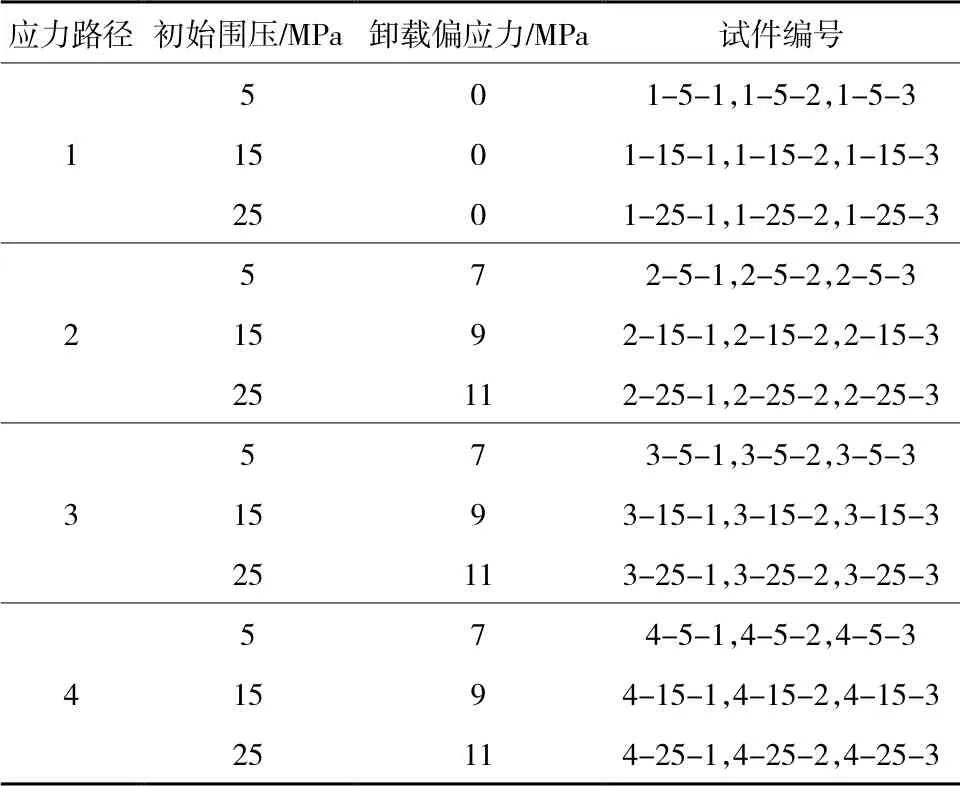
表1 试验分组情况 Table 1 Test grouping

2 试验结果分析

2.1 偏应力-应变曲线分析

图4为应力路径1条件下软弱夹层泥岩试件的偏应力( 轴向应力与侧向应力差值 )和应变之间的关 系曲线。

图4 应力路径1条件下试件偏应力-应变曲线 Fig. 4 Deviatoric stress-strain curves of specimen under stress path 1

由图4可知，不同围压条件下，试件的力学响应各不相同，即：围压越高，偏应力越大，试件能承受的强度越大；随着围压的增加，试件表现出塑性流动的特征，特别当围压达到15，25 MPa时，试件甚至出现应变强化现象；试件在三轴压缩条件下，体积先收缩后膨胀，当围压较小时，膨胀现象更加明显。

图5为应力路径2，3，4条件下偏应力与轴向、径向应变和体积应变的曲线。由于试验过程中前2个步骤相同，因此仅取步骤3( 即图3中O点以后 )过程中的应力-应变关系进行研究。

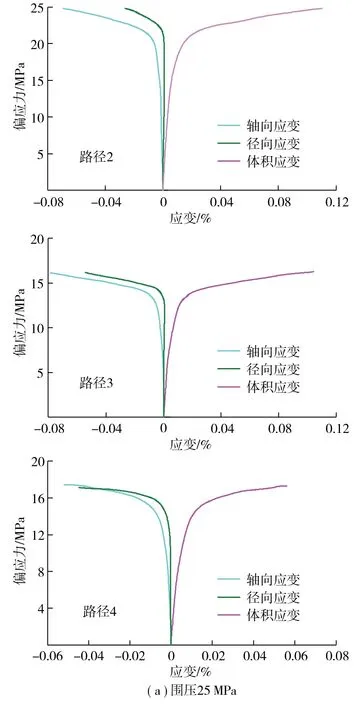
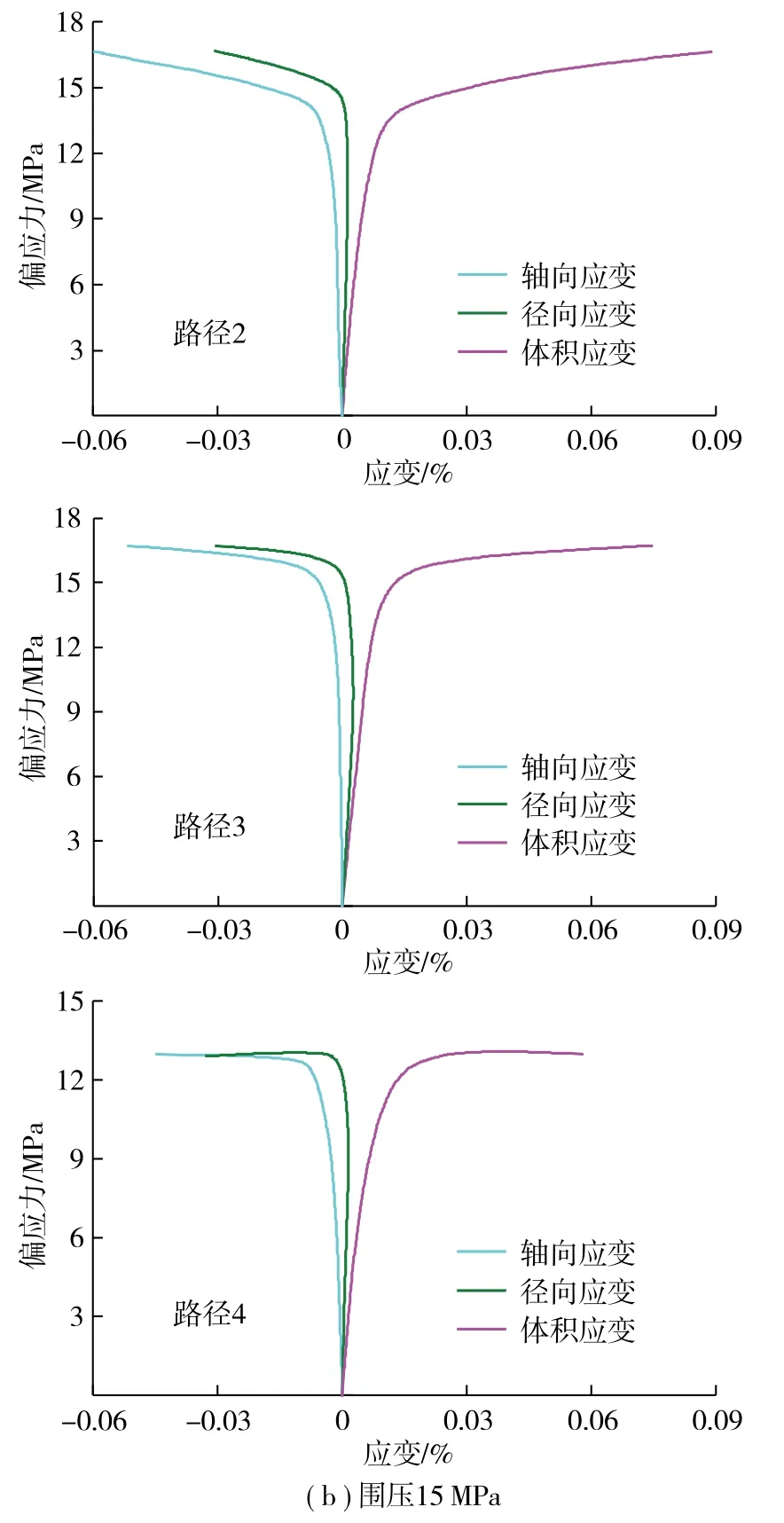
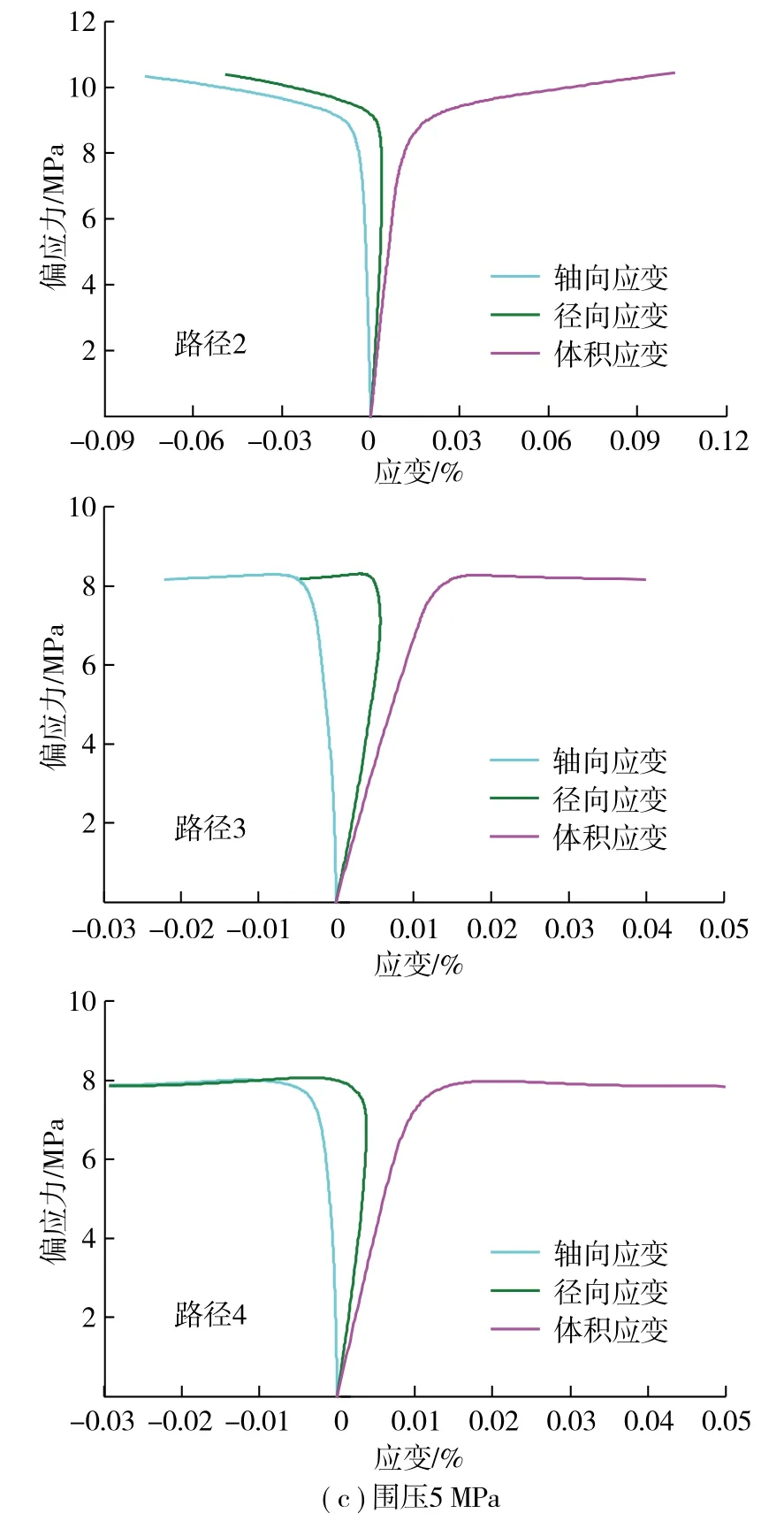
图5 应力路径2，3，4条件下试件应力-应变曲线 Fig. 5 Stress-strain curves of specimen under stress paths 2，3 and 4

由图5可知，与应力路径1相同，应力路径2，3，4条件下试件的卸载应力-应变曲线表现出与初始围压较强的相关性，即：围压越大，试件的偏应力越大；需要指出的是，无论应力路径2，3还是应力路径4，试件的应力-应变曲线趋势基本相同，特别在峰后阶段均表现出塑性流动，甚至应变强化现象；与传统应力路径( 应力路径1 )不同，应力路径2，3，4条件下，试件在卸载初期就表现出明显的应变曲线变化，越是接近失效状态，微小的围压就会导致巨大的轴向和径向应变；在3种应力路径中，应力路径2的试件径向应变最大，其次为应力路径3，最后为应力路径4，这可能是因为应力路径2中的轴向应力能够使径向应变增加更快，从而使试件能够吸收更多的外载荷能量。

2.2 卸压极限承载强度分析

在加载过程中，试件内部颗粒和结构不断出现损伤，因此不能使用试件加载过程中的峰值强度来研究卸载过程中的极限强度，引入卸压极限承载强度uq表征不同应力路径下卸载过程中的岩石承载能力，即卸压极限承载强度越大，岩石在卸载过程中能够承受的峰值应力越大，反之则越小。

采用增量法确定试件卸载过程中的卸压极限承载强度uq。图6为应力路径4中，在25 MPa围压条件下，试件卸载过程中轴向应变增量与偏应力比值和偏应力的关系。

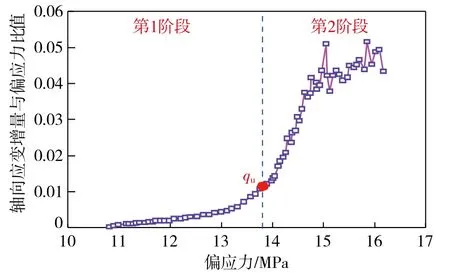
图6 卸载过程中轴向应变增量与偏应力比值和 偏应力的关系 Fig. 6 Relationship between ratio of axial strain increment to deviatoric stress and deviatoric stress during unloading

由图6可知，试件卸载过程中轴向应变增量与偏应力比值和偏应力的关系曲线可分为2个阶段。第1阶段，曲线逐渐上升，表明试件处于不稳定失效过程；第2阶段，曲线增涨速率激增，表明试件内部颗粒破坏并生成裂纹。因此，2个阶段的转化点即为卸载过程中试件的卸压极限承载强度。

为验证增量法所确定的卸压极限承载强度的合理性，在应力路径4中25 MPa围压条件下，绘制卸载过程中轴向应变增量与围压增量比值和围压的关系，如图7所示。由图7可知，试件卸载过程同样可分为2个阶段，以第1阶段和第2阶段产生的转化点确定此时的围压，再换算对应的卸压极限承载强度，其所获得的结果与之前相同，由此证实增量法可以用来确定试件卸压极限承载强度。

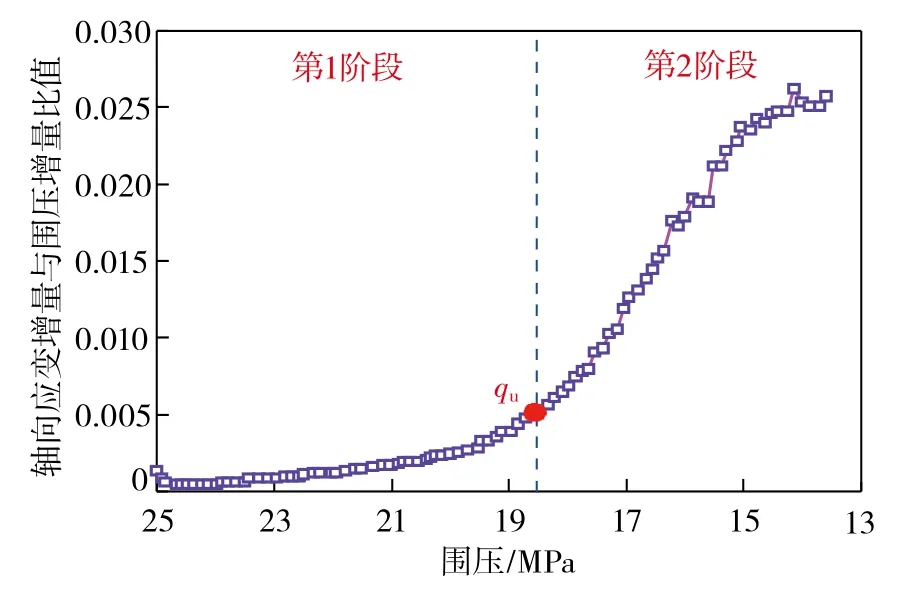
图7 卸载过程中轴向应变增量与围压增量比值和围压的关系 Fig. 7 Relationship between axial strain increment and confining pressure increment ratio and confining pressure during unloading

根据以上分析，绘制不同应力路径下试件的卸压极限承载强度，如图8所示。

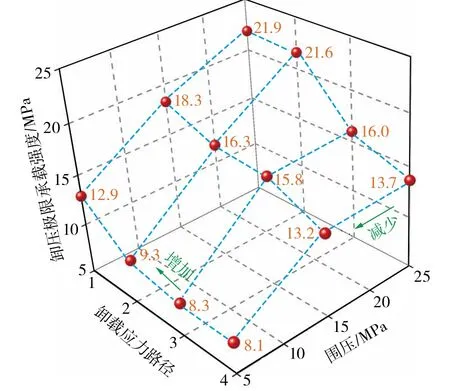
图8 不同应力路径下试件的卸压极限承载强度 Fig. 8 Ultimate load-bearing strength of specimen under different stress paths

由图8可知，在4种应力路径下，试件的卸压极限承载强度均随着围压的增加而增强，而应力路径2，3，4中的试件卸压极限承载强度均小于应力路径 1中的试件卸压极限承载强度，其中应力路径4中试件的卸压极限承载强度最低，应力路径3中试件的卸压极限承载强度稍好，应力路径2中试件的卸压极限承载强度较强。这表明当轴向和径向应力均减小时，软弱夹层泥岩的承载能力最弱。

2.3 卸压变形规律及膨胀特性

2.3.1 卸压变形规律

为进一步研究应力路径对试件应变的影响，绘制在应力路径2，3，4条件下卸压过程中试件的围压与应变的关系，如图9所示。

由图9可知，卸载初期径向应变与体积应变就出现增加，在应力路径2( 轴向应力增加，径向应力减小 )条件下，试件应变变化尤为明显。

图9 不同应力路径下卸压过程中试件的围压与应变的关系 Fig. 9 Relationship between confining pressure and strain of specimen during pressure relief under different stress paths

本文引入卸压应变率3σεΔ˙i研究卸载过程中总应变的演化规律。

式中，εΔi(i=1，3，v)分别为开始卸载至试件失效过程中的总轴向应变增量、总径向应变增量和总体积应变增量；3σΔ 为该过程中对应的围压变化量。

可以看出，卸压应变率不仅可以用来表征卸载过程中软弱夹层泥岩所受围压对变形量的影响，同时还可用来描述软弱夹层泥岩在不同应力状态下应变的响应速率，即卸压应变速率越大，试件的轴向应变、径向应变和体积应变对围压的变化越敏感。

表2和图10为应力路径2，3，4条件下，卸压应变速率与卸压初期围压的关系。

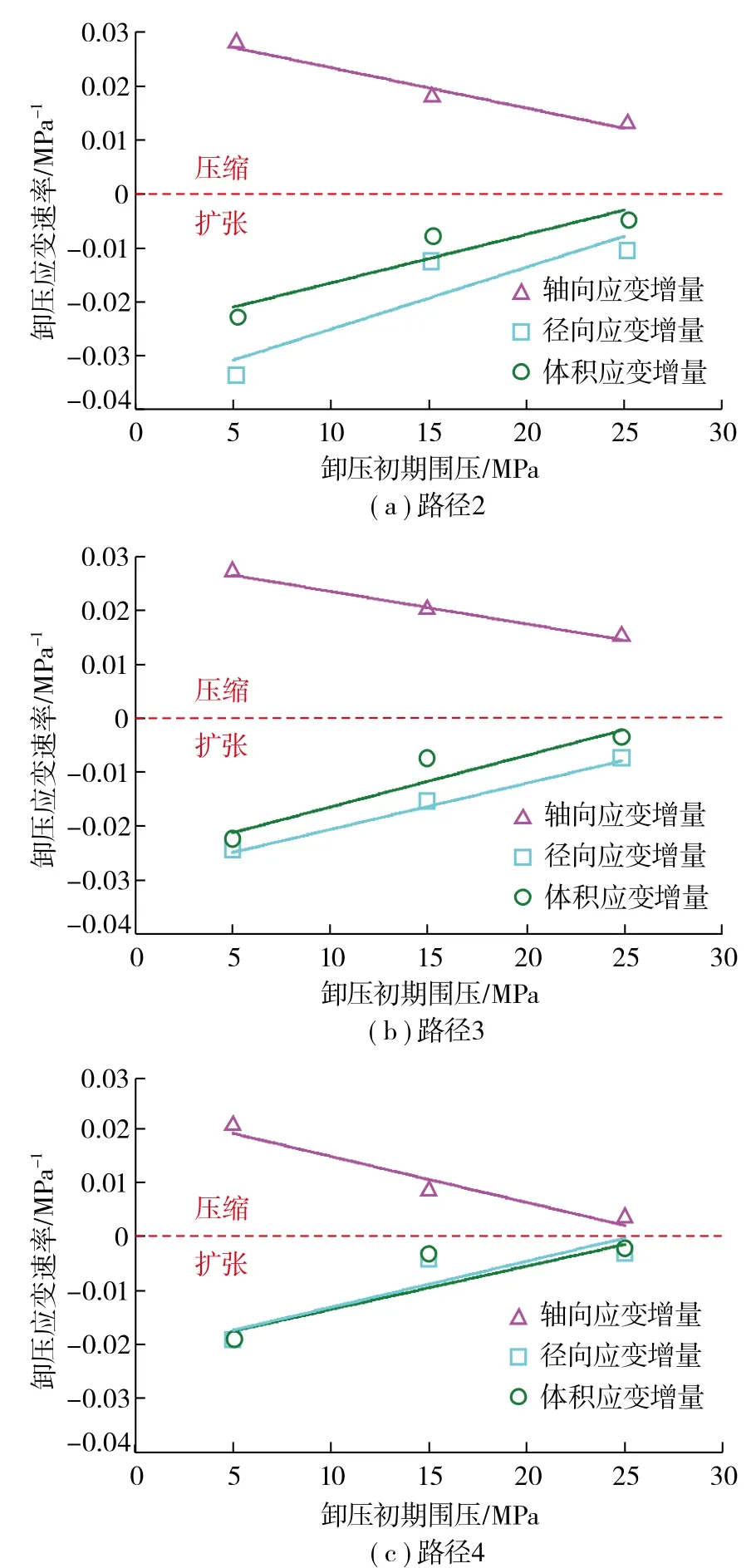
图10 卸压应变速率与卸压初期围压值的关系 Fig. 10 Relationship between pressure relief strain rate and initial confining pressure

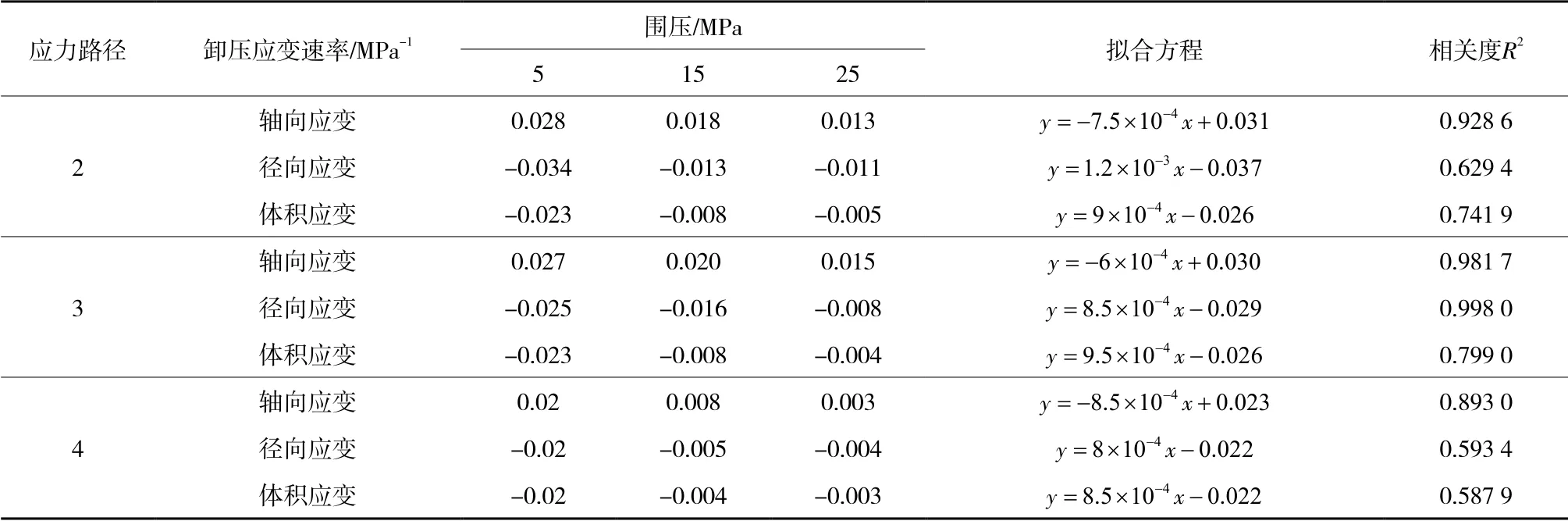
表2 卸压应变速率与卸压初期围压的变化关系 Table 2 Variation relationship between pressure relief strain rate and initial confining pressure

由图10可知，不同应力路径下试件轴向、径向和体积应变增量随卸压初期围压的变化规律基本相同，随着卸压初期围压的增加，试件轴向、径向和体积应变增量均减小，这是因为较大的围压会抑制试件应变的增加。

2.3.2 弹性模量和泊松比变化规律

由胡克定律可知，对于三轴状态下弹性体的轴向和径向应变可表示为

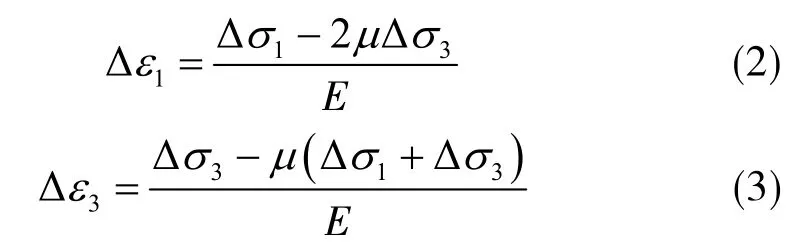
经换算，弹性模量E与泊松比μ可表示为

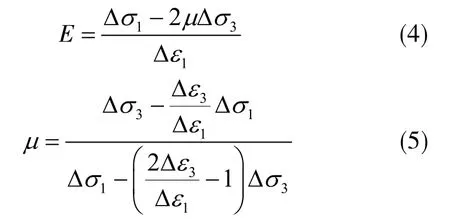
考虑到初始围压和卸载过程均影响变形参数恶化程度的标定，因此引入卸载应力率H研究不同卸载应力路径下变形参数的演化规律。

式中，，σ3分别为应力路径下初始围压和某个卸载过程中的卸载围压。

图11，12分别为不同应力路径条件下试件弹性模量和泊松比与卸载应力率的关系。

由图11可知，在不同应力路径下，随着卸载应力率的增加，软弱夹层泥岩的弹性模量呈近直线降低，表明由于内部颗粒的破碎、结构裂隙的扩展和 破坏，使得软弱夹层泥岩性能出现恶化现象，同时弹性模量的恶化程度可用一次方程进行拟合表征。

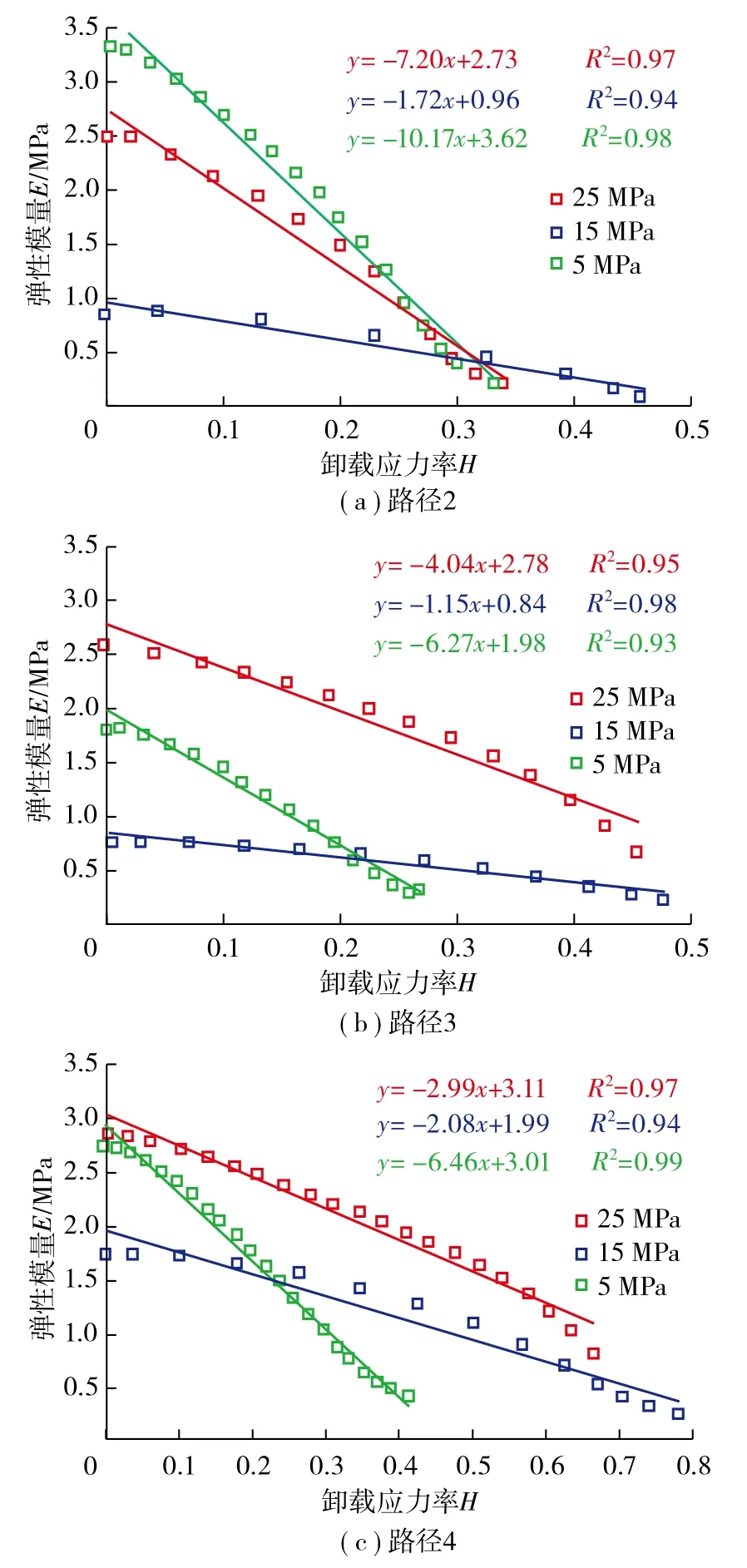
图11 弹性模量与卸载应力率的关系 Fig. 11 Relationship between elastic modulus and unloading stress rate

由图12可知，在不同应力路径下，随着卸载应力率的增加，由于试件轴向裂纹的扩展，使得试件的径向变形增加，导致软弱夹层泥岩的泊松比单调增加，这种泊松比增涨趋势可用二次方程进行拟合表征。

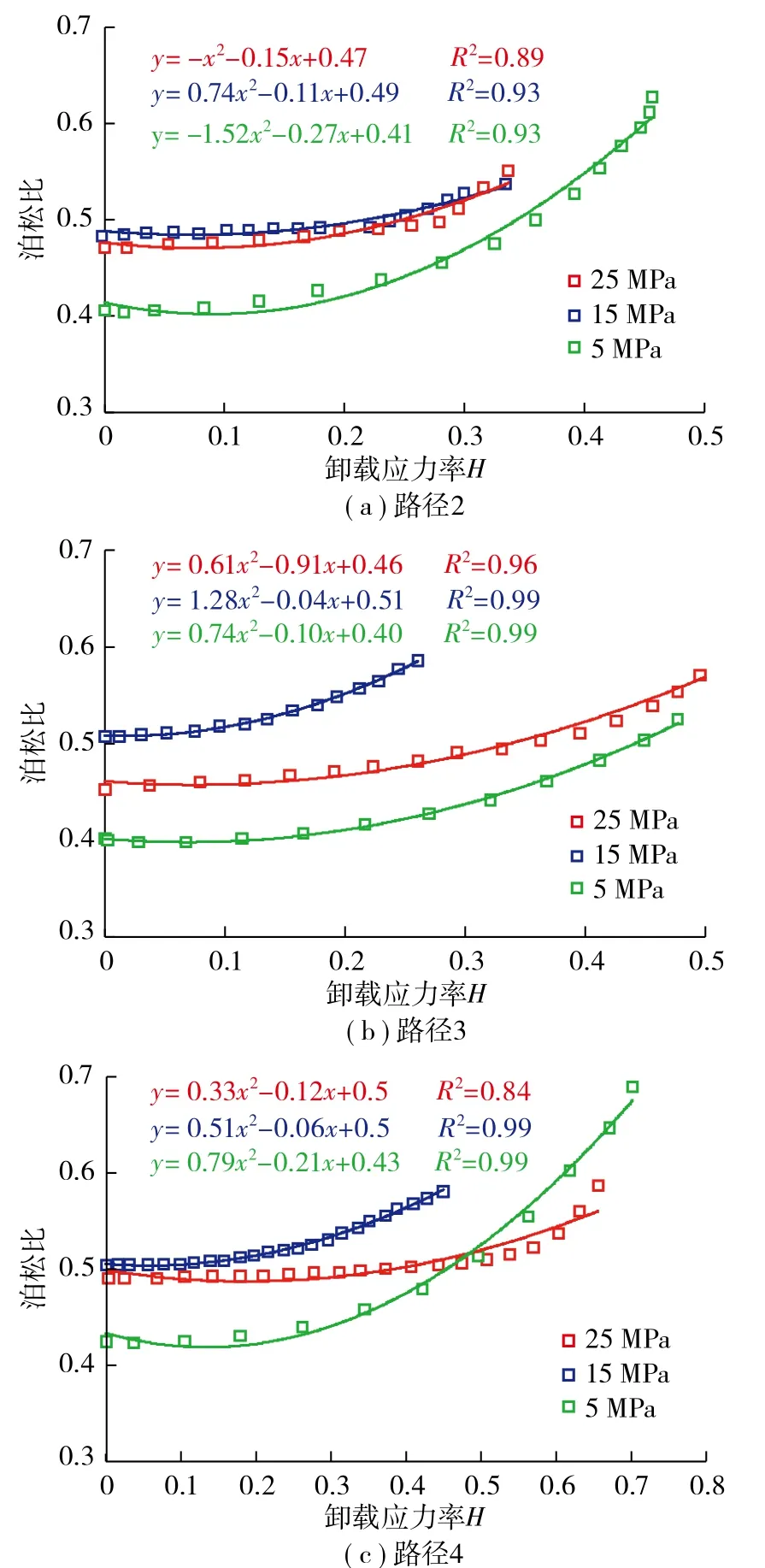
图12 泊松比与卸载应力率的关系 Fig. 12 Relationship between Poisson's ratio and unloading stress rate

为进一步研究不同应力路径下软弱夹层泥岩弹性模量和泊松比的恶化程度，引入弹性模量恶化率Δ˙E和泊松比恶化率μΔ˙，表达式如式( 7 )，( 8 )所示。相同卸载过程中，弹性模量恶化率越大，试件 的弹性模量减小程度也越大，而软弱夹层泥岩的强度削弱程度也越大，反之则越小。泊松比恶化率的变化规律与其相同。

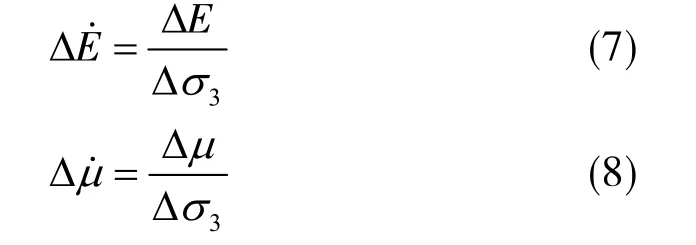
式中，ΔE，μΔ 分别为不同应力路径下弹性模量增量和泊松比增量。

表3为不同应力路径和围压条件下试件的弹性模量恶化率和泊松比恶化率。

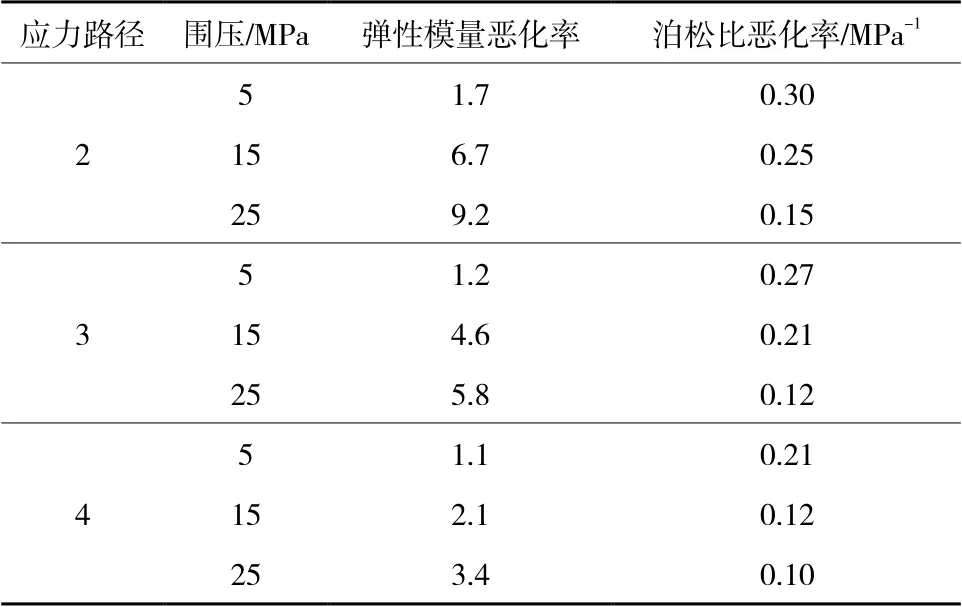
表3 不同应力路径和围压条件下试件的弹性模量恶化率和泊松比恶化率 Table 3 Deterioration rate of elastic modulus and Poisson's ratio of specimens under different stress paths and confining pressures

图13，14分别为不同应力路径和围压条件下试件弹性模量恶化率和泊松比恶化率的变化规律。

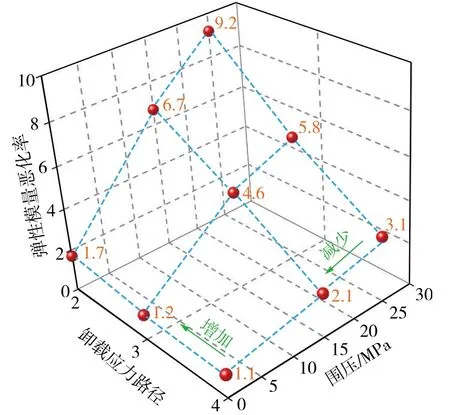
图13 不同应力路径和围压条件下弹性模量恶化率 Fig. 13 Deterioration rate of elastic modulus under different stress paths and confining pressures

由图13可知，在卸载过程中，弹性模量恶化率随初始围压的增加而增高，说明在更大的初始围压条件下，试件的弹性模量降低会更显著，软弱夹层泥岩会更早地开始储存能量。其中，在应力路径2中试件的弹性模量恶化率最大，其次为应力路径3，而应力路径4中试件的弹性模量恶化率最小，说明在相同初始条件下，增大轴向应力的同时减小径向应力将使得软弱夹层泥岩的强度削弱最大。

由图14可知，与弹性模量恶化率相同，应力路径2中试件的泊松比恶化率最大，其次为应力路径3，而应力路径4中试件泊松比恶化率最小。因此，在较低的围压条件下，软弱夹层泥岩的泊松比恶化率更大，这表明低围压时，软弱夹层泥岩的泊松比变化更快，对围压的改变更加敏感。

图14 不同应力路径和围压条件下泊松比恶化率 Fig. 14 Deterioration rate of Poisson's ratio under different stress paths and confining pressures

综上所述，在卸载过程中，软弱夹层泥岩的弹性特征符合恶化规律，且应力路径2对软弱夹层泥岩变形特征影响最大。

3 结 论

( 1 ) 随着围压的增加，软弱夹层泥岩逐渐呈现塑性流动特征，当围压达到15，25 MPa时，软弱夹层泥岩出现应变强化现象。

( 2 ) 应力路径对软弱夹层泥岩应力-应变曲线呈现趋势影响较小，但增加轴向应力同时减小径向应力会大大增加软弱夹层泥岩的径向应变。

( 3 ) 卸压极限承载强度指标可较好地表征不同应力路径卸载过程中的岩石承载能力。卸压极限承载强度越大，岩石在卸载过程中能够承受的峰值应力越大，反之则越小。

( 4 ) 较大的围压会抑制软弱夹层泥岩应变的增加。在卸载过程中，软弱夹层泥岩的弹性模量和泊松比恶化程度可分别用一次、二次方程进行表征。