矿井地下水库破碎岩体运移的DEM-CFD耦合分析

张 村，宋子玉，赵毅鑫,，韩鹏华，滕 腾

( 1. 中国矿业大学( 北京 ) 共伴生能源精准开采北京市重点实验室，北京 100083；2. 中国矿业大学( 北京 ) 能源与矿业学院，北京 100083；3. 安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001)

近年来我国煤炭去产能战略持续推进，煤炭主产区由东部地区逐渐向西部转移，西部矿区千万吨级别高强度开采矿井大量涌现。但西部矿区气候干燥，蒸发量是降雨量的6倍左右。再加之西部矿区高强度的开采，对本已脆弱的西部矿区生态水环境造成严重影响[1-2]。据统计，中国每年因煤炭开采破坏地下水约80亿t，而利用率仅25%左右，损失的矿井水资源相当于中国每年工业和生活缺水量( 100亿t )的60%[3]。因此，如何实现煤炭开发与水资源保护相协调，是西部煤炭科学开发的重大难题之一，也是矿区生态文明建设的核心内容。据此，顾大钊院士[3]提出了煤矿地下水库的概念和矿井水井下储存利用的理念与技术。目前该技术在神东矿区应用，已建成35座煤矿地下水库，储水量2 500万m3，供应了矿区95%以上的用水，并为周边产业供水，有助于西部矿区煤炭开采水资源保护利用。

矿井地下水库建设过程中，矿井采空区储水能力和矿井地下水库稳定运行是关键科学问题[3]。由于垮落带孔隙率高、渗透率大，是矿井地下水库最主要的库容体，垮落带的孔隙演化规律直接影响矿井水库的储水能力[4-7]。垮落带又作为矿井地下水库的主要承载体，与残留煤柱协同承载着上覆岩层的载荷确保矿井水库稳定运行[8-9]( 图1 )，垮落带破碎岩体遇水弱化导致覆岩下沉同样影响着矿井水库的储水能力。垮落带储水能力的减小，将导致矿井地下水库水位大幅度提升，威胁矿井地下水库的稳定性。因此，垮落带破碎岩体在矿井水库运行过程中孔隙演化规律是影响矿井水库储水能力的重要因素。

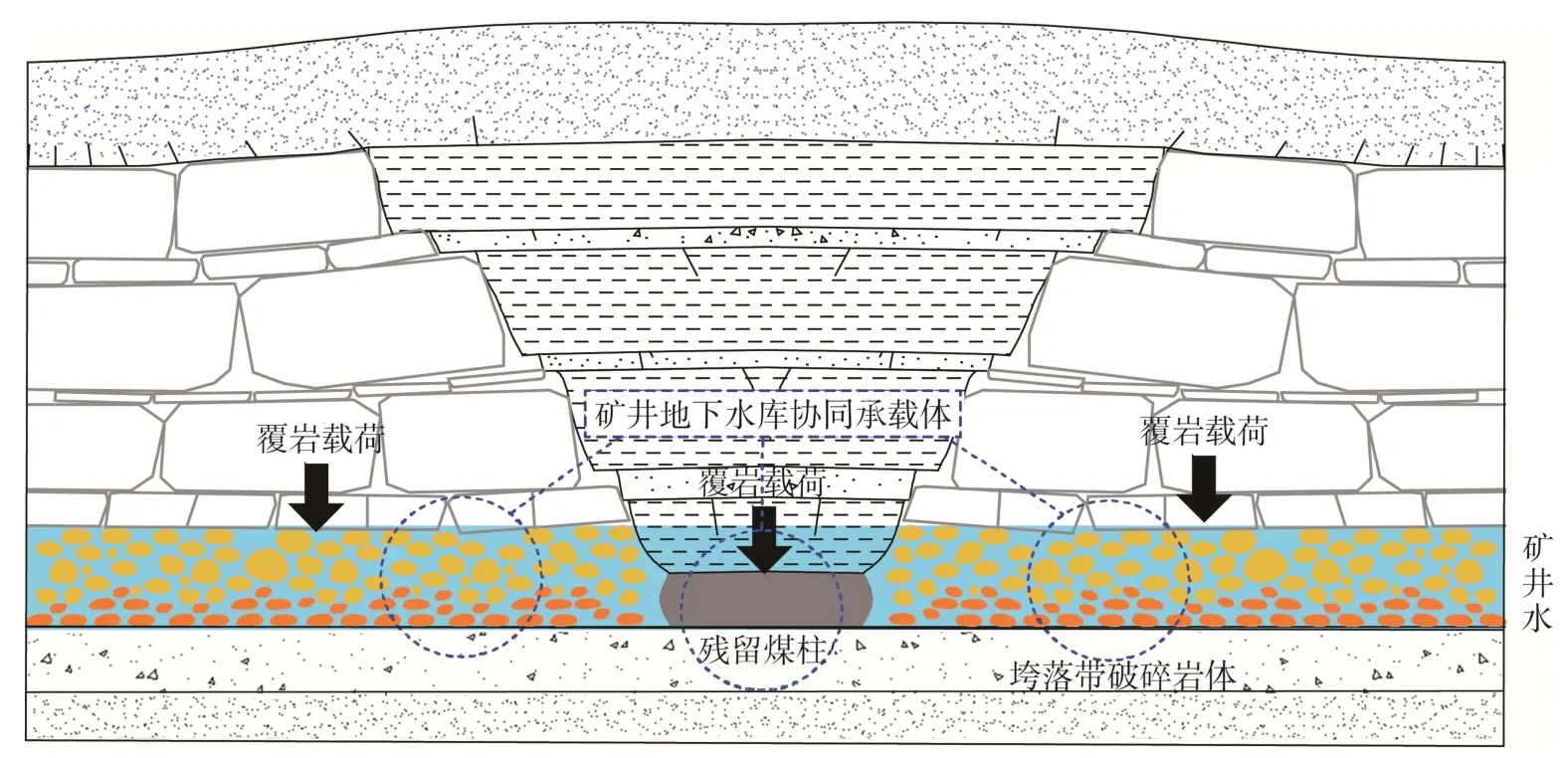
图1 矿井地下水库垮落带+残留煤柱协同承载结构 Fig. 1 Collaborative bearing structure of caving zone of mine underground reservoir and residual coal pillar

采空区垮落带可以视为由破碎岩体组成的多孔介质，随着工作面的持续推进，造成上覆岩层的不断下沉压实采空区垮落带，垮落带自身的应力、密度、孔隙率、渗透率等参数均会发生变化[10]。在采空区作为矿井水库过程中，垮落带破碎岩体将长期处于水浸受载环境中，水岩作用下破碎岩体受载内部结构劣化、损伤演化规律复杂多变[11-13]。在矿井地下水库运行过程中，破碎岩体主要发生受载破碎( 再次破碎和结构调整 )、水浸软化( 侵蚀溶解和遇水膨胀 )以及水渗冲蚀( 冲蚀扩孔和小破碎岩体携带 )等耦合损伤( 图2 )，进而造成破碎岩体再次破碎、孔隙结构调整和压实变形，使得垮落带孔隙空间大幅度减小，降低矿井水库储水能力。

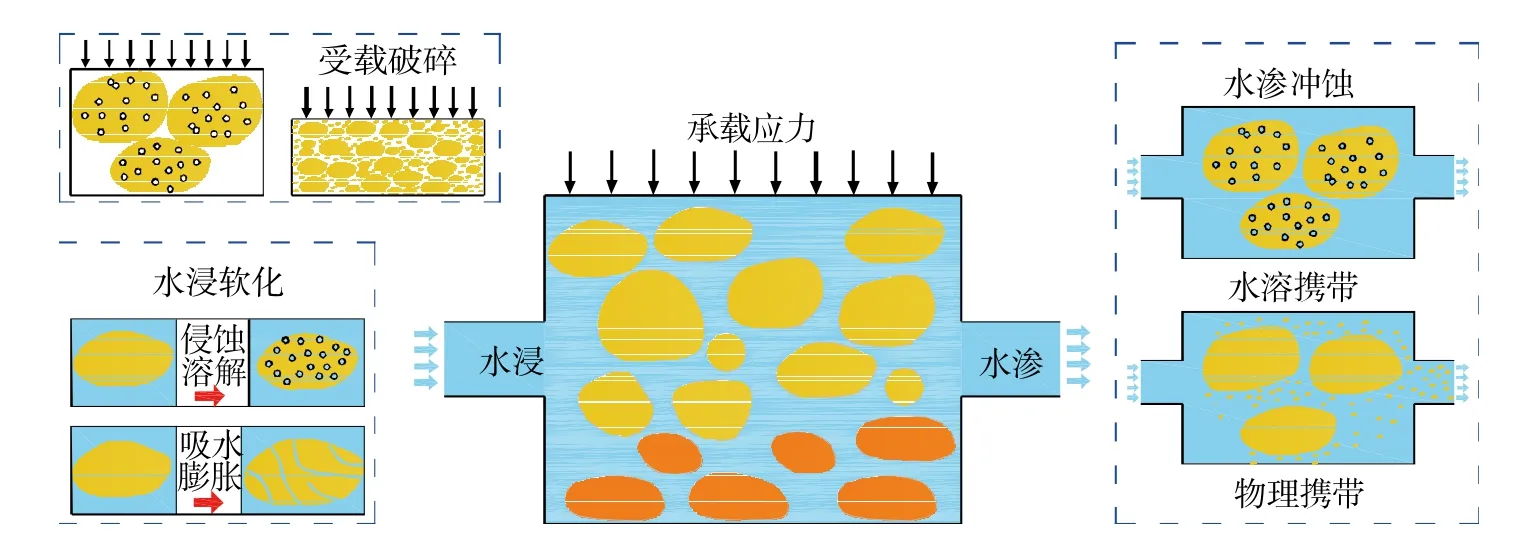
图2 破碎煤岩体耦合损伤与孔隙空间变化情况 Fig. 2 Coupling damage and pore space changes of broken coal and rock mass

对于垮落带破碎煤岩体的压实破碎特征，学者们[14-20]采用实验室测试和数值模拟进行了大量的研 究，主要考虑破碎煤岩体粒径大小、形状、强度、水分、风化程度等因素对压实及渗流特征的影响，主要表现为：① 在压实过程中破碎岩体的干密度逐渐升高；② 破碎岩体弹性模量随着压实应力的增加而线性增加，饱和含水状态下弹性模量的增加速度更快，但不会超过其完整状态下的弹性模量；③ 随着应力的不断升高，破碎岩体大小的分形维数将趋于一个固定值，该值与破碎岩体初始粒径及强度有关。在破碎岩体初始粒径及压实应力相同的情况下，分形维数随着破碎岩体强度的增加逐渐减小。煤矿开采过程中涉及水岩作用的研究主要集中在顶底板突水、巷道围岩遇水稳定性、断层陷落柱突水以及工作面注水防片帮等方面[21-22]。为了获得煤岩体遇水强度弱化的细观机理，李桂臣[23]、邓华锋[24]等借助CT和离散元数值模拟进行煤岩体遇水细观劣化机制的研究。除此之外，很多学者[25-29]根据采动应力和水环境效应研究动静载、加卸载、水化学侵蚀等条件下浸水煤岩体物理力学性质的演化特征。但是到目前为止，对于矿井地下水库循环储放水过程中水体渗流对垮落带孔隙率的影响研究相对较少。矿井储放水过程中由于储水高度不一致，水流速度存在差异。采空区垮落带内破碎岩体尺寸范围大，从粉末颗粒到直径数米的破碎岩体均存在。除此之外，采空区垮落带由于压实程度不一致，采空区中部孔隙率要小于四周，同样影响矿井水渗流过程中对破碎岩体的携带作用，进而影响采空区垮落带的孔隙率。

据此，笔者通过理论分析，建立矿井水渗流与破碎岩体耦合作用方程，探讨垮落带孔隙率、破碎岩体尺寸以及矿井水流速对破碎岩体的携带作用的影响。最后将理论模型嵌入至PFC3D中，采用DEM-CFD耦合程序模拟分析了流速对破碎岩体孔隙率的影响，研究结果有助于掌握矿井水渗流过程中垮落带孔隙率的演化规律。

1 流固耦合控制方程

1.1 流固耦合作用原理

通过附加力考虑颗粒与流体的相互作用，根据矿井地下水库液体流动情况可知，主要为水平流动迁移，假设研究区域为位于流体内部的破碎岩体，其在矿井地下水库的受力条件可以简化成如图3所示的应力环境，则有

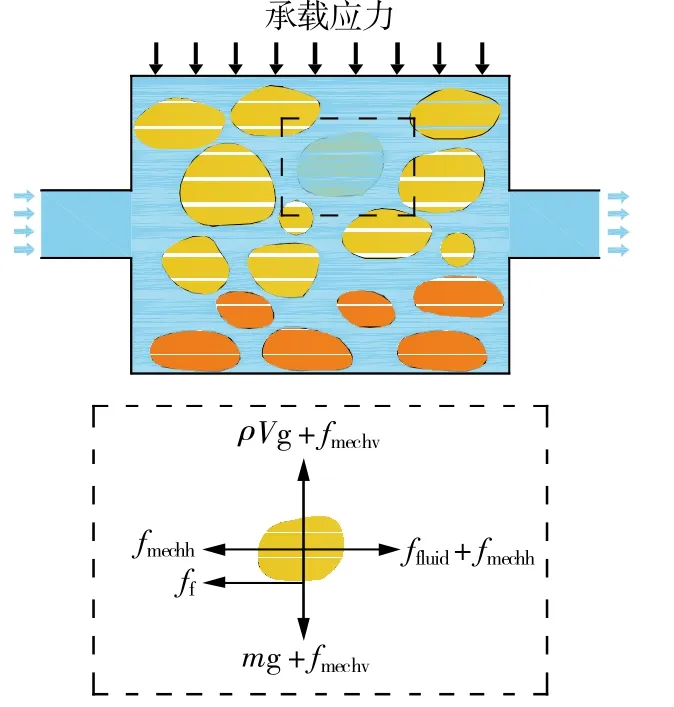
图3 矿井地下水库破碎岩体受力条件 Fig. 3 Stress condition of broken rock mass in underground reservoir of mine

式中，为颗粒速度；m为颗粒质量；为流体施加在颗粒上的总作用力( 流固耦合相互作用力 )，其由拖曳力和流体压力梯度导致的力组成为作用在颗粒上的水平外力( 主要为颗粒间的水平接触力 )之和；为重力加速度；Vm为颗粒体积；ρf为流体密度；为作用在颗粒上的垂直应力( 主要由上覆岩层施加的力 )之和；μm为颗粒摩擦因数，进而求出摩擦力ff；为颗粒角速度；I为惯性矩；为作用在颗粒上的力矩。

流体作用于颗粒的拖曳力是基于包含该颗粒的流体单元自身条件为其单独定义的。需要说明的是，流体-颗粒相互作用力默认施加在颗粒形心上，并且没有转矩作用。因此拖曳力[30]计算公式为

这个校正项使这个力同时适用于高孔隙率和低孔隙率系统，并且支持雷诺数的大范围取值[31-32]。单个颗粒所受拖曳力被定义为

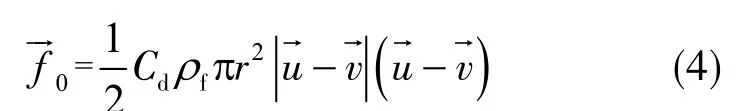
式中，Cd为拖曳力系数，由式( 5 )计算；r为颗粒半径；→为流体流速。

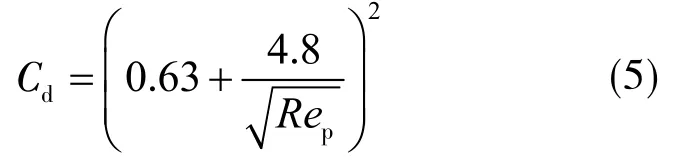
式中，Rep为颗粒雷诺数，进而经验系数χ[32]的计算公式为

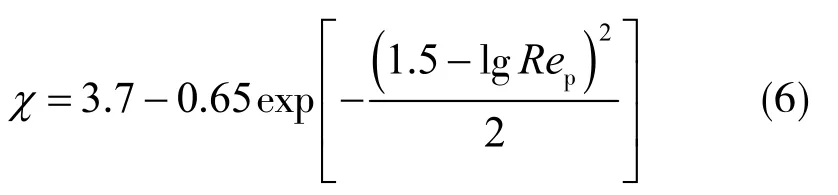
颗粒雷诺数可以表示为

式中，μf为流体的动力黏滞系数。

式中，p为流体压力。

1.2 渗流求解方程

由于矿井水库储放水过程中水体体积较大，水体流动流速相对较小，多孔介质中的低雷诺数流体可由达西定律描述。需要说明的是，达西定律对应的雷诺数上限在1～10之间，与多孔介质的粒径存在一定的关系：

式中，K为渗透率。

这里假定流体的压缩性小到可以忽略，通过隐式求解可以根据流速很快得出流体的压力场。为了考虑流体流动受颗粒的影响，渗透系数由多孔介质模型的孔隙度计算。本文采用Kozeny-Carman方程计算渗透系数：

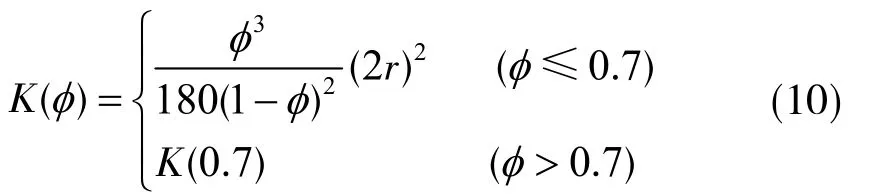
式中，为了计算渗透系数，同时考虑矿井水库条件，孔隙率上限设置为0.7，孔隙率超过0.7则渗透系数取常数。

上述是针对低雷诺数的达西流渗流方程，当雷诺数超过10时，达西流不再适用，此时多孔介质中的渗流可用Forchheimer公式进行描述：

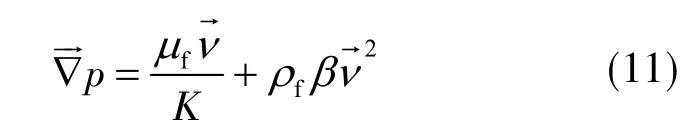
式中，β为非达西渗流因子。

为了简化计算，本文主要还是以达西渗流为主进行分析。

2 影响因素分析

2.1 垮落带孔隙率

为了方便计算，本文采用表1中的数据进行计算，同时假设颗粒的初始速度为0，将表1中的数据代入式( 8 )，依据本计算案例获得的孔隙率与流体对颗粒的作用力的关系见式( 12 )，孔隙率由0～0.7下的流体对颗粒的作用力如图4所示。为了实现正负值的统一，在下文分析中，统一将颗粒运动方向的力设为正。

表1 模型计算参数 Table 1 Model calculation parameters

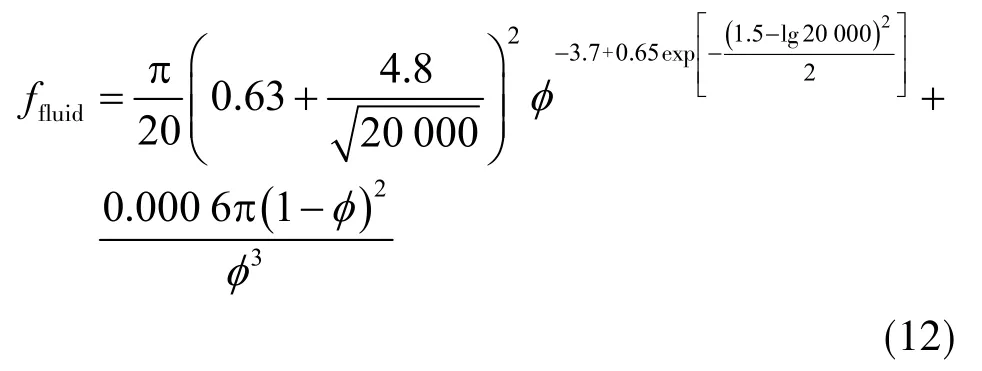
由图4可以看出，破碎岩体所受流体压力大小随着孔隙率的增加急剧减小，在孔隙率逼近0时，流体压力逼近无穷大。在孔隙率由0.1达到0.3时，流体压力由338 N降至5.9 N，孔隙率升高至0.7时，流体压力降至0.26 N。除此之外，由于拖曳力/流体压力的比值K约等于1，因此，梯度力基本可以忽略不计。水中矸石颗粒的静摩擦因数设为0.49[33]，在考 虑浮力且不考虑垮落带上覆压力和接触力的情况下，颗粒加速度a的计算公式为

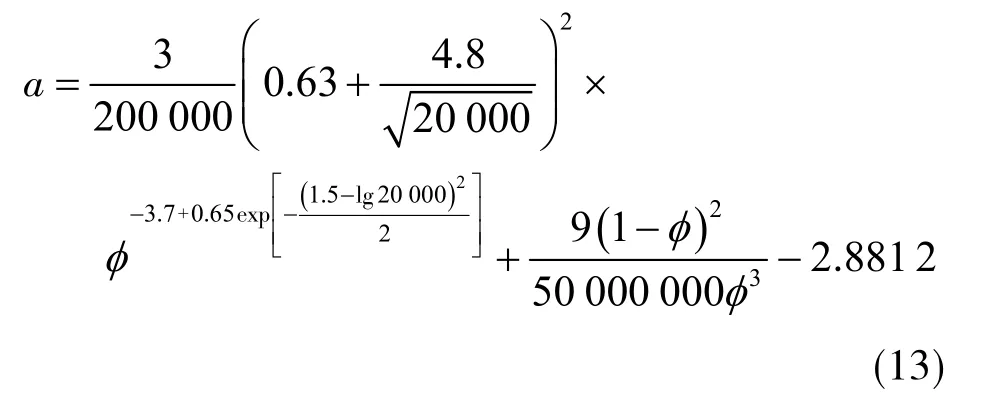
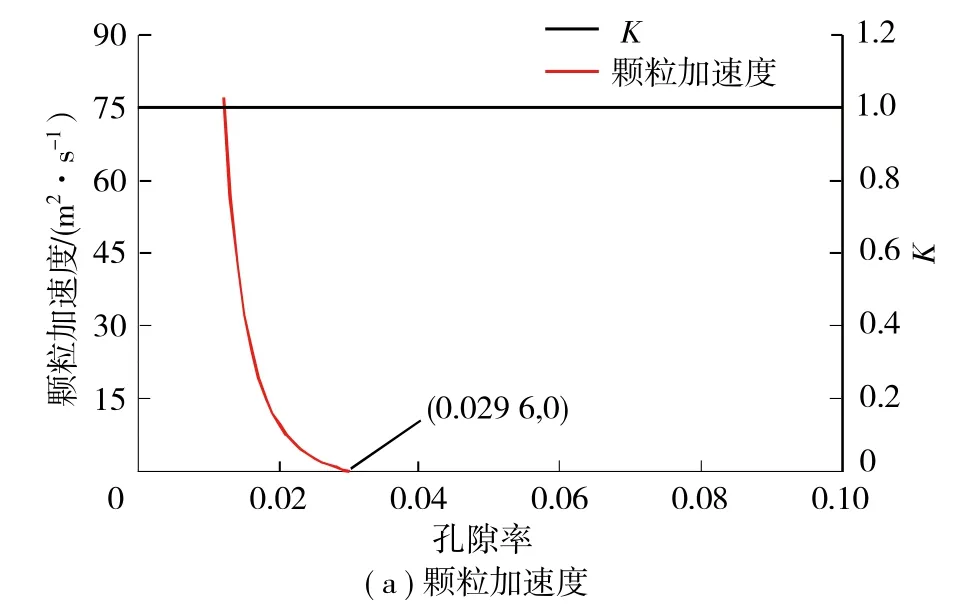
图4 多孔介质颗粒加速度及流体压力与孔隙率的相关关系 Fig. 4 Relationship between particle acceleration and fluid force and porosity of porous media

由式( 13 )可以看出，孔隙率只影响流体压力部分导致的加速度，因此，只有当流体压力大于摩擦力时，破碎岩体颗粒才能运移。结合式( 13 )及图4可以看出，在表1条件下，加速度与流体压力变化趋势一致，只有当垮落带孔隙率为0.029 6时，颗粒才能被携带移动。结合采空区垮落带实际孔隙率范围( 随着压实程度的不同，在0.3～0.6之间[10])，表明在表1条件下，破碎岩体不会被流体携带走。在这种情况下，则需要考虑破碎岩体粒径以及流速对流体压力的影响。

2.2 破碎岩体尺寸

采空区垮落带破碎岩体分布尺寸差异巨大，从粉末状的毫米级到岩体的米级均存在。因此，有必要探索岩体尺寸对流体压力的影响情况。在表1条件下，岩体尺寸分别与流体压力和颗粒加速度的关系如式( 14 )和( 15)所示，对应的曲线如图5所示。

图5 流体压力及颗粒加速度与破碎岩体尺寸的相关关系 Fig. 5 Relationship between fluid pressure and particle acceleration and particle size

由图5可以看出，虽然岩体尺寸的增加使得岩体所受流体压力呈幂函数上升，但由于破碎岩体半径的增加同样使得破碎岩体质量大幅度增加，导致总体上破碎岩体尺寸越大，破碎岩体加速度下降越快。在流体速度为0.01 m/s时，只有破碎岩体半径为0.000 48 m的破碎岩体能被携带走。如果再考虑上覆岩层的应力和破碎岩体之间的接触力，流体速度为0.01 m/s时，基本携带不了破碎岩体，只能携带破碎岩体孔隙空间的粉尘。上述计算是在孔隙率为0.5的情况下获得的，垮落带中部孔隙率相对于垮落带边界要低得多。因此，如果相同条件下，孔隙率为0.3时，粒径为0.001 34 m的破碎岩体将被流体携带，同样很小。对于破碎岩体半径变化过程中的拖曳力和梯度力而言，流体压力中的拖曳力仍占绝对优势，拖曳力占流体压力的比值K维持在1，压力梯度力同样可以忽略不计。

2.3 矿井水流速

除了垮落带自身粒径和孔隙率以外，流体流速同样影响垮落带内能被流体携带的岩体尺寸，图6是在表1条件下，垮落带内流体压力及加速度与流体流速的关系( 式( 16 )～( 17 ) )。流速的增加使得流体携带破碎岩体的能力加大。半径为1 m的破碎岩体，在流速达到1.925 m/s时，也能达到启动加速度。而假设垮落带破碎岩体最大半径达到10 m，则同等条件下流速需要达到6.1 m/s才能使得不考虑覆岩压力和破碎岩体接触力的岩体发生流动。同样的，由图6可以看出，流体压力中拖曳力占主导，梯度力可以忽略不计。

图6 流体压力及颗粒加速度与流体速度的相关关系 Fig. 6 Relationship between fluid pressure and particle acceleration and fluid velocity

3 数值模拟分析

笔者通过理论分析可以看出，矿井地下水库在蓄放水过程中对垮落带岩体将会产生携带作用，但在分析过程中并没有考虑破碎岩体间的接触力对破碎岩体运移的影响，也无法掌握整个垮落带孔隙率的演化情况。因此，为了更加直观地分析流体运移对垮落带孔隙率的影响特征，笔者采用DEMCFD流固耦合模拟方法进行实验室尺度的流固耦合模拟。

3.1 流固耦合实现方法

笔者采用PFC3D进行模拟，PFC3D中内置了计算流体动力学( CFD )模块，能够在PFC3D中分析流固耦合作用问题，但PFC3D中不包括CFD求解器，只提供了与CFD软件连接的命令和脚本函数，需要与其他软件进行同步分析。

3.1.1 孔隙率计算

有2种方法可用于计算流体单元的孔隙率，采用表征颗粒的中心位置或多面体，即中心法和多面体法。本文采用计算效率更快的中心法，中心法适用于颗粒完全包含于该流体单元中，因此需要对流体网格和颗粒尺寸进行限制。流体单元零孔隙度的产生会导致流体控制方程中产生奇点( 式( 3 )，拖曳力会无穷大 )，为了避免由奇点引起的问题，本文限制流体单元的孔隙率不小于0.005。需要注意的是，流体单元孔隙率计算采用整个颗粒的体积，未对重叠部分进行修正，这就造成低孔隙率多孔介质的流体孔隙率要略大于实际孔隙率。

3.1.2 流体网格尺寸

PFC3D中CFD模块支持全部由四面体或全部由六面体组成的网格。六面体单元表面必须是平面。为了解决流动结构问题，流体网格需要满足以下不等式：

式中，dc为流域最小宽度；Δxcfd为流体单元长度。

由于上述耦合方法用于描述在一个流体单元中发生的平均耦合力。因此假定局部的孔隙度均匀分布在1个单元内，颗粒周围的流动并没有被明确地表示出来。为了得到好的结果，1个CFD单元中应该包含若干个PFC3D颗粒，即

3.1.3 耦合实现

当CFD模块激活时，流体-颗粒相互作用力在PFC周期序列中被施加到颗粒上。PFC3D循环计算过程中，流体-颗粒相互作用力和每个流体单元的孔隙度依据给定的时间间隔重复计算。在模拟过程中可以强制更新上述变量，也可以开启和关闭耦合模式。流体力学双向耦合是通过流体求解器和PFC3D之间进行一系列数据交互实现的。每个流体单元的孔隙度取决于PFC3D。每个流体单元体积的体积力由PFC3D决定。每个流体单元中的流体速度、流体压力、流体压力梯度、流体密度、流体动力黏滞系数都由流体软件决定。

CFD模块自动为PFC颗粒施加流体-颗粒相互作用力。双向耦合通过在流体流动模型中更新孔隙率和渗透率，在PFC的CFD模块更新流体速度场来实现。模型中设定每隔一定步数的力学周期更新稳态流场。与流体求解软件同步和数据交换可以通过FISH或Python脚本中的TCP套接字通信实现。

3.2 数值模拟构建

为了提高计算效率，本文的模拟尺度为实验尺度，模型横截面尺寸为0.1 m×0.1 m，长度为0.2 m，模型四周为不渗透墙体。模型入口处渗流速度分别设为0.5，1和2 m/s，出口处设置压力为0。模型中破碎岩体半径分为2组，分别为0.001和0.003 m，占比分别是10%和90%，共31 830个球体。流体单元采用立方体模型，边长为0.02 m，符合上述尺寸要求。具体模型如图7所示。

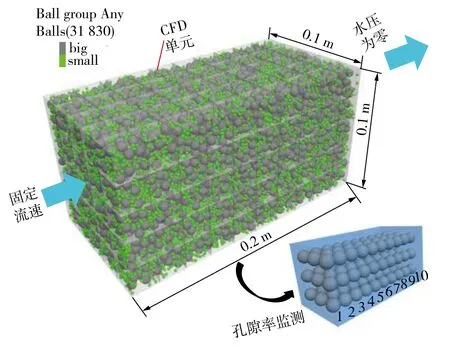
图7 DEM-CFD渗流模型及孔隙率监测点布置 Fig. 7 DEM-CFD seepage model and arrangement of porosity monitoring points

模拟过程中，为了考虑破碎岩体形状对破碎岩体流动的影响，破碎岩体接触模型采用滚动阻力线性模型( Rolling Resistance Linear Model )，模拟参数见表2。为了量化分析岩体不同位置处破碎岩体孔隙率的演化特征，在破碎岩体内部布置了10组，每组9个的监测单元，具体如图7所示。

表2 破碎岩体接触参数[33] Table 2 Particle contact parameters[33]

3.3 模拟结果分析

根据模拟结果分别绘制了孔隙率监测单元第1层，中间第5层以及最后1层孔隙率的演化规律，具体如图8所示。

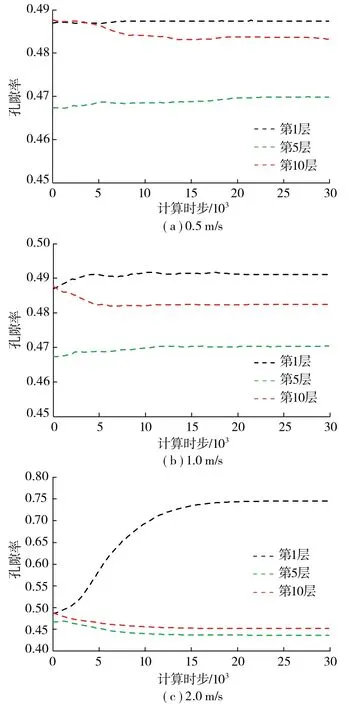
图8 不同流速模型孔隙率的演化规律 Fig. 8 Evolution of porosity in different flow velocity models

不同渗流速度条件下的破碎岩体位移、接触力以及拖曳力如图9所示。

根据理论分析可知，在流体速度分别为0.5，1.0和2.0 m/s，破碎岩体在不考虑上覆压力和破碎岩体之间接触力的情况下，1 mm半径的破碎岩体加速度分别能够达到272.4，1 002.7和3 767.1 m2/s；3 mm半径的破碎岩体加速度分别能够达到77.6，302.0和1 166.3 m2/s。可以看出在模拟条件下，如果单个破碎岩体被流体携带速度会很大。但模型内充满了破碎颗粒，且模型末端设有墙体，存在反向作用力，这就导致颗粒并不能大规模地被流体携带，具体如图9所示。由图8孔隙率的演化规律同样可以看出，流体速度为0.5和1 m/s时，模型的孔隙率变化幅度非常小，结合图9颗粒的位移情况，只存在与大颗粒孔隙间的小颗粒发生位移。对于大颗粒而言，一方面同等条件下大颗粒的加速度本来就要小于小颗粒；另一方面，大颗粒由于直径相对较大，颗粒配位数大，成为模型的骨架，接触应力相对较大( 图8 )。这就导致在流体速度为0.5和1.0 m/s时，大颗粒的位移基本为0。只有在流体速度达到2.0 m/s时，由于拖曳力明显增加( 图9 )，使得外侧大小颗粒均向内挤压，外侧孔隙率大幅度增加，这由图8( c )可以看出。

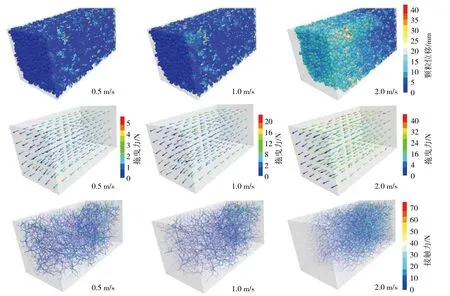
图9 不同流速破碎岩体位移、拖曳力以及接触力情况 Fig. 9 Particle displacement，drag force and contact force at different flow rates

对于不同渗流速度而言，主要改变的是流体对于破碎岩体的拖曳力( 梯度力可以忽略不计 )，在流速由0.5 m/s上升到1.0 m/s时，拖曳力大幅度增加，但拖曳力增加的同时，破碎岩体之间的接触应力同样增加，并不能打破原来的平衡结构，只能使得游离于结构之外的小颗粒岩体向内部运移，造成外部的孔隙率稍微增大，且流体速度越大，小颗粒岩体运移越多，孔隙率增加越快。在流速上升到2.0 m/s时，大颗粒岩体结构被冲破，向内部挤压，导致模型内部接触应力大幅度提升。这使得外侧的孔隙率大幅度提升，内侧孔隙率逐渐减小，进而影响模型的整体渗透率。模拟结果揭示了破碎煤岩体水渗流过程中内部破碎岩体迁移的过程以及孔隙率的演化情况。

4 展 望

在采空区垮落带内，破碎岩体不仅受到自身重力与水中浮力的影响，最主要的是受到上覆岩层的压实应力的影响，而在压实应力的作用下，破碎岩 体启动的拖曳力大幅度上升。因此，后期需要研究考虑压实应力条件下的流体渗流特征。同时，采空区垮落带破碎岩体的粒径分布范围更广，后期由实验室尺度扩展至工程尺度( 扩尺度 )的模拟是更好地服务工程应用的基础。而目前采空区扩尺度模拟首先需要解决的是垮落带破碎岩体的级配设置以及模拟的计算效率问题。

此外，在模拟过程中并未考虑水流携带走的部分小颗粒，也没有考虑蓄放水过程中水压的变化。但本文的模拟方法能够根据垮落带真实岩体尺寸分布特征和覆岩应力大小构建相应的工程尺度模型，同时根据现场实际条件下出水口的位置及允许携带颗粒的大小进行模拟。在这种情况下就能模拟获得真实条件下不同水位放水过程中孔隙率的演化情况。同时可以根据真实放水速度计算出入水口水压的变化及覆盖范围，进而可以在模拟过程中评估水位高度和流速的变化，具体工程尺度的模拟平面截图如图10所示。

图10 工程尺度流固耦合模拟方案 Fig. 10 Flow-solid coupling model of caving zone under engineering-scale conditions

5 结 论

( 1 ) 针对矿井地下水库蓄放水的工程背景，构建了矿井水渗流的破碎岩体流固耦合模型，给出了 基于矿井水流速、垮落带孔隙率、破碎岩体半径等因素的破碎岩体所受流体压力的计算方程。量化分析了垮落带孔隙率、破碎岩体半径以及流体流速对破碎岩体所受流体压力的影响。

( 2 ) 流体压力主要由拖曳力和梯度力组成，但在矿井地下水库条件下，梯度力可以忽略不计。垮落带孔隙率的增加，促使流体压力急剧减小。考虑到采空区垮落带孔隙一般为0.3～0.6，在流体流速为0.01 m/s时无法携带垮落带破碎岩体，而当流体速度升高至1.925 m/s时，在孔隙率0.5时能携带半径1 m的破碎岩体。流体压力随着破碎岩体粒径的增加呈幂函数式增加，但破碎岩体的增加同时造成质量的升高，使得破碎岩体移动所需的流体压力大幅度增加，进而造成破碎岩体越小越容易被流体携带。

( 3 ) 基于本文构建的破碎岩体流固耦合模型，借助PFC3D与Python求解器进行了破碎岩体模型不同流速的数值模拟。由于破碎岩体间接触应力的存在，使得流体很难打破原有的平衡结构。只有游离于破碎岩体结构孔隙内的小颗粒岩体才能被流体携带，这对整体模型的孔隙率影响较小。只有在流体流速达到一定值时，破碎岩体结构被挤压，模型外部孔隙率大幅度降低，内部孔隙率则逐层出现递减，进而影响垮落带整体的渗透率分布情况。