不同工况下深部围岩分区破坏非连续变形试验研究
段昌瑞,郑 群,薛俊华,余国锋,罗 勇
( 1. 淮南矿业( 集团 )有限责任公司,安徽 淮南 232001;2. 煤炭开采国家工程技术研究院,安徽 淮南 232001;3. 深部煤炭开采与环境保护国家重点实验室,安徽 淮南 232001 )
淮南矿区是我国华东地区最大的矿区之一,目前矿井已开拓延伸至地下-900 m左右的深度,主力矿井开采深度均已超过1 000 m,矿区地质条件复杂,断层构造多,水平方向地应力大,软岩遇水会膨胀,深部岩层裂隙发育。在高地应力、高温、高水压力及较长的时间效应作用下,深部岩体的组织结构、基本行为特征和工程响应均发生根本性变 化[1-2],引发诸多与浅部完全不同的亟需解决的深部工程技术问题。伴随着深部岩体工程的响应发生了一系列新的特征科学现象,如分区破裂化现象、岩饼、岩爆、顶板冒落、片帮剥落、底板隆起、突水、软弱围岩大变形和流变现象等[3-6]。深部岩体的力学属性与浅部岩体相比具有强约束、宽时域、大变形和时间效应等特点,呈现复杂的非线性转化特 征[7]。如深部岩石可能从浅部的弹脆性属性转变成黏塑性属性,也可能由于高孔隙水压力的作用使得原本延性的岩石呈现脆性破坏或分区破裂化现象。深井巷道围岩应力作用极其复杂,通常为自重应力、构造应力和采动应力等多种应力因素的综合作用,而且水平方向应力高[8-11];此外,高地压围岩承受的应力水平高,不仅在工程施工过程中应力集中阶段围岩变形破坏十分突出,而且在应力基本恒定阶段围岩变形破坏仍然比较剧烈,常表现为分区破碎、松散、臌胀、大变形、大流变等特征[12-13]。李英杰和潘一山[14]等指出分区破裂化的发生与大采深有关,认为支撑压力区的劈裂破坏是岩石分区碎裂化现象产生的必要条件;钱七虎[15]等研究了深部岩体工程响应的特征,界定了“深部”岩体的范围,对深地下工程建设过程中围岩出现的交替破裂区和非破裂区的新破坏形态,将其称之为分区破裂化现象;李术才[16-19]等在淮南矿区通过钻孔电视直观观测了围岩内部分区破坏的形态和岩层分布,监测发现了分区破裂化现象,并得出了围岩分区破裂的半径与巷道半径的基本关系。
淮南矿区丁集煤矿二水平( -910 m )西二11-2采区南轨道大巷实测发现围岩内部形成破裂区和完整区间隔交替的分区破裂现象,如图1所示。深井巷道中的大变形和围岩稳定性等难题均与深地下工程所处的高地应力环境有关,巷道的开拓布局及开挖等直接影响着巷道围岩的受力变形,亟需展开高地应力作用下硐室围岩变形及支护对策的相关研究。
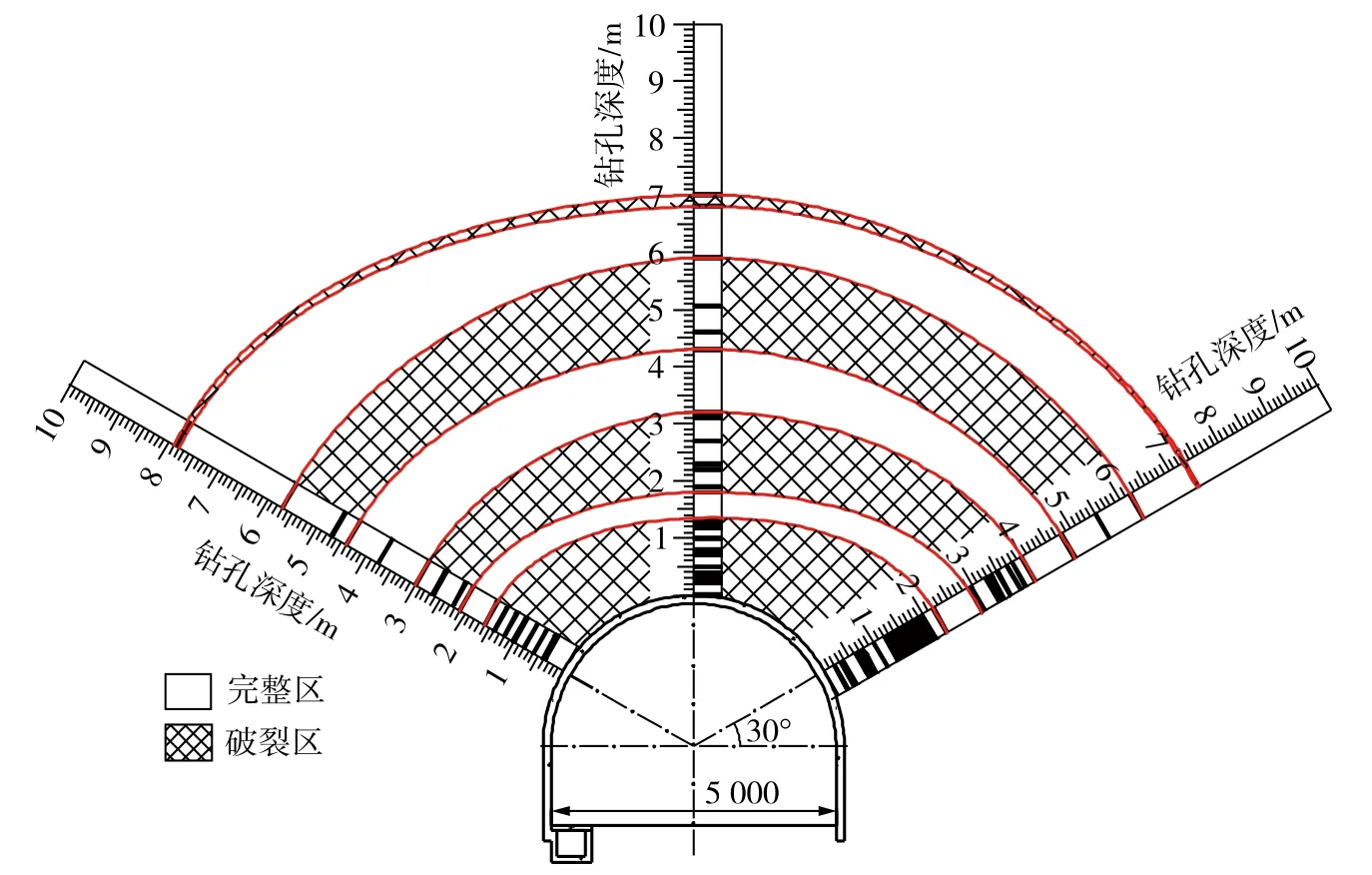
图1 丁集煤矿围岩分区破裂实测现象 Fig. 1 Zonal rupture of surrounding rock in Dingji Coal Mine
分区破裂化的理论研究和发生机理目前仍存在分歧,但可以肯定的是深部岩体变形破坏机理是决定其支护稳定性的前提。单纯依赖大量的现场实测寻求规律是不现实的,本文主要通过物理手段开展了4种不同工况下硐室的模型试验,详细模拟研究了淮南矿区丁集煤矿西二南轨道大巷工程的整体受力特性、变形趋势及稳定性特点,从而为巷道围岩稳定控制和支护对策提供理论指导。
1 模型试验
1.1 试验条件
试验原型为淮南矿区丁集煤矿-910 m西二11-2采区南轨道大巷,采用深部巷道工程围岩破裂机模拟试验装置进行模拟研究。试验条件:巷道开挖深度为1 005 m,岩体密度为2.4×103kg/m3,岩体垂直荷载Pv0为24.0 MPa,侧压系数为0.33,水平荷载Ph0为8.0 MPa。通过室内试验测得饱和单轴抗压强度Rc为40 MPa。地下工程常用的直墙拱顶形巷道宽度G为3 000 mm。直墙拱顶高度为1.5 m。图2为本次试验所采用的模拟试验系统。

图2 深部巷道围岩破坏机理模拟试验系统 Fig. 2 Model test system on the zonal disintegration in deep rock
试验对深部巷道在不同应力、不同加-卸载条件下围岩的受力特点和破坏机理进行了模拟研究,主要有以下4种工况,具体试验内容见表1,模型试验的不同加载和受力工况设计详述如下。
( 1 ) 不同开挖应力对比试验
M1模型体的开挖应力( 即开挖巷道时,模型体中心部位所受到的垂直荷载 )为Pv0=1.44 MPa=0.63Rc,侧压系数为N=1/3,巷道轴向保持平面应变条件;M2模型体的开挖应力为Pv0=4.94 MPa=2.17Rc,侧压系数为N=1/3,巷道轴向保持平面应变条件。试验简图如图3所示。
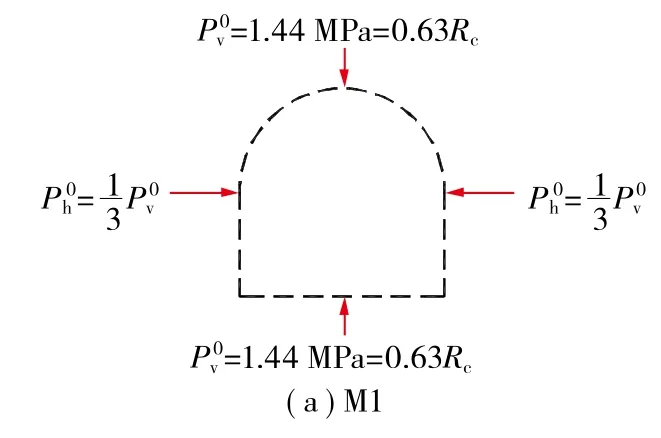
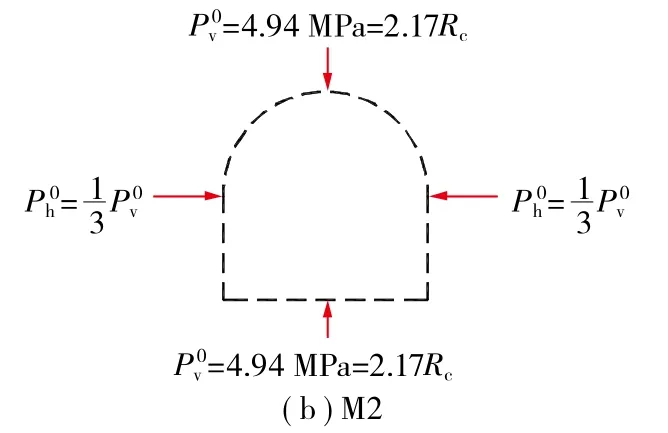
图3 M1,M2试验工况加载条件 Fig. 3 Load condition of difficult working
( 2 ) 最大荷载方向与巷道轴线成60°试验
M3试验条件:最大荷载方向与洞轴线成60°,根据淮南矿区岩石测压系数统计回归分析结果,侧压系数为N=1/3,巷道轴向保持平面应变条件,试验简图如图4所示。

图4 M3加载工况 Fig. 4 M3 working condition
( 3 ) 最大荷载方向与巷道轴线平行
M4为最大载荷作用方向平行于巷道轴向方向时的试验条件,加载工况如图5所示。
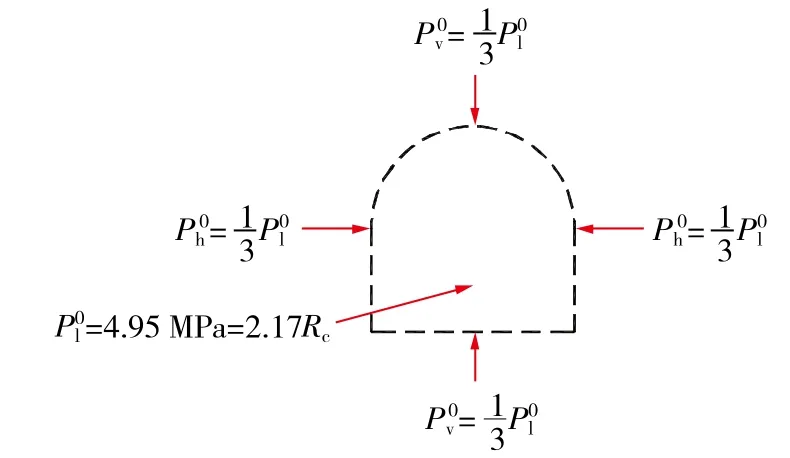
图5 M4试验条件 Fig. 5 M4 test condition
1.2 模型制作及测点布置
( 1 ) 模型制作
模型由上下分层拼接而成,每块尺寸100 cm×100 cm×20 cm( 长×宽×厚 )。在其中一块模型层表面贴好测试元件,将2块模型黏合为一个整体。整体模型吊装入装置内后,在模型表面设置四氟乙烯减摩措施。
( 2 ) 测点布置
为获得模型巷道周围介质在试验过程中的应变场,在中间层面( 下半部模型体上表面 )上布置3条应变测量线:第1条位于拱顶正上方,第2条位于底板正下方,第3条位于左侧墙中部水平正左方,在每一条测量线上布置11个测点,每一个测点上布置2个应变片,应变片规格为2 mm×5 mm的胶基应变片,其中一个测点测量巷道径向方向的应变,另一个测量巷道环向方向的应变。因此,在一个模型体内分别布置33个环向应变测点和33个径向应变测点。由于在拱顶正上方和底板正下方还布置有断裂丝测量线,因此,这两个部位的应变测量线布置在距模型体中线20 mm的地方,具体布置如图6所示。
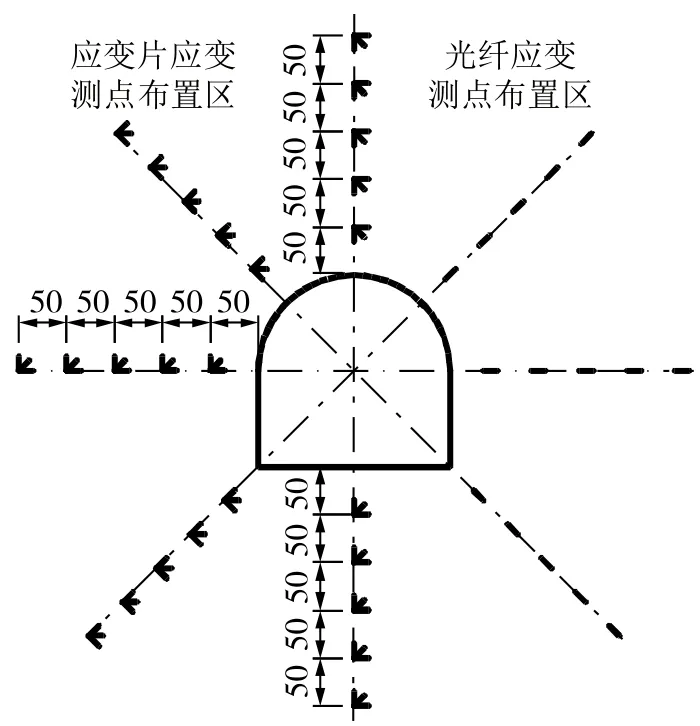
图6 应变测点布置 Fig. 6 Arrangement of measuring points
( 3 ) 断裂丝显示技术
采用断裂丝围岩裂隙跟踪技术,可直观获取模型体内是否有裂缝及其分布位置。在模型正拱顶上方、右侧墙中部水平正右方、底板正下方各布置1条断裂丝,每条断裂丝长度为100 mm,在每条断裂丝上设置21个触点,每2个触点之间的间距为5 mm, 每个触点通过2 mm×3 mm接线端子与引出线相连,每相邻2根引出线与LED指示灯相连。由于断裂 丝电阻要小于LED灯的电阻,当该段断裂丝没有断裂时,电流从该段断裂丝通过,LED灯不亮;当两 个触点之间的断裂丝断裂时,电流从对应的LED灯电路通过,LED灯亮,表明该段断裂丝断裂,即该处产生裂纹。断裂丝技术原理及布置方案如图7所示。
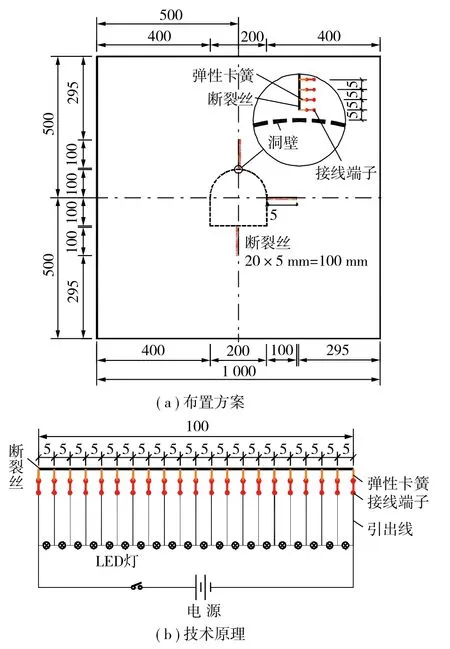
图7 断裂丝技术原理 Fig. 7 Technology schematic of broken wire
1.3 开挖与加载
荷载分步施加,每级荷载增量0.4 MPa,逐级加到开挖荷载,并保持其稳定进行巷道开挖。开挖时,先从中心位置向下钻出1个25 mm左右的圆形漏渣孔,然后用自制小型掘进工具先从轮廓线之内向下挖掘,使之与设计的形状尺寸基本一致。开挖过程中要始终保持压力荷载稳定。开挖过程中,要进行测量,开挖进尺为5 cm,每个开挖进尺均进行测量读数。
2 结果分析
模型试验完成后,沿垂直于硐室轴线的方向对模型体进行解剖,解剖面距模型体顶面的距离为15 cm,图8为硐室周边破裂剖面,图8( a )~( d )分别对应M1,M2,M3,M4模型体,其中M1,M2,M3为平面应变模型,M4为轴向力最大的三向加载模型。

图8 硐室周边破断剖面 Fig. 8 Displacement of surrounding rock
从裂纹演化分布情况看,4种工况下巷道两帮均发生破坏,值得注意的是M4模型的拱部和底部也出现了环状破坏。从断裂过程来看,M1,M2,M3,M4断裂顺序均为自邻近硐壁附近点开始向深部发展,说明巷道围岩的破坏是自硐壁向内部发展的。
试验对模型体的变形和裂缝进行了测量,从测量数据来看,M1模型左侧墙裂缝最宽处位于与拱脚平齐部位,分布宽度为自拱脚至向外90 mm,裂缝高度140 mm,裂隙体宽度3~20 mm。右侧墙裂缝最宽处位于与拱脚平齐部位,分布宽度为自拱脚向外90 mm,裂缝高度150 mm,裂隙体宽度3~20 mm。
M2模型巷道高度由200 mm减小至195 mm,高度减小了5 mm;巷道底板跨度由200 mm减小至150 mm,减小了50 mm;墙中部跨度由200 mm减小至170 mm,减小了30 mm;M2裂缝自墙脚产生后,随着距底板距离的增大,裂缝也一直向上发展,但当遇到自拱脚斜向上的裂缝时,停止发展。整体上,尽管M1和M2开挖应力和最大荷载不同,但其宏观破坏现象基本相同。
M3模型巷道高度由200 mm减小至193 mm,高度减小了7 mm;巷道底板跨度由200 mm减小至150 mm,减小了50 mm;墙中跨度由200 mm减小至180 mm,减小了20 mm,左、右侧墙裂缝分布宽度为70 mm。
M4模型体巷道高度由200 mm减小至190 mm,高度减小了10 mm;巷道外形没有产生变形,侧墙仍垂直于底板,墙中跨度由200 mm减少至185 mm,减少了15 mm,值得注意的是在围岩体内产生了围绕硐壁环状分区破裂。最先断裂破坏是底板,断裂深度最大,然后是侧墙部位,拱顶以上围岩最晚破坏,断裂深度最小,该结果与实测观察巷道破坏过程是一致的。
对上述4种工况下的直墙圆拱形巷道周边介质的应变测试结果进行整理后如图9~11所示。综合对比分析可知,由于M1,M2模型工况相似,仅作用力的大小不同,2者巷道变形特征类似,具体为拱顶环向应变均处于受压状态,侧墙径向应变均处于受拉状态;底板径向应变由受压状态转变为受拉状态,距底板最远处测点径向压应变值是距底板最近处测点径向压应变值的12.2~15倍。
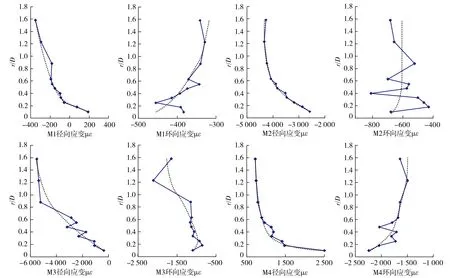
图9 M1,M2,M3,M4模型顶板径向应变和环向应变 Fig. 9 Radial strain and annular strain of difficult condition roof

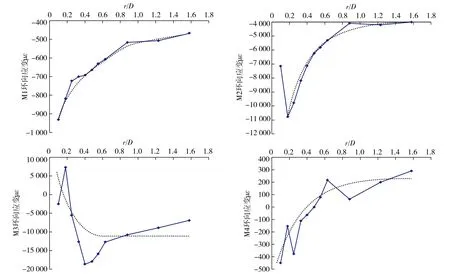
图10 M1,M2,M3,M4模型侧墙径向应变和环向应变曲线 Fig. 10 Radial strain and annular strain of roadway's sides on difficult condition

图11 M1,M2,M3,M4模型底板径向和环向应变曲线 Fig. 11 Radial strain and annular strain of difficult condition floor
M3拱顶上方模型体内的径向应变和环向应变处于受压状态,中部模型体径向应变在( 硐壁距离/巷道跨度比值 )r/D=1.0范围内为拉应变,墙中部位模型体环向应变在r/D=0.2范围内为压应变。底板下部模型体内径向应变在r/D=0.4范围内为拉应变,且在r/D=0.9时,径向应变值开始进行塑性调整,环向应变均处于受压状态,在r/D=0.6时,应变值开始进行塑性调整。
M4拱顶上方模型体内径向应变基本上均处于受拉状态,在硐壁附近拉应变值最大。拱顶上方环向应变均处于受压状态,在硐壁附近应变值最大。墙中部位径向应变受拉,在硐壁附近拉应变值最大。在自硐壁至距硐壁95 mm内环向应变处于受压状态,压应变值随距硐壁距离的增大而逐渐减小;较远处环向应变处于受拉状态,拉应变值随着距硐壁距离的增大而逐渐增大,巷道开挖完毕后,底板下部模型体内径向应变也处于受拉状态。可见M4条件下,模型体周边的径向应变均为拉应变,这便是形成分区破裂的主要原因。
3 讨论分析
如前所述,对于分区破裂化的发生机理尚有争议,通过现场实测,室内模型试验得到当最大载荷作用方向与巷道轴向方向平行时,巷道周边会产生环形、分区破裂化形态。对本试验分区破裂现象产生的条件作如下分析总结:模型硐室( 巷道 )开挖后,周边应力重新调整,产生应力集中,随之发生剪切破坏,形成剪切破坏区,峰值逐渐向围岩深部转移,期间产生“剪切破裂波”的传播。当有较大轴压和开挖应力时,围岩逐渐发生拉伸破坏,但拉伸破坏速度远大于剪切破坏速度,并在剪切破裂波之前完成;破坏后的围岩得以卸压,剪切随之停止,即为未破坏区( 完整区 )。已发生拉伸破坏的区域类似于新的更大的开挖面,载荷重复作用下,破坏逐渐向内部发展,直至某一时刻开挖面的径向拉应变不再超过围岩的极限抗拉应变时即停止。岩体的这种不连续且交替出现的环状裂隙区便形成了分区破裂化现象。
4 结 论
( 1 ) 模型拱顶、侧墙和底板周边径向应变均呈现拉应变,形成环状裂缝;在较大轴压作用下,巷道周边产生剪切破坏和拉伸破坏,但拉伸、剪切破坏区形成速度不一致,拉伸破坏的速度远大于剪切破裂的速度,使周边产生分区破坏。
( 2 ) 直墙圆拱巷道发生分区破裂的特点:在帮部呈现分层断裂,在拱顶和底部呈现滑移型断裂。当最大荷载垂直于巷道轴线,在侧压系数为1/3条件下,直墙拱顶巷道破坏由墙脚和拱脚开始,向边墙部位发展,最后在边墙部位发生破坏。
( 3 ) 深部开采时,采深大且地应力场复杂,最大地应力方向往往又沿水平方向发展,硐室围岩有可能在较大的轴向压应力作用下发生分层断裂现象,为避免破坏向硐壁深部转移,需对围岩进行及时加固,支护长度及支护密度需根据监测结果和不同受力工况进行判识和调整。

