基于改进多元统计控制图的接触网状态综合评价方法

程宏波，王佳鑫，刘杰，曹雨璠，李宏逸，徐学平

(1. 华东交通大学电气与自动化工程学院，江西南昌 330013；2. 中国铁路武汉局集团有限公司宜昌综合维修段，湖北宜昌 443000)

接触网是电气化铁路的关键设备。由于本身不携带能源，电力机车运行所需的能源都由沿线架设的接触网提供，因此，保证接触网处于良好的工作状态是实现电气化铁路安全正点运行的基础。准确的状态评价是了解接触网真实运行状态、掌握接触网发展变化趋势、指导接触网运营检修的前提。目前，接触网的检测方法和检测手段较多，各种接触式和非接触式检测设备较为成熟，接触网的各类静态和动态参数获取较为全面。其中，接触网几何参数的接触式测量历史较久、使用最为普遍[1],常用的接触网检测车都可以获取接触网的拉出值、导高等几何参数[2]，并可在此基础上得到反映接触网平顺性的高差、坡度等参数[3]。而随着检测技术的进步，接触网动态参数如弓网接触力、离线性能[4]等参数也逐渐普及，激光等各类非接触式测量也开始用于接触线磨耗的测量[5]，而当前建设的高铁供电安全检测监测系统(6C 系统)，则能实现对接触网全方位、全覆盖的综合监测。与日渐发展的检测手段相比，接触网状态的评价方法则显得相对较为简单。目前普遍采用的是对接触网各单项检测参数进行阈值比较的方法，通过各项指标分别与事先设定的标准值进行比较，以发现接触网的局部缺陷[6]。这种方法阈值的设定缺乏足够的理论支持，且没有考虑接触网不同检测参数之间的相互关联和相互影响，有时会得到互相冲突的评价结果。而且阈值比较方法只能得到“正常”和“超标”2 种结论，评价结果比较简单，无法反映接触网状态发展变化的规律，也不能体现接触网健康状态发展变化的趋势。接触网的检测参数从不同的侧面反映了同段接触网的工作状态，因此，考虑检测参数相互之间的影响，利用检测参数对接触网的工作状态进行综合评价，所得的结果将更加准确、更加全面。王志良等[7]根据接触网各指标的特点和权重，给出了接触网质量综合评价指标的计算方法，确定了权重参数的取值，并提出了分级评判标准。张志勇[8]通过层次分析法建立综合评价系数，对接触网的运行状态和质量状况进行评价。王洪德等[9]采用云模型研究高铁接触网系统安全性评价问题，利用结构熵权法对高铁接触网评价指标权重做出主观评价。这几种方法在确定参数的权重时，都需要人为指定不同指标的权重系数，主观性强。张文轩等[10]综合考虑影响接触网静态质量与弓网运行质量的多个参数，对整区段接触网的质量进行评价，用以指导接触网维修策略的制定和维修资源的分配，但整区段的综合评价缺乏对现场维修工作的指导。为克服评价过程中主观性的影响，刘仕兵等[11-12]利用熵权理论挖掘检测数据中所蕴含的信息,采用熵权法确定各检测指标的评价权重,实现对接触网健康状态的综合评估，但接触网参数合理隶属度函数的确定比较困难。控制图是用于分析和判断生产过程是否处于稳定状态所使用的一种带有控制界限的图[13-14]，是质量控制管理的一种重要手段和工具[15]。在正常状态下，接触网的状态参数将围绕着特定的值在一定范围内波动。接触网运营管理的目的就是实现接触网的质量控制，努力使接触网的参数保持在正常的范围内。因此，通过对接触网检测参数的测定、记录和评估，通过构造接触网多元检测参数的统计控制图，可实现对接触网异常运行状态的判断。但常用的控制图只有“正常”和“异常”2 种状态，二元的判断结果无法体现接触网状态发展变化的规律和趋势，无法对接触网的预防性维修提供支撑。因此，在多元统计控制分析的基础上，依据可靠度对接触网的状态进行细分，将多元统计控制图的状态拓展为多个，从而实现接触网多维状态参数的统一综合评价，可为接触网的健康管理提供有效手段，为接触网的运营维护提供具体指导。

1 接触网的评价参数与状态分布

1.1 接触网的评价参数

接触网是由众多零部件组成的一个复杂整体，它通过整体的机械结构向电力机车的受电弓提供满足要求的电能。因此，反映接触网状态的指标参数有很多，既有反映其机械结构的几何参数，也有反映其供流效果的电气参数。

在众多的接触网参数中，选取最具代表性的接触网参数X=(X导高,X拉出值,X接触力,X高差,X硬点)作为评价指标，建立相应的接触网状态评价向量。其中，拉出值、导高是接触网最基础的几何参数，影响着受电弓和接触线之间的工作状态，超标的拉出值和导高可能导致弓网故障，造成大的弓网事故，因此，拉出值和导高属于接触网的安全性指标。而硬点和高差则反映了接触网的平顺性。弓网接触力和离线时间反映了接触网和受电弓之间配合的好坏，属于受流性能指标。这几个典型指标分别从不同的方面反映了接触网的状态，具有较好的代表性，而且，其检测数据较易获取。

1.2 接触网的状态分布

作为由众多零部件组成的复杂系统，接触网的状态会随着运行时间的积累而逐步退化。接触网系统的可靠性随运行时间的变化关系如图1所示。

从图1可以看到，随着运行时间的积累，接触网的可靠性逐步降低，运行状态逐步变化，经历由好到差的变化过程。当接触网的运行可靠性高时，接触网设备的故障几率低，停电时间少，此时接触网处于较优的状态；而随着时间的积累，接触网的可靠性逐步降低，设备性能逐步退化，接触网故障几率增加，最终会退化到比较差的状态。为更精确的反映接触网状态发展变化的规律，结合接触网可靠性变化规律，将接触网状态划分为“优”、“良”、“中”、“差”4 个状态，其含义如表1所示。

图1 接触网可靠度与状态之间关系Fig.1 Relationship between reliability and state of catenary

表1 接触网状态的划分及其含义Table 1 Classification and meaning of catenary status

接触网的整个寿命周期就是在这些不同状态之间的演变，对于接触网系统来说，接触网不同状态在整个生命周期的分布具有统计规律。作为一个典型的机械系统，接触网系统的可靠性变化满足威布尔分布，其可靠度可表示为[16]：

其中：T为接触网的整个生命周期时长。因此，根据检测参数评价出的接触网状态应满足上述统计规律的分布。

2 接触网状态参数的多元统计评价方法

处于良好状态意味着接触网的参数在设计所期望的范围附近波动，因此，可以通过绘制接触网状态参数的统计图，根据参数是否处于正常的波动范围来判断接触网的状态。

考虑测量误差及干扰的影响，正常接触网参数的测量值应满足正态分布，即X～N(μ,σ2)，其概率密度函数为：

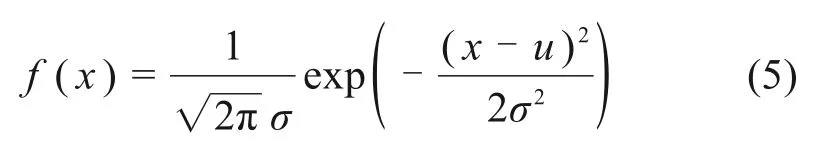
其中：μ为接触网参数的期望值，是正态分布的位置参数；σ2为接触网参数的方差。

根据概率密度函数的定义可得：

即接触网状态参数在均值附近波动，且落于某个区间的概率等于其处于该区间状态的概率，据此，接触网状态参数统计分析的原理如图2所示。

图2 接触网状态参数统计分析的原理Fig.2 Principle of statistical analysis of catenary status parameters

接触网参数数值的分布满足概率密度函数确定的统计规律，在正常情况下，接触网检测参数的值围绕着均值上下在一定的范围内波动；当由于某些原因导致接触网的检测参数异常时，它将超出这个范围，体现在控制图上为超出控制限，因此，可以采用统计控制图对接触网的状态进行判断。

由于接触网的检测参数众多且相互之间互相关联、相互影响，若对每一项参数单独进行一元控制图判断的话，工作量大，且不能体现参数相互之间的关联影响，容易做出错误判断。多元统计控制图可以将多维状态参数转换为一个统计量进行综合判断，效率高且更准确。

2.1 多元T2控制图

当接触网多维参数的均值向量μ和协方差矩阵Σ 同时稳定时，接触网才处于正常状态，因此，多元控制图不仅能反映接触网参数均值的变化，还能反映接触网参数之间关联关系的变化情况。

检测变量的整体均值和协方差未知时，可利用有限样本数据的均值Xˉ和协方差S对整体均值μ和协方差Σ 进行估计。定义第i个样本的T2统计量为[17]：

其中：n表示测量值的个数，Ti

2表示第i个统计量，Xi表示第i个测量值的状态向量，-X表示测量值的均值，S表示不同指标之间的协方差向量。

其中：p为状态参数的维数。

由于接触网参数落于不同区间的置信度与其状态概率相关，因而根据式(4)所得的状态概率可得不同状态的置信度，进而由式(8)求得T2控制图中不同状态的控制限。针对每个检测样本，计算其T2统计量并与其控制限相比较，根据比较结果可判断出接触网参数所落的范围，进而对接触网状态做出判断。

2.2 多元指数加权移动平均控制图

多元指数加权移动平均(multivariate exponentially weighted moving average，MEWMA) 控制图引入相邻样本点的值，利用多个样本值的联合信息形成累积效应，从而可以更早的发现状态波动迹象。

对第i个样本数据进行移动加权平均可得[18]：

2.3 多元累积和控制图

多元累积和(multivariate cumulative sum，MCUSUM)控制图通过计算样本值与目标值差值的累积和来判断状态是否正常，可以解决小偏移的判断问题。

第i个样本的向量累积和为[19]：

其中，K=n(Xi-Xˉ)S-1(Xi-Xˉ)′/2 为过程偏移检测系数，从式(9)可以看到，如果要在多变量情况下能够检出变量的累计和，K必须与Si-1+(Xi-Xˉ) 方向相同。由于MCUSUM 的初值一般取E(X) =μ0，因而S0= 0。

MCUSUM控制图的打点值取：

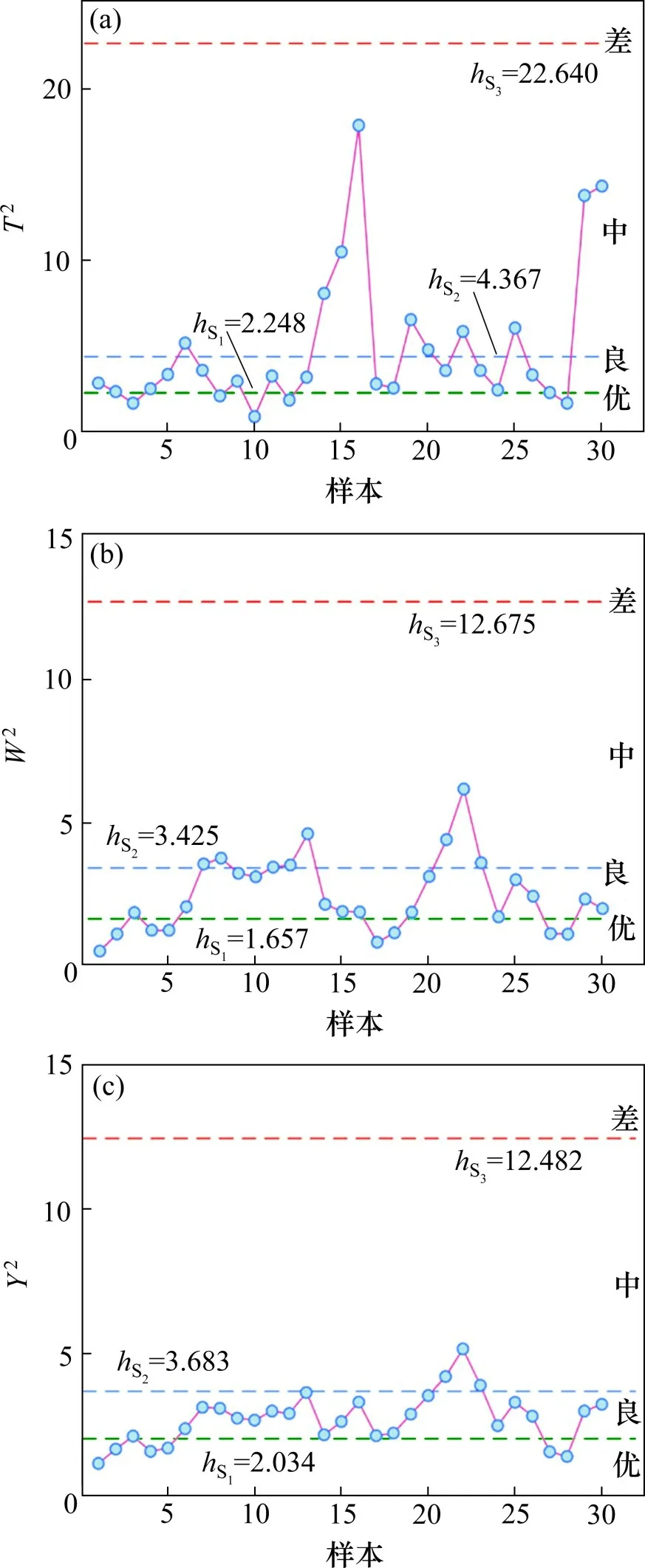
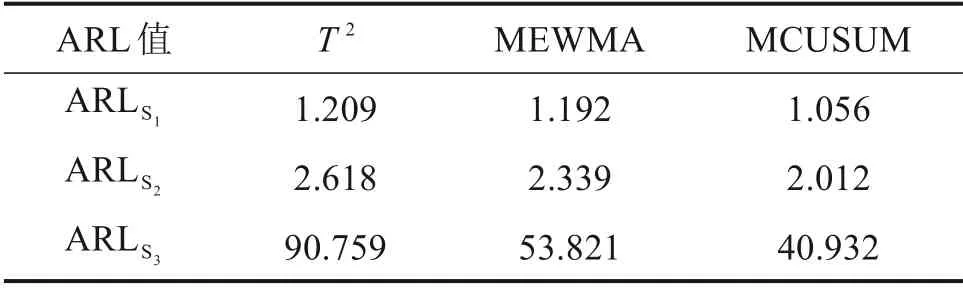
同样，控制限h与置信度和期望的检测灵敏度有关，当Y2i

3 实例分析

取某线路接触网检测参数为例，选取其中某一区段共30 km 的检测数据进行分析，该段接触网的各参数检测数据如表2所示。

表2 某段接触网的状态检测参数Table 2 State detection parameters of a certain segment of the catenary

接触网系统的可靠性函数由文献[20]的故障数据拟合得到，根据该可靠性函数，得到接触网各状态的分布情况如表3所示。

根据式(7)，式(12)和式(14)方法对该段接触网的检测数据进行处理，计算其在各多元统计控制图中的打点值。根据表3中的置信度，分别计算不同控制图中不同状态的控制限如表4所示。

表3 接触网的状态分布情况Table 3 Status distribution of catenary

表4 3种控制图不同状态控制限Table 4 Different state control limits of three control charts

将计算的接触网参数多元统计值与各状态的控制限绘制于控制图上，得到该段接触网检测参数的3种多元统计控制图如图3所示。

从图3 中可以看到，3 种控制图都可以将接触网的多维状态参数转化为一维的统计量，并以图形化的形式直观展示。针对该段接触网，其状态参数的统计量都在最高限值的范围以内，没有点落在“差”的范围内。3 种控制图对该段接触网状态评价的结果基本一致，但与MEWMA 控制图及MCUSUM 控制图相比，多元T2控制图的评价结果准确且更严格。

图3 3种状态评价图Fig.3 Three state evaluation diagrams

平均运行链长(Average Run Length，ARL)是评价控制图优劣的一个常用指标，利用Monte Carlo 仿真法求解得到3 个控制图的ARL 值如表5所示。

表5 3种控制图不同状态限下的ARL大小Table 5 ARL size under different state limits of three control charts

从表5 中可以看到，针对不同的状态控制限，多元T2控制图的ARL值总是最大的，而MCUSUM控制图的ARL 值总是最小的，反映出3 种控制图中多元T2控制图在过程受控时误报的可能最小，而MCUSUM 控制图则对过程变化最敏感。由于该段接触网的状态分布没有落在“差”这一状态内的点，反映出接触网处于受控状态，因而，3 种控制图中ARL 值最大的多元T2控制图更适宜用于接触网的状态评价。

以选定的多元T2控制图为工具，分析该接触网另外25 km 检测数据如图4 所示。为便于对照，该段接触网各参数的变化曲线绘制于图5中，图中黑色实线是根据现行《高速铁路接触网运行维修规则》所确定的该参数的最大允许值。

图4 某段接触网参数的多元T2评价图Fig.4 Multivariate T2 evaluation diagram of a certain section of catenary parameters

图5 该段接触网参数的变化情况Fig.5 Changes of catenary parameters in this segment

从图4可以看到，利用多元T2控制图，无需逐一进行比较，即可将该段接触网不同位置处的状态直观的判断出来。而且，在综合了接触网各个检测参数的多元信息之后，多元T2控制图可以更加清晰直观的显示出接触网综合状态发展变化的趋势，如从多元T2控制图可以很明显的看到从第6点开始接触网的状态在逐步的变差，且在第10 点位置处已快接近“差”的状态控制限，因此，可在后期日常维护时加强对第6 至第10 点处接触网的检修，实现预防性维修，以避免故障的发生。

另外，由于多元统计量综合了各个检测参数的信息，且协方差考虑了各参数相互之间关联关系的影响，因此，多元T2控制图对接触网状态参数的变化要比现行单参数比较的方法更加灵敏，如图中的第4，14，20和24点，在图5的单参数变化中，这些点都只有某一个或某2个参数发生了并不显著的变化，但由于参数之间的关联关系发生了变化，因此，在多元T2控制图中显示的较为明显。

4 结论

1) 多元统计控制方法可将接触网的多维状态参数转化为一个统计量进行判断，既可以反映接触网状态参数的变化，也能够反映接触网状态参数关联关系的变化，可用来对接触网的多维状态参数进行处理。

2) 接触网的状态与可靠度紧密相连，根据接触网系统的可靠度将接触网的状态进行细分，并由此得到接触网不同状态在多元统计控制图中对应的控制限，可用来对细分的接触网状态进行评价。

3) 利用多元统计控制图可以将接触网的多维状态参数变化以图形化的形式显示出来，并实现接触网状态的直观判断，同时可清晰直观的显示出接触网状态变化的趋势。

4) 多元统计控制图相较于现行的单参数阈值比较方法更简单、更直观，且对接触网参数的波动更灵敏。