基于对数稀布阵的FDA-MIMO干扰抑制

王 博，陈楚舒，马学亮，朱鹏羽

(1.95972部队, 甘肃酒泉, 735300; 2.空军工程大学防空反导学院, 西安, 710051)

FDA雷达通过改变载波频率和频偏增量以离散方式扫描空间中的每个点，因此提供了极大的电子反对抗应用潜力[1-4]。相控阵与距离无关的波束指向特性使其在抑制支援式干扰的过程中会出现主瓣分裂的问题。文献[5]结合可能的目标区域先验知识，提出了一种基于FDA-MIMO雷达协方差矩阵重构的鲁棒性欺骗干扰抑制方法，显著提高了欺骗干扰抑制性能。文献[6]提出了一种基于FDA-MIMO发射非正交波形的距离欺骗干扰抑制方法。文献[7]建立了以FDA为发射阵列的空时自适应处理雷达新框架，使得距离模糊的杂波在空间频域中可以被有效抑制。文献[8]提出了一种基于FDA抑制高超音速飞行器前视雷达杂波的新方法。现有文献中较少有基于FDA-MIMO结构通过自适应波束形成算法抑制随队式干扰的研究[9-11]。本文在FDA雷达方向图距离-角度解耦技术的基础上，首先使用对数稀布阵代替基本的一维均匀线性阵列结构，再通过仿真验证了采用自适应波束形成算法的FDA-MIMO结构能够有效抑制支援式干扰。

1 FDA-MIMO结构模型

图1所示为均匀线性FDA(uniform linear array frequency diverse array，ULFDA)阵列：

图1 ULFDA基本结构

设载波频率为f0，相邻阵元间的频偏增量为Δf，则第n个阵元辐射信号的频率为：

fn=f0+nΔf,n=0,1,…,N-1

(1)

窄带条件下，t时刻阵元n的发射信号为：

sn(t)=exp(j2πfnt),n=0,1,…,N-1

(2)

阵元n发射的信号到达远场点观测点(R,θ)的信号表达式为：

(3)

式中：Rn=R-ndsinθ，R为参考阵元到目标点的距离，d为阵元间距，c为光速。

采用如图1所示的阵列作为收发共型阵，信号在发射端经赋相或加权后向空间辐射，经目标二次反射回接收阵列，在接收端通过采用不同的滤波方式可以构成相应的发射-接收机结构，并最终得到接收端的方向图[12]。文献[13]中对带限相干处理、全波段相干处理、全波段伪相干处理这3种FDA阵列接收端信号处理机制与FDA-PA、FDA-BFF、FDA-MIMO 3种接收机结构的对应关系做了详细的分析。

对式(3)中的发射信号加权使其到达远场目标(R0,θ0)：

srn(t)=

(4)

经目标二次反射后被接收阵列阵元m接收的信号形式为：

rm(t;θ0,R0)=

(5)

在每一个接收通道中通过N个窄带滤波器对接收阵列阵元m接收到的所有信号进行分离，对分离后的回波数据按接收通道进行重排，得到数据大小为N×N的信号，对重排后的信号进行普通波束扫描，可得FDA-MIMO结构：

(6)

2 基于对数稀布阵的干扰抑制

基本ULFDA结构其发射方向图中存在着距离-角度的耦合问题，这就给基于稳健波束形成方法的主瓣干扰抑制带来了模糊的问题。本节将对数稀布阵这一典型的不等间距阵列结构引入FDA-MIMO体制，结合方向图距离-角度解耦技术研究了当导向矢量存在偏差时，采用RCB算法对主瓣干扰的抑制效果。

2.1 对数稀布阵列

不等间距阵列是以单元间距为参变量的“距离分布阵”，图1中阵元n到参考阵元的距离为dn=nd,n=1,2,…,N-1，本文将这一线性取值方式改为dn=log (n+1)d,n=1,2,…,N-1从而得到如图2所示阵元间距分布呈对数变化的对数稀布阵：

图2 对数稀布阵列结构

2.2 方向图距离-角度解耦技术

相控阵(phased array,PA)相邻阵元间的相位差函数仅与波程差的变化有关，因而推导得到的相控阵方向图函数仅仅是角度的函数。与PA不同，FDA通过在相邻阵元间引入一个与阵列载频相比十分微小的频差，得到与波程差和传播距离相关的相位差函数，最终得到具有时间-距离-角度三维相关性的阵列方向图。

针对如何改进FDA“S型”波束图带来的多极值问题，主要有两种思路：一种着眼于频控函数设计，另一种主要着眼于阵列结构设计。文献[14]对比分析了对数、三角函数、指数函数及倒数4种非线性频控函数应用于一维均匀线性FDA的性能，得到正弦频控函数性能最优的结论。因此，本文在通过采用密度锥削阵重构一维线阵的基础上，引入正弦频控函数以实现FDA方向图的距离-角度解耦。

2.3 基于RCB的导向矢量修正

最小方差无失真响应(minimum variance distortionless response,MVDR)波束形成器用公式可表述为：

s.t.wHa(θs)=1,wHa(θi)=0

(7)

式中：R表示接收信号的协方差矩阵；wH表示接收端加权矢量；n(t)表示接收机噪声矢量。目标位于空间(Rs,θs)处，另有Q个干扰源分别位于(Ri,θi),i=1,2,…,Q。a(θs)表示目标信号的接收导向矢量，a(θi)表示干扰信号的接收导向矢量。

MVDR波束形成器的输出信干噪比(signal noise ratio,SINR)为：

(8)

实际中干扰源的位置估计会存在一定误差，从而导致通过求解式(7)得到的式(9)中最优加权矢量也存在误差：

(9)

本文在重构阵列结构的基础上，利用RCB(robust capon beamforming,RCB)算法对失配情况下的导向矢量进行优化[15]：

(10)

(11)

接收信号数据协方差矩阵可分解为：

(12)

结合式(11)、(12)，根据矩阵求逆引理可得：

(13)

根据谱分解的相关理论，RJ可分解为：

(14)

(15)

(16)

(17)

(18)

代入式(12)，得λ：

(19)

由此，能够得到修正后的目标导向矢量估计值：

(20)

3 仿真验证

考虑一个10阵元的一维线性阵列结构，阵元间距d=c/(2f0)，f0=10 GHz，Δf=10 kHz，t0=0 s，仿真验证本文分析的有效性。

3.1 对数稀布FDA与PA和ULFDA的发射方向对比

假设目标位于(30°,50 km)，由图3～5可知，PA的发射方向图主波束指向仅仅与角度相关，与距离无关，在抑制距离相关性干扰的过程中可能存在性能上的不足。FDA-MIMO的发射方向图呈现出距离-角度二维相关性，但其中同时存在多极值的问题。采用正弦频控函数的对数稀布FDA的发射方向图可在目标位置处形成点状的波束指向，有效消除了FDA-MIMO方向图中的距离-角度耦合。

图3 PA发射方向图

图4 FDA-MIMO发射方向图

图5 对数稀布FDA发射方向图

3.2 3种阵列的特性分析

3.2.1 干扰与目标位置在距离维、角度维同时可分时

假设目标位于(30°,50 km)，干扰位于(40°,55 km)，仿真对比基于MVDR的PA、基于MVDR的FDA-MIMO和基于RCB算法的对数稀布FDA 3种结构的干扰抑制性能，由图6～8可知，当干扰与目标的位置在空间中距离较远时，3种结构得到的阵列方向图都能在目标位置处保持有效增益的同时在干扰位置处实现置零。但PA的阵列方向图中的波束指向在距离维无分辨能力，FDA-MIMO的阵列方向图中存在多极值的问题。

图6 基于MVDR的PA阵列方向图

图7 基于MVDR的FDA-MIMO阵列方向图

图8 基于RCB算法的对数稀布FDA阵列方向图

3.2.2 干扰与目标位置在距离维可分、角度维接近时可分时

假设目标位于(30°,50 km)，干扰位于(33°,55 km)，仿真对比基于MVDR的PA、基于MVDR的FDA-MIMO和基于RCB算法的对数稀布FDA 3种结构的干扰抑制性能。由图9～11可知，当干扰与目标的位置在距离维可分同时在角度维接近时，PA的阵列方向图会出现主瓣畸变、旁瓣升高的问题。与图10相比，图11中对数稀布FDA的阵列方向图在实现干扰位置置零、主波束增益保持的同时，还有效消除了FDA-MIMO的阵列方向图中的多极值问题。

图9 基于MVDR的PA阵列方向图

图10 基于MVDR的FDA-MIMO阵列方向图

3.2.3 存在2个干扰，且干扰与目标位置在距离维可分、角度维接近时可分时

假设目标位于(30°,50 km)，干扰1位于(33°,55 km)，干扰2位于(27°,55 km)，仿真对比基于MVDR的PA、基于MVDR的FDA-MIMO和基于RCB算法的对数稀布FDA 3种结构的干扰抑制性能。由图12～14可知，当存在两个干扰与目标的位置在距离维可分同时在角度维接近时，PA的阵列方向图仍然出现了主瓣畸变、且无法有效区分干扰2与目标。图13和图14都可以实现对目标方向增益的保持和干扰方向的有效置零，但图14同时消除了方向图的多极值问题。

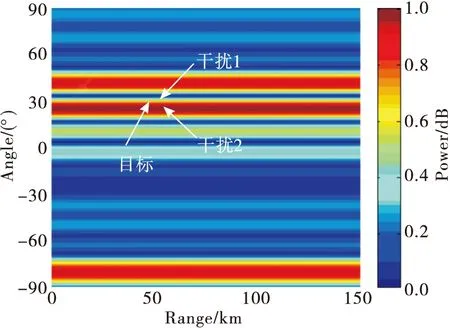
图12 基于MVDR的PA阵列方向图

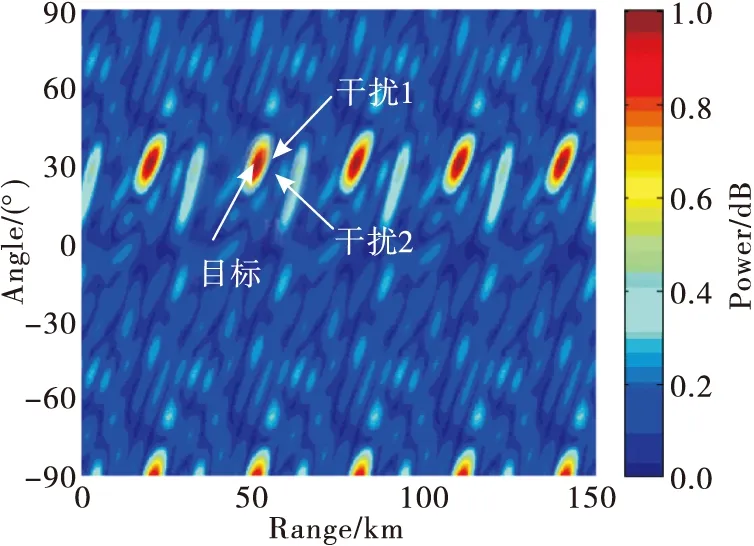
图13 基于MVDR的FDA-MIMO阵列方向图

图14 基于RCB算法的对数稀布FDA阵列方向图

3.3 存在2°指向误差时的主瓣纠偏

目标与干扰的位置与同时考虑导向矢量存在2°的指向误差，仿真对比基于MVDR的FDA-MIMO和基于RCB算法的对数稀布FDA两种结构的干扰抑制性能。当存在指向误差时，MVDR波束形成器收敛到存在误差的估计导向矢量上，图15中FDA-MIMO的主波束指向产生了明显偏移。如图16所示，基于RCB的对数稀布FDA阵列方向图仍可在目标位置处形成单一主瓣峰值，由于导向矢量的修正未出现波束指向的偏移，这同时也为后续关于目标参数估计的一系列分析中的模糊消除奠定了重要基础。由图可知本文算法性能优于FDA-MIMO及PA结构。

图15 基于MVDR的FDA-MIMO阵列方向图

图16 基于RCB算法的对数稀布FDA阵列方向图

4 结语

FDA雷达能够形成距离-角度-时间相关波束，在雷达目标的距离-方位角联合估计、射频隐身以及前视探测与成像等领域都有广阔的应用前景。当干扰与目标位置接近时，针对基于MVDR的PA、FDA-MIMO结构阵列方向图存在的性能不足，本文将一维均匀线性阵列结构改为对数稀布阵，同时引入正弦频控函数和RCB算法修正导向矢量，从而得到了方向图距离-角度解耦且能有效抑制支援式干扰的方法。

下一步将在此基础上，结合非时变FDA波束控制领域的最新研究成果，进一步开展FDA在电子战中的应用研究。