一种低交叉调整率的多路输出正激变换器设计方法
程红丽,田富涛,李 勇,
(1.西安科技大学 通信与信息工程学院,西安 710054;2.西安恒为电气科技有限公司 ,西安 710100)
电子技术的飞速发展,促使开关电源向高频化、小型化、多路输出方向发展[1-3]。由于正激变换器电路具有结构简单,可靠性高等优点[4-6],被广泛应用于低压大电流多路输出的场合[7],但多路输出正激变换器存在交叉调整率问题[8-9],例如,三路输出正激变换器,一路给大功率器件供电,其余两路给数字电路供电,原边开关管的驱动脉冲占空比主要由大功率输出路决定,这会导致原边开关管占空比变化范围较大,当功率路需求功率变化时,驱动脉冲占空比也会跟随发生变化,直接影响数字电路供电不稳,从而导致芯片不能正常工作。造成多路输出正激变换器交叉调整率问题的主要原因是副边输出功率不能合理控制以及输出整流二极管的压降不恒定[10]。大多数改善多路输出开关电源交叉调整率的控制策略需要分主辅路[11-13],主输出路采用闭环反馈控制,辅路开环或权值低的闭环,当主输出路负载发生变化时,主路需求功率发生变化,闭环反馈使得原边输入功率变化,变压器输出到辅路的功率变化,但辅路需求功率不变,使得辅路输出电压偏离期望电压,辅路交叉调整率变大,电压精度变低[14]。
目前,改善多路输出正激变换器交叉调整率的方法主要有:优化变压器[15]、加权反馈控制[16]、主辅路同步控制[17]等,这几种控制策略都能够在一定程度上改善交叉调整率;文献[15]中提到的优化变压器方法,通过减少变压器漏感来改善交叉调整率,但是改善效果有限;文献[16]利用加权反馈控制将整体的交叉调整率重新分配,使得各输出路交叉调整率得到一定的改善,但不能有效改善系统整体的交叉调整率;文献[17]提出了一种主辅路同步控制法,系统根据各路输出功率的大小判定主辅路,主路输出采用PID[18]控制调节,而辅路输出采用电压闭环控制,由于辅路控制精度不高,导致交叉调整率不能进一步改善。而功率分配控制策略[19]能从根本上改善多路输出反激变换器的交叉调整率问题,但反激变换器与正激变换器原理不同,功率分配控制策略不能直接应用到多路输出正激变换器拓扑[20-21]。为了从根本上改善多路输出正激变换器的交叉调整率问题,文中提出了一种适用于多路输出正激变换器的目标平均电流控制策略。并用该控制策略完成了某一军品电源的设计,具体设计指标为:1)输入电压范围:48~72 V;2)输出24 V/2 A、12 V/2 A和5 V/1A;3)交叉调整率小于2%;4)输出电压精度小于2%;5)负载调整率小于1.5%;6)电压调整率小于1.5%。
1 电路组成及控制策略
1.1 电路组成
目标平均电流控制的三路输出正激变换器的电路原理,如图1所示,在各输出路的整流二极管和绕组之间串入了开关管来控制输出电流,避免正激变换器工作在断续模式时,储能电感电流降为零,输出电压等于储能电感输入电压。
图1中VS为输入直流电压,VOi(i=1,2,3)为输出电压,IOi(i=1,2,3) 为输出电流,S1为原边开关管。SWi(i=1,2,3)为副边开关管,Dfi(i=1,2,3)为续流二极管,Dri(i=1,2,3)为整流二极管,Voni(i=1,2,3)为续流二极管Dfi阴极节点电压,Li(i=1,2,3)为三路输出的储能电感,Ci(i=1,2,3)为三路输出滤波电容,RLi(i=1,2,3)为三路输出所接输出路负载,W5为变压器T1的磁复位绕组。

图1 目标平均电流控制的多路输出正激变换器原理图Fig. 1 Schematic diagram of multiple output forward converter controlled by target average current
1.2 目标平均电流控制的原理
为了便于目标平均电流控制,多路输出正激变换器工作在断续模式。当输入为直流电压VS时,原边开关管S1和各输出路整流管SWi同时导通,原边输入电流Ip和副边储能电感电流ILi波形如图2所示,假设储能电感电流IL1从0上升到ILm1时,VO1输出路储能电感平均电流IAV1等于目标平均电流IE1, 副边整流开关管SW1截止,其导通时间为ton1,此时原边电流Ip上升到Ipm1,原边主开关S1继续导通,由于副边整流开关管SW1截止,副边绕组W2上的电流变为零,输入电流Ip从Ipm1迅速下降到Ipd1;由于其他两路储能电感电流继续上升,输入电流Ip从Ipd1再次开始上升。

图2 变压器原边电流Ip和副边储能电感电流ILi波形示意图Fig. 2 Schematic diagram of the waveforms of transformer primary current Ip and secondary energy storage inductor current ILi
同理,VO2输出路储能电感电流IL2上升到ILm2时,其储能电感平均电流IAV2等于目标平均电流IE2,关断整流开关管SW2,其导通时间为ton2,此时原边电流Ip上升至Ipm2;由于整流开关管SW2截止,副边绕组W3上的电流为0;原边电流Ip从Ipm2迅速下降至Ipd2,由于VO3输出路储能电感电流继续IL3上升,原边电流Ip从Ipd2开始上升。
当VO3输出路储能电感电流IL3上升到ILm3时,其储能电感平均电流IAV3等于目标平均电流IE3,此时关断整流开关管SW3,其导通时间为ton3,由于副边三路整流开关管都已截止,此时应关断主开关管S1,原边电流Ip下降为零,让正激变换器T1进行磁复位。主开关导通时间ts等于最后截止的整流开关管导通时间ton3。为使得系统能正常磁复位,ts应小于T/2。
1.3 整流开关导通时间的计算
ARM对各路输出电压VOi(t)和输出电流IOi(t)进行实时采样,计算出各路的实时负载RLi(t)为
(1)
由各路输出期望电压VEi(t) (i=1,2,3),结合各路实时负载RLi(t),计算出各输出路目标平均电流IEi(t) (i=1,2,3)为
(2)
由于多路输出正激变换器工作在断续模式,储能电容Ci在一个周期内平均电流为0,所以使储能电感周期平均电流IAVi(i=1,2,3)等于目标平均电流IEi,即实现输出电压的有效控制。
储能电感峰值电流和平均电流,如图3所示。通过能量面积法可以将储能电感电流ILi(i=1,2,3)在储能电感充放电时间tri(i=1,2,3)内能量面积等效成储能电感平均电流IAVi在周期时间T内的能量面积[22-23],如式(3)所示:
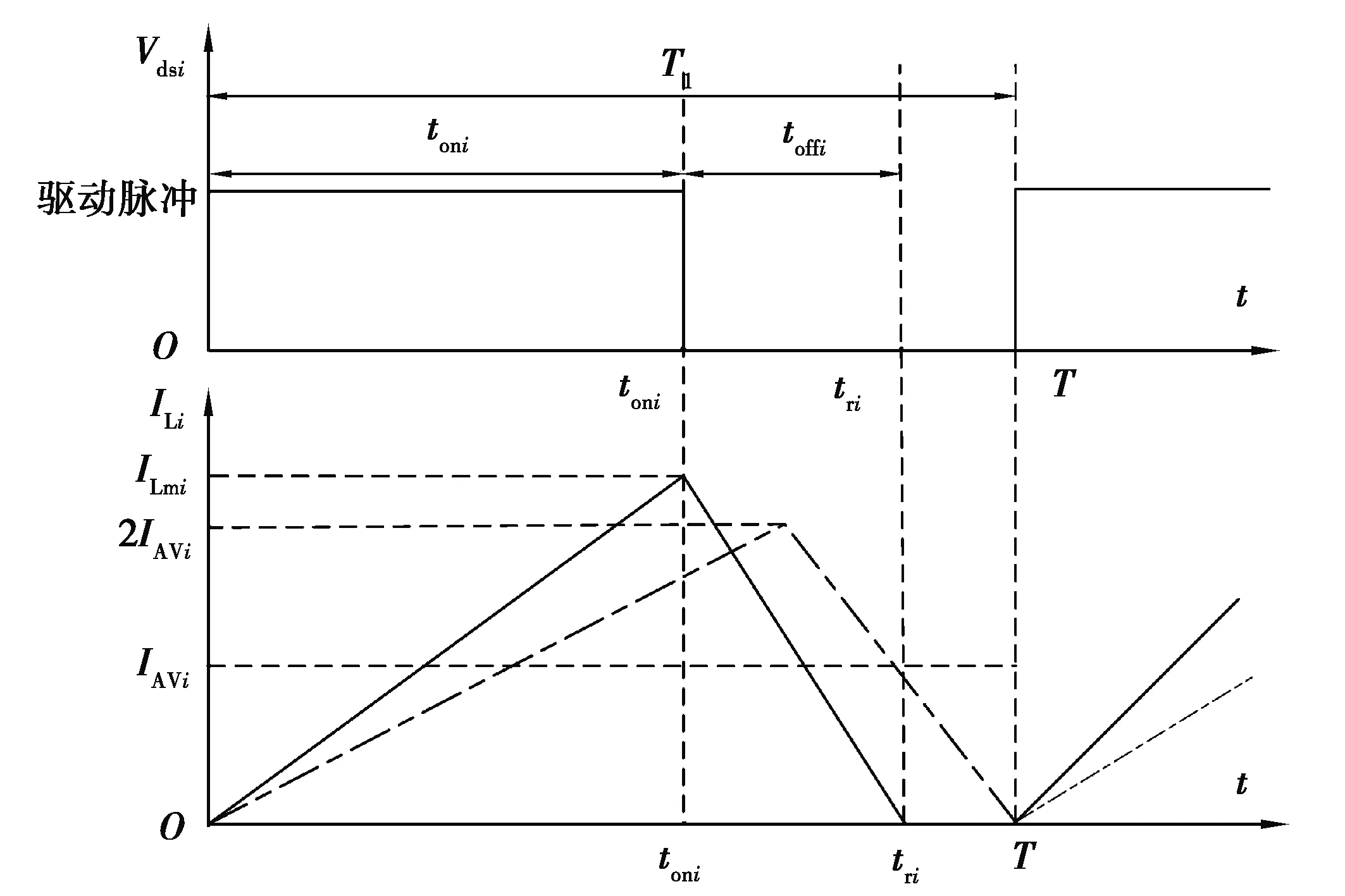
图3 储能电感峰值电流ILmi与平均电流IAVi示意图Fig. 3 Schematic diagram of the peak current ILmi and the average current IAVi of the energy storage inductor
(3)
式中, 储能电感充放电时间tri为储能电感电流上升时间和下降时间之和,ILmi(i=1,2,3)为储能电感的峰值电流。
根据伏秒平衡原理,储能电感电流上升时间与峰值电流ILmi之间的关系为
(4)
式中,toni为第i路输出整流开关管的导通时间。
当整流开关管关断时,储能电感电流下降时间toffi与峰值电流ILmi之间的关系为
(5)
式中,toffi为第i路输出储能电感电流下降时间。
联立式(4)和式(5),可得第i路储能电感充电时间与其放电时间的比例系数Ki(i=1,2,3)为
(6)
式中,ni(i=1,2,3)为变压器匝比。
联立式(3)和式(6)可得:
(7)
式中,T为开关管周期。
根据目标平均电流控制原理,将目标平均电流IEi代入式(7),并结合式(4)和式(6)可得:
(8)
获得第i路输出路整流开关管的导通时间toni为
(9)
在实际电路中需要考虑二极管的管压降和线路损耗影响,假设Vsr为主开关管导通时的管压降,VDri(i=1,2,3)为整流二极管Dri和整流开关管SWi的总压降,VDfi(i=1,2,3)为续流二极管Dfi和线路阻抗的总压降。可计算出第i路整流开关管导通时,续流二极管Dfi的阴极节点电压Voni为
Voni=(VS-Vsr)/ni-VDri。
(10)
由续流二极管的阴极节点电压Voni,结合压降VDfi和期望输出电压VEi,计算得到第i路整流开关管导通时,储能电感两端的压降VLi为
VLi=Voni-VEi-VDfi。
(11)
对式(9)进行修正,结果为
(12)
2 电路与程序设计
为了验证上述理论分析的合理性,搭建实例样机。实例样机的输入直流电压VS为48~72 V,第1路输出为24 V/2 Α,第2路输出为12 V/2 Α,第3路输出为5 V/1 Α。
2.1 硬件设计
硬件电路组成如图1所示,对其中的正激变压器参数、储能电感参数、主开关管驱动电路、采样电路进行了详细设计。
2.1.1 正激变压器设计
正激变压器开关频率为50 kHz,输入功率最大为90 W。选取合适的磁芯型号,其材质为PC40,规格为EE40,工作磁通密度ΔB=0.2T,磁芯截面积Ae=127.0 mm2。
为保证最小输入电压VS,min时,电路能正常工作,变压器原边绕组与副边绕组的匝比ni为:n1=1.33,n2=2,n3=4,nr=1,其中nr是磁复位绕组与原边绕组的匝比。
根据磁芯的参数计算出原边绕组匝数Np为
(13)
式中,ton,max为正激变压器能正常磁复位情况下的开关管最大导通时间。
由式(13)求得原边绕组匝数Np为16匝。由变压器匝比ni与原边匝数Np之间的关系,求得副边绕组和磁复位绕组匝数为:NS1=12匝,NS2=8匝,NS3=4匝,Nr=16匝。
2.1.2 储能电感设计
储能电感Li(i=1,2,3)确保多路输出正激变换器工作在断续模式下,计算出临界电感LCi(i=1,2,3)为

(14)
式中,IEi,max(i=1,2,3)为最大期望输出电流,Vf为副边整流管导通压降。
储能电感Li应满足输入电压为VS,min时,电路能够满载工作,此为最恶劣情况。计算出最恶劣情况下的最大电感峰值电流Ipi,max(i=1,2,3),最大峰值电流Ipi,max与最大期望输出电流IEi,max之间的关系为
(15)
联立式(6)和式(15)可得
(16)
由式(16)可获得最大电感峰值电流Ipi,max为
(17)
最后,储能电感Li须满足在最恶劣情况下,导通时间toni≤toni,max时,储能电感电流ILi能够上升到Ipi,max。满足其条件,得到储能电感Li为
(18)
由式(18)可确定三路输出储能电感值Li分别为14 μH、23 μH和 25 μH。
2.1.3 主开关驱动电路和采样电路设计
主开关驱动电路采用脉冲变压器隔离驱动[24],如图4所示,ARM产生的PWM波通过功率放大芯片MCP1402将高电平3.3 V,低电平0 V的脉冲波形,放大到高电平15 V,低电平0 V的脉冲波形,传送到脉冲变压器T2进行隔离驱动主开关管。
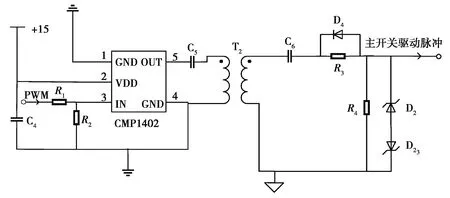
图4 主开关驱动电路Fig. 4 Main switch drive circuit
电压采样电路为分压电阻采样,如图5(a)所示,电压采样电路采用千分之一精密电阻分压和电压跟随器组成。电流采样电路采用CSM003A霍尔电流隔离采样芯片和外围电路组成,如图5(b)所示。CSM003A的采样精度为±0.7%,精密电阻R7的取值与霍尔电流传感器的匝数比以及ARM的端口安全电压有关。

图5 采样电路Fig. 5 Sampling circuit
2.2 软件设计
STM32F103C8T6是一款基于ARM内核的微控制器,其ADC模块分辨率为12位,ADC时钟速率最大为14 MHz,具有16个外部通道,支持内置多个定时器,能够同时输出多路PWM波。具有采样精度高、内置多个定时器、低功耗和DMA等特性,能够满足基于文中方法的多路输出正激变换器的设计要求(ADC分辨率位数≥10;ADC时钟频率≥4 MHz;ADC通道数≥7;PWM输出路数≥4)。
主函数的程序流程如图6所示。系统初始化完成后,对输入电压VS(t)、输出电压VOi(t)和负载电流IOi(t)进行实时采样,通过式(1)和式(2)计算出三路的实时负载RLi(t)和目标平均电流IEi,将参数导入式(12)计算出各输出路整流开关管的导通时间toni,其最大导通时间为tmax,主开关导通时间ts等于tmax;由于正激变压器有少量漏感和线路损耗无法避免,可以适当调节开关管导通时间toni,使得各路输出电压VOi更加趋近期望电压VEi,更新PWM波占空比Di(i=1,2,3),最后输出PWM波控制开关管的截止,实现各路输出电流的合理控制,以及各路输出电压VOi等于期望电压VEi。

图6 主函数的程序流程图Fig. 6 Program flow chart
3 实验结果测试
实验对各路输出的交叉调整率和输入电压调整率等进行了测试。
3.1 交叉调整率测试
设定输入电压VS为60 V时,VO1输出路带载不变,改变VO2和VO3输出路的负载值。观察输出电压VO1的变化情况如表1所示。
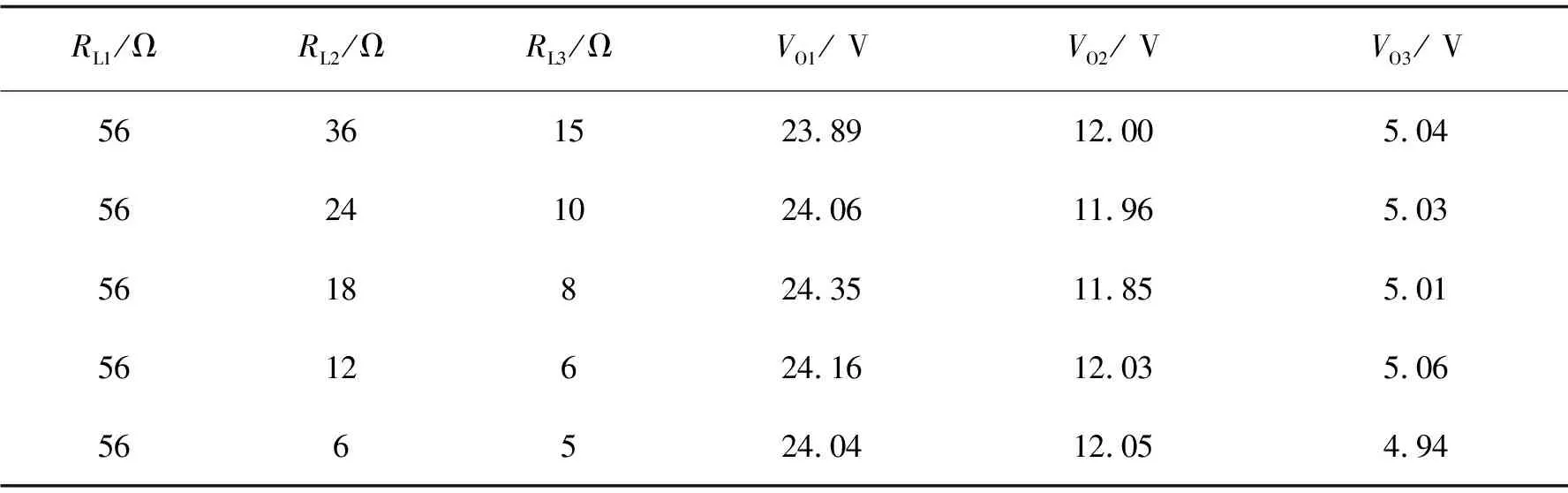
表1 VO1随VO2和VO3输出路负载变化的测试结果
由表1结果可以获得VO1输出路的交叉调整率为1.5%。同理,可以获得VO2受VO1和VO3输出路负载变化影响的测试结果,实验数据如表2所示。

表2 VO2随VO1和VO3输出路负载变化的测试结果
由表2可以获得VO2输出路的交叉调整率为1.4%。同理,获得VO3受VO1和VO2输出路负载变化影响的测试值,实验数据如表3所示。
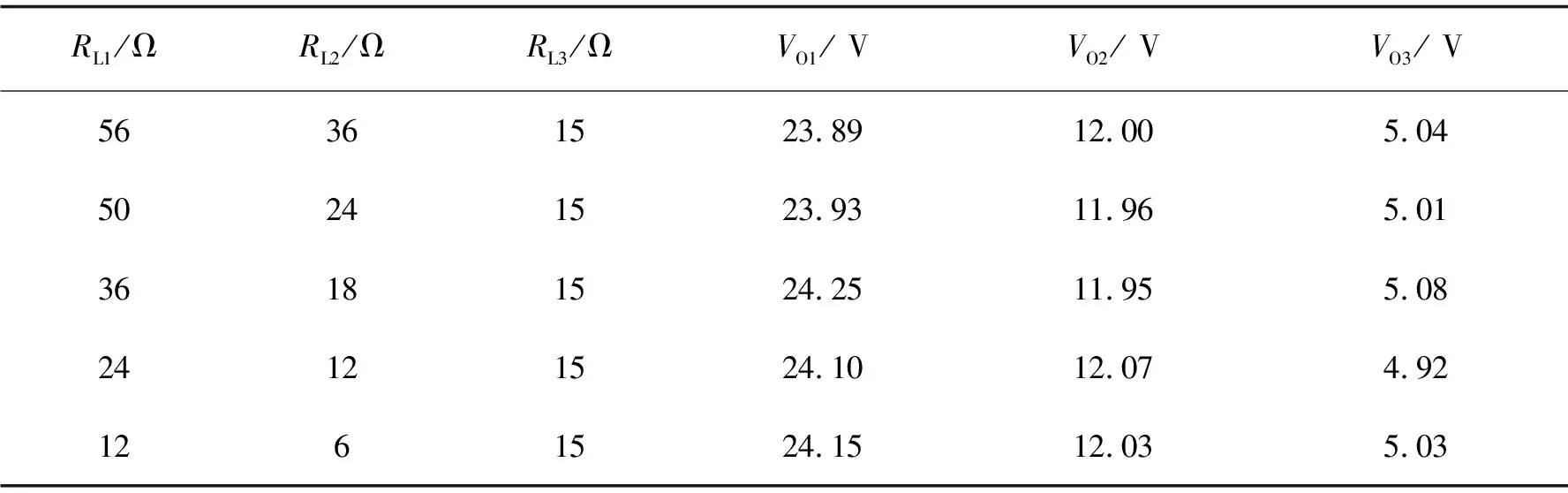
表3 VO3随VO1和VO2输出路负载变化的测试结果
由表3可以获得VO3输出路的交叉调整率为1.6 %。由表1、表2和表3可获得各输出路的交叉调整率不超过1.6%。将文中方法和参考文献中提到的其他控制方法作了比较,结果如表4所示。

表4 几种控制策略的交叉调整率对比
文中提出的目标平均电流法改善效果优于文献[12]、文献[13]、文献[16]和文献[17],与文献[19]改善效果相当,但是输出功率高于文献[19]中实例,且测试时输出功率变化值高于文献[19]。
3.2 输入电压调整率测试
在三路输出负载RLi不变的情况下,调节输入电压VS在48 ~72 V之间变化,得到三路输出电压VOi的变化情况,实验结果如表5所示。
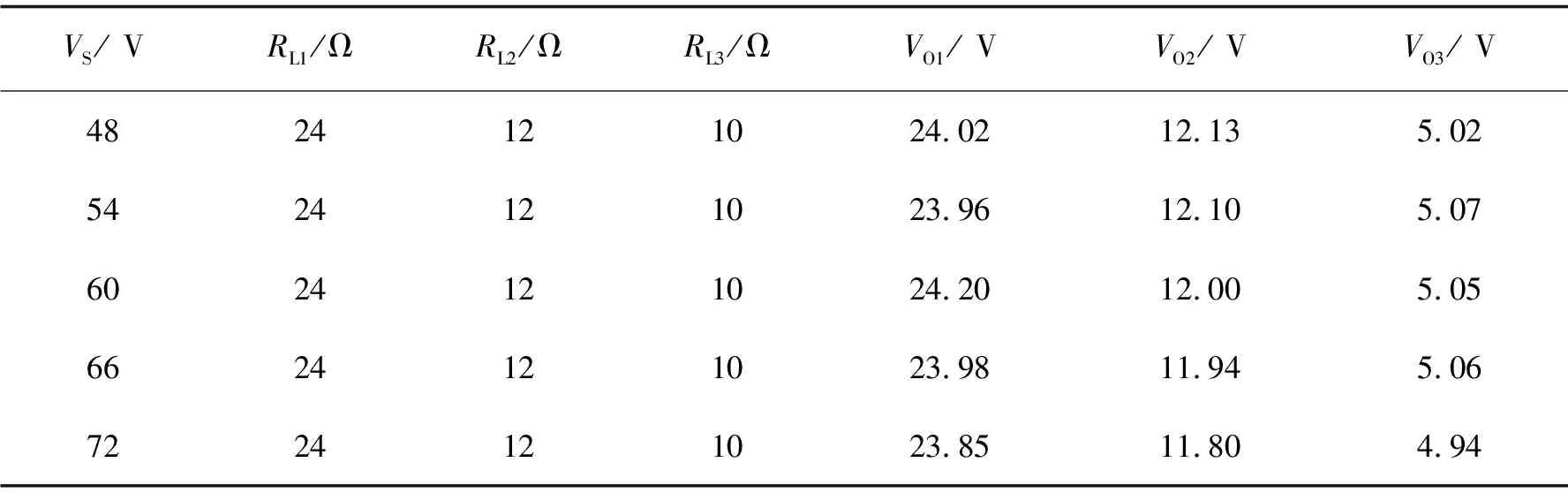
表5 输入电压调整率测试结果
由表5中数据可以得出VO1、VO2和VO3的输入电压调整率分别为0.9%、1.1%和1.4%。
综合以上测试数据可以得出,VO1的输出电压精度为1.5%,VO2的负载调整率为1.3%;VO2的输出电压精度为1.4%,VO3的负载调整率为1.2%;VO3的输出电压精度为1.6%,VO1的负载调整率为1.1%。
3.3 实验波形测试
在输入电压VS等于48 V的情况下,三路输出VO1、VO2和VO3的负载分别为56 Ω、24 Ω和10 Ω时,分别对主开关S1驱动波形、三路整流开关管SWi驱动波形、储能电感电流IL2波形和变压器原边电流Ip波形及输出电压VO2波形进行测试。
3.3.1 开关驱动波形测试
通过式(12),计算得到开关管导通时间ton1为4.4 μs,ton2为5.6 μs,ton3为8.2 μs,主路开关管导通时间ts为8.2 μs。测得主开关管驱动波形和三路整流开关管驱动波形如图7所示。由图7可知,整流开关管Swi的驱动波形分别为A、B、C,主开关管S1的驱动波形为D,可以测得整流开关管的导通时间toni分别为4.4 μs、5.5 μs和8.2 μs,主开关管导通时间ts为8.3 μs,与理论计算值基本一致。

图7 四路开关的驱动实验波形Fig. 7 Switch drive waveform
3.3.2 电感电流和输出电压波形测试
以VO2输出路为例,期望输出电压VE2为12 V,实验时接入实时负载24 Ω,目标平均电流IE2为0.5 A。由式(12)计算出ton2的理论值为5.6 μs,将ton2的理论值代入公式(4)获得储能电感峰值电流ILm2的理论值约为2.2 A。
实验测得原边输入电流Ip、储能电感电流IL2和输出电压VO2的波形分别如图8中E、F、G所示,与理论分析波形基本一致。整流开关管导通时间ton2为5.5 μs,储能电感电流IL2的峰值为2.18 A,都与理论计算值基本相符。同时,由图可测得输出电压VO2为11.96 V,与期望输出电压VE2也基本一致,可获得较高的电压精度。

图8 Ip、 IL2和 VO2的实验波形Fig. 8 Waveforms of Ip, IL2 and VO2
4 结束语
文中提出了一种低交叉调整率的多路输出正激变换器设计方法。由ARM根据硬件参数、实时输入电压、各路期望输出电压以及实时负载获得主开关和各路整流开关的合理导通时间并加以控制,实现各路输出电压等于输出期望电压,有效解决了交叉调整率问题。为使电路能在最恶劣情况下正常工作,详细分析了储能电感和正激变压器的设计方法,在有效改善交叉调整率的基础上,实现了较高的电压精度。

