基于基频的梅尔倒谱系数在车辆识别中的应用

李成娟，易 强，李宝清，王国辉

(1.中国科学院 上海微系统与信息技术研究所 微系统技术重点实验室，上海 201800； 2.中国科学院大学，北京 100049)

无线传感器网络凭借其通信能力强大、记录信息全面、无需人工值守等优点，广泛应用于军事、农业、商业等各个领域[1-2]。无线传感器网络通常由图像、声音、红外、震动传感器等几种类型的传感器构成[3]。声音传感器有不易被察觉、便于布设、不易受地形影响的优点，被广泛使用。

根据车辆行进过程中采集的声音信号，对野外车辆目标进行识别，一般分为2个步骤：1)提取声音传感器采集的声信号特征；2)设计分类器得到判别结果。目前常用的特征有基于小波包变换提取的特征，线性预测倒谱系数[4]，梅尔倒谱系数(MFCC, mel-frequency cepstral coefficient)[5]，基于经验模态分解提取的特征[6-7]等。其中，MFCC较常见，被广泛用于语种识别、说话人识别、声纹识别等领域，近年来被成功应用于车辆目标分类识别[8-10]。但由于MFCC对噪声敏感[11-13]，在车辆识别领域的应用场景受限。

为提高特征抗噪能力，增强特征稳健性，能够体现野外车辆信号自身特征，提出一种改进的MFCC特征。根据车辆目标信号的频谱特征，自适应增加车辆基频信息在特征中的比重。然后进行F比加权，以降低同种车辆类别特征间的区分度，增大不同车辆类别特征之间的差别，从而提高特征在野外环境下的鲁棒性。使用高斯混合模型(GMM, gaussian mixture model)作为分类器，检验识别效果。提取传统MFCC特征，基频自适应MFCC特征，加权基频自适应MFCC特征作对比试验，期望获得更高的识别准确率，为野外环境的车辆识别，提供一种鲁棒特征提取方法。

1 传统的MFCC特征

人耳对声音信号的感知，与频率呈非线性关系。随着声音信号的频率降低，人耳接收信号的能力愈发敏感[14]。为使人耳对信号敏感程度与信号频率呈现线性关系，MFCC参数将信号频谱作映射处理，映射后的刻度称作梅尔刻度。映射函数的表达式如下

(1)

式中：M(f)为梅尔频率；f为频率。

第一步，提取车辆目标声信号的MFCC，首先需要在时域尺度对其进行分帧、加窗、预加重等预处理。为减小频谱泄漏，窗函数选取旁瓣衰减较大的汉明窗。预加重，实际是让信号通过一个高通滤波器，目的是滤除车辆声音信号中的低频干扰成分，增加高频成分的比重[15]。

第二步，为了将信号从时域尺度转换为频域尺度，作快速傅里叶变换，且计算每帧信号的能量谱。

第三步，对能量谱进行三角滤波。梅尔三角滤波器由公式(2)计算得出。

(2)

式中：Hi(k)表示滤波器参数；fi表示三角滤波器的中心频率。滤波后取对数，得到对数能量。

最后，进行离散余弦变换，得到MFCC。为了获取动态信息，提取语音信号的MFCC特征时，通常包含动态差分步骤。与语音信号相比，车辆声音信号频带窄，周期性强，没有必要获取动态特性，因此特征提取算法省略动态差分步骤。

2 改进的MFCC特征

传统的MFCC在识别纯净声音信号时，可得到很好识别结果，但对噪声的敏感度很高，当采集的实际声音信号包含噪声信息时，识别效果易受干扰，难以预测识别效果是否符合实际需求。而且，当风力等级变化时，很容易造成训练样本集与测试样本集不匹配。为降低噪声对识别效果的干扰，减少应用场景的限制，对传统MFCC特征提取算法进行改进。

2.1 基频自适应梅尔倒谱系数

由于不同车型的传动系统、排气系统、发动机及其气缸数不同，不同车辆声信号的频域特性存在差异。不同车辆声信号频谱图如图1所示。 从图中可看出不同车型车辆声音信号的基频是不同的，因此车辆声音信号的基频可以作为车辆目标识别特征。将车辆声音信号的MFCC参数与基频特征结合，得到基频自适应梅尔倒谱系数。

图1 不同车辆声信号频谱图Fig. 1 Different vehicles’ spectrograms

提取传统的MFCC时，梅尔三角滤波器组中心频率根据梅尔刻度获得，随着频率提升，中心频率的密度逐渐降低。在野外情况风噪较大时，信号频谱中含有较多干扰频率，传统梅尔三角滤波器组有可能削弱基频在频谱中的比重，加大无关频率的干扰。为了更好体现车辆自身信号的频谱特征，在传统的滤波器组中，增添一个三角滤波器。该滤波器的中心频率为车辆信号的基频，通过此方法提取出来的特征称为基频自适应梅尔倒谱系数。改进的MFCC提取过程如图2所示。

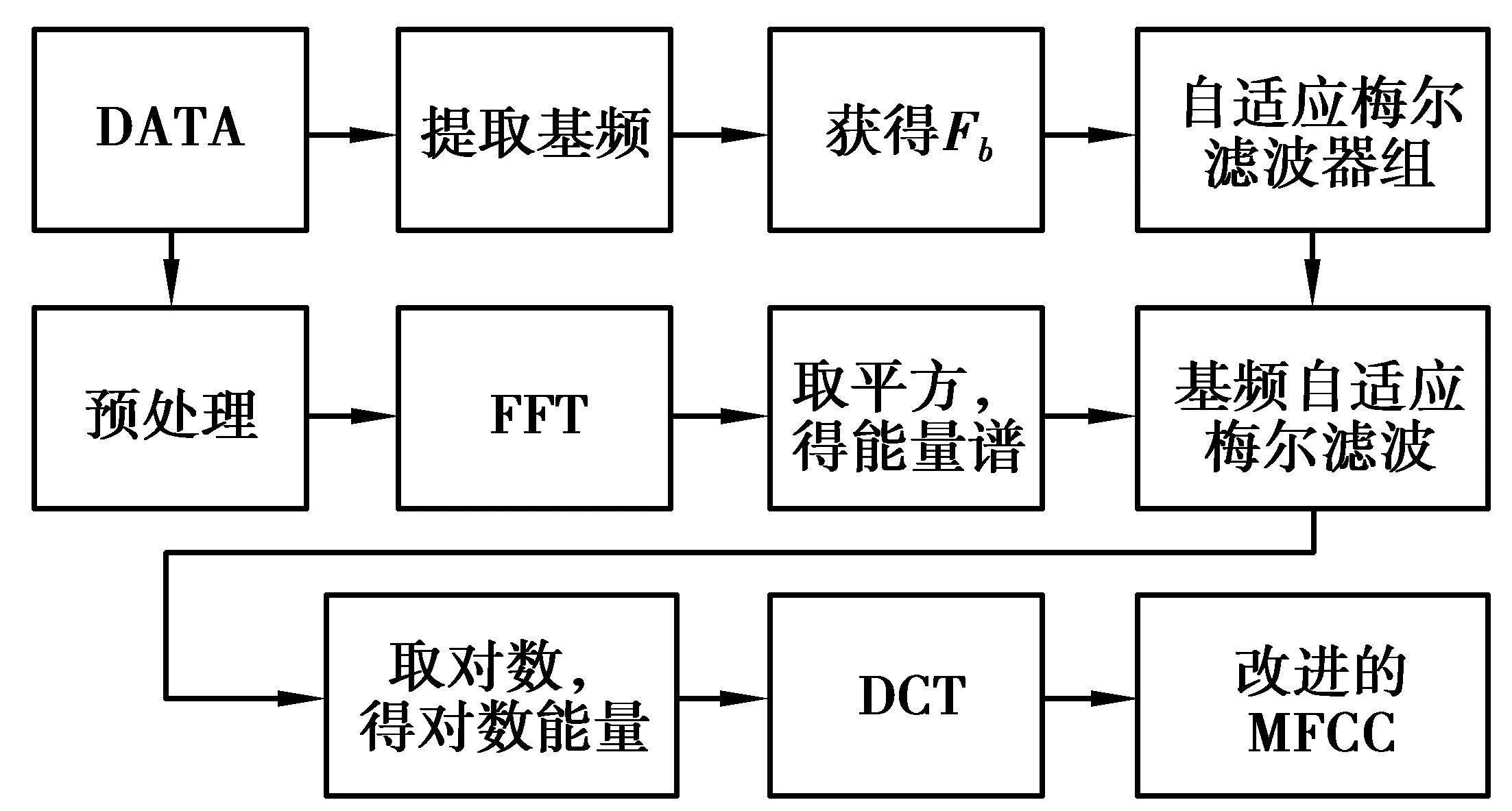
图2 改进MFCC特征提取算法框图Fig. 2 Flowchart of improved MFCC

自适应的梅尔三角滤波器组具体设计方法如下。假设传统梅尔三角滤波器组包含N个滤波器，其中心频率组成向量F=(f1,f2,…,fN)。提取车辆信号的基频fb，将fb与三角滤波器组的中心频率按升序排列，组合构成新的向量Fb=(f1,f2,…,fb,…,fN+1)。将Fb向量的各维分量作为滤波器的中心频率，代入式(2)，即可得到自适应的三角滤波器组。传统梅尔三角滤波器组与基频自适应的三角滤波器组如图3所示。

图3 三角滤波器组Fig. 3 Triangular filter-bank

为了得到基频自适应梅尔滤波器组，进一步获得基频自适应梅尔倒谱系数，需要选择合适的基频提取方法，准确提取车辆声音信号的基频。

2.2 基频提取方法

自相关函数法提取单基频时，为了降低共振峰干扰，需要先对信号进行带通滤波。然后对信号进行加窗、分帧，计算短时自相关函数。设车辆声音信号第i帧的时间序列为datai(m)，其短时自相关函数Ri(k)由式(3)得到

(3)

由于信号短时自相关函数周期与信号周期相同，因此基因周期可以取短时自相关函数的最大延迟量。对基因周期曲线进行平滑处理，使之通过中值和线性组合滤波，得到车辆的单基频信息。

图4 谱减法流程图Fig. 4 Flowchart of spectral subtraction

为了进一步满足野外环境的实际应用需求，将单基频提取算法改进为多基频提取算法。运动目标在行驶过程中生成的声信号，可由其发声主要部件产生的声信号表示，其余部件产生的声信号比较微弱，可忽略不计。履带车产生声信号的主要部件为履带和引擎，轻型轮式车和轮式装甲车产生声信号的主要部件是排气系统和引擎，因此车辆运动过程中的声信号可由2个主要成分表示，每个主要成分产生一条基频。下面简要介绍多基频提取算法。

首先提取车辆声信号的2条基频，可参照单基频提取方法。然后，将车辆的2个基频进行融合，得到一个新的基频fbnew(t)。设某条车辆声信号第t帧的2个基频，其中较大的数值为fb1(t)、较小的数值为fb2(t)，则fbnew(t)可由式(4)得到[18]

(4)

2.3 加权基频自适应梅尔倒谱系数

MFCC的每一维分量对表征特征的贡献率不同，为增加不同车型特征之间差距，使同一车型的特征更为紧凑，在基频自适应梅尔倒谱特征基础上，进行F比加权。F比参数，是在Fisher准则基础上提出的[19]，由类间离散度与类内离散度之比得到，可定量分析特征向量每一维分量有效性。设数据集包含M种车辆类别的车辆声音信号，其中第i个类型包含Ni条样本信号，则特征参数第k维特征分量的F比具体计算公式如下

(5)

特征参数中某维分量的F比参数数值越小，表明该特征分量在同类目标之间方差较大，在不同类目标之间方差较小，对表征信号特征的贡献率也越低。以F比为权重，对特征向量的每一维分量加权，能够削弱贡献率较低的特征分量干扰，提高贡献率较高分量的作用，从而提取更能体现不同车辆类别间差异的特征。

3 仿真实验

实验采用MATLAB R2015b平台仿真，样本信号采用ICS40720传声器设备进行采集，采样率为8 192 Hz。外场实验场景如图5所示，目标车辆从起始位置行驶到终止位置，麦克风便采集到一条完整的样本。

图5 实验场景图Fig. 5 Experimental scenario

仿真实验目的是根据野外无线传感器网络中声音传感器采集的信号，检验不同特征提取方法对车辆识别效果的影响。为了更贴近无线传感器网络的实际应用场景，声音传感器布设位置，距离道路中心不超过50 m，起始位置到终止位置的车辆行驶总长度限制在800 m以内。当野外风噪声非常大时，无线传感器网络中识别车型主要通过图像和震动传感器，声音传感器难以采集到有效车辆声音信号。因此去掉数据集中风力级在6级以上采集的声音信号，保留数据对应的风力级主要集中在1～5级。

3.1 实验过程

为验证改进的特征提取算法的实际识别效果，共采集硬土路、砂石路、水泥路及草地4种不同路面的车辆声音信号作为样本。车辆类型包含一种小型车，两种大型车，不同车型的行驶速度范围不同。小型车运动速度为25～60 km/h，代表车型为轻型轮式车，如卡车。大型车运动速度为10～20 km/h，代表车型为重型轮式车、履带车，如坦克。按照实际需求以及声音信号的特征，在实验中将车辆分为履带车、轮式装甲车和轻型轮式车3种类型。样本集中每种车辆类别样本数和总帧数如表1所示, 将样本数按照70%和30%的比例随机分为训练集和测试集，用于仿真实验。

表1 野外车辆样本数

采集数据后进行手工裁剪或拼接，由于存在人工误差，样本残留了部分噪声段。为获得更准确实验数据，对信号进行端点检测，得到有效运动目标数据后，再进行特征提取和分类识别。谱熵是声音信号的一种特征参数，对噪声不敏感，具有较好稳健性，因此，采用能熵比法对车辆信号进行端点检测。

检测到有效数据段后，首先提取维度为23的MFCC特征，然后提取维度为24的基频自适应梅尔倒谱特征，最后对其进行F比加权。

3.2 结果分析

表2 野外车辆识别结果

F比加权的基频自适应梅尔倒谱参数与传统的MFCC相比，识别准确率提高7.10%，漏警率降低7.10%，相对值降低56.62%，虚警率降低3.93%，相对值降低61.70%，有更高的鲁棒性，更适用于野外环境中车辆识别。

4 结 论

虽然F比加权的梅尔倒谱特征具有较好鲁棒性，但在进行特征提取之前，对野外采集的信号进行增强并降噪也非常重要。如何有效去除运动目标声信号中包含的噪声，将是下一步研究的重点内容。