基于聚类连通法的湍流拟序结构研究进展
董思卫 程 诚 陈坚强 袁先旭 , 李伟鹏
1 中国空气动力研究与发展中心, 空气动力学国家重点实验室, 四川绵阳 621000 2 上海交通大学航空航天学院, 上海 200240
1 引 言
虽然Richardson (1920)一百年前提出的湍流级串模型就已经预示着湍流中存在着多尺度和自相似的“湍流涡”(eddy)或者流动结构, 但直到斯坦福大学Kline 等 (1967)在实验中发现速度条带及伴随的猝发现象, 人们才真正认识到无序的湍流中存在“有序”的流动结构, 即拟序结构. 伴随着实验技术和高性能计算的发展, 拟序结构得到了人们越来越多的关注. 人们发现了诸如马蹄涡、速度条带、剪切层、上抛(ejections)和下扫(sweeps)等多种拟序结构(Robinson 1991; Adrian 2007; Jiménez 2012, 2018a;Wallace 2012; 许春晓 2015;郑晓静和王国华 2020), 这些结构极大地拓展了人们对湍流的认识.
湍流是一个在时间和空间上都存在很强间歇性的动力学过程, 李存标教授基于对转捩动力学过程的研究强调了从动力学角度研究湍流的重要性, 以级串现象为例, 他认为学术界对级串一直缺乏深入认识的根本原因是人们对湍流的动力学过程认识不足(李存标和佘振苏 2001). 实际上, 人们对拟序结构的研究一开始是从动力学角度出发的, 因为人们在湍流实验中首次观察到低速条带时就发现了它的准周期猝发过程, 即条带的抬升、振荡、破碎和再生. 即便如此, 相比于湍流的运动学特征, 人们对湍流动力学过程方面的研究要少很多, 且大多数研究往往基于被广为诟病的唯象性描述.
湍流的无序性要求必须从统计的角度来研究拟序结构以及它们在时空演化过程中的性质.为此, 就必须提取从Kolmogrov尺度到积分尺度的所有拟序结构并将它们以及它们的时空演化过程作为统计样本. 在高雷诺数湍流中, 对多尺度的三维拟序结构进行时空追踪和统计刻画一直是一个极大挑战.
聚 类 连 通 法(Jiménez et al. 2004)以 及 衍 生 的 拟 序 结 构 时 空 追 踪 法(Lozano-Durán et al.2014a)是从统计角度研究三维拟序结构以及它们时空演化过程的有力工具, 它实现了拟序结构与统计方法的深度融合, 摆脱了对流动结构唯象描述的局限, 极大加深了人们基于传统逐点统计结果对湍流的认识. 因此, 近几年来, 该方法在研究湍流拟序结构的运动学特征和动力学过程中得到了越来越多的应用(Lozano-Durán et al. 2012, 2014a, 2020; Dong et al. 2017, 2020; Cardesa et al.2017, 2019; Hwang & Sung 2018, 2019; Osawa & Jiménez 2018; Yoon et al. 2020; Cheng et al. 2020a,2020b). 聚类连通法是最简单的、基于数据的特征提取方法, 其他的湍流特征提取方法, 如基于算子(operator-based)的预解算子(resolvent operator) (McKeon & Sharma 2010)、基于数据(databased)的模 态分解方法, 如POD (proper orthogonal decomposition) (Lumley 1967, Rowley 2005,Towne et al. 2018), DMD (dynamic mode decomposition) (Schmid 2010, Jovanović et al. 2014,Noack et al. 2016), EMD (empirical mode decompcsition) (Huang et al. 1998)和基于图像(imagebased)的经验小波变换(Gilles 2013)等在湍流中也得到了广泛的应用.
对于湍流的动力学过程, 最直接的手段是采用时间解析的直接数值模拟(time-resolved direct numerical simulation, TR-DNS)或者实验测量技术(如tomographic time-resolved particle image velocimetry, Tomo-TRPIV)将流场以较高的采样频率保存下来, 然后观察某些流动特征的演化.
以往基于该思想对拟序结构时空演化的研究往往存在很多局限性或者对问题进行某些简化,例如Singer & Joslin (1994), Haidari & Smith (1994), Zhou 等 (1999), Suponitsky 等 (2005)在层流背景下研究了单个发卡涡的演化以及繁殖过程. Kim (1985)在低雷诺数槽道湍流(Reτ< 200)的近壁区追踪了单个马蹄涡的演化, 发现涡腿中有明显的涡量生成, 涡头部有较强的雷诺切应力.Bernard等(1993)追踪了流向涡的涡核, 发现流向涡是雷诺应力的主要贡献者. 采用最小计算单 元(Jiménez & Moin 1991), Hamilton等(1995)提 出 了 近 壁 湍 流 的 自 维 持 过 程, Flores和Jiménez (2010)观察了对数层的猝发过程中条带的演化. Yeung等(2015)在网格量为81923(约5500亿)的均匀各向同性湍流(Reλ≈ 1300)中研究了极端的强耗散和强涡量事件的生命周期.由于网格量极大, 他们只在28个Kolmogrov时间tη内保存了31个流场, 结果表明强耗散和强涡量事件几乎是同时发生, 同时, 那些ε/εrms> 1000和ω/ωrms> 1000的极端事件的生存周期只有5tη左右. 此外, 基于拉格朗日观点的涡面场方法(如Zheng et al. 2016, Zhao et al. 2016, Xiong &Yang 2019)以及精确相干态(如Jiménez et al. 2005, Sekimoto & Jiménez 2017, Yang et al. 2019)也可以用来研究湍流的时空演化过程.
本文对这些特征提取以及研究湍流动力学过程的方法不做对比, 感兴趣的读者可针对不同的问题, 选取合适的方法或者将聚类连通法与其他方法结合起来. 在下文中, 将从运动学和动力学两方面重点介绍人们利用聚类连通法在雷诺切应力结构、Townsend (1976) 的附着涡假设(attached-eddy hypothesis, 以下简称附着涡)和能量级串方面取得的重要进展.

2 拟序结构的提取和时空追踪
本节将详细介绍如何采用聚类连通法提取拟序结构并对它们进行时空追踪.
2.1 拟序结构的提取
聚类连通法是一个非常成熟的特征提取方法, 它与生活息息相关, 常见的医学图像分析、视觉跟踪中的前景检测、光学字符识别和人脸识别等都采用了该技术. 在提取湍流结构时, 为便于阐述, 采用简单的二维流场(图1)描述其过程. 对流场中的任意量Φ(图1(a)), 聚类连通法首先将流场二值化, 即将满足

的点(如图1(a)中等值线内的区域)赋1, 而其余的点赋0 (图1(b)), 然后将满足式(1)且彼此连通的空间点组成的连通域x= (x,y,z)提取出来并标记, 图1(c)中共提取了29个连通域, 连通域中的网格点以连通域的索引赋值. 式(1)中α为阈值, 对法向不均匀的壁湍流, 一般取Φrms为离壁面距离y的函数.Φ可以为雷诺应力、速度脉动、涡量脉动和亚格子能流等任意流场特征. 例如,若Φ为速度脉动, 称每个连通域构成一个速度结构. 当然, 该方法也同样适用于转捩(Chen et al.2021).

图1
图1中的步骤在三维流场中不容易直观地表示, 不过三维和二维结构的提取在算法上并无本质区别, 本文使用的算法为种子填充法(seed filling), 其核心是递归. 大体思路是:
(1)对网格量为(nx,ny,nz)的二值化三维流场逐点扫描, 当扫描到某个值为1的网格点(i,j,k)时, 初值为0的连通域索引(label)加1, 将索引赋值给(i,j,k)点, 并以该点为种子, 分别沿i,j和k方向继续搜索与其相邻且值为1的网格点, 对这些点赋予相同的索引, 同时对这些点的相邻点进行搜索和赋值(递归过程), 直至旁边所有的点值为0为止, 这时递归结束, 获得一个连通域;
(2)继续逐点扫描, 跳过那些值不为1的点, 当扫描到另一个值为1的点时, 索引值加1(即连通域数量加1), 重复步骤(1), 直至扫描完整个三维数组, 索引最后的值即为整个三维流场中连通域的总数.
当然, 还有其他算法, 这里不再赘述. 聚类连通法的计算量取决于满足式(1)的网格点数. 在表1中以提取某槽道湍流(网格量1.125亿)中的三维低速条带(即u(x) < −αurms(y))为例, 给出了采用种子填充法和Intel(R) Core(TM) i7-7700处理器提取不同阈值三维低速条带结构的计算时间(只考虑聚类连通法的时间). 即使对于约5 × 107的网格量, 该方法也仅需约2 s, 因此, 聚类连通法是一个非常经济实用的拟序结构提取方法.

表 1 采用聚类连通法(基于种子填充算法)在槽道湍流中提取三维低速条带的耗时
图2为采用聚类连通法在槽道湍流中提取的雷诺切应力结构和涡簇(vortex cluster), 显然,这些结构的大小和形态各异, 所有流场中的结构组成了数量可观的统计样本. 感兴趣的读者还可以在网站http://turbulentbeautycontest.appspot.com找到更多不同形态的三维结构.

图2
使用该方法时需要注意两点, 一是阈值α的选取, 阈值太小时会出现一个超大结构, 而阈值太大时, 连通域往往只有几个网格点, 这两种极端情况都不适合研究拟序结构的性质. 为避免α取值的随意性, Moisy和Jiménez (2004)引入了逾渗理论(percolation theory), 该理论具有定义临界阈值参数的能力, 被认为是处理无序系统及随机几何最好的方法之一(Stauffer & Aharony 1994). 阈值从零逐渐增加时, 原本低阈值时的较大连通域会分散为更多的小结构, 因此最大结构的体积与所有结构的体积的比值Vmax/∑V从1开始逐渐减小, 并在一定阈值范围内急剧下降, 这种骤降类似于渗流相变(percolation transition), 一般将阈值选在该区域内. 结构的数量N(α)随阈值的增大先增加后减小, 在“渗流相变”区域, 结构的数量大致在最大值Nmax附近. 下文中介绍的工作都表明, 在“渗流相变”区域, 拟序结构的统计特性没有本质不同.
另一个需要注意的点是平板湍流边界层中脉动量的定义, 当采用传统的雷诺分解时, 即使在湍流/非湍流界面(turbulent/non-turbulent interface, TNTI)以外的非湍流区, 也可能存在大尺度结构(Atzori et al. 2019). 为了避免得到非湍流区的虚假拟序结构, 以流向速度为例, 其平均量应当是离壁面高度y以及湍流/非湍流界面高度δTNTI的函数, 而不仅仅是y的函数, 因此, 脉动量应为相应地, 脉动量的均方根也是y和δTNTI的函数, 具体的实现方法可参考Hwang和Sung (2018)和Yoon等(2020) 的研究.
提取出三维拟序结构之后就可对其几何特性以及周围的流场开展统计研究. 最基本的几何特性包括体积V、外接长方体的边长(Δx, Δy, Δz)和重心位置(xc,yc,zc), 在壁湍流中还包括它们离壁面最近和最远的距离ymin和ymax. 此外, 还可以计算三维结构的分形系数以及亏格(Lozano-Durán & Borrel 2016)等.
对于三维拟序结构周围的流场特征, 一般可采用自适应条件平均获得, 即条件平均的窗口(长方体)大小与结构的大小成正比. 条件平均的流动参数可以为速度、涡量或者剪切等任意可反映流动机理的量, 下文中条件平均后的流场将以表示. 这一方法已被广泛采用(Lozano-Durán et al. 2012; Dong et al. 2017, 2020; Osawa & Jiménez 2018; Cardesa et al. 2019). 此外, 线性统计估计(Adrian & Moin 1988)也是获得平均流场的的一个重要方法(如Deng et al. 2018, Wang et al. 2021).
马德里理工大学(U. Politécnica de Madrid)的Jiménez (2004)最早将聚类连通法用在了湍流研究中, 这和他早年在计算机领域的工作有关. 1973年在加州理工学院应用数学专业获得博士学位并做短暂停留之后, 从1975年开始, Jiménez在IBM马德里科学中心工作了近15年, 主要从事图像的分割算法及应用研究, 涉及的图像涵盖了天文、生物和流体力学等多个学科. 期间代表性的工作包括位图与矢量图的转换算法及软件开发(涉及轮廓跟踪、线条细化和多边形逼近等技术) (Jiménez & Navalon 1982)、从湍流混合层实验胶片中提取流动结构并研究它们的时空演化特征(Hernan & Jiménez 1982)和基于湍流混合层实验的激光荧光图片对流场进行三维重构(Jiménez et al. 1985)等. 实际上, 基于实验图像或录像的流动特征提取至今仍是热点话题, 例如Zheng 等 (2019)根据可压缩平板边界层转捩过程中标量场的二维图像, 建立了壁面摩阻和标量流向倾斜角之间的关系, 并成功预测了壁面摩阻沿流向的变化. Ren等(2021)采用经验小波变换, 基于羽流和尾迹流的二维实验图像和直接数值模拟得到的平板边界层转捩前期流向速度和涡量的二维图像, 对流动进行了模态分解, 所得结果真实反映了流动特征.
由于早期计算机内存有限, 人们采用该方法提取三维结构时对数据是逐面处理的(Moisy &Jiménez 2004, del Álamo et al. 2006), 后来, 随着计算机内存的极大提升, Lozano-Durán等 (2012)对聚类连通法的算法进行了大量的优化, 极大提高了计算效率. 如今, MATLAB的bwlabel, bwlabeln和bwconncomp函数可以轻松地提取连通域, 此外, Python的图像处理包SciKit-Image也有类似功能, 不过读者们在使用这些工具时需注意它们对周期性边界的处理.
2.2 拟序结构的时空追踪
当保存流场的时间间隔Δt足够小时, 图2中的三维结构在相邻时刻变化很小, 因此空间上会有重叠. 基于此, Lozano-Durán和Jiménez (2014a) 借鉴图分析(Needham & Hodler 2019)开发了基于连通域重叠的三维拟序结构时空追踪方法, 该方法可以对从Kolmogrov尺度到积分尺度的所有三维结构进行追踪, 且不限于结构的类型, 该方法当然也可退化为对低维流动特征的追踪. 该方法主要分为三步.
首先, 计算相邻时刻拟序结构的空间重叠. 如果t时刻的某一拟序结构与t− Δt时刻多个拟序结构有空间重叠, 可认为该结构是t− Δt时刻与之重叠的结构合并而来. 反之, 若t时刻的某一拟序结构与t+ Δt时刻的多个拟序结构有空间重叠, 可认为该结构在t+ Δt时刻分裂为多个结构. 当然, 也有些拟序结构与相邻时刻的结构没有重叠, 这时, 该拟序结构被称为孤立结构, 因而无法被追踪. 在正式进行长时间的时间分辨直接数值模拟之前, 需要综合考虑孤立结构的占比以及所需存储空间的大小, 以确定合适的时间分辨率Δt. 如果追踪的是大尺度或超大尺度结构, Δt则可以显著增大.
其次, 在得到所有相邻时刻拟序结构间的重叠情况之后, 就可以在时间方向上采用聚类连通法, 将所有相邻时刻有空间重叠的拟序结构放入一个图(graph)中, 在图算法中, 这类图叫做连通图(connected graph). 图3(a)为两个拟序结构在从生成到消亡的过程中构成的一个图, 在图中,如图3(b)所示, 每一个三维拟序结构被虚化为一个节点(node), 相邻时刻彼此有重叠的结构(节点)构成一个边(edge或link).
最后, 将graph中的结构划分到不同的分支(branch)中. 每个分支中相邻时刻两个结构的相对重叠率Ro= |V2−V1|/Vo(体积为V1(t)和V2(t+ Δt), 体积重叠为Vo)对彼此都是最小的(即相邻时刻体积变化小、空间重叠多), 因此每个分支都可视为某个结构的演化过程. 这里需要注意的是结构的分裂与合并, 如图3所示, 当某一个结构由上一时刻多个结构合并而来时, 它就有多个“引入边”(incoming edge),Ro最小的那个边所在分支为主引入分支(primary incoming branch),其他边所在分支则在该时刻终止. 同样地, 当某一结构在下一时刻分裂为多个结构时, 该结构有多个“外出边”(outcoming edge),Ro最小的那个边所在分支为主外出分支(primary outcoming branch), 其他边所在分支则代表碎片的演化. 那些包含拟序结构从生成到消亡整个过程的分支为主分支(primary branches), 只有主分支的生命周期才有明确的定义. 关于追踪方法更多的细节及其验证可参考Lozano-Durán和Jiménez (2014a)及其补充材料.

图3
以上步骤使得每个三维结构的时空演化过程成为统计样本, 从而使得对三维拟序结构从生成到消亡时空演化过程的统计刻画成为可能.
在高雷诺数湍流中, 要实现对每个拟序结构的时空追踪, 所需的内存是极大的, 对存储空间的需求也是巨大的, 特别是需要保存瞬时流场时(如速度及其梯度等). 图4为Reτ≈ 4200的槽道湍流中瞬时的涡簇和雷诺应力结构, 它们是非常复杂的, 类似这样的快照共有一万多个, 涡簇和雷诺切应力结构的总数都高达8 ~ 9亿, 覆盖了从Kolmogrov尺度到积分尺度的整个范围. 为节省存储空间, 在雷诺数较高时(Reτ≈ 2000和4200), Lozano-Durán和Jiménez (2014a)只以高时间分辨率保存了拟序结构的信息, 而瞬时流场则非常有限. 此外, 在保证能够解析大尺度结构的前提下(Lozano-Durán & Jiménez 2014b), 尽量减小计算域的大小(Lx/h= 2π,Lz/h= π), 并通过巧妙的设计将不同阈值的雷诺切应力结构和涡簇信息以“INTEGER 2”的形式保存在同一个文件中, 文件中只有零和非零两种整形值, 因此文件得以进一步压缩. 即便如此, 最终的存储量也达到了上百TB.

图4
由于近年来人们已将目光转向了外层的大尺度和超大尺度结构, Vela-Martín等(2019)进一步提出了在高雷诺槽道湍流中时间解析大尺度结构的低存储GPU-MPI混合计算方案. 他们采用高分辨率开展直接数值模拟, 但以较低的时空分辨率保存大尺度结构的信息和滤波之后的流场. 该方案可将存储空间减小三个量级, 为研究大尺度和超大尺度结构的时空演化提供了可能.
图5(a)为对Reτ≈ 4200的槽道湍流中所有时刻的涡簇进行时空追踪后所得的一个图中涡簇随时间的演化, 图5(b)为图5(a)中组成graph的分支之间的联系, 其中实线表示分支, 蓝色和红色虚线分别表示结构的分裂与合并. 由此可见, 三维拟序结构的时空演化是非常复杂的. 图5(c)为上抛在一个主分支中随时间的演化, 类似这样的分支一共有100多万(Lozano-Durán & Jiménez 2014a).

图5
需要注意的是, 以上拟序结构的提取和时空追踪只是采用聚类连通法研究拟序结构性质的前提, 针对特定的物理问题, 读者们还需要进一步编写不同的后处理程序, 深入挖掘所提取的湍流结构及其演化过程蕴含的物理机理是湍流研究者需要深入思考的问题.
3 拟序结构的运动学特征
本节将主要介绍聚类连通法在涡结构、雷诺切应力结构和速度条带的运动学特征上取得了哪些新的认识, 当然, 在下文中将会看到, 这些结构是彼此联系的, 而不是孤立的.
3.1 涡结构
Moisy和Jiménez (2004)在Reλ= 168的均匀各向同性湍流中提取了三维强涡量(|ω(x)| =结构, 并刻画了它们的几何特性和空间分布, 这是聚类连通法首次用于提取三维流动结构. 他们之所以同时研究这两种结构是因为Jiménez等(1993)和Pumir (1994)的结果表明涡管边缘存在着较强的剪切.
他们采用盒计数法(box-counting method)计算了两类结构的分形维数Df以及特征长度r1,r2和r3. 对每一个体积为V的三维结构, 外尺度r3和内尺度r1分别为该结构最小外接正方体和最大内切正方体的边长,r2=V/(r1r3)没有实际的物理意义, 但比值(r1/r2,r2/r3)可以大致确定三维结构的形状. 分形维数和(r1/r2,r2/r3)表明涡量结构随着阈值增大从块状(sheet)或者丝带状(ribbon)变为管状或“蠕虫”状(worm), 而强剪切结构则维持块状或者丝带状. 他们发现无法通过三维强涡量(剪切)结构的分形维数来描述强涡量(剪切)场整体的分形维数, 这是人们首次对三维梯度场的分形特性开展研究, 在此之前, 人们对诸如湍流/非湍流界面、标量或速度等值面等的分形特性虽已开展大量研究, 但绝大多数工作都是对二维流场的分析(黄真理 2000), 缺少对三维流场及其梯度分形特性的研究.
除此之外, 通过对比三维结构重心和随机Poisson点集的分布特性, 他们发现这些三维结构在空间的分布并不是随机的, 而是比Poisson点集更紧凑. 这方面的研究进一步演化为对三维拟序结构之间距离和相对位置的刻画(见3.2节).
在壁湍流中, 自从Perry和Chong (1982)采用随机分布的发卡涡复现了壁湍流对数层中的统计特征之后, 发卡涡一直是研究热点之一. 21世纪初, 根据平板湍流边界层中的实验观测结果,Adrian等(2000)提出了著名的发卡涡包模型. 在该模型中, 流向一连串的壁面附着的发卡涡以几乎相同的对流速度向下游运动. 在涡腿(流向涡量主导)的诱导下, 发卡涡下方形成了大尺度低速条带. 然而, 这个三维的发卡涡包模型是通过研究二维流场推测得到的, 在湍流中实际上很难发现完整的发卡涡. 因此, del Álamo等(2006)直接采用脉动速度梯度张量的判别式(该判据对空间分辨率要求较高)提取并研究了Reτ≈ 2000的槽道湍流中的三维涡簇, 这一工作奠定了用聚类连通法研究壁湍流中拟序结构的基础.
图2给出了槽道湍流中典型的涡簇, 图6为这些涡簇体积的概率密度函数与ymin和ymax的关系, 很明显, 涡簇可以分为壁面附着(wall-attached,ymin+< 20)和壁面分离(wall-detached,ymin+>20)两类. 后面将会看到, 区别壁面附着和分离的法向临界高度并不是固定的(取决于结构类型和壁面条件等), 一般来说壁面附着拟序结构的ymin≈ 0, 因此yc≈ Δy/2.

图6
由于缓冲层内当地雷诺数y+很低, 几乎没有尺度分离, 且当时近壁区已得到了较充分的认识, 他们便重点研究了那些在对数区的壁面附着涡簇(ymin+< 20且ymax+> 100). 在下文中如无特别说明, 提到的壁面附着拟序结构的ymax也都在缓冲层以外.

以ns≈ Δy−3衰减, 其中N(Δy)为高度为Δy的结构数量,Nf为流场数量,Lx和Lz分别为计算域的流向和展向长度, 在槽道中, 由于存在两个壁面, 因此存在系数2. 以上结果表明壁面附着的涡簇直观上非常类似于具有层次结构的附着涡, 这为后人逐渐揭示抽象的附着涡奠定了基础.
为揭示壁面附着涡簇周围的流动特征, 他们对壁面附着涡簇周围的流场做了三维自适应条件平均. 条件平均结果表明(图7), 涡簇位于斜坡状的大尺度低速条带(u' < 0)上游, 它与强上抛事件(u' < 0,v' > 0)密切相关, 周围存在很强的剪切层和雷诺切应力. 人们在实验中也观察到了类似的斜坡状低速条带(Adrian et al. 2000, Christensen & Adrian 2001), 并将其归因于发卡涡串的诱导. 三维结果(图8)表明低速条带为锥状, 涡簇的两侧各有一个比低速条带要短很多的高速条带(u' > 0).v'和w'的合矢量表明在低速条带的两侧有一对涡量相反的大尺度流向涡. 在(rx,rz)截面上, 低速条带的宽度和长度满足rz≈rx1/2, 这与该槽道湍流对数层中流向脉动速度预乘谱kxkzΦuu反映的波长间的关系λz≈λx1/2是一致的(del Álamo et al. 2004). 注意图7和图8中条件平均窗口的长度是以yc也就是Δy/2无量纲化的, 因此统计平均意义上, 低速条带的长度是涡簇高度的50倍以上, 而单个涡簇无法在其生命周期(通过法向速度的频率−波数能谱估计)中在下游诱导如此大尺度的低速条带. 他们认为涡簇是下游大尺度低速条带的果, 而非因. 其下游的大尺度低速条带则是由多个高度与流向位置成正比的涡簇诱导形成的, 这与近壁区的自维持过程是类似的.

图7
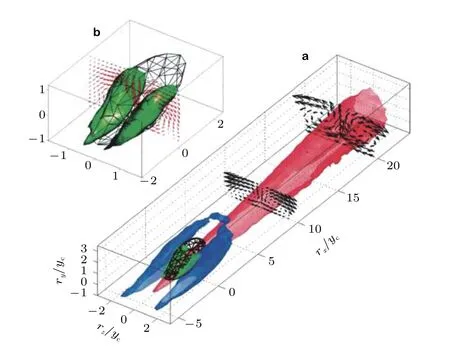
图8
注意图8中绿色等值面为条件平均流场的速度梯度判别式等值面, 它们类似于发卡涡的涡腿. 虽然对低速条带与涡簇之间因果关系的理解有所差别, 但del Álamo等(2006)得到的涡簇−低速条带和Adrian等(2000)的发卡涡串−低速条带模型在运动学上是一致的.
del Álamo等(2006)还发现, 涡簇的生存周期很短, 它们不太可能是从近壁区生成并逐渐向远壁区生长而成, 而是在当地生成的. 为了进一步探明大尺度涡簇的产生机制, 一年之后, Flores等(2007)对比了Reτ< 674的槽道湍流中光滑和粗糙壁面条件下外层(outer layer)涡簇的性质,结果发现虽然粗糙壁面改变了近壁区的统计特性, 却几乎不改变涡簇的性质: 它们还是存在壁面附着和壁面分离两类, 壁面附着涡簇的几何特性及周围的统计平均流场与光滑壁面条件下的非常接近. 他们的结果表明大尺度涡簇不是“自下而上” (bottom-up)形成的.
最后, 虽然几何上一些壁面附着涡簇贯穿了整个对数层, 但是后来Dong等(2017)发现在Reτ≈2000的槽道湍流中, 壁面附着涡簇仅占所有涡簇体积的10% ~ 15%, 且随雷诺数增加这一比值有减小的趋势, 因此用它们来研究大尺度结构(very large scale motions, VLSMs)可能不太适合. 实际上, 这些壁面附着的涡簇中包含的流动信息是小尺度的, 这是由提取涡簇的定义决定的. 此外,槽 道(del Álamo et al. 2006, Lozano-Durán et al. 2012)和 统 计 平 稳 均 匀 剪 切 湍 流(Dong et al.2017)中涡簇的内尺度r1都不随外尺度r3变化, 约为5η, 涡丝的直径约为η也得到了其他学者的证实(Jiménez & Wray 1998, Tanahashi et al. 2001, Pirozzoli et al. 2008, Stanislas et al. 2008), 这也从侧面说明大尺度涡簇其实是由多个小尺度的涡丝缠绕而成的.
3.2 雷诺切应力结构
雷诺切应力u'v' 代表单位质量流体的动量u' 在法向的传递, 它和平均剪切S= d〈u〉/dy一起构成了湍动能的生成项, 它还是壁面摩阻的主要贡献者(Renard & Deck 2016, Li et al. 2019). 此外, 对亚格子雷诺应力的正确模拟是大涡模拟的关键之一. 因此, 深入研究雷诺切应力具有重要的学术和工程意义.
对于雷诺切应力, 人们往往采用象限分析方法(quadrant analysis), 即根据流向和法向脉动速度u'和v'的符号, 将其分为Q1 (u' > 0,v' > 0), Q2 (上抛,u' < 0,v' > 0), Q3 (u' < 0,v' < 0)和Q4 (下扫,u' > 0,v' < 0)(Wallace et al. 1972, Willmarth & Lu 1972, Lu & Willmarth 1973), 其中, 对湍动能贡献最大的Q2和Q4受到了人们极大的关注. 然而, 以往对雷诺切应力的研究局限于各象限的雷诺切应力在法向的一维分布或者二维条件平均流场(Jeong et al. 1997, Schoppa & Hussain 2002, Ganapathisubramani 2008), 从未涉及对三维雷诺切应力结构的定量刻画, Wallace (2016)对该方法在过去四十多年的应用做了详细介绍.
Lozano-Durán等(2012)首次研究了Reτ= 2000的槽道湍流中的三维雷诺切应力结构, 结果表明, 上抛和下扫也可以分为壁面附着和壁面分离两类. 其中壁面附着的上抛和下扫占它们总体的80%, 它们几何上是自相似的
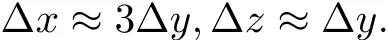
它们的法向分布密度随高度的衰减比壁面附着涡簇要慢(ns≈ Δy−2). 如图9为一个超大尺度(superstructure)的壁面附着Q2, 该结构在法向已超过槽道半高, 长度约为20h. 值得一提的是, 在2013年的美国物理学会流体力学分会上, Lozano-Durán还展示了3D打印的超大尺度雷诺切应力结构, 从而第一次使得湍流中的拟序结构触手可得.
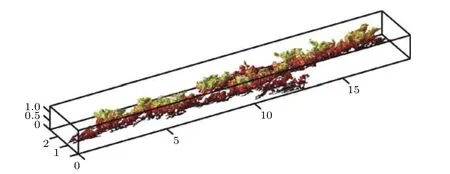
图9
他们计算了壁面附着结构在流向和展向的相对距离δx和δz(详见Lozano-Durán et al. 2012中公式6.1和6.2). 计算时, 他们只考虑那些大小接近的结构之间的距离, 即1/2 < Δy(i)/Δy(j)< 2,其中i和j表示结构的类型, 例如i= 2表示Q2. 图10为δx和δz的联合概率密度函数, 虚线和实线等值线分别表示相对于在(δx,δz) = (0, 0)处的参考结构, 找到其他结构概率较低和较高的地方. 很明显, 同一种类型的拟序结构(例如上抛与上抛之间)在流向是一连串出现的(图10(a) ~图10(c)). 上抛和下扫则是在展向成对出现的(图10(d)), 涡簇大致与上抛重合(图10(e)), 这与del Álamo等(2006)的统计平均流场是一致的. 注意相对距离δx和δz是绝对距离除以结构的特征长度d= (Δx2+ Δz2)1/2. 图8的结果表明结构间的距离与其大小是自相似的, 即彼此间的距离与它们的大小成正比. 值得一提的是, 最近Encinar和Jiménez (2020)关于猝发动力学过程的研究结果表明, 上抛和下扫的成对出现是同时的.
图10 (d)中Q2与Q4之间的相对位置与Adrian等(2000)的发卡涡包模型反映的是不一样的, 在该模型中, Q2位于Q4的下游. 实际上, 早在直接数值模拟刚兴起不久, Moin (1987)就在xz平面上观察到u和v的正负脉动在展向都是交替出现的. 后来, Robinson (1991)指出, 上抛并不需要一对反向的流向涡生成, 而且也很难发现一对反向的准流向涡, 他认为一个准流向涡就可以生成Q2和Q4, 且它们应该是展向成对出现的, 而不是流向. 他还指出人们在xy平面上之所以会得到Q2和Q4在流向成对可能是因为Q2和Q4在流向的错位, 或者说条带的蜿蜒导致的, 这也说明二维的结果是不全面的.
基于图10(d)的结果, 他们对展向成对的壁面附着上抛−下扫(Q2−Q4 pairs)周围的流场做了自适应条件平均, 图11(b)为瞬时的Q2(绿色)、Q4(蓝色)和涡簇(银灰色), 条件平均的结果如图11(a)所示,等值面为网格点属于不同结构的概率密度. 涡簇大致位于Q2和Q4 中间, 但更接近前者. 虽然计算统计平均流场的Q2和Q4 尺寸是接近的(图11(a)), 但和Q2关联的低速条带比与Q4 关联的高速条带要短的多(图11(c)), 且前者几乎被后者包了起来(图11(d)).

图10
相比以往对单个拟序结构的研究, Lozano-Durán等建立了上抛−下扫−涡簇综合体, 揭示了雷诺切应力、涡簇、速度条带和大尺度流向涡之间的关系. 他们认为, 上抛和下扫并没有本质的区别, 都同属于一个大尺度(相对于上抛和下扫)准流向涡(见图11(d)中的矢量图), 该流向涡的直径与Q2(Q4)的大小成正比. 该模型与Robinson (1991)的观点是一致的, 但流向涡不再局限于近壁区. 由于壁面附着的上抛和下扫是自相似的, 且具有层次结构, 因此, 图11(d)中的流向涡实际上也是多尺度和自相似的壁面附着结构, 动量在不同尺度的结构之间传递(Jiménez 2012), 这极大简化了人们对剪切湍流中雷诺切应力的认识. 注意这里的流向涡不是指采用ωx提取的结构,涡量是流场中的小尺度信息. 上抛和下扫在展向成对出现反映了高、低速条带之间的关系(Moin 1987, Sillero et al. 2014), 本质上是连续方程的体现.

图11
和壁湍流类似, 统计平稳均匀剪切湍流中也有猝发现象(Pumir 1996), 虽然统计平稳均匀剪切湍流中的猝发是有限计算域引起的非物理现象(均匀剪切流动本质上是无界的), 但Sekimoto等(2016)发现统计平稳均匀剪切湍流与槽道湍流对数层中的统计特性非常接近, 特别是以剪切时间无量纲化的猝发周期(都约为20 ~ 30S−1). 由于绝大多数的雷诺切应力能都是在猝发过程中产生的, 那么在有壁面和无壁面的两种剪切湍流中雷诺切应力有什么异同呢?Flores等(2007),Mizuno和Jiménez (2013), Tuerke和Jiménez (2013)的结果表明对数层的统计特性并不是由壁面决定的, 而是由平均剪切决定的, 基于此, 本文作者(Dong et al. 2017)将统计平稳均匀剪切湍流(Reλ= 100, 250)和槽道湍流对数层(Reλ≈ 100)中的雷诺切应力结构做了详细对比, 并进一步完善了上抛−下扫−涡簇综合体.
图12为雷诺切应力结构之间的最短距离r与特征长度d= (Δx2+ Δy2+ Δz2)1/2之间的关系.当d< 50η时,r约为常数, 而当d> 50η时,r与d成正比. 有意思的是, Q4(Q2)与Q4(Q2)的最短距离以Kolmogrov长度η标度(r/η ≈ d/η), 而Q2与Q4的最短距离却以Taylor长度λ标度, 且r与d不再是自相似的, 而是r/λ≈ (d/η)2/3. 值得注意的是, 槽道湍流中壁面分离的雷诺应力结构(ymin+> 100)之间的最短距离和统计平稳均匀剪切湍流中非常接近.

图12
图13为雷诺应力结构之间相对位置的三维概率密度函数. 图13(a)表明, 相对参考下扫(位于坐标原点), 在其上游和下游找到其他下扫的概率比较高, 但是上下游的高概率区相对流向是向下倾斜的(倾斜角约为45°), 上抛与上抛之间的相对位置呈类似的结果. 而Q1(Q3)与Q1(Q3)之间相对位置的概率密度函数等值面相对流向是向上倾斜的(倾斜角约为45°). 他们认为最可能找到与参考雷诺应力结构同类的结构的位置与定义雷诺切应力的脉动速度矢量方向一致. 以(u',w')定义的雷诺切应力结构之间的相对位置印证了他们的观点.

图13
图13(b)表明, 相对参考上抛, 找到下扫的高概率区成倒U状, 该区域与流向约成45°角, 由于对称性, 相对参考下扫, 找到上抛的高概率区成U状. 图13(b)中高概率区在展向的对称性是由流动本身的性质决定的, 并不代表上抛和下扫以三体(下扫−上抛−下扫)的形式出现, 若和图10(d) ~ 图10(f)一样将z> 0指向离参考结构最近的另一类型结构, 高概率区将只在z> 0一侧, 即上抛和下扫大概率是展向成对出现的, 这与槽道湍流中壁面附着的上抛和下扫是一致的(图10(d)). 图13(b)同时也表明, 也有小部分下扫出现在上抛的斜上方, 后面将会发现, 这一区域存在较高的剪切. 值得一提的是, 槽道湍流中壁面分离雷诺应力结构之间的相对位置和统计平稳均匀剪切湍流中是一致的, 而对于壁面附着的上抛和下扫, 由于壁面的约束, 下扫(上抛)不可能出现在上抛(下扫)的斜上方, 而只能出现在侧方. 由于图12中最小距离的标度律不同, 图13(a)和图13(b)中的相对距离为不同长度尺度无量纲化的结果.
统计平稳均匀剪切湍流中上抛−下扫−涡簇综合体如图14(a)所示, 图14(b) ~ 图14(c)为Q2 ~Q4对中心zy截面上的平均流场, 图14(d)为{∂yu'}的等值面. 和槽道中壁面分离结构类似,图14(a)中的结构几何上趋近各项同性. 实际上, 槽道中壁面附着结构流向的大拉伸比是其近壁部分导致的. 由于流动是均匀的, 涡簇对上抛和下扫没有偏向, 且高、低速条带之间是对称的,Q2的上方和Q4的下方存在高剪切层.

图14
图15对比了统计平稳均匀剪切湍流中的Q2 ~ Q4对(图15(a) ~ 图15(d))以及槽道湍流中的壁面分离(图15(b)(e))和壁面附着(图15(c)(f))Q2 ~ Q4对周围的统计平均流场. 其中图15(a) ~图15(c)为位于Q2~Q4对中心zy截面上的平均脉动速度, 图15(d) ~ 图15(f)中蓝色和黄色等值面分别为流向脉动速度和平均涡量场的拟涡能, 当壁面的约束逐渐增强时, 高低速条带之间的不对称越发明显, 在图15(f)中壁面附着Q2 ~ Q4对周围的低速条带很小以至于被拟涡能等值面掩盖. 图15表明, 统计平稳均匀剪切和槽道湍流中Q2 ~ Q4对周围的流场并无本质的差别, 壁面只是为拟序结构提供了可附着的载体. 关于图15的更多细节还可参考Jiménez (2018a).

图15
需要指出的是, 如果单独对Q2或Q4做条件平均, 会分别在Q2的上方和Q4的下方得到发卡涡(Dong 2016), 然而, 正如Robinson (1991)指出, 由于流动在展向的对称性, 无差别的条件平均必然得到对称的发卡涡, 但这似乎并未引起学术圈的广泛重视, Lozano-Durán等(2012)和本文作者的结果(Dong et al. 2017)表明, 对成对的Q2 ~ Q4做条件平均则更能反映流动的真实情况.
Lozano-Durán等(2012)和Dong等(2017)研究的是雷诺应力本身, 然而, 在Navier−Stokes方程中出现的是雷诺应力的散度∂(ui'uj')/∂xj. 对任意一个散度为零的张量Ψ,∂(ui'uj')/∂xj与∂(ui'uj' +Ψij)/∂xj是等价的, 这就导致当地的动量通量不唯一. 据此, Jiménez (2016)提出了最优动量通量(optimal momentum flux)的概念, 他发现最优动量通量与雷诺应力的瞬时场和单点统计特性有较大差别, 因此, 雷诺应力是否能够真实反映动量传递需要进一步研究. 于是, Osawa和Jiménez(2018)从结构的角度进一步比较了雷诺应力和最优动量通量之间的异同. 结果发现最优动量通量结构也可以分为壁面附着和壁面分离两类, 其中前者是自相似的, 且贡献了绝大部分的动量通量. 更重要的是, 最优动量通量周围的平均流场同时包含了上抛和下扫(图16), 这说明雷诺应力本身是可以反映动量通量的, 当然, 应当将上抛和下扫视为同一结构的两个部分, 这与Lozano-Durán等(2012)和Dong等(2017)的观点是一致的.

图16
以上讨论的都是二维剪切湍流(只有一个方向有平均剪切), 而在自然界和工程实际中, 三维(除了流向速度还有横流速度)剪切湍流则更常见, 例如龙卷风、后掠翼边界层、水下航行体表面边界层和叶轮机械内部流动等. Coleman等(2000)指出, 相比于平稳态的三维湍流边界层, 二维湍流边界层受到突发三维效应后的非平稳响应过程具有更大的挑战. 在这里对三维湍流边界层的性质不作过多的介绍, 感兴趣的读者可以参考van den Berg (1975), Bradshaw和Pontikos(1985), Degani等(2013), Coleman等(2000). 但是其中两个与雷诺切应力密切相关的特点需要指出: (1)雷诺切应力不再“跟随”平均剪切, 即这在非平稳三维壁湍流中更明显; (2)雷诺切应力幅值与湍动能之比随着三维效应的增强而减小.
最近, Lozano-Durán等(2019)在Reτ≈ 500和1000的槽道湍流中研究了二维湍流边界层在不同强度的瞬时展向压力梯度影响下雷诺应力随时间的演化规律. 他们对受到突发展向压力梯度之后不同时刻的上抛−下扫对作了条件平均, 随着时间推进, 上抛和下扫的流向长度变小, 而高度维持不变. 在近壁区(图17中白色虚线以下),的区域逐渐增大, 表明近壁流动逐渐散失拟序性. 同时, 高低速条带都有所减弱, 尤其是低速条带.

图17
他们提出了受突发展向压力梯度影响下的条带−流向涡模型(图18(b)). 图18(a)是二维壁湍流中反复提及的条带−流向涡模型. 他们发现条带−流向涡对突发的展向压力梯度的响应过程是自相似的, 即不同尺度的壁面附着流向涡对dP/dz的响应时间与其大小(也即离壁面距离)成正比, 由于近壁面的小尺度结构比远壁面的大尺度结构先受到dP/dz的影响, 近壁面和远壁面流向涡涡轴方向存在偏差, 导致雷诺切应力减弱. 根据该模型, 他们模化的雷诺切应力为

图18
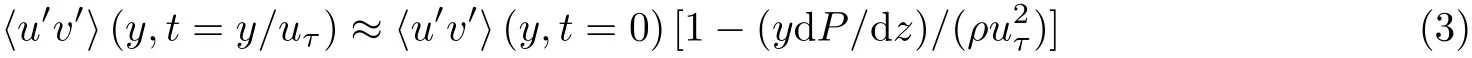
3.3 速度结构
长期以来, 由于低速条带(u' < 0)和发卡涡密切相关, 一直受到较大关注, 而高速条带(u' > 0)受到的关注则少得多. Robinson等(1989)和Robinson (1991)较早注意到了高、低速条带之间的不对称性, 他们认为在近壁区高速条带比低速条带要短, 但是更宽, 并预测高、低速条带之间的差别在高雷诺数时会更明显. 针对高、低速条带的条件相关函数表明(Lee & Sung 2013, Sillero et al. 2014), 只有在脉动较强时(如|u'| >urms), 高、低速条带之间的差别才会显现. 但是这一现象一直没有引起人们的足够重视, 直到采用聚类连通法将高低速条带分开之后, 人们才对高、低速条带有了更加深入的了解.
最早采用聚类连通法研究速度条带可追溯到2004年. Jiménez等(2004)在研究槽道湍流近壁区的大尺度流向速度结构时, 采用二维聚类连通法提取了xz平面上(y+= 16)的流向和法向速度结构. 他们认为流向很长的条带是由多个较短的条带合并而成, 而小尺度的条带则是法向速度对平均剪切的扰动造成的, 且法向速度结构应该分别在新生成的低、高速条带的上游和下游, 他们通过计算法向速度结构与小尺度条带的相对位置证实了这一推断. 当然, 从动力学角度上来说, 小尺度条带不一定代表条带刚生成不久, 也可能代表它们即将消亡. 此外, 他们通过理论模型预测的条带长宽之间的关系与二维结构外接长方形长宽之间的关系是吻合的.
采用聚类连通法研究三维速度结构则是在10年之后, Sillero (2014)首次研究了δ+≈ 2000的零压力梯度平板湍流边界层中的三维条带, 他发现绝大多数条带是壁面附着的(约占总体积的95%), 且几何上是自相似的(Δx≈ 5Δy, Δz≈ Δy). 图19为Sillero (2014) 提取的高速条带, 个别的超大尺度结构达到了(Δx, Δy, Δz) ≈ (25δ,δ, 10δ), 但达到Δy≈δ的低速条带却几乎没有, 高低速条带之间几何上的这种不对称在上文中已经提及(图11(c)(d)).

图19
del Álamo等(2006)最早将Townsend的附着涡假设中壁面附着的概念具体化, 即三维结构离壁面的最小距离ymin+≈ 0. 这些壁面附着的拟序结构(如涡簇、雷诺应力结构、速度结构和最优动量通量结构)满足附着涡的两条性质, 即几何自相似

以及法向分布密度与高度成反比

其中指数γ= −1是附着涡模型的预测值(Perry & Chong 1982). 以上两点虽符合附着涡的几何性质, 但严格意义上不能完全据此认为壁面附着的拟序结构就是附着涡, 因为除了以上两点, 附着涡 内 速 度 脉 动 的 强 度 需 满 足(Townsend 1976, Perry & Abell 1977, Meneveau & Marusic 2013,Yang et al. 2018, Mehrez et al. 2019)

其中p=1, 2, 3, 4. 式(6)表明在固定的y+处

此外, 附着涡中流向速度脉动的预乘谱存在一个平台区(k−1region), 即在一定波数范围内

其中k可以为流向波数kx或展向波数kz. 以上Ap,Bp,Cp,Dp和E均为常数.
人 们 在 高 雷 诺 数 湍 流 中 确 实 观 察 到 了 这 些 统 计 规 律(Hultmark et al. 2012; Marusic et al.2013, 2019;Meneveau & Marusic 2013; Sillero et al. 2013; Lee & Moser 2015; Örlü et al. 2017; Yang et al. 2018), 因此, 学术界对附着涡的存在性已有广泛的共识, 但对附着涡到底是何种具体的拟序结构仍缺少认识. 由于式(6) ~ 式(10)都是关于脉动速度的统计规律, 因此, 直觉上, 三维速度结构可能是寻找附着涡的突破口.
Hwang和Sung (2018)在δ+≈ 1000的零压力梯度平板湍流边界层中提取了流向、法向和展向速度结构, 并首次研究了这些速度结构中脉动速度的统计规律. 图20为他们提取的壁面附着的速度结构, 与v和w结构相比,u结构在流向有更明显的拉伸. 虽然vrms比urms和wrms要小很多, 但由于速度结构是根据各自脉动的均方根提取的(|ui'| > 1.5ui,rms,i= 1, 2, 3), 因此壁面附着的v结构(图20(c))的体积比w结构(图20(b))的还要大是合理的. 需要注意的是u和w是壁面附着的量而v并不是, 这里的壁面附着v结构只是聚类连通法造成的几何上的附着.

图20
壁面附着速度结构的宽与高满足Δz≈ Δy, 高度在550 < Δy+< 750范围内的u结构的长度与高度满足线性关系(Δx≈ 3.8Δy), 而对数区内Δy+< 500的u结构的Δx与Δy是非线性的, 他们认为这是低雷诺数造成的, 并预测如果对数层内所有壁面附着u结构的长度与高度都满足线性关系,Reτ至少为5000. 壁面附着速度结构的法向分布密度ns与它们的高度成反比, 特别是当220 <Δy+<550时,u结构的分布密度ns≈ Δy−1.

Hwang和Sung (2018)并没有区分速度脉动为正、负的速度结构. 一年后, 在Reτ至3000的圆管湍流中, 他们对高速和低速条带分别做统计(Hwang & Sung 2019), 结果表明, 相比低速条带,高速条带中的平均速度剖面更符合对数律(图21). 他们认为高、低速条带间的这一差别可能也是雷诺数不够高导致的. 虽然Reτ= 3000时高速条带中的平均流向速度剖面已存在明显的对数律(图21(b)), 但即使在雷诺数高达Reτ=O(104~ 105)的圆管湍流实验中, 全流场平均速度剖面的对数律指示因子(indicator function)在均值附近仍有较大波动(Hultmark et al. 2012, Örlü et al.2017).
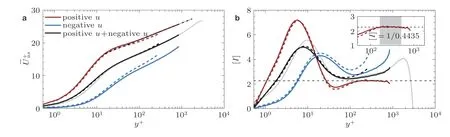
图21
在Reτ≈ 3000的圆管湍流中, 长度和高度满足线性关系(Δx≈ 4Δy)的u结构的高度下限值比δ+≈ 1000的零压力梯度平板湍流边界层中低150δν, 这间接证明了几何自相似性是高雷诺数的特性. 在δ+高达26 000的湍流边界层中, 流向脉动速度的二维能谱表明流向和展向波长满足λx≈λz(Chandra et al. 2017), 而不再是低雷诺数情况下的λz≈λx1/2. 虽然流动的波长和结构的长度并不等价, 但del Alamo等(2006)的结果表明结构的Δx/Δz能大致反映波长之间的关系, 因此, 雷诺数足够高时, 壁面附着u结构的长与高可能将满足线性关系.
后来, 他们采用同样的方法, 研究了逆压梯度平板湍流边界层(δ+≈ 800)中的u结构(Yoon et al.2020), 并按照壁面附着和自相似与否将其分为了四种类型, 即壁面附着/自相似、壁面分离/自相似、壁面附着/非自相似和壁面分离/非自相似. 壁面附着/自相似的u结构法向的分布密度ns在0.4δ< Δy< 0.58δ的高度范围内满足ns≈ Δy−1; 在对数层内, 结构内流向速度脉动的展向波数预乘谱在展向波长为λz+/y+≈ 1.2 ~ 2.0的范围内为常数(即满足式(10)). 壁面附着/非自相似的u结构高度Δy=O(δ), 长度O(3δ~ 6δ), 它们是流向脉动速度在外层峰值的主要贡献者. 壁面分离/自相似的u结构主要出现在外层, 且几何上是各向同性的(Δx≈ Δy≈ Δz), 它们可能是从壁面附着/非自相似结构上脱落下来的. 而壁面分离/非自相似的结构长度为当地的Kolmogrov长度. 对这四种类型流向速度结构的总结详见Yoon等(2020)中表3.

本文作者发现高、低速条带统计特性的不对称并不是Hwang和Sung (2018)声称的低雷诺数引起的. 图22为高、低速条带内的剪切因子S*沿法向的变化. 剪切因子S*=Sq2/ε可以理解为特征长度和速度分别为Lε=q3/ε和q的结构的生存周期q2/ε与平均剪切的特征时间1/S之比.S*>>1表示结构被剪切扭曲变形;S*<<1则表示结构几乎不受剪切的影响, 只有黏性耗散起作用.y/h> 0.02时低速条带中的S*比高速条带中大很多. 因此, 低速条带在高剪切条件下很难保持具有对数律的平衡态.

图22
从Lozano-Durán等(2012)和Dong等(2017)的研究中已经知道高、低速速度条带分别与下扫和上抛事件密切相关, 本文作者通过流向速度结构中平均流向和法向脉动速度的概率密度函数也证明了这一点. 由于下扫事件来自平均剪切较弱的远壁区, 而上抛事件则来自平均剪切较强的近壁区(在下节中将讨论上抛和下扫的运动规律). 因此, 不难理解为什么低速流向条带中的S*比高速流向条带更高, 这也能很好地解释w' > 0和w' < 0两类结构的对称性, 因为w' 对v' 没有偏向所以这两类结构中的剪切常数是相等的.
Hwang和Sung (2018, 2019), Yoon等(2020)和Cheng等(2020a)只考虑了u结构中u' 和w结构中w' 的统计规律, 但是附着涡中三个脉动速度分量应同时分别满足式(6) ~ 式(8). 其实仔细思考会发现, 由于w' 对u' 也没有偏向且w' > 0和w' < 0是对称的,u结构中w' 的脉动强度也应符合对数规律, 虽然暂不清楚与高速条带紧密相关的v' < 0结构中v' 的脉动强度是否存在平台区, 但高速条带应该是目前最符合附着涡性质的拟序结构. 当然, 并不排除其他拟序结构也满足附着涡假设, 但高速条带是最容易获得的一种拟序结构, 这对流动控制具有重要的参考意义.
3.4 其他
最近, 本文作者研究了统计平稳均匀剪切湍流中的亚格子能流结构(Dong et al. 2020). 亚格子能流(sub-grid scale energy flux)

其中波浪线代表滤波.ПSGS> 0代表湍动能从解析尺度向滤波尺度传递, 即正级串(forward cascade); 而ПSGS< 0则代表逆级串(backward cascade). 级串事件周围的统计平均流场表明它们位于强剪切区(图23). 对于正级串, 剪切层是由于上抛和下扫的碰撞引起的; 而对逆级串, 剪切层则是由下扫和上抛的分离导致的.
平均涡量场的拟涡能以正、反发卡涡的形式出现(图24), 正、反发卡涡分别位于级串事件的下游和上游. 发卡涡上平均涡量的方向(图中箭头)取决于亚格子能流的符号. 涡头以展向涡量占主导, 而涡腿则以流向和法向涡量占主导.
实际上, 前人基于二维条件平均对壁湍流中能量级串周围的流场开展过大量的研究, 虽然他们并没有直接得到类似图24中的发卡涡, 但是他们推测能量级串只单独与正或反发卡涡有关(Piomelli et al. 1991, 1996; Porté-Agel et al. 2001, 2002; Hong et al. 2012). 虽 然 反 发 卡 涡 在 槽 道(Kim & Moin 1986)和均匀剪切湍流(Kim & Moin 1987)中均早已被发现, 但在此之前, 还从来没有任何物理现象能将正反发卡涡同时联系起来. 图23和图24中的模型极大简化了人们对能量级串的理解, 同时也表明二维条件平均结果往往存在很大的局限性. 在均匀各向同性湍流中没有上游和下游之分, 因此, 各向同性情况下能量级串周围的统计平均流场仍值得继续研究.

图23

图24
图23中的上抛和下扫在流向是成对出现的, 这与发卡涡串模型(Adrian et al. 2000)是一致的, 但似乎又与Lozano-Durán等(2012)和Dong等(2017)的结果是相违背的. 实际上, 图10和图13给出的是上抛和下扫最可能的空间构成, 并不排除其他可能的、概率较小的空间分布形式, 且图24不涉及三维上抛和下扫之间重心的相对位置.
Dong等(2017)并没有揭示能量级串周围强剪切的来源, 最近, Wang等(2021)在研究槽道湍流中的能量传递现象时, 将式(11)拆开, 分析了对亚格子能流的贡献, 并通过线性随机估计获得了能量级串事件周围的二维平均流场, 他们的结果表明大尺度条带的蜿蜒是造成强剪切和能量级串的原因, 因此, 图24中流向成对的上抛和下扫很大可能也是条带的蜿蜒造成的.
最后, 需要说明的是, 图24中的发卡涡是流动在展向对称条件下条件平均的必然结果, 不代表流场的瞬时特性.
4 拟序结构的动力学过程
Lozano-Durán和Jiménez (2014a)首次采用基于连通域重叠的时空追踪方法研究了槽道湍流(Reτ≈950, 2000和4200)中三维雷诺应力结构和涡簇的时空演化特性, 并从结构合并与破碎的角度揭示了能量级串的规律. Lozano-Durán等(2012)和Lozano-Durán和Jiménez (2014a)一起,构成了对槽道湍流中雷诺切应力结构和涡簇的运动学特征和动力学过程的完整定量刻画.
他们发现壁面分离分支(wall-detached branches, 分支的每一时刻结构都不附着于壁面)的生命周期与其重
心yc处的Kolmogrov时间tη成正比, 而壁面附着分支(wall-attached branches, 分支中至少有一个时刻结构附着于壁面)的生命周期大致为涡翻转时间(eddy-turnover time)ly/uτ(ly为在壁面附着分支整个生命周期内结构的平均高度), 这首次证实了壁面附着结构在时间上的自相似性, 即生命周期正比于结构的大小.
上抛在近壁区生成, 并在其前2/3的生命周期中保持壁面附着状态, 之后快速远离壁面并逐渐消亡; 而下扫则反过来, 它在远壁区生成, 之后逐渐向壁面移动, 在其1/3生命周期之后一直附着于壁面, 直至消亡. 涡簇和上抛的法向轨迹类似, 但是它们在法向的运动距离非常有限. 上抛和下扫的重心在法向的平均运动速度分别为uτ和−uτ. 在流向, 除了近壁区部分(y+< 100), 上抛各xz截面的平均速度为〈u〉(y) − 1.5uτ, 下扫各xz截面的平均速度则为〈u〉(y) + 1.5uτ. 本文作者Dong (2016)对均匀剪切湍流中的上抛和下扫也进行了时空追踪, 并得到了同样的运动速度. 这再次表明壁面对剪切湍流中拟序结构的动力学过程没有本质影响.
此外, 刚生成的上抛(下扫)与已有大尺度壁面附着上抛(下扫)的位置关系表明. 新生成的上抛都在已有上抛的下游, 而新生成的下扫则在已有下扫的上游. 这与上文中上抛(下扫)在流向一连串出现是一致的. 当然, 这里的结果是否反映了大尺度结构对小尺度结构的诱导(即因果关系)还需要进一步研究.
上文提到, 拟序结构在其时空演化过程中不可避免地会与其他结构合并为一个尺度更大的结构, 或者分裂为多个尺度较小的结构. Richardson (1920)和Obukhov (1941)关于能量级串的唯像模型认为湍流中的能量由大尺度向小尺度的传递过程(正级串)是通过类似于细胞分裂的“涡破碎”实现的(一个大小为d的“涡”分裂为两个大小为d/2的“涡”). 据此, Lozano-Durán和Jiménez (2014a)将拟序结构的分裂与合并作为级串事件, 即结构的分裂代表能量从大尺度结构向小尺度结构传递(正级串); 而反之, 几个结构合并为更大尺度结构代表能量从小尺度向大尺度传递(逆级串). 他们发现, 当三维结构外接长方体的对角线长大于100η时会至少发生一次合并或分裂, 正级串(分裂)主要发生在拟序结构生命周期80%的阶段, 而逆级串(合并)则发生在拟序结构生成不久(生命周期的20%), 正级串和逆级串分别主要发生在拟序结构生命周期的后期和前期. 绝大多数的合并与分裂都涉及一个Kolmogrov尺度的“小碎片”(d≈ 30η), 但均衡的能量级串(balanced cascade, 即分裂后或合并前两个结构的尺寸相当), 即类似于Richardson (1920)和Obukhov (1941)提出的级串模型, 在整个惯性区间也都存在. 发生均衡的能量级串的时间间隔与结构的大小成正比. 这是湍流界首次对Richardson (1920)和Obukhov (1941)能量级串模型的定量刻画.
基于Kolmogrov (1941)能量级串(即能量传递发生在尺度间)模型, 人们往往通过滤波后亚格子能流的符号判断能量级串的方向(如Dong et al. 2020). 这与三维结构合并与分裂的角度是完全不同的. 若流场没有被滤波, 那么即使结构的几何尺寸很小, 它们包含的流场实际上也有各种不同尺度(波长)的贡献. 对于亚格子能流, 逆级串与正级串的比值与滤波方法、滤波尺度、离壁面距离和雷诺数等都有关系, 而从拟序结构合并与分裂的角度, 正级串与逆级串的比值则与结构的类型有关, 对于雷诺切应力结构, 正级串和逆级串事件的比例约为1.3, 对于涡簇, 这一比例约为2.2.
后来, Cardesa等(2017)结合滤波和聚类连通域法, 研究了能量在空间(三维)、尺度和时间五个维度中的传递, 弥补了Richardson (1920)和Obukhov (1941)能量级串模型只考虑能量的空间传递而Kolmogrov能量级串模型只考虑能量尺度间传递的缺陷.
与Lozano-Durán和Jiménez (2014a)不同的是, Cardesa等(2017)中的能量级串不再是指三维结构的分裂与合并, 而是指不同滤波尺度下获得的三维结构之间的空间重叠. 如图25所示, 对每一个尺度为A的结构(橙色), 它与尺度为B的结构(蓝色)的相对重合率R(A,B)定义为二者重合的体积除以A本身的体积, 即

图25

他们先用一组滤波尺度Δ/η=30, 60, 120和240, 对Reλ =315的均匀各向同性湍流进行了滤波. 对某一滤波尺度Δ1, 他们采用的带通滤波只保留尺度在范围内的流动信息, 滤波之后的能谱如图26所示.

图26
然后, 他们用聚类连通法获得了不同滤波尺度下的三维含能结构(以湍动能为提取条件,图27). 这时, 所提取的三维结构中只有特定波长的贡献, 因此, 虽然图27(a)中存在几何尺度比图27(b)中还小的结构, 但是其内部的流场却是由更大尺度贡献的.

图27
结果表明(图28(a)), 在含能结构的生存周期内, 只有滤波尺度成两倍关系(如Δ/η= 30和60)的拟序结构之间才有显著的能量交换, 而成其他倍数关系时(如Δ/η= 30和120), 对应结构之间的空间重叠符合零假设(null hypothesis), 即空间重叠是随机的. 更有意思的是, 若将R(A,B)以整个生存周期中的最大值归一化(图28(b)), 以滤波尺度为Δ/η= 60获得的三维结构为例, 它们与滤波尺度为Δ/η= 120的结构发生能量交换(重叠率的极大值)的时间为它们刚生成不久(生存周期的20%); 而反过来, 它们与Δ/η= 30结构的能量交换则发生在它们将要消失之前(生存周期的80%). 也就是说, 小尺度结构刚生成不久需要从大尺度获得能量, 而即将消亡时, 它们将能量传递给更小尺度的结构(需要再次强调的是, 这里的尺度不是指结构的几何尺度).

图28
Cardesa等(2017)首次定量刻画了湍动能在空间和尺度间传递的动力学过程, 极大深化了人们对级串过程的理解.
基于连通域的拟序结构追踪方法的最大优势是它可以实现对任意流场特征的追踪. 例如, 最近Cardesa等(2019)又对槽道湍流(雷诺数Reτ= 950)中的三维回流(backflow, 即瞬时流向速度u< 0)结构进行了时空追踪. 回流结构在时空演化过程中几乎不发生分裂与合并, 因此其性质比Lozano-Durán和Jiménez (2014a)中的雷诺应力和涡簇要简单的多. 它们在流向的运动速度(流向运动的距离除以生存周期)约等于y+= 12处的平均流向速度. 此外, 他们还获得了回流结构在生存周期不同阶段的统计平均流场, 这在类似的研究中是第一次.
Cardesa等(2019)将三维回流结构的生命周期分为了8个等分, 图29为回流结构在其前1/8生命周期内的统计平均涡量场(非脉动量). 图中红色等值面代表展向涡量绿色和蓝色等值面分别代表法向涡量为零. 图中黑色区域为该阶段回流结构的平均外接长方体. 由于回流是非常罕见的现象, 因此, 三维回流结构是一种空间尺度非常小的结构, 平均大小仅为Δx+≈ Δz+≈ 20, Δy+≈ 1, 且与雷诺数无关. 但是得到的平均展向涡量却延伸到回流结构下游近300δν, 据此他们认为这可能是某些近壁统计量采用黏性尺度标度时失效的原因.
图29给出了回流结构整个生命周期的不同阶段在xy截面上(图30中的淡蓝色截面)的统计平均流场, 流场用展向涡量的平均值〈ωz〉无量纲化. 他们还保存了回流结构生成之前(a,b,c)和消亡之后(l,m,n)一段时间内的流场. 在回流结构生成之前, 在y+< 15的整个流向区域,ωz非常低, 他们认为可能这是回流结构出现的前兆. 在a时刻, 出现了流向很长的高剪切层, 随后, 在回流结构所在位置(x= 0)的下游, 高剪切层逐渐切斜, 并与上游的分开, 二者之间有一个明显的弱ωz区, 在回流结构生成的时刻, 强ωz明显向近壁移动. 时刻i之后, 回流上游的剪切层逐渐远离壁面, 同时强度减弱. 回流结构消亡之后, 下游的剪切层也逐渐减弱.

图30
在文章的最后, 表2总结了采用聚类连通法进行湍流拟序结构研究的代表性工作.
5 结 论
本文回顾了人们采用聚类连通法在湍流拟序结构方面取得的重要发现: 剪切湍流中包含了涡簇、上抛和下扫、速度条带、剪切层和准流向涡的拟序结构综合体; 满足附着涡特性的高速条带; 湍动能在空间、尺度和时间五个维度的传递. 这些基于统计方法和拟序结构深度融合的研究成果极大扩展了人们对壁湍流的认识.
经过几十年的研究, 除了外层的超大尺度结构(VLSMs), 湍流界对近壁区和对数区拟序结构的运动学特性已有较深入的认识. 本文的结果表明, 对拟序结构的研究应当从建立包含多种物理现象的拟序结构综合体角度出发. 这为研究存在多物理场耦合效应的湍流场中的拟序结构提供了思路, 例如在可压缩湍流中, 边界层内除了动量传递还有热量传递, 由于温度与速度有较强的关联性, 热量传递应该也可以包含在Lozano-Durán等(2012)和Dong等(2017)建立的拟序结构综合体中.
然而在动力学方面, 除了近壁面, 人们对壁湍流其他区域动力学过程的认识还不够深, 难点主要体现在多尺度之间的相互作用. 高性能计算和实验手段的发展都使得研究时间分辨的高雷诺数湍流逐渐成为现实和未来的趋势. 基于连通域重叠的时空追踪方法被证明是研究湍流动力学过程的有力工具之一, 相比其他方法, 该方法的优势除了可以对任意流动特征进行追踪, 也可以同时对多种结构进行追踪, 以研究它们之间可能的相互作用, 但目前只有少量的工作采用了该方法. 本文作者认为该方法可能会在以下方向取得突破性进展:
(1)VLSMs的生成机制: 人们对VLSMs的生成机制仍存在较大争议(郑晓静和王国华 2020),主要还是因为缺少对VLSMs生成演化过程的定量刻画. 由于VLSMs是高雷诺数下独有的特征,这项工作具有较大的挑战. Jimenéz (2018b)认为VLSMs很可能是较小尺度的结构级联造成的,但是对具体的级联过程还缺少深入认识.
(2)摩阻和热流的生成机制: 壁面摩阻和热流对飞行器的性能至关重要, 它们在时空上具有很强的间歇性, 这必然与壁面附着结构的时空演化有关. 摩阻分解方法从统计平均意义上揭示了摩阻的生成机理以及热流与摩阻的定量关联(Li et al. 2019). 然而, 对强摩阻和热流事件在演化过程中与边界层内拟序结构的联系尚不清楚.
(3)附着涡的时空演化及伴随的尺度间相互作用: 附着涡是有生命周期的, 不同尺度的附着涡之间可能会有相互作用. 前人对这一问题几乎没有开展研究, 很大程度上是因为附着涡一直处于抽象的统计概念之中, 而最近人们已将其与高速条带联系起来, 并且还有可能发现其他符合附着涡特点的拟序结构.
(4)湍流中的因果关系和预测: 理解湍流中不同现象间的因果关系(例如Lozano-Durán et al.2020)并实现对湍流的预测和控制具有十分重要的意义, 例如, Jimenéz (2013a, 2013b, 2015)和Encinar & Jimenéz (2020)从猝发过程中速度脉动倾斜角的规律提出了猝发的预测方法. 此外, 拟序结构的生成演化与人工智能结合的角度也会是个突破口(Jimenéz 2018b, 2020).
致 谢 董思卫感谢Jimenéz教授在写作过程中给予的热情帮助. 国家自然科学基金(11702307,12072306), 国家重点研发计划(2016YFA0401200, 2019YFA0405200)以及国家数值风洞(NNW)资助项目.

