电磁霍普金森杆实验技术及研究进展

王维斌 索 涛 郭亚洲 李玉龙 聂海亮 刘会芳 金康华 杜 冰 江 斌西北工业大学航空学院, 西安 710072

陕西省冲击动力学及工程应用重点实验室, 西安 710072冲击动力学及其工程应用国际联合研究中心, 西安 710072

1 引 言

传统霍普金森杆实验装置的研究起源于20世纪初期(Hopkinson 1914), 最初的霍普金森杆只能测量冲击载荷下的脉冲波形. Davies (1948)在Hopkinson设计的装置基础上发明了利用电容方法测量杆中的应力脉冲. Kolsky (1949)将霍普金森压杆采用入射杆、透射杆分离式结构用于研究材料在高应变率下的动态力学行为及材料的动态本构关系, 成功发展了分离式霍普金森压杆(图1), 简称SHPB (split Hopkinson pressure bar), 很多学者利用该实验装置开展了大量的材料动态性能研究工作.

图1

由于材料与结构的动态变形及破坏过程都是在应力波的作用下发生的, 因此应力波的产生方式至关重要. Kolsky (1949)设计的实验装置最初是利用炸药起爆来产生冲击脉冲, Krafft等(1954)改用炮/枪发射一个弹体(通常称为撞击杆)撞击入射杆形成了一个梯形脉冲, Hauser等(1961)使用Hyge速度发生器成功获取了恒定幅值的应力波. 1964年, Lindholm进一步完善了霍普金森压杆装置, 后来的研究者所使用的霍普金森杆基本上都是通过高压气体驱动子弹撞击入射杆来产生入射波.

将预先储存的弹性势能突然释放是应力波的另一种产生方式, 其中部分入射杆被静态扭转、拉伸或压缩而夹紧并施加预应力(Duffy et al. 1971), 该方法虽然可以同时释放拉伸(或压缩)波和扭转波, 但由于应力波纵波与横波速度不同, 应力波到达同一试样的时间存在差异, 因此试样未能同时完成加载.

除子弹撞击与能量释放两种方式外, 也有研究学者考虑将电磁驱动技术应用到霍普金森杆实验技术中. 电磁驱动的原理是将电磁能转换为其他形式能, 目前在电磁成型(Davies et al. 1970)、电磁弹射(Bushway 2001)、电磁轨道炮(李军等 2014)、电磁刹车(牛润新等 2006)、电磁式斜波驱动(Wang et al. 2016)及电磁铆接(Deng et al. 2013)等领域取得了很多突出成果. 赵志衡等(2016)将电磁铆接技术产生的应力波应用于落锤实验中, 以提高落锤实验中的应力水平, 并通过数值模拟与实验结果进行了对比验证, 然而他们仅将该想法应用于落锤实验, 并未扩展到材料动态力学测试的其他实验中.

Silva等(2009)首次提出采用电磁力代替高压气体, 为分离式霍普金森压杆系统中子弹提供驱动力. 郭伟国等(2010)也研制出一套基于电磁驱动技术的微型霍普金森杆实验装置, 并测试了镁合金的动态应力−应变曲线, 验证了装置的可靠性与实用性. 刘战伟等(2013)和Liu等(2014)研制出多级电磁驱动的微型霍普金森杆(图2), 并进行了铝合金材料的动态压缩实验. Huang等(2017)研制的七级磁阻小型化霍普金森杆电磁发射装置具有精度高、体积小、噪声污染小等特点, 符合小型化霍普金森杆对高应变率的要求. Huang等(2019)还研制出一套小型多脉冲串联磁阻线圈发射装置, 其中串联磁阻线圈发射极由两个单级磁阻线圈和两个弹丸组成, 通过电磁驱动两个弹丸依次撞击入射杆产生两个振幅相同的加载脉冲, 这种精确的多脉冲加载技术可用于测量和研究SHPB实验中不同材料的动态响应(图3). 谢倍欣等(2019)和Xie等(2019)研制的双子弹电磁驱动SHPB系统, 使用聚碳酸酯作为杆件材料, 克服了软材料试件带来难以应用于非铁磁材料的问题, 同时实现了对线圈发射的精准控制. Chen等(2014)设计了一套动态压缩与拉伸试验于一体的微型霍普金森杆装置, 电磁驱动技术的引入使得装置结构更加小型化, 且可靠性高,移动方便(图4). 上述学者通过电磁驱动技术对子弹施加驱动力进行材料动态性能的研究, 但其应力波加载方式依然是通过子弹撞击入射杆实现, 相对于更加成熟的气体驱动方式而言, 影响因素更多, 例如子弹上的线圈对入射杆中波形的影响、实验中的电磁干扰问题等.

图2

图3

图4

李玉龙等 (2014a)利用电磁驱动技术研制了一套E-Hopkinson杆多轴动态实验装置, 与电磁驱动子弹方式不同, 该装置由电磁感应产生的电磁力直接对入射杆进行加载, 本质上改变了应力波的产生方式. 在研究多向冲击载荷作用下的材料动态力学性能时, 这些冲击载荷作用时间的同步性必须要保证, 此时传统的霍普金森杆实验技术已很难满足多向冲击载荷作用时间的同步性,E-Hopkinson杆实验技术由于多组电容同步放电时电磁效应在试件上产生的应力与直接施加在试件上的应力时差完全同步, 保证了作用于试件材料上的各向冲击载荷的同步性. 因而可实现复合冲击载荷加载条件下的材料动态力学性能测试. 目前E-Hopkinson杆实验技术已实现试样的单轴双向同步加载与双轴四向同步加载, 本文将侧重于该实验技术的基本原理及在不同领域的一些研究进展进行综合评述, 并对E-Hopkinson杆技术在其他领域中值得继续探索的方向做一展望.

2 E-Hopkinson杆实验技术

2.1 基于电磁能量转化原理的E-Hopkinson杆实验装置

实际上, 应用电磁能量转化原理直接产生应力波的技术早已发展成熟, 但一直未应用于实验力学领域. 电磁能量转换原理早在20世纪60年代就被学者提出, 主要应用在电磁铆接技术领域(Deng et al. 2009), 电磁铆接技术只关注铆钉所产生的变形效果, 很少有对电磁铆枪所产生的应力波特征进行研究. 理论上, 如果将铆钉替换为分离式霍普金森压杆, 电磁铆枪所产生的应力波会通过放大器传入压杆系统, 成为霍普金森压杆实验的入射波, 对试样进行加载. 李玉龙等(2014b)对电磁铆枪中线圈结构进行了优化, 采用铜质锥形次级线圈代替了电磁铆枪结构中的次级线圈和应力波放大器, 减小应力波的脉宽, 同时结合电磁加载系统与加载杆研制了首套单轴EHopkinson杆实验装置(图5).

图5

2.2 E-Hopkinson杆应力波放电电路分析

E-Hopkinson杆实验装置包括充电电路、放电电路及压杆系统, 其中充电与放电电路的设计是E-Hopkinson杆实验装置中非常重要的一个环节. 具体来讲, 首先利用变压器对交流电进行升压, 升压后交流电在经过整流电路后直接对电容进行充电完成储能过程, 最后通过触发高频电子开关控制电容放电, 放电瞬间电容存储的电场能转换为放电线圈中的磁场能, 放电线圈与次级线圈在电磁感应的作用下产生电磁力传递到入射杆中完成应力波的加载. 放电电路通过RLC电路零输入响应来进行暂态分析(谢祖荣等 2002), 其等效电路如图6所示, 图中R为放电回路总电阻、K为放电回路开关、L为放电线圈等效电感, 该电路为典型RLC二阶电路.

图6

放电线圈与次级线圈的结构关系如图7(a)所示, 为简化电路模型, 将N匝放电线圈简化为单匝线圈, 简化后通过线圈电流为单匝线圈的N倍, 即

E-Hopkinson杆应力波发生装置中次级线圈为一铜板, 可将其等效为单匝电流环, 放电线圈与次级线圈的简化模型如图7(b)所示.

图7

由式(1)可推导出次级线圈中感应涡流i2(t)

E-Hopkinson杆应力波发生装置中放电线圈与次级线圈属于共轴线圈, 其放电线圈与次级线圈之间的电磁斥力F与放电电流i(t)关系可表示为(Takatsu et al. 1988)

入射杆中的应力

式中r0为 线圈导向轴半径,r2为 次级线圈半径,µ0为 真空磁导率,ω为放电回路振荡频率,α为放电线圈与次级线圈间距,S为入射杆横截面积.

式(4)中应力σ(t)幅 值主要由互感M、匝数N、间距α、 电阻R、 电感L及放电电流幅值决定.对于已加工成型的应力波发生装置其互感、匝数、电感等参数较难实现动态调节, 而放电电流幅值受电容充电电压影响, 因而应力波幅值可通过调整充电电压实现精确控制.

E-Hopkinson杆实验中应力波的加载在放电电流第一个半波周期内完成, 根据RLC电路放电周期

式中T0为 应力波脉宽,T为放电电流周期. 从式(5)可以看出应力波脉宽受电容C、电阻R和电感L的影响, 对于结构固定的应力波发生装置主要通过调整电容容量来控制应力波脉宽.

2.3 E-Hopkinson杆与传统霍普金森杆装置的对比

E-Hopkinson杆实验技术的发展弥补了传统霍普金森杆实验技术上的一些不足, 促进了材料动态加载技术的发展, 现将两种实验技术进行对比, 希望为E-Hopkinson杆实验技术的发展和改进 提供更多的参考意见.

2.3.1 应力波加载方式

E-Hopkinson杆实验技术与传统霍普金森杆相比, 应力波加载方式有着本质的区别. E-Hopkinson杆实验技术采用电磁驱动技术由次级线圈对入射杆直接进行应力波的加载, 而传统霍普金 森杆大多采用压缩气体驱动子弹撞击入射杆的方式进行应力波加载.

2.3.2 应力波脉宽与幅值调节

E-Hopkinson杆实验技术中应力波脉宽与幅值受电磁加载系统中电路参数的影响, 改变电容容量可调节应力波脉宽, 控制电容充电电压可实现不同幅值的应力波. 目前E-Hopkinson杆实验技术可实现脉宽200 ~ 1100 μs的应力波, 理论上改变电容容量还可实现200 μs以下及1100 μs以上脉宽的应力波, 因此E-Hopkinson杆实验技术未来还可以在中应变率及高应变率下的动态加载领域展开研究. 传统霍普金森杆实验技术中应力波脉宽受限于子弹的长度, 幅值取决于气压的高低, 由于气枪气压的限制, 对于应变率跨度过大的实验需要更换撞击杆的长度来得到不同的应变率, 应变率越高, 所需要的撞击杆越短, 实验中产生的应力波脉宽也越窄, 这就限制了动态实验 的应变范围, 且操作繁琐.

2.3.3 应力波波形

E-Hopkinson杆实验技术中应力波是基于电磁驱动技术产生的, 即在电磁感应定律中交变的磁场感应出交变的电磁力, 由于RLC电路中电容放电电流波形接近半正弦波, 因而加载杆中应力波也呈半正弦波形, 对于脆性材料与软材料测试具有显著的优势. 根据傅里叶变换原理, 通过改变放电线圈中的放电电流形状, 还可进行入射杆中应力波形的优化, 传统霍普金森杆实验技术中 子弹撞击产生的应力波为梯形波.

2.3.4 多轴对称加载同步性问题

E-Hopkinson杆实验技术中, 从放电开关的吸合到应力波的产生几乎无时间延迟, 这是由于脉冲电流在放电线圈中传播速度远大于固体应力波的传播速度, 可以认为电磁感应在试件上产生的应力与直接施加在试件上的应力时差是完全同步的, 因而将两个参数一致的放电线圈并联,由同一电容放电, 两放电线圈与各自对应的感应线圈上将同时产生幅值脉宽相同的应力波, 所述应力波同时输入对称加载装置的两个入射杆中, 同时到达试样两个端面, 实现对试样对称加载.通过对E-Hopkinson杆实验装置的改造及电磁加载系统的优化可实现双轴四向、三轴六向的对称加载, 传统霍普金森杆通过子弹撞击入射杆机械撞击的方式来实现对称加载几乎是不可能的,且现有的多轴动态实验技术大多是基于拉剪或压剪实验.

3 E-Hopkinson杆实验技术应用

E-Hopkinson杆实验技术于2015年由本文作者团队首次提出, 对于完善与拓展材料动态力学 行为的研究具有重要意义, 目前已经在多个领域得到应用.

3.1 单轴单向E-Hopkinson杆实验技术研究

Nie等(2018a)首先开始了对单轴单向E-Hopkinson杆实验技术的研究, 针对电容放电时脉冲磁场产生机理进行了理论推导与分析. 图8为有限元分析软件ANSYS中的多物理场耦合工具进行电磁场模型的网络划分, 放电线圈置于空气场中以使模拟环境更接近实际实验环境. RLC电路中的链圈元件与空气场中的放电线圈上所有节点进行电路自由度的耦合, 从而由链圈元件来等效放电线圈模型.

图8

次级线圈与入射杆结构场模型的部分单元如图9所示, 通过编程将电磁场中次级线圈每个节点的模拟结果作为结构场中的对应节点的初始加载条件导入结构场, 完成电磁场与结构场的间接耦合. 在应力波的传播过程中, 整个结构并无部件的刚体位移及宏观的结构变化, 因此这种间接耦合的方式可以得到较为准确的模拟结果. 通过2 mF与4 mF电容在500 V及1kV电压下的数值模拟和实验测试结果对比(图10), 验证了E-Hopkinson杆实验技术的可行性, 也证实了EHopkinson杆中应力波脉宽与幅值分别受电容容量和充电电压的影响.

图9

图10

图11为2 mF电容在1 kV放电时的数值模拟结果, 从磁场强度分布(图11(a))可以观察到磁场集中分布在次级线圈靠近放电线圈的一端, 磁场在次级线圈表面的方向基本上沿次级线圈的径向. 作用在次级线圈的磁场力分布如图11(b)所示, 磁场力沿次级线圈的轴向分量占主要部分, 而径向分量非常微弱. 磁场力轴向分量在次级线圈上分布并不均匀, 最大分量分布在靠近次级线圈外边沿的地方. 次级线圈感应出的涡流集中分布在次级线圈靠近放电线圈的底面上, 因此电磁力幅值沿着底面向顶面方向迅速衰减. 由于洛伦兹力主要作用在次级线圈靠近放电线圈的底端, 在此端面将直接产生一个应力波, 该应力波在次级线圈锥面与底面之间来回反射多次后被叠加放大, 最后从次级线圈的顶端传入压杆. 以2 mF电容在1 kV电压放电时次级线圈端面与压杆中的应力波为例(图12), 压杆中的应力波幅值远高于次级线圈底端的应力波幅值, 波长也大于次级线圈底端的波长, 这正是应力波在次级线圈中来回反射叠加的结果.

图11

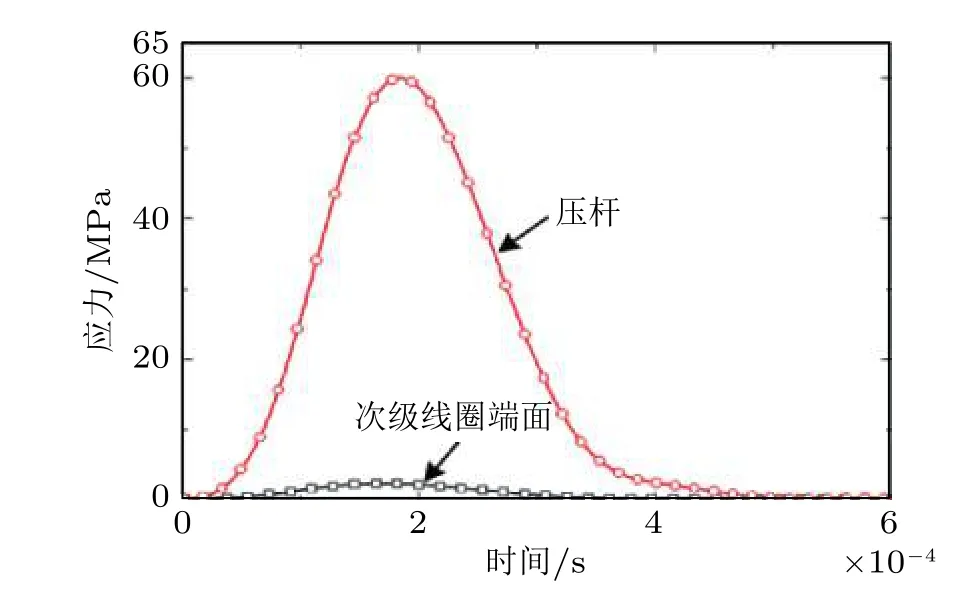
图12

本文作者利用单轴单向E-Hopkinson杆实验装置对黄铜和2024铝合金试样分别进行了动态压缩与动态拉伸实验. E-Hopkinson 杆的动态压缩与拉伸实验结果与传统霍普金森杆实验结果对比 如图13、图14所示, 可以观察到E-Hopkinson杆与传统霍普金森杆实验结果吻合较好.

图13

图14

3.2 单轴双向E-Hopkinson杆及其典型应用

利用E-Hopkinson杆放电同步性可控精度高的优点, 将两组应力波发生装置中放电线圈采用并联形式, 试样置于相同的两入射杆中间, 控制电容同步放电即可实现对试样的单轴双向动态加载. 单轴双向E-Hopkinson杆压缩加载装置(图15)中两根压杆长度相同, 同步放电时两列入射波可同时到达试样, 对试样进行对称加载.

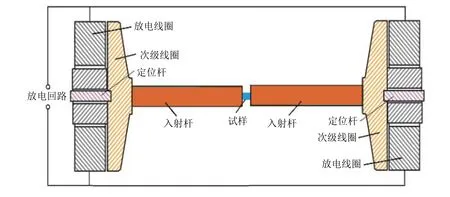
图15

单轴单向E-Hopkinson杆实验的数据处理与传统霍普金森杆实验类似, 但单轴双向加载实验时需要在实验数据处理上进行相应的调整. 单轴双向E-Hopkinson杆压缩实验中传统的透射杆成为另一根入射杆, 左侧入射波和右侧入射波分别同时从两根相同的入射杆端面输入(图16),以图中左侧的入射杆为例, 右行入射波达到界面1时, 一部分波被反射为左行的拉伸波, 另一部分通过试样进入右侧的入射杆; 对于右侧的入射杆, 应力波的传播过程左侧入射波类似. 值得注意的是, 左侧入射杆中形成反射波的同时与右侧入射杆经过试样传来的透射波叠加(忽略波在试样中传播的时间), 这里我们定义两列波叠加后左侧的反射波为左侧反射波. 同理, 右侧入射杆中的反射波也由两部分构成, 称之为右侧反射波.

图16

在进行动态双向加载实验时, 假设试样内部处于应力均匀状态, 试样内部的应力可以表示为试样两端面的应力平均值, 则此时应变、应变率、应力的公式可修改为(Nie et al. 2018b)

式(6) ~ 式(8)中C0为 杆中弹性波速;Sb为 杆中弹性波速;Eb为 杆中杨氏模量;Ls为试样测试端长度;Ss为试样测试端横截面积.

理想情况下两列入射波完全对称, 则有

此时式(6) ~ 式(8)可简化为

式(6) ~ 式(8)适用于对称加载实验一般情况, 式(10) ~ 式(12)适用于两列入射波完全对称的情况. 需要注意的是两套应力波发生器的放电线圈必须精确加工以保证电感量足够相近, 此外两个次级线圈及两根入射杆也必须保证相同的几何参数, 以保证两列入射波的一致性.

江斌等 (2020)利用单轴双向E-Hopkinson杆实验装置对钠钙硅酸盐玻璃进行了动态力学性能测试, 准静态压缩实验在电子万能试验机上进行, 动态单向与动态双向压缩实验均在E-Hopkinson杆实验装置上完成. 图17(a)所示为动态单向压缩实验的原始波形, 图中入射波本身具有一个近似线性上升沿, 无需使用整形技术即可使试样以近似恒定的应变率变形; 图17(b)所示为动态单向压缩实验时试样应力、应变率及应力平衡系数R(t)-时间曲线, 图中试样加载至125 μs后进入应力平衡状态, 并且在约100 μs后实现近似恒应变率加载, 此时应变率约为300 s−1.图18(a)所示为动态双向压缩实验的原始波形, 图中两列应力波除峰值存在微小差异外几乎同时到达试样, 脆性材料一般在入射波上升沿时间段试样就已破坏, 因此峰值差异对实验影响不大;图18(b)所示为动态双向压缩实验时试样两端应力、应变率及应力平衡系数R(t)-时间曲线, 图中试样加载至30 μs后达到应力平衡状态, 约80 μs后达到近似恒应变率加载, 此时应变率约300 s−1.

图17

图18

与动态单向压缩实验相比, 动态双向压缩实验能够使玻璃试样更快地实现应力平衡和恒应变率变形, 从而获得更为精确有效的动态力学性能数据. 此外, 两列相同的应力波对试样进行对称加载, 可大幅减少应力平衡所需时间, 通过实验与数值分析, 对称加载中试样达到应力均匀状态的时间为传统霍普金森杆加载时间的1/3.

除了对称压缩实验, 单轴双向E-Hopkinson杆实验装置还可实现对称拉伸实验, 动态对称拉伸数据处理过程与对称压缩基本一致. Liu等(2018)利用单轴双向E-Hopkinson杆实验装置对碳纤维/环氧树脂复合材料T700/MTM28-1层合板进行了层间断裂特性的研究. 动态断裂实验需要选取可靠的动态加载形式、准确的实验测量手段以及严谨的数据分析方法. 层间断裂韧性的测量采用的试样类型为梁试样, 通过组合梁加载得到不同复合度的层间断裂. 在准静态方面, 已有学者利用双向加载产生不同复合度的层间断裂(图19), 试验机有两套液压驱动装置以及两个力传感器, 通过控制不同比例的拉伸或者压缩位移即可实现不同复合度的层间断裂(Chaves et al.2014). 动态断裂实验方面, 由于传统霍普金森杆装置利用子弹撞击产生应力波, 以刚体碰撞的方式产生两列同步应力脉冲是不可能的, 子弹的速度与撞击无法精确的控制很容易出现应力波加载时的不同步现象, 继而出现断裂类型不再为纯I型断裂. 利用单轴双向E-Hopkinson杆加载装置对双悬臂梁试样进行对称加载, 保证了试样从起始到扩展过程均为纯I型动态断裂, 成功解决了复合型动态断裂的实验难题.

图19

由高速摄像机拍摄的DCB试样对称加载与单边加载变形过程对比可知(图20), 对称加载过程中试样的中心线几乎保持不变, 而单边加载试样的中心线在加载过程中由于加载力的不对称性而产生偏移, 整个试样出现倾斜, 这种变形的不对称性将引入II型动态层间断裂.

图20

图21(a)为一次对称加载实验数据经过移波后的入射波和反射波, 可以观察到加载杆1与加载杆2上应力波的起始点存在微小差异, 加载杆1早于加载杆2约 10us, 而两加载杆上应力波的下降沿完全一致, 分析可能是由于入射杆杆端的法兰与次级线圈的接触不良导致. 图21(b)为试样对称加载过程中I型和II型能量释放率的变化曲线, 图中可以看出II型能量释放率几乎为0, 这也印证了对称动态加载能够保证纯I型的动态断裂.

图21

3.3 金属动态包辛格效应

包辛格效应是指金属材料屈服强度受材料变形历史影响的特性(Bauschinger 1881). 众所周知, 大多数金属都有应变率效应, 这与位错运动及其他障碍的相互作用有关(Hidayetoglu et al.1985). 此外, 材料的包辛格效应可能会受到加载速率的影响(Moan et al. 1979). 准静态包辛格效应试验可以用标准装置进行, Thakur等(1996)采用传统霍普金森杆先对材料进行单次拉伸加载至一定塑性, 再截取试样的部分标距段进行单次压缩加载得到了材料的动态包辛格效应响应, 但该方法由于实验过程复杂且不连续, 难以记录连续冲击过程中热的影响. 单轴双向E-Hopkinson杆实验技术具有较好的同步性与可控性, 可以很好地解决这一问题. 图22所示为利用E-Hopkinson 杆实验技术设计的动态单轴双向非同步加载实验装置, 此装置可用来测定材料在高应变率下的包辛格效应.

图22

实验装置包括两套应力波发生装置、E-Hopkinson杆加载系统、波导杆、数据采集系统等.装置特点在于两套应力波发生装置分别产生压缩波与拉伸波, 两套应力波发生装置由于放电参数完全相同因而保证了波形的一致性. 利用一维应力波理论, 计算并设计两根波导杆的长度使试样能够先后受到压缩波与拉伸波的非同步加载, 从而完成对材料动态包辛格效应的测试. 图23(a)为压缩−拉伸动态循环试验的入射压缩波与拉伸波, 图23(b)表明这两列波一致性较好. 图24是6061铝合金的预压缩−拉伸试验结果, 实验的平均应变率为350 s−1, 压缩最大流动应力为390 MPa,反向加载时拉伸屈服应力为253 MPa, 试样在反向拉伸加载过程中屈服应力下降明显, 说明该材料具有明显的包辛格效应.

图23

图24

3.4 动态双轴冲击实验

考虑到大部分结构实际中所受的载荷通常为多轴复杂应力, 因此研究材料在多轴应力状态下的力学性能对于实际工程应用更具有指导意义. 为实现多轴动态实验国内外很多学者研制了多种加载装置, 现有的多轴动态实验技术大多是拉剪或压剪实验, 且主要基于落锤实验、直接撞击实验及高速飞片冲击实验等. 由于加载设备的限制, 现有的压剪复合加载都是利用单轴霍普金森压杆对特殊设计的试样进行加载, 使试样局部承受压剪复合载荷, 或者对霍普金森压杆加以改造, 以实现压剪复合加载(Rittle et al. 2002). 对于传统气炮式加载方式的霍普金森杆装置, 其双向加载时气炮难以将同步时间精度控制在微秒量级, E-Hopkinson杆实验技术由于电磁感应在试件上产生的应力与直接施加在试件上的应力时差完全同步, 因而通过单轴向双轴的扩展还可实现对试样的动态双轴加载. 图25、图26分别为动态双轴实验装置布局图与实验装置实物图.

图25

图26

图27为动态双轴实验装置双轴四向同步加载时, 黏贴在四根入射杆的应变片采集到的应力波信号, 从图中可以观察到四列应力波信号同步性基本一致.

图27

E-Hopkinson杆动态双轴加载实验的另一个难点是试样的设计, 多轴加载时试样可以是扁平的十字型, 也可以是用于膨胀实验的圆管型, 十字型试样的设计问题是限制十字型双轴拉伸试验的主要难题(Yu et al. 2002). 为了得到完整的应力−应变曲线, 试样的中央区域必须经历弹性变形与塑性变形, 因此在试样设计过程中, 最重要的是使试样大部分变形发生在中央测试区, 避免其他区域出现过于严重的应力集中(Demmerle et al. 1993). 图28为十字型试样的夹持臂经常出现断裂失效而提出了三种解决方案: 切除部分区域、减小测试区厚度、试样臂上加工狭缝. 在试样臂交叉处切去弧形区域能减小此处应力集中, 并增大中央测试区的变形, 而测试区的厚度减薄直接减小了测试区横截面积, 有效地增大了该区域的应变, 狭槽的引入则能减小加载过程中试样臂对试样上载荷分布的影响.

图28

尽管十字型试样广泛用于实验研究, 但一直未有标准的几何形状(Lin et al. 1993). 缺少试样标准, 使得不同实验人员得到的结果难以相互比较. 目前对于十字型试样的相关理论仍未十分成熟, 但对于本文作者团队在双轴电磁杆试样的优化设计具有重大指导意义.

4 结 论

E-Hopkinson杆实验技术利用了电场能转换磁场能的方式来产生应力波, 这是对传统霍普金森杆中应力波加载技术的创新与扩展. 近几年来本文作者团队针对E-Hopkinson杆实验技术开展了大量工作并取得了一定的成果, 对于未来进一步可探究的问题, 其相关研究仍处于起步或者探究阶段. 本文综述了E-Hopkinson杆实验技术在单轴单向及动态双轴对称压缩/拉伸、复合材料的层间断裂、金属动态包辛格效应等领域的应用现状, 涵盖了实验研究, 理论分析及实验结构与有限元仿真的对比. 通过相关文献调研, 针对E-Hopkinson杆实验技术的研究, 本文作者认为未来可在以下方面开展工作.

4.1 应力波整形

目前E-Hopkinson杆实验装置产生的应力波为半正弦波形, 对于脆性材料来说, 可以使材料发生近似恒应变率变形, 但对金属材料来说需要梯形应力波来实现恒应变率加载, 这就需要对应力波进行整形. 如前所述, E-Hopkinson杆实验装置产生的应力波脉宽与幅值与放电回路中电气元件参数有关, 通过对E-Hopkinson杆加载系统中放电电路进行优化, 将原来的RLC电路调整为多级RLC链式电路. 根据傅里叶变换, 任意形状的波形都可分解为若干个正弦波的时序叠加(Yu et al. 2009), 通过高频电子开关控制链式电路中各RLC电路依次放电, 使依次放电产生的应力波相互叠加, 最终加载到入射杆中的应力波即为所需要的波形.

4.2 同步加载及拉扭/压扭多种应力波同步加载

按介质受力状态应力波可分为拉伸波、压缩波、扭转波、弯曲波等, 对试样进行压缩波与扭转波同步加载时材料动态力学性能的测量目前未有文献报道. 考虑到扭转波与压缩波在杆中的传播速度存在差异, 首先计算出两列波到达试样端面的时间差, 然后控制扭转波优先在杆中传播, 通过高频电子开关控制电容放电回路对压缩波释放时间进行延迟触发, 实现扭转波与压缩波同时到达试样, 该方法同样适用于拉伸−扭转等加载实验.

4.3 动态三轴冲击实验

在岩土、混凝土研究领域中, 其三轴受压力学性能是进行结构设计与分析的重要依据. 国外很多研究机构都自行研制了三轴试验装置, 完成了大量的混凝土多轴受压试验研究, 建立了多种强度破坏准则(Park et al. 2005). 国内清华大学研制成功了首台真三轴压−拉试验装置, 随后相继完成了混凝土在各种压拉应力组合下的双轴与三轴力学性能试验(王传志等1987), 大连理工大学也拥有了自主设计制造的三轴试验装置(宋玉普和赵国藩 1990, 1994). 受实验装置的限制, 按应力路径加载的试验很多, 而按应变或应力应变复合路径加载的试验还比较少, 目前还未有文献报道在岩土和混凝土研究领域进行高应变率下三轴同步动态加载实验. 本文作者团队与深圳大学谢和平院士团队正合作研制适用于三维岩石动力学测试的E-Hopkinson杆实验装置(Xie et al.2020), 三轴动态实验装置的布局与双轴试验装置相比需要六套应力波发生装置及六根加载杆进行组装, 图29所示为三轴动态加载装置构想图, 该实验装置可实现对岩石的多种动态加载方式(单轴、双轴与三轴同步), 从而研究岩石在受到冲击扰动下的力学行为, 损伤演化、断裂形态及破坏机理.

图29

4.4 中应变率下动态实验

传统霍普金森杆一般适用于高应变率范围(102~ 104s−1)内的力学性能测试实验, 应变率范围在(10 ~ 102s−1)为中应变率, 此时建立材料本构关系时就需要开始考虑惯性力与应变率对材料性能的影响. 比如战术导弹固体火箭发动机低温点火时, 推进剂面临低温与中应变率(1 ~ 100 s−1)的双重作用(Jeremic 1999); 中应变率加载条件下, 饱水砂岩动态强度与风干砂岩的动态强度相近(王斌等 2010), 因此研究材料在中应变率下的力学特性测试具有重要的工程研究意义. 中应变率实验的难点在于受应力波脉宽的限制, 在一定应变条件下, 降低应变率意味着增大应力波脉宽, 这就需要大幅拉长子弹的长度, 对于传统霍普金森杆实验装置不太现实. E-Hopkinson杆实验装置无需考虑子弹长度, 应力波脉宽取决于E-Hopkinson杆实验装置中电路参数的调整, 增大电容容量的同时调整电容充电电压即可满足中应变率范围内应力波脉宽与幅值要求. 目前E-Hopkinson杆在中应变率领域的研究还处于数值仿真与理论分析阶段, 一旦实现对试样的中应变率实验, 将意味着中应变率研究领域的新突破.

4.5 应力波发生装置中放电线圈与次级线圈的结构优化设计

应力波发生装置中放电线圈结构为铜带缠绕成的扁平状环形线圈, 次级线圈为黄铜或紫铜加工成中心带孔的圆盘状, 放电线圈与次级线圈由电磁感应定律在放电时可产生电磁力. 电磁加载中设计充电电压最高幅值3 kV, 最高脉冲电流幅值达到20 kA, 现有的放电回路虽然满足其放电瞬间的电压幅值与电流幅值, 但电容放电时除了用于感应电磁力需要的磁场区域外, 放电瞬间其空间中存在大量的漏磁场, 漏磁场不仅未得到有效利用, 且对信号采集电路产生电磁干扰, 因此对于应力波发生装置还需要结构上的优化, 在不降低电磁力幅值的条件下改变放电线圈与次级线圈的结构, 目的在于将放电瞬间放电线圈产生的磁场可以大部分集中在线圈附近, 这样不仅提高了电磁能转换为机械能的效率, 还降低电容充电电压与放电电流幅值, 对于高电压大电流的硬件电路也将降低其设计难度.

4.6 抑制E-Hopkinson杆实验技术中电磁干扰

E-Hopkinson杆实验技术中应变信号的测量普遍采用电阻应变片法, 这就需要考虑信号采集电路中电磁效应所带来的电磁干扰. 一方面瞬态磁场在空间以辐射方式耦合到应变片信号采集回路中, 造成电磁辐射干扰; 另一方面数据采集回路与电容放电回路共地, 接地不可靠或未接地都会对应变片采样电路产生电磁传导干扰. 当电容取4 mF及更大容量时, 由于应力波脉宽增大导致电磁干扰信号与采样信号出现信号耦合现象, 从而对应变信号带来干扰, 因此从实验技术及实验效果来讲是必须要解决的重要问题.

致 谢 高等学校创新引智计划资助(BP0719007); 国家自然科学基金资助项目(11527803,11922211, 12172304, 12025205).