双馈电机直接功率控制方法比较及实验研究

蒋 涛，张永昌，徐东林，焦 健，王占扩，张晟铵

（1.华北电力大学电气与电子工程学院，北京 100096；2.北方工业大学电力电子与电气传动北京市工程研究中心，北京 100144）

直接转矩控制DTC（direct torque control）以其原理简单和动态响应快等优点早在20 世纪80 年代就被提出并应用于异步电机驱动系统[1]。1998 年，日本学者进一步将类似的思想用于三相脉冲宽度调制PWM（pulse width modulation）整流器的功率控制，称之为直接功率控制DPC（direct power control）[2]。2000年以后，DPC 和DTC 被相继用于双馈电机风力发电系统来实现有功和无功[3-4]、转矩和磁链[5]的直接控制，目前已经成为双馈电机实现并网发电控制的代表性方法。

传统查表法的单矢量直接功率控制SDPC（sin-gle-vector-based DPC）[4，6]，根据输入的有功和无功功率的误差及定子或转子磁链的位置，查找离线建立的控制表来得到较为合适的基本电压矢量。这种方法在依据转子磁链位置时，需要知道互感和转子电感，而依据定子磁链位置，可通过电压积分模型[7]并忽略定子电阻的影响来得到，此时并不需要电机参数。可以看出SDPC 相比于传统的矢量控制[8]和模型预测控制[9]拥有很强的参数鲁棒性。但是这种方法由于采用滞环比较器，只考虑了功率误差的方向而没有兼顾大小，在一个控制周期内仅作用单个电压矢量，故其稳态下功率脉动会很大，如果需要实现良好的稳态性能就必须采用很高的采样频率。此外，开关频率不固定也是其缺点之一。

为了改进单矢量的直接功率控制，有学者提出了预测直接功率控制P-DPC（predictive DPC）[10-11]，把一个控制周期分为3 块，在SDPC 选择有效矢量的基础上，另外选择一个有效矢量和零矢量，并重新计算各个矢量的占空比，来达到降低功率脉动和固定开关频率的效果。但是，在计算占空比的过程中，使用了大量的电机参数，其参数鲁棒性大大削弱。同时，另一些学者将空间矢量调制SVM（space vector modulation）技术引入直接功率控制[12]，由无差拍原则[13]直接得到所需的转子电压矢量，再用SVM 得到开关信号作用于转子侧逆变器上。这种方法相比于P-DPC，其省略了占空比重构，计算量小。但是同样地，这种方法的功率脉动小，开关频率固定，但对电机参数依耐性强。

为了在功率脉动、开关频率和参数鲁棒性之间找到一个折中，本文将占空比优化的思想[14]引入双馈电机直接功率控制中。在一个控制周期内作用一个有效基本矢量和一个零矢量，按照功率脉动最小原则计算各个矢量的占空比，可以称为双矢量直接功率控制DDPC（double-vector-based DPC），此方法功率脉动比传统单矢量直接功率控制小，计算量比P-DPC 小，参数依赖性比DPC-SVM 弱。

本文详细介绍DDPC 的基本原理和实现过程，并搭建实验平台对SDPC、DDPC 和DPC-SVM 进行算法验证，最后根据实验结果对3 种方法的性能进行比较，证明DDPC 能到达一个折中的控制效果。

1 双馈电机数学模型

双馈电机在转子坐标系中的数学模型可以用复矢量表示[15]为

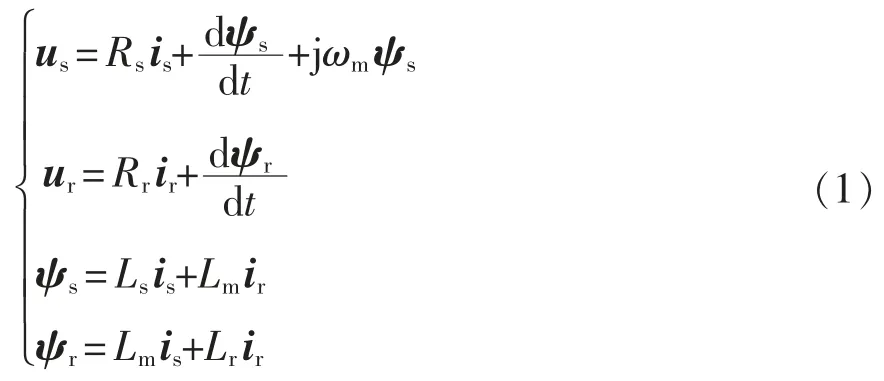
式中：us、is、ur、ir、ψs、ψr分别为定子电压、定子电流、转子电压、转子电流、定子磁链、转子磁链；Rs、Rr、Ls、Lr、Lm分别为定子电阻、转子电阻、定子电感、转子电感、定转子间互感；ωm为转子的电角速度。

2 直接功率控制

2.1 单矢量直接功率控制

传统SDPC 在一个控制周期内只作用一个矢量，可以是有效矢量，也可以是零矢量，其控制框图如图1 所示，并以图1 为依据对SDPC 进行介绍。本文采用两电平电压型变换器VSC（voltage source converter），其电压空间矢量如图2 所示。

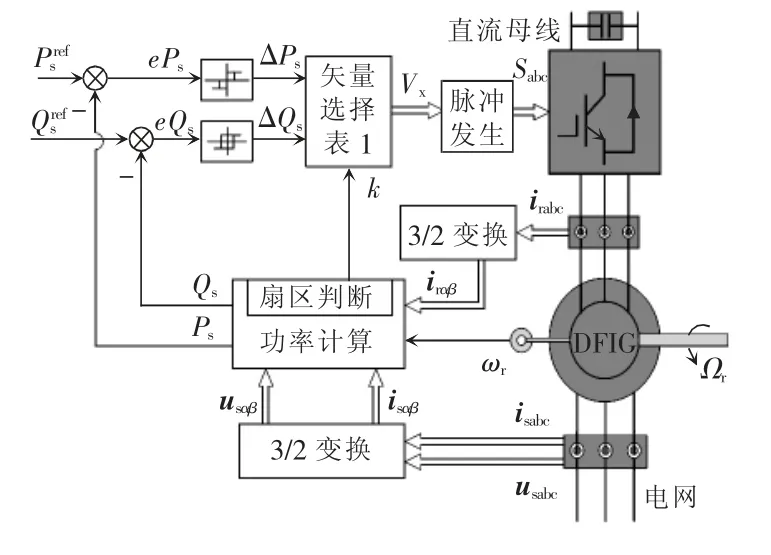
图1 SDPC 控制框图Fig.1 Control block diagram of SDPC

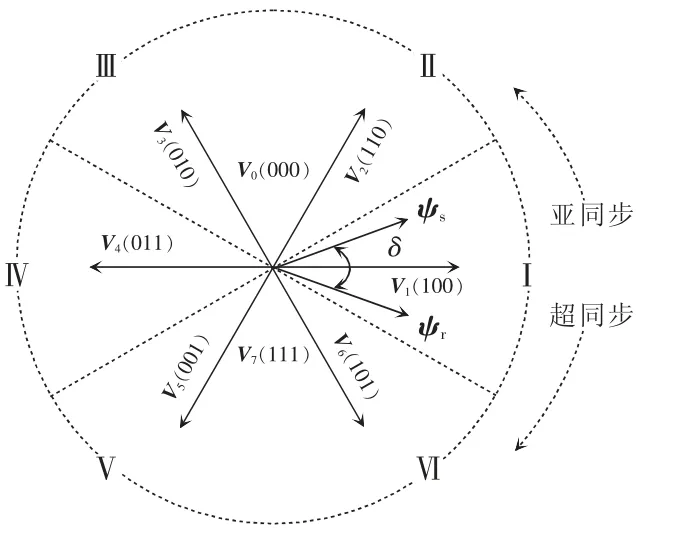
图2 两电平电压型变换器空间矢量Fig.2 Space vector of two-level VSC

双馈电机定子有功功率Ps和无功功率Qs的计算公式为

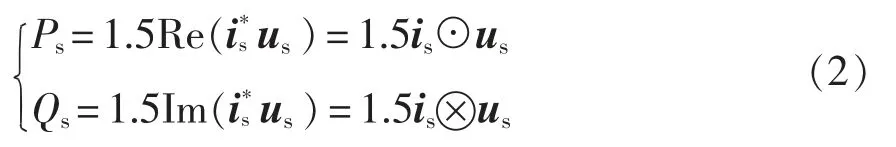
式中：⊙为点乘；⊗为叉乘；上标*为共轭。

将DFIG 的数学模型式（1）代入式（2）中，并忽略定子电阻，可以得到仅与定转子磁链有关的功率表达式，即

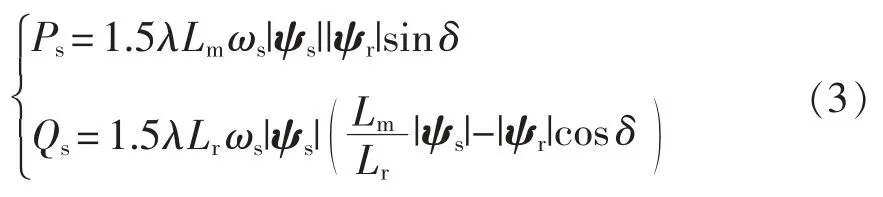
式中：ωs为定子侧电压角频率；δ 为定转子磁链之间的夹角；λ=1/（LsLr-为漏感系数。

由于双馈电机的定子侧直接与电网连接，所以可以假设定子电压恒定，进而可以将式（3）化简为

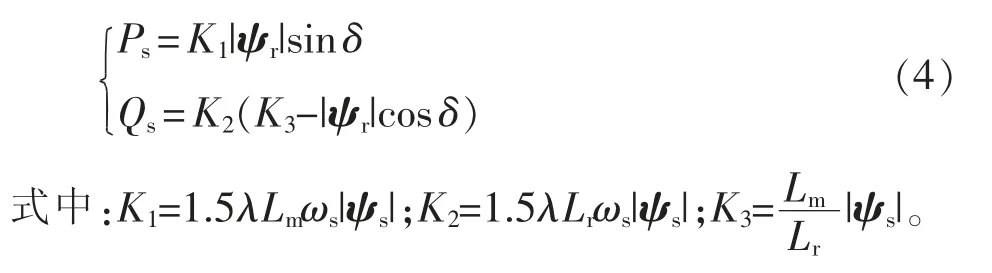
分析式（4）可以看出，定子有功和无功功率只跟转子磁链幅值和定转子磁链之间夹角有关，因此可以通过控制这2 个量直接对定子有功和无功功率进行控制，根据上文中定子电压恒定的假设，定子磁链的幅值|ψs|和角速度ωs都是恒定且已知的，此时定子磁链在转子参考坐标系中以恒定的速度旋转，可以认为其角度已知并以固定的规律变化，从而可以通过控制转子磁链的幅值与角度实现控制目标。进一步地，双馈电机由转子侧单独励磁，可以通过转子侧的变换器直接对转子施加不同的电压矢量，来调节转子磁链的幅值和角度。

转子电压矢量对定转子磁链的影响如图3 所示，两电平VSC 可以向转子施加8 个不同的电压矢量（V0、V1、V2、V3、V4、V5、V6、V7），通常在一个扇区内只有部分电压矢量是可以使用的。例如，图3（a）中转子磁链位于第I 扇区，此时共有6 个矢量（V0、V2、V3、V5、V6、V7）可供选择，图3（b）描绘了选择电压矢量V2时，转子磁链在很小的时间间隔h 内的变化情况。

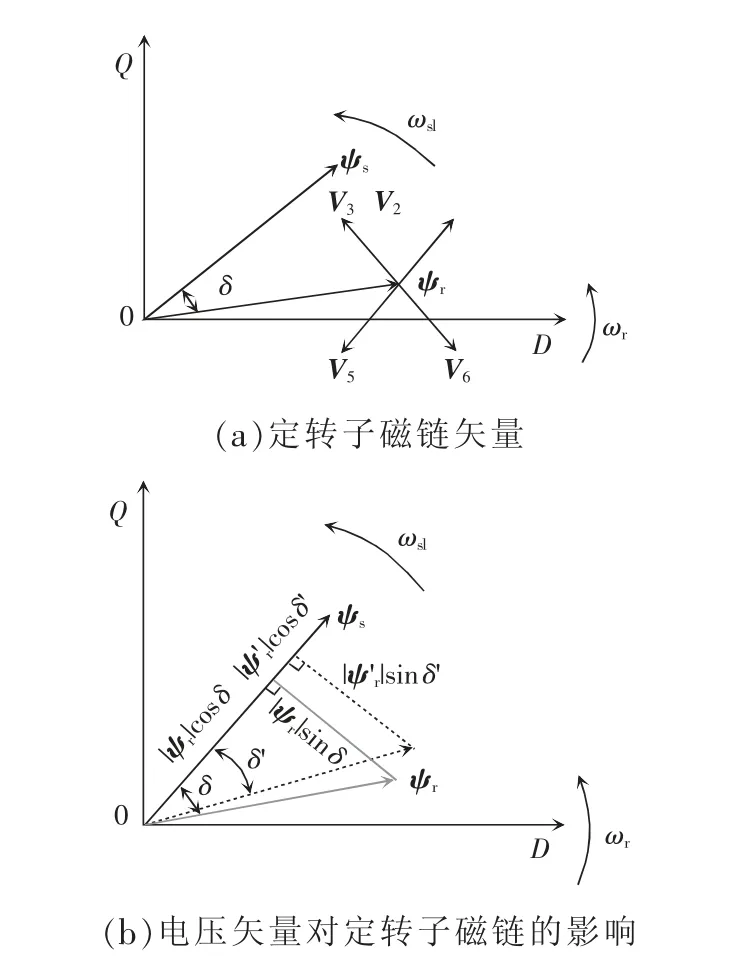
图3 转子电压矢量对定转子磁链的影响Fig.3 Influences of rotor voltage vector on stator and rotor fluxes

假设定子磁链在时间h 内没有变化，因此，施加电压矢量V2时，转子磁链幅值增大，定转子磁链夹角δ′ 减小，根据式（4），定子有功功率Ps和无功功率Qs均减小。此影响可表示为

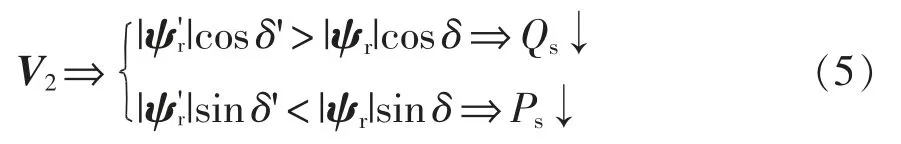
当在系统运行过程中连续施加不同的电压矢量时，转子磁链将跟踪定子磁链形成一个类似圆形的轨迹，当矢量作用的时间间隔h 更小时，得到的轨迹将更加接近于圆形，实现更好的稳态控制效果。

根据式（2），得到定子有功和无功功率的微分表达式分别为

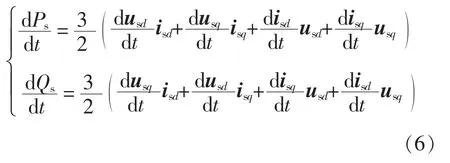
式中，下标d、q 表示转子坐标系d、q 轴分量。

将电机数学模型式（1）代入式（6）中，可以得到定子有功和无功功率的微分与定转子磁链夹角之间的关系为

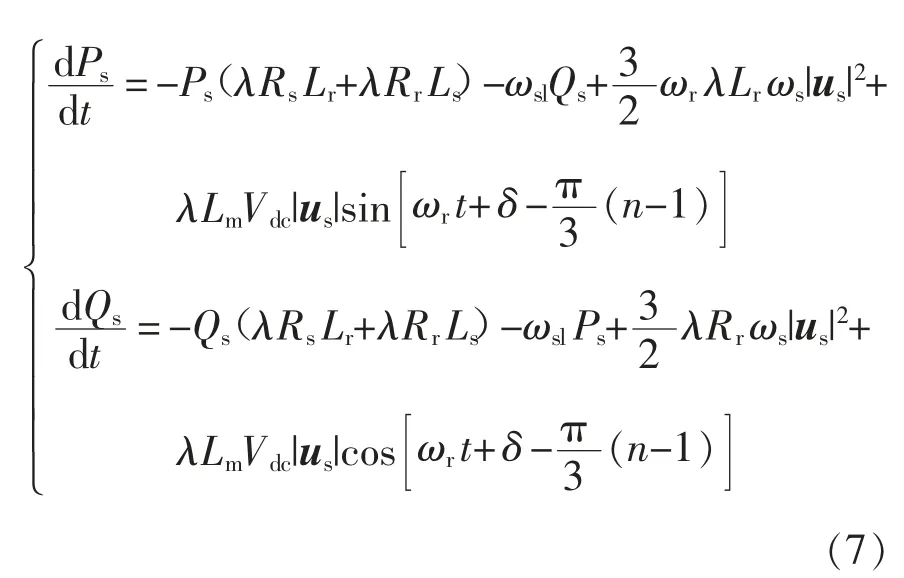
式中：Vdc为母线电压；ωsl为转子角频率，也叫转差频率，ωsl=ωs-ωm。定转子磁链夹角δ 可以计算为

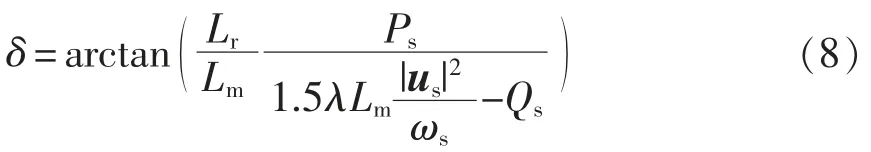
根据式（7）和式（8）可以得到各个转子电压矢量与电机定子有功和无功功率微分变化关系，如图4 所示，进而可以总结得到转子电压矢量的开关状态集，如表1 所示。

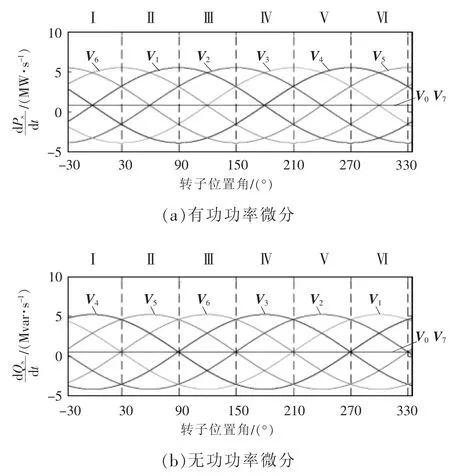
图4 亚同步速下有功和无功微分与转子位置角之间的关系Fig.4 Relationship between active/reactive power differential and rotor position angle at sub-synchronous speed

SDPC 采用滞环比较器得到定子有功和无功功率误差方向，也就是表1 中ΔPs和ΔQs，有功和无功功率控制器分别采用三阶和二阶滞环比较器，滞环宽度分别为HP和HQ，其结构如图5 所示。

表1 SDPC 转子电压矢量选择Tab.1 SDPC rotor voltage vector selection

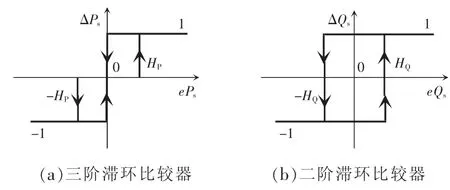
图5 直接功率控制采用的滞环比较器Fig.5 Hysteresis comparator for DPC

2.2 双矢量直接功率控制

传统SDPC 由于在一个周期内仅作用一个矢量，功率脉动在高采样率下仍然很大。为了解决这一问题，本节采用DDPC 方法。这种方法在一个控制周期内作用2 个电压矢量，包括一个有效矢量和一个零矢量，2 个矢量的作用时间根据一定的规则进行计算，大大降低了功率纹波，提高了系统的稳态性能。图6 为DDPC 的控制框图，本节将以此框图为依据对DDPC 进行介绍。

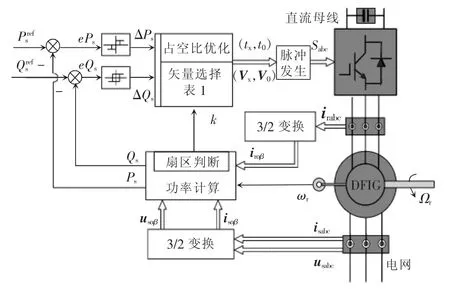
图6 DDPC 的控制框图Fig.6 Control block diagram of DDPC

通过对比图1 和图6 可以发现，2 种DPC 控制策略在很多方面都相同，采用同样的功率计算、扇区判断、滞环比较以及矢量选择环节，仅有的不同在于DDPC 比SDPC 多了一个占空比优化环节，因此在结构和计算等方面的复杂度并没有太多增加。另外要注意合理安排矢量的作用次序，减小开关频率以及开关损耗，提高系统整体效率。在调整矢量作用次序时，需要同时考虑2 个方面，一方面是在单个控制周期内选择合适的矢量组合来避免两相跳变，也就 是（V1，V0）、（V2，V7）、（V3，V0）、（V4，V7）、（V5，V0）、（V6，V7）；另一方面还要考虑2 个控制周期衔接时的矢量作用次序，例如上一个周期作用矢量组合为（V2，V7），当前周期所要作用的矢量组合为（V4，V7），那么需要将矢量组合的内部次序调整为（V7，V4），调整后2 个周期内的矢量次序从110—111—011—111 变为110—111—111—011，避免了一次单相开关跳变。

DDPC 最关键的还是在于最优占空比的获取，本节主要介绍基于功率脉动最小原则的DDPC。根据式（3），忽略定子电阻后用定转子磁链表示定子侧的复功率S 为

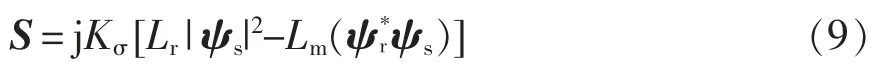
式中，Kσ=1.5λωs。根据电机数学模型式（1）以及式（9），可以得到复功率S 的斜率，即

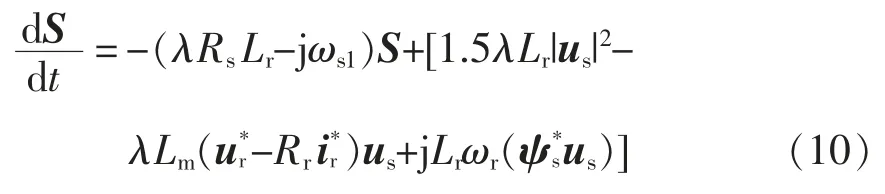
将式（10）的实部与虚部进行分解即可得到定子有功和无功功率的斜率。以稳态运行工况下有功功率的变化情况说明基于功率脉动最小原则的双矢量算法的基本原理，如图7 所示。将有功功率在有效矢量和零矢量单独作用时产生的斜率分别定义为s1和s2，无功功率在有效矢量和零矢量单独作用时产生的斜率分别定义为s11和s22，将一个控制周期内有效矢量的最优作用时间定义为topt，控制周期定义为Ts。

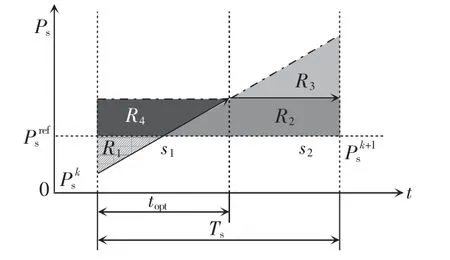
图7 稳态运行工况下有功功率的变化Fig.7 Variation of active power under steady-state operating condition

图7 中，当在一个控制周期内只作用一个有效矢量时，有功功率的脉动可以用区域R1、R2、R3进行表示，只作用零矢量时，有功功率的脉动可以用区域R1、R2、R4进行表示，作用2 个矢量（包括1 个有效矢量和1 个零矢量）时，有功功率的脉动可以用区域R1、R2进行表示，可以看出在一个控制周期内同时作用2 个矢量时，有功功率的脉动最小。与此同时，有效矢量作用的时间也会影响功率脉动的大小，接下来就以功率脉动最小为原则求取有效矢量最优作用时间topt。

对于双馈电机，需要同时考虑定子侧的有功和无功功率，因此，在采用DDPC 时，一个控制周期内的功率脉动Srip计算为

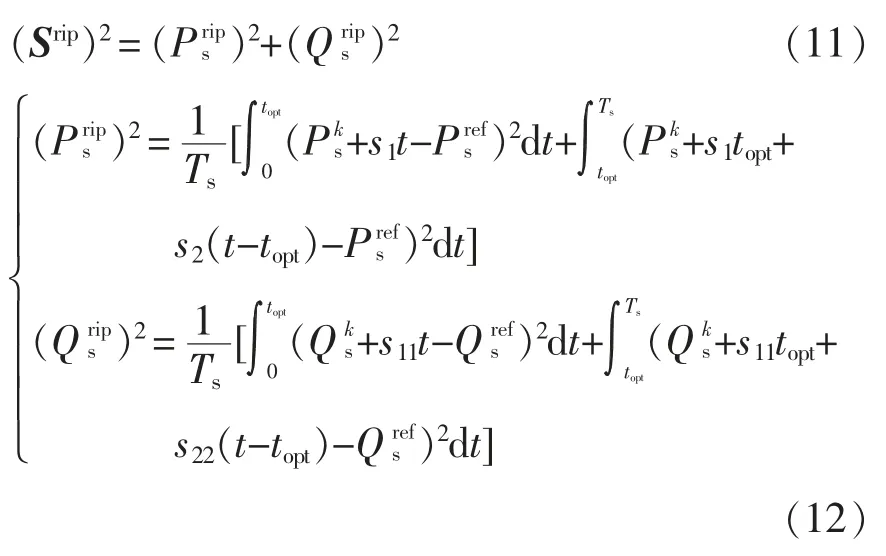
将式（12）对topt求导，可求得使Srip最小的作用时间topt为

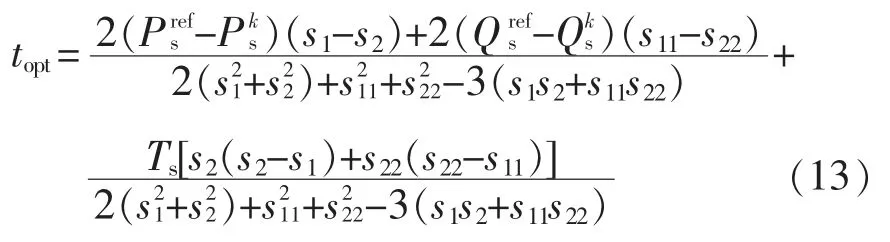
注意，topt＜0 时，topt应该设置为0；topt＞Ts时，topt应该设置为Ts。

3 实验结果和分析

本节对SDPC、DDPC 和DPC-SVM 这3 种方法进行实验验证和比较，其中SDPC 和DDPC 采样频率为20 kHz，DPC-SVM 采样频率为10 kHz，电机与系统的参数见表2。

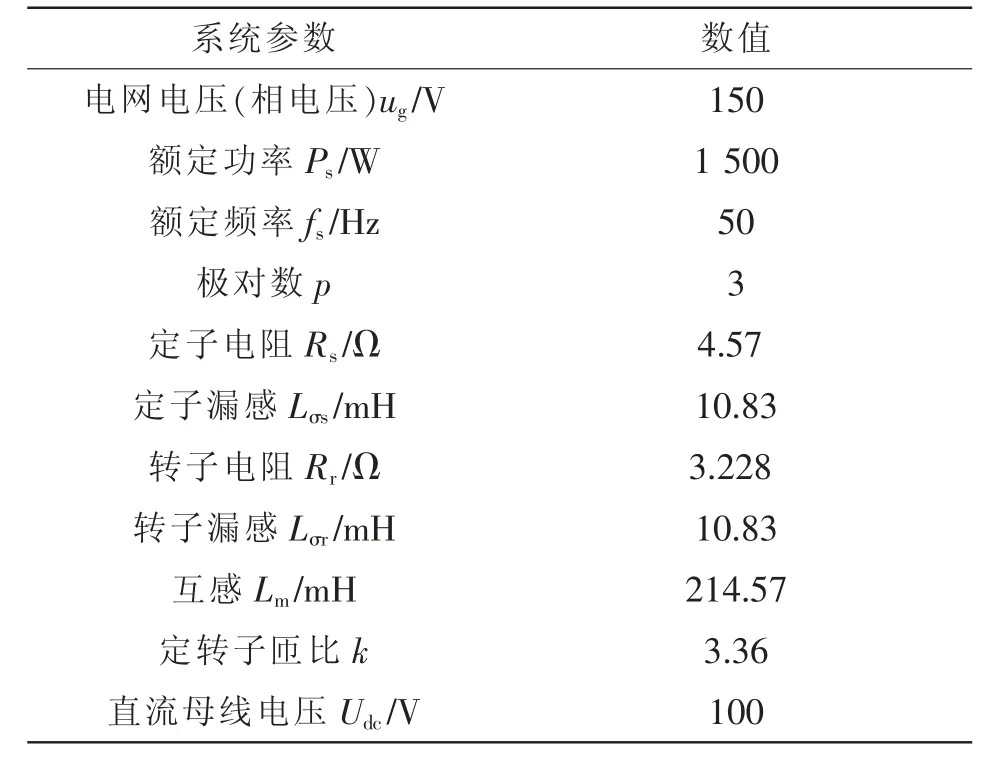
表2 电机与系统参数Tab.2 Parameters of motor and system

图8 为3 种DPC 方法有功功率阶跃的实验波形，图中变量自上至下分别为有功功率、无功功率、三相定子电流和三相转子电流。测试条件为电机转速700 r/min，在前100 ms 内有功和无功功率为0，电机处于并网状态但没有功率输出，100 ms 时有功功率从0 kW 阶跃到1 kW。对比图8（a）和8（b），可以发现DDPC 的稳态性能有了明显提升，功率和电流脉动更小，动态性能良好。再次对比图8（c）所示的DPC-SVM 方法，其有功和无功功率几乎没有明显波动，定转子电流的谐波也非常小，定子有功功率对于有功参考的跟踪同样十分快速，具有优异的动态性能。

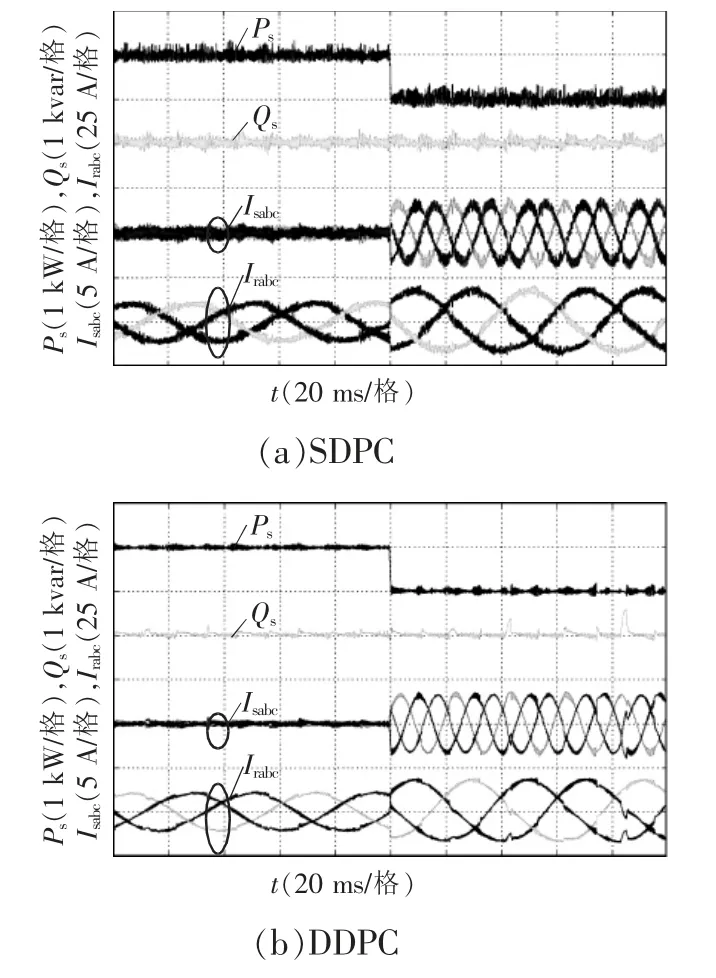
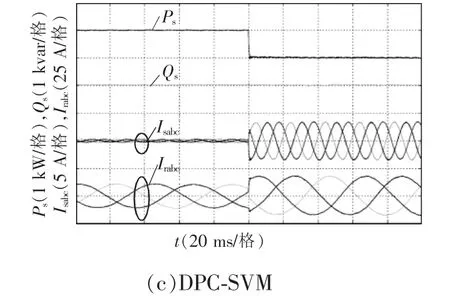
图8 有功功率阶跃实验波形Fig.8 Experimental waveforms under active power step

图9 为电机转速发生变化时的实验波形，此时电机的有功功率保持在500 W，转速从900 r/min 快速提升到1 100 r/min。可以清晰地看出，转子电流频率随转速变化而变化，在转速由次同步迅速提升到超同步的过程中，转子电流频率也由5 Hz 迅速减小到0 Hz，也就是直流状态，之后再快速恢复到5 Hz。转速变化前后，电机的转差角速度是不变的，因此转子电流只是发生了相序上的变化，其频率仍然能够恢复到之前的状态。与此同时，在整个动态变化过程中，定子电流保持恒定，其幅值、相位和频率都没有发生变化，没有发生脱网现象，有功功率输出保持平稳，没有因为转速的快速变化而发生波动。

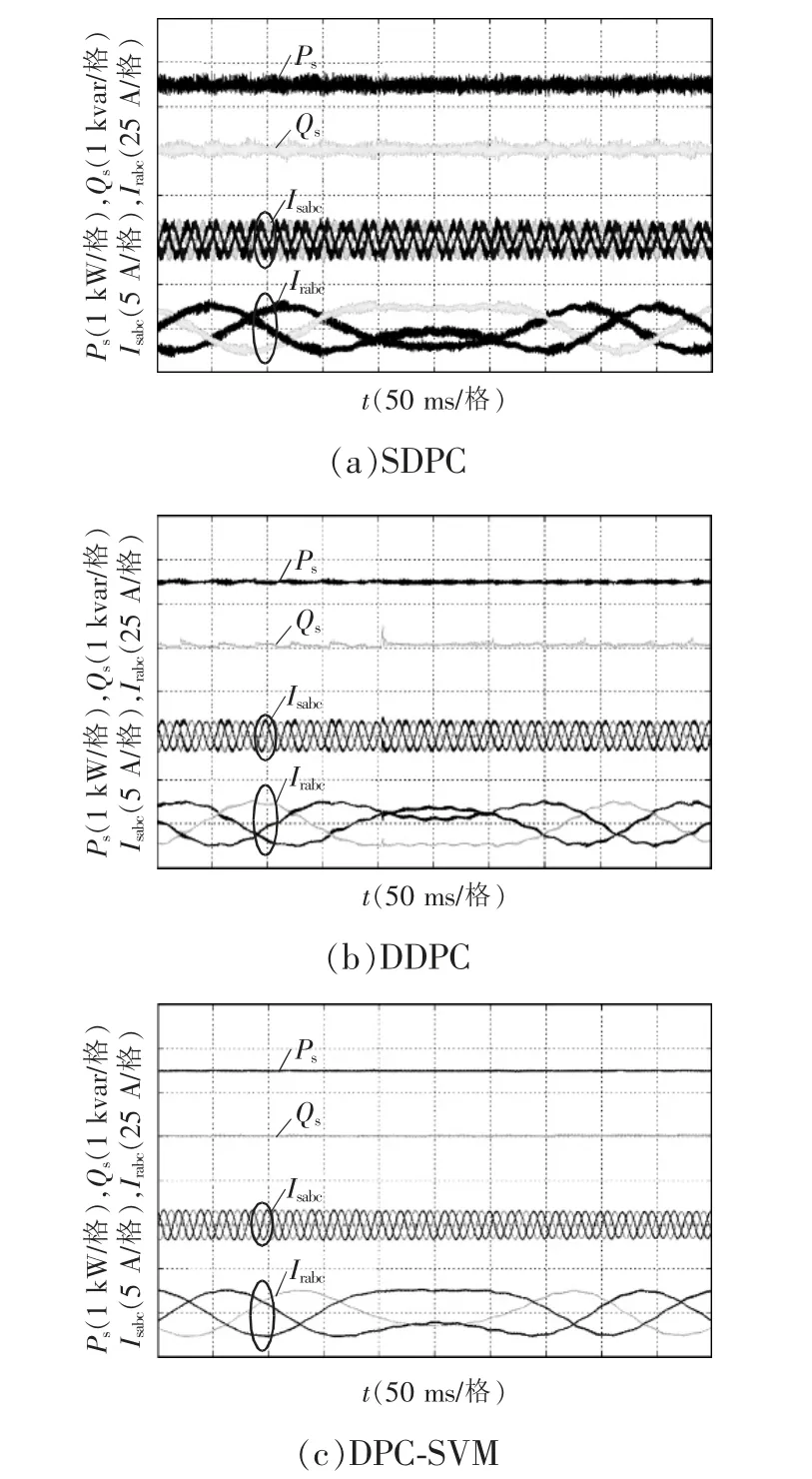
图9 转速变化实验波形Fig.9 Experimental waveforms with variation of rotational speed

图10 从3 种DPC 方法在有功、无功功率脉动、定子电流THD 和平均开关频率fsav这4 个方面的稳态性能分析。3 种方法中，在功率脉动和电流THD方面，SDPC 与其他2 种方法相比有很明显的差距，但是SDPC 的开关频率最低。DPC-SVM 虽然采样频率只有其他2 种方法的一半，但是由于SVM 的使用开关频率较高，稳态性能是三者中最好的一个。总的来说，3 种方法中SDPC 的稳态性能最差，开关频率最低。DPC-SVM 的稳态性能最优，同时其开关频率固定，而DDPC 的稳态性能相对SDPC 有较为明显的提升，但是其开关频率也有一定的升高。

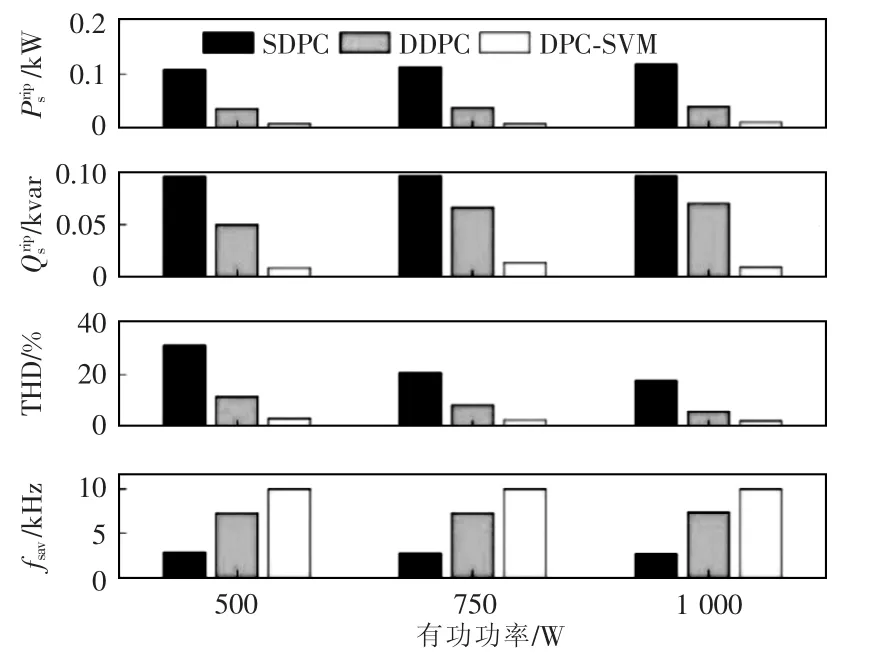
图10 稳态实验分析Fig.10 Steady-state experimental analysis

4 结语

本文为改善SDPC 稳态功率脉动大而DPC-SVM 对电机参数依赖性强的问题，提出基于占空比优化的DDPC。从实验结果可以看出，传统SDPC 结构简单，参数鲁棒性强，但功率脉动比较大，所需采样频率较高。DPC-SVM 可以在较低的采样率和固定的开关频率下实现很好稳态和动态性能，但开关频率有一定的升高，对参数依赖性大。而DDPC 的关键在于优化矢量占空比，采用功率脉动最小的基本原则进行占空比的计算，稳态性能相比SDPC 有较大提高，对参数的依赖性比DPC-SVM 小，属于3种控制方法的折中。实际中可以根据需求选择合适的控制方法。