基于磁控电感低压电网线电压调节器的研究

张继华，田 浩，陈忠华，王珂珂

（辽宁工程技术大学电气与控制工程学院，葫芦岛 125105）

线电压调节器LVR（line voltage regulator）是通过大量串联变压器来向线路接入额外的控制电压，这使得电路的电压出现大幅度波动，电压的传输效率和稳定性受到影响，因此针对该问题的研究具有现实意义[1-2]。基于可再生能源的分布式发电是我国能源利用可持续发展战略规划和环境保护的重要组成部分，大力发展分布式能源的同时，关于如何提高电压输送效率和稳定性是需要攻克的关键问题[3-7]。

关于电能传输线路中电压调节器的研究，国内外一些学者针对电压功率补偿以及对降低谐波失真等做了大量的研究工作，但对于电压的无极调节及实现高鲁棒性尚未达到理想的效果。文献[8-10]研究了动态电压调节器的方法及原理，通过补偿电压跌落相电压及补偿算法和控制方式来实现对电压的动态补偿；文献[11-15]研究了电压调节器对抑制电压波动、消除谐波畸变的建模与控制方法以及新型的改进方法；文献[16]研究了并联型动态电压调节器采用电压型变流器和双向直流变换器电路结构，利用超级电容作为直流侧的储能单元接入电网中，提高了电压的稳定性。

基于分布式能源供电，为改变控制电压，本文设计一种新型的低压电网线电压调节器，该器件采用磁控电感MCI（magnetically controlled inductor）元件，省去开关元件及其他运动部件的消耗，节约成本，也使得电压在调节范围内可以自由调动，系统的稳定性更高。并通过仿真及实验测试，得出模拟样机的性能、工作原理以及对电压的影响，可以实现电压的无极调节，且具有高鲁棒性的特点，使得该器件可以用于低压电网电路的调节。

1 模型结构设置

LVR 提供相反的相位电压以降低线路电压，图1 为馈线电压对线电压调节器的影响[17-18]。

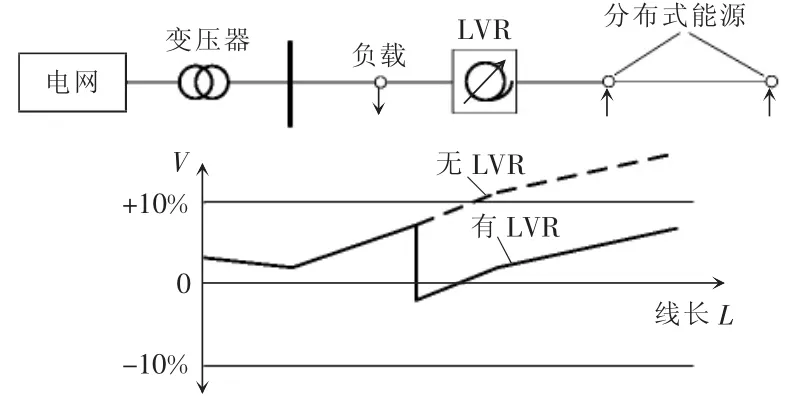
图1 LVR 工作原理Fig.1 Operating principle for LVR

基于目前的电网环境，低压电网电压调节器的主要目的是分布式能源电压馈入时在通过馈送端升高的时候降低电压有效值[19]。LVR 模型如图2 所示。图2（a）为该器件简化的单相模型。如图2 所示，电流经过器件模型从馈线侧到变电站，一次绕组和串联变压器的磁控电感构成该控制电路，该电路的电压表达式为

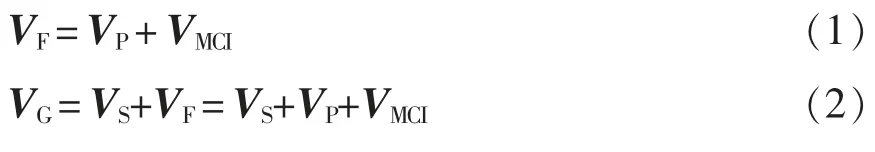
式中：VF为电流未进入电路之前的电流流入侧与接地线之间电压的差值；VP和VS分别为变压器高压侧和低压侧电压；VMCI为MCI 器件电压；VG为电流流入电路后与接地线之间的电压差值。

基于上述电压方程的向量如图2（b）所示，电压根据MCI 的不同电感得出。从向量图可以看出，MCI 的电感与电压呈反比关系，电感L 减小，导致电压VG上升。然而由于MCI 的电压角变化与饱和效应的关系，其电感的调整与馈线侧的电压VF不呈正比关系。

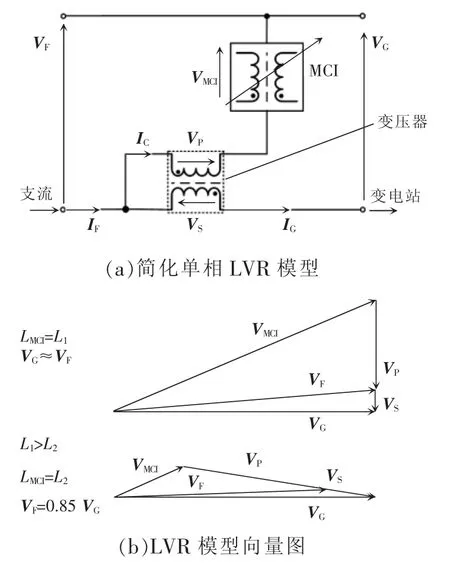
图2 LVR 模型Fig.2 LVR model

1.1 磁控器件模型

LVR 器件的MCI 模型是由一个环形变压器组成，匝数比N1/N2=1，铁芯内部有一个独立的控制绕组，并垂直于主线圈。通过控制绕组流过的直流电使变压器饱和。由于铁芯饱和程度增加，主线圈电感随之减小，所以主线圈的电感是通过改变控制电流的方式进行调节。图3 为MCI 的模型及磁通方向。

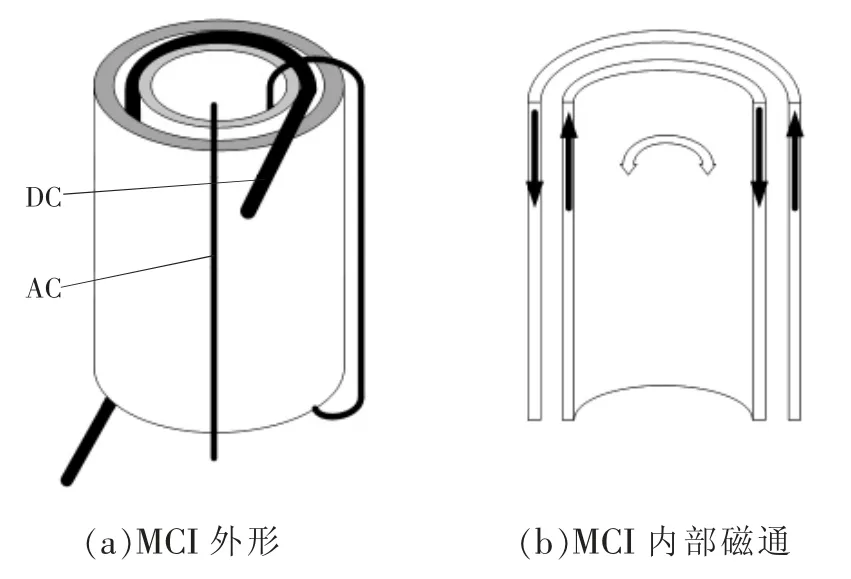
图3 MCI 模型建立Fig.3 Establishment of MCI model

1.2 电路模型

MCI 模型的三相电路与图2（a）不同，原因是MCI 连接在相互连接的星形绕组中。其优点是电压VMCI被平均分配在2 个MCI 上，这种情况下可以使用一个更小的铁芯，减少铁损耗和材料成本，体现了开发价值。图4 为简化电路原理，串联变压器的匝数比为9.8。

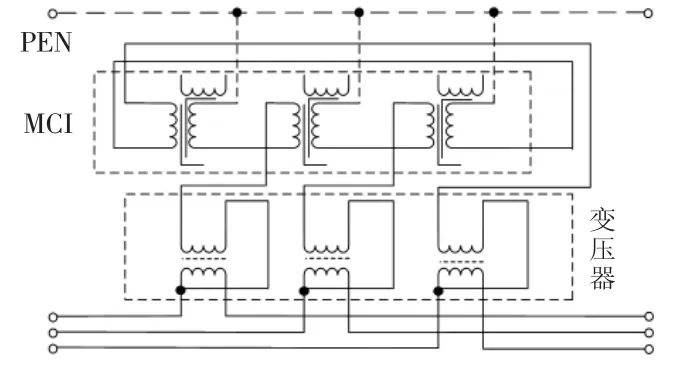
图4 简化电路原理Fig.4 Schematic of simplified circuit

1.3 实验平台

为了验证该理论的有效性和样机的工作原理、性能及其对电压的影响，在实验室基础上搭建了实验平台，如图5 所示。

图5 实验平台Fig.5 Experimental platform

2 LVR 硬件测试

基于电路原理，对LVR 进行建模。首先对串联变压器和MCI 进行一般的建模，这样就可以通过不同的连接变量以及不同的参数规格来设置几种工作模式。基于变压器的标准类型进行建模分析，变压器模型如图6 所示。如图6（a）所示，标准变压器模型包括初级线圈和次级线圈、绕组电阻R1和、漏感X1和以及铁芯电阻RC和主电感Xm。为了能够得到部分元件的阻抗，分别进行了变压器的短路和开路测试，其模型如图6（b）和（c）所示。

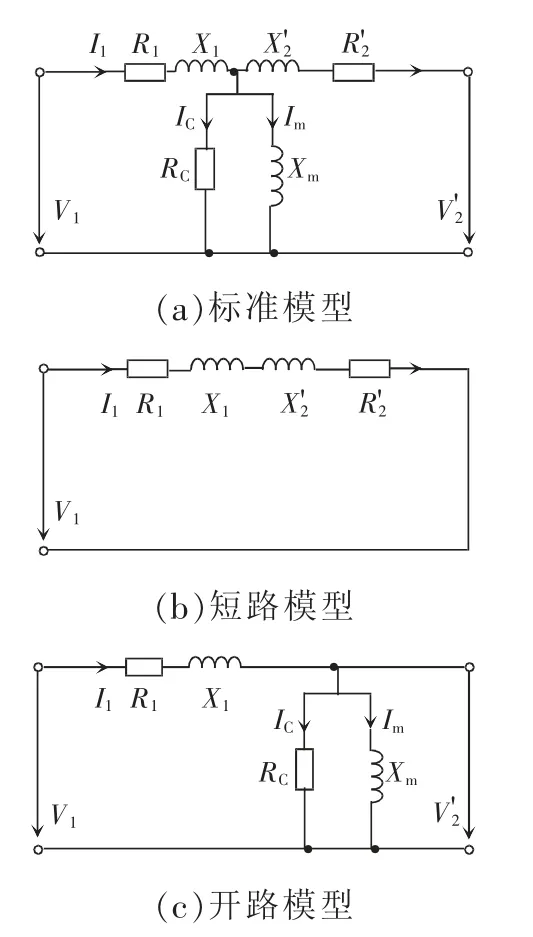
图6 变压器模型Fig.6 Transformer model

在一般情况下，线电压调节器以及变压器都工作在线性条件下，因此，标准模型能够代替实际样品。但如果MCI 被设置在饱和条件下工作，且依赖于控制电流的改变，则假定的标准模型是不够的。基于MCI 模型样机，通过实验数据分析表明，绕组电阻以及漏感都是线性的，与控制电流的变化没有关系，所以MCI 的分支电路不能用无源元件来设计。因而建立了一种具有磁滞磁芯元件的磁路与电路连接，如图7 所示。对于磁滞回路，基于Preisach模型使用Plecs 仿真，并由平滑函数表示。基于矫顽力HC、剩余磁力BR、饱和点的磁场强度Hsat、磁场密度，以及饱和磁导率μsat，生成一条磁滞曲线。图7（b）为具有相关定义点的滞回曲线。磁路元件的主线圈和二次线圈的匝数为N1和N2，截面积为A，电路长度为L。

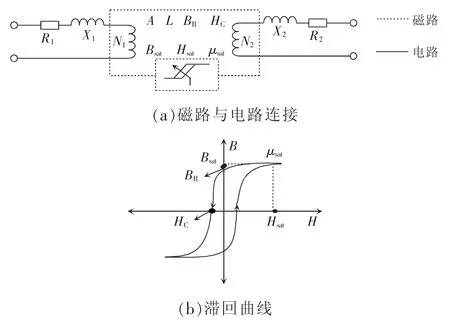
图7 电路模型Fig.7 Circuit model

将MCI 模型与串联变压器模型连接，在设置所有参数之后，连接到三相电路，组成样机模型，如图4 所示。通过开路试验和短路试验确定MCI 以及串联变压器的参数，并测量一次绕组和二次绕组的电压和电流。对于MCI 模型，由于只有磁性电感MCI DC 端的控制电流这一非线性因素，所以要用不同的控制电流来测试。

3 MCI 饱和效应研究

对于MCI 的分支电路，必须要进行开路测量。基于MCI 的电流和电压，确定H-B 滞回曲线的公式为

式中：H 为磁场强度；N 为匝数；l 为磁通路径的平均长度；I1为一次绕组电流；B 为磁通密度；A 为截面面积；V2为次级绕组上的电压。N、l、A 是固定的指定组件参数，在不同控制电流的情况下需开路测量I1和V2。

图8 为不同控制电流选择下的开路滞回曲线。由于控制电流的磁效应影响，能够产生额外的磁通，使得磁芯在主绕组中以较低的磁通密度饱和。随着提高磁路的控制电流，磁滞曲线被压缩，总电感减小。

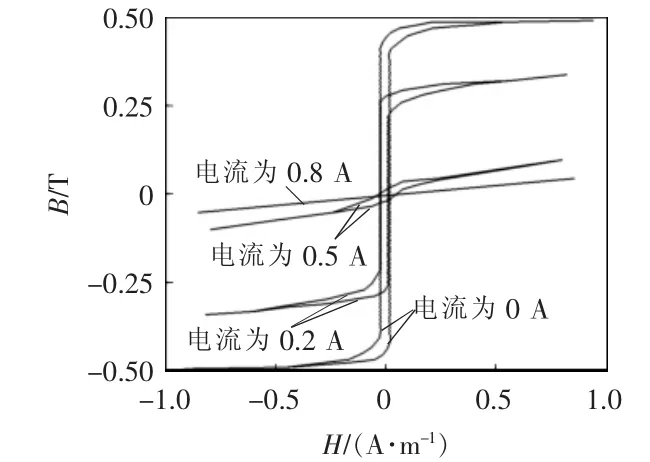
图8 开路滞回曲线Fig.8 Open-circuit hysteretic curve

图8 中，电流由下至上依次为0、0.2、0.5 和0.8 A。基于HC和BR对应的交叉点，确定了滞回曲线的定义点。又通过观察曲线的斜率，确定了饱和点的Hsat和Bsat。饱和区的斜率与μsat相对应，为了模拟不同情况下MCI 的工作性能，可以通过改变控制电流来改变磁场强度，产生不同的磁通密度，进而实现电压的无极调节，通过曲线拟合来计算控制电流与磁通密度之间的关系。

4 仿真验证测试

基于样机的静态特性，重点分析了该装置的功能特性。馈线侧相电压固定在0.4 kA 之间，电网侧连接2.8 Ω 的电力负载。模型输入的这种设置会产生从馈线端到电网的电流，该电流取决于样机的电压变化，控制在80～95 A 之间。仿真及性能测试结果如图9 所示。

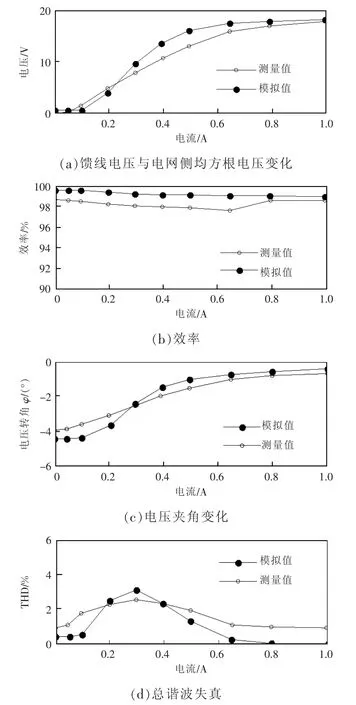
图9 仿真与测试结果Fig.9 Simulation and test result

图9（a）为馈线电压与电网侧均方根电压的变化，电压的最大差量为19 V，电压变化与控制不呈线性关系，所以在设计调节器时应考虑到出现的电流的影响。图9（b）为效率，由于MCI 电感降低，随着控制电路中电流的增长，效率随控制电流的增加而减小。最后2 个数据点是离群点，是由于测量期间馈线电压的5 V 压降引起的，最小效率约为98%。图9（c）为馈线电压与电网侧电压的夹角，当设备打开或关闭时，由于电压相位之间的关系，这些电压之间的电压角会导致系统能量传输效率下降，电压角的差值随控制电流的升高而减小。图9（d）为电网侧电压的总谐波失真，馈线侧电压有1%的谐波失真，所以样机主要增加了控制电流0.10～0.65 A 之间的失真。可以注意到，在存在较高的控制电流时MCI 的饱和效应会导致铁心完全饱和。总之，即使在最坏的情况下，样机模型仍然存在1.9%的失真。

图9 中，将模拟样机的性能与实测结果进行了比较，当控制电流大于0.3 A 时，模拟样机中的电压变化与测量值的差值约为2 V。仿真模型的效率比样机的效率提高了1%以上，电压偏角约为0.5°。一般情况下，总谐波失真在模拟和测量中会表现出相同的情况，建模样机主要增加了控制电流在0.10～0.65 A 之间的失真。此外，总谐波失真值比测量值小1%，是因为模拟中的电网电压是一个无失真的纯正弦波。为了能够更准确地表达该模型，对图2 所示的控制电路的电压和电流进行了仿真和实验室测试。图10 为控制电流0.3 A 的仿真结果。

由图10 可得，不同的模拟和测量MCI 电压VMCI之间的平均皮尔逊相关系数经过计算为0.953，这意味着存在着高度的线性相关性。由于Preisach 模型不能与MCI 的滞回曲线完全拟合，因而会出现偏差。由于寄生电路的影响，测量电压比模拟电压平滑得多。串联变压器的一次电压VP平均皮尔逊相关系数为0.973，而模拟VP的峰值平均比测量值高10%。仿真结果表明，模拟电压变化大于实测电压变化，这种偏差产生的原因是MCI 电压的误差和对寄生电路影响的疏忽。基于上述相同的原因，由于控制电路电流IC存在偏差，所以该电路的皮尔逊相关系数取0.935。仿真结果验证了该仿真模型具备足够的精度来表示原型的性能。

图10 仿真结果Fig.10 Simulation results

5 结语

基于现在分布式能源中控制电压的问题，本文介绍了一种新型基于磁性电感元件的MCI，并根据该元件设计了三相工作电路，分析了其在静态工作情况下的性能以及对电压的影响。通过改变控制电流来改变MCI 磁场强度，进而产生不同的磁通密度，实现电压的无极调节；通过相关皮尔逊系数的计算结果及仿真实验来验证其高度稳定性，使得该器件可以用于低压电网电路的调节。仿真验证证明了其性能即电压变化和效率达到了预期效果，具有电压无极调节的功能和高鲁棒性。然而其会对电压质量产生影响，即电压夹角和谐波失真，为避免出现故障，在以后的设计中应加以完善。