基于储能型开关电感准Z 源逆变器的模型预测控制

冯婷婷，张竣淇，朱 勇，周 平

（1.国网重庆市电力公司经济技术研究院,重庆 401120；2.重庆嘉汇投资有限公司新能源分公司,重庆 401120）

准Z 源逆变器QZSI（quasi-Z-source inverter）具有单级升降压、输入电流连续、电容电压应力减小等优点[1]。然而，QZSI 的升压能力仍明显不足，而引入开关电感后构成的开关电感型准Z 源逆变器SLQZSI（switched-inductor quasi-Z-source inverter）不仅能提高升压倍数、还提高了系统的功率密度，具有广阔的应用前景[2]。

一般情况下储能装置须通过额外的功率变换器连接至系统，以此增加系统灵活性和可调度性，但此类多级结构也导致系统冗余、可靠性降低。文献[3]尝试将电池直接连接到QZSI 的电容器C1或C2上，构成储能型准Z 源逆变器ES-QZSI（energy-storage QZSI），实现QZSI 与储能电池相结合，且不增加任何有源器件或功率变换单元，该方案克服了传统光伏系统中冗余的两级结构的缺点，在单级系统中实现了光伏发电与电池管理。

储能型系统具有可调度性和功率协调控制能力的优点，而SLQZSI 具有高升压比的优点，为了将两者优点相结合，本文提出将储能电池与SLQZSI相结合构成储能型SLQZSI，即ES-SLQZSI（energy-storage SLQZSI），该系统具备高升压能力的同时，也具备可调度性和功率协调控制能力。然而，储能电池的引入改变了SLQZSI 系统的两端能量平衡模式，即光伏输入功率和逆变器输出功率相平衡，ES-SLQZSI 系统中存在三端功率平衡：光伏电池功率、逆变器输出功率和储能单元SOC 平衡，系统控制设计变得复杂[4]，例如，电池内阻较小对并联电容的功率波动敏感[5]；电池放电模式下易导致电感L1电流断续[3]。这增加了控制器设计难度，且还未有适用的控制策略提出。

模型预测控制FCS-MPC（finite control set-model predictive control）在电力电子领域中的应用受到广泛关注[6-8]，其具备的优点有：动态性能优良；不设PWM 调制器，直接操作变换器开关；适用于被控变量较多的非线性系统；简单易于实现。已有研究将MPC 运用于未加储能环节的QZSI 系统中[9-13]。基于上述原因，本文针对ES-SLQZSI 提出基于FCS-MPC结构的功率控制策略。

本文首先建立ES-SLQZSI 离散化模型，基于此模型设计FCS-MPC 算法，设计光伏功率MPPT 模块和输出功率管理模块，在单级变换系统中实现升压、DC-AC 逆变、储能电池功率和光伏电池MPPT及并网功率三端能量控制。相比于传统DC-DC 加DC-AC 多级结构系统，该系统结构简单，无需额外的DC-DC 变换器；相比于传统双环PI+PWM 控制策略，该方法简单易行，不需要PWM 调制器，所需PI 控制器少；动态响应速度优良，适合被控变量较多的非线性系统。仿真结果验证了所提控制策略的有效性。

1 ES-SLQZSI 系统结构

图1 为带储能电池的三相开关电感型准Z 源光伏逆变器系统拓扑结构，由光伏电池、储能电池、开关电感型准Z 源阻抗网络[9]、逆变器以及交流电网组成，储能电池与电容C1并联，阻抗网络连接至电压源逆变器VSI（voltage source inverter）直流链两端构成ES-SLQZSI。ES-SLQZSI 有2 种工作状态：非直通状态和直通状态，其等效电路如图2 所示。通过添加特殊的直通状态（桥臂同时导通）将光伏电压vin升高至期望的vdc，经过逆变器后并入电网，实现单级系统升降压和逆变[14]，其电压关系为

图1 ES-SLQZSI 系统拓扑Fig.1 Topology of ES-SLQZSI system

图2 直流侧等效电路Fig.2 Equivalent circuits on DC-side

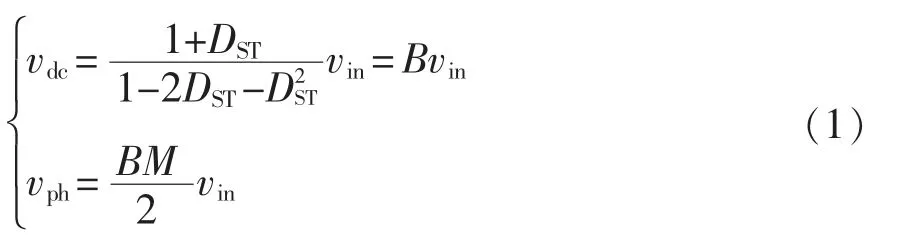
式中：DST为直通占空比；vph为相电压峰值；vin为光伏电池电压；B 为升压系数；M 为调制比。

为对比ES-SLQZSI 与传统QZSI 的升压能力，图3 绘出了升压系数B 与直通占空比DST的关系曲线，在DST＞0.3 的范围内，ES-SLQZSI 的升压能力明显强于传统QZSI。

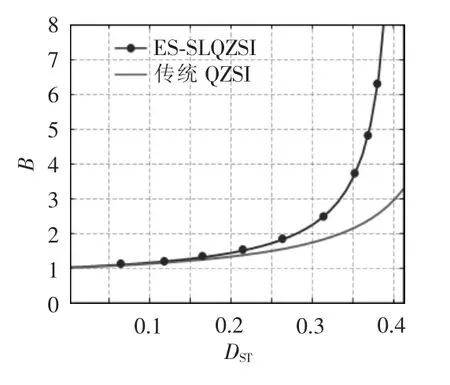
图3 与传统QZSI 升压系数对比Fig.3 Comparison of boost ratio with the conventional QZSI

传统电压源逆变器共有7 种不同输出电压矢量，对应7 种开关状态，仅存在于图2（a）工作模式中，在此基础上加上图2（b）的ES-SLQZSI 特有直通状态，可得出表1 简化后的8 种开关组合[12]。将这8种开关组合按一定条件交替配合，便可以实现单级系统升压和逆变，则输出电压矢量Vo_x表示为

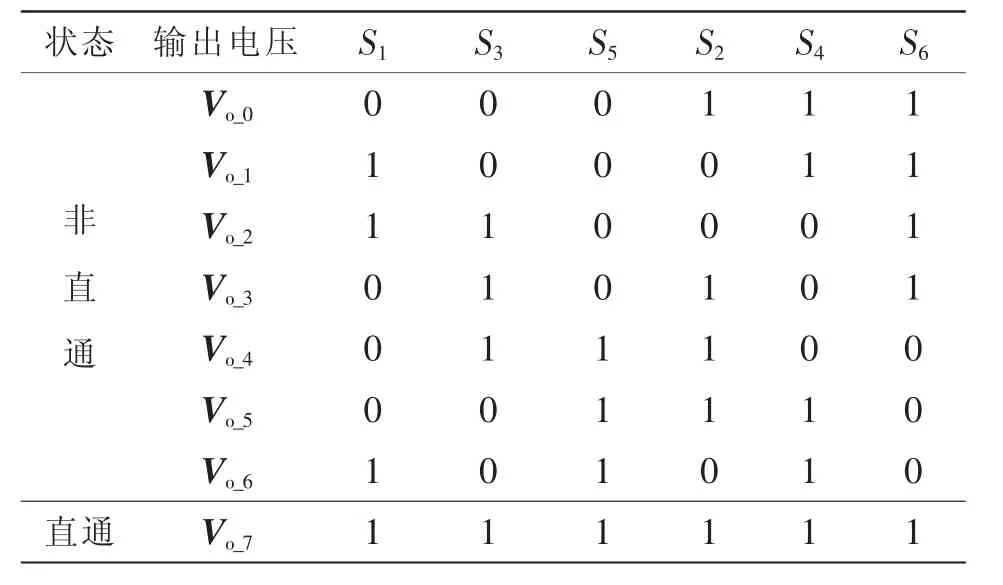
表1 ES-SLQZSI 在开关组合下的输出电压矢量Tab.1 Output voltage vectors of ES-SLQZSI under switch combination

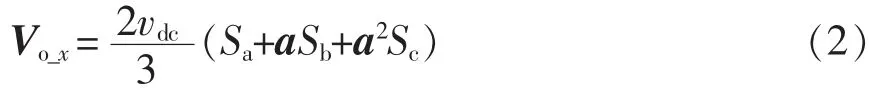
式中：a=ej2π/3；x=1，2，…，7；Sa、Sb、Sc为逆变桥三相开关状态，开通为1，关断为0。

根据基尔霍夫电压定律建立VSI 的回路方程，由图1 得αβ 坐标系下的方程为

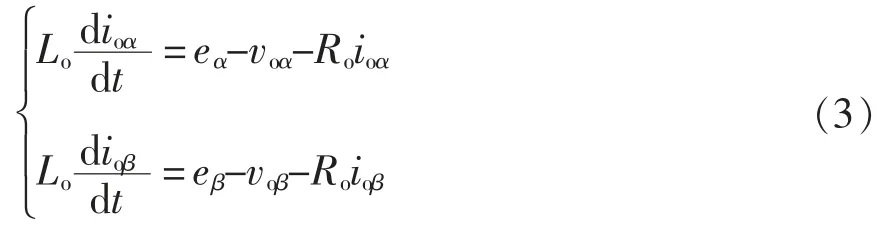
式中：ioα、ioβ为输出电流在αβ 坐标系下的分量；eα、eβ为电网电压在αβ 坐标系下的分量；voα、voβ为输出电压在αβ 坐标系下的分量；Lo和Ro为滤波电感和等效电阻。

2 ES-SLQZSI 的离散时间模型

模型预测控制是一种基于系统离散模型来预测控制变量未来行为的闭环优化控制策略[6]。根据预先设定具有最优化功能的代价函数，选取合适的门极驱动控制信号来控制逆变器。MPC 实现的第一步是建立ES-SLQZSI 系统离散时间模型，首先推导交流侧的离散时间模型，设信号采样周期为Ts，根据前向欧拉法，若Ts足够小，式（3）中输出电流的导数可近似为

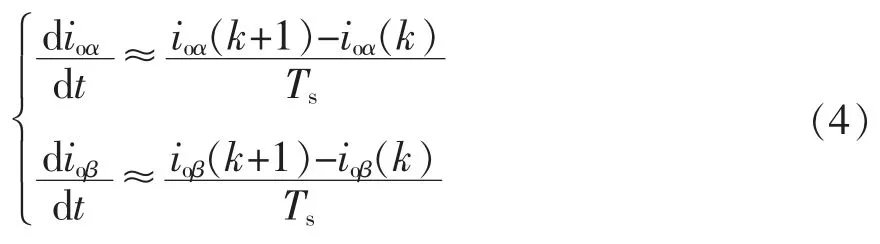
式中：ioα（k+1）、ioβ（k+1）为第k+1 个采样周期输出电流在αβ 坐标系下的分量；ioα（k）、ioβ（k）为第k 个采样周期输出电流在αβ 坐标系下的分量。

将式（4）代入式（3），得离散化表达式，即

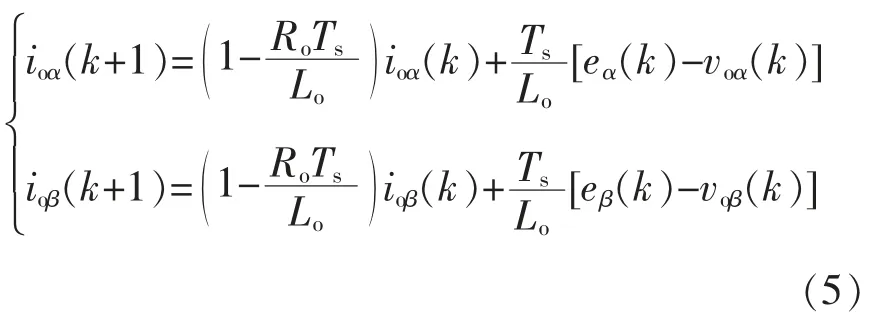
式中：eα（k）、eβ（k）为第k 个采样周期电网电压在αβ 坐标系下的分量；voα（k）、voβ（k）为第k 个采样周期输出电压在αβ 坐标系下的分量，对应表1。则有

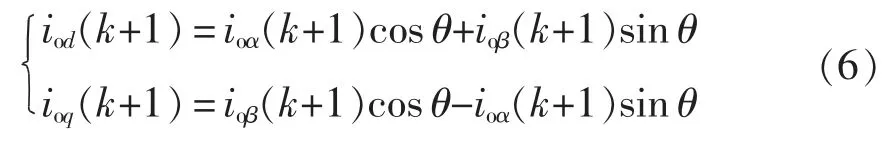
式中：iod（k+1）、ioq（k+1）为预测输出电流在dq 坐标系下的分量；θ 为电角度。

然后，推导ES-SLQZSI 直流侧离散时间模型，直流侧有直通和非直通2 种离散时间模型。

（1）非直通状态时，其等效电路如图2（a）所示。系统交流侧等效为一个开关和电流源并联[7]。二极管D1、D3导通，D2、D4关断，电感L2和L3串联，光伏电池vin和电感L1、L2、L3给交流侧和电容供电，等效开关S 断开。电感L1电压微分方程为

式中：iL1为电感L1电流；vC1为电容C1电压。根据式（4），可得式（7）电感电流iL1的离散形式为

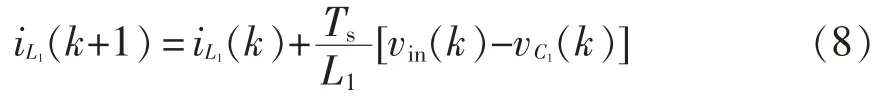
式中：vin（k）、vC1（k）、iL1（k）分别为第k 个采样周期光伏电池电压、电容C1电压、电感L1电流；iL1（k+1）为第k+1 个采样周期电感L1电流预测值。

（2）直通状态时，等效电路如图2（b）所示。逆变桥导通等效为开关S 闭合，二极管D1、D3承受负电压而截止，D2、D4导通，光伏电池vin和电容C1、C2放电，电感L1、L2、L3储能，电感L2和L3并联。电感L1电压微分方程为

式中，vC2为电容C2电压。对于采样时间Ts，由式（9）得预测电感电流为

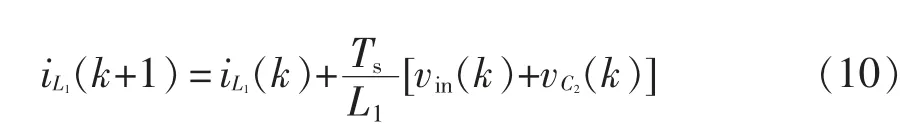
式中，vC2（k）为第k 个采样周期电容C2电压。

3 ES-SLQZSI 模型预测控制器设计

传统未加储能单元的SLQZSI 通常采用双环PI 控制策略，通过调节直通占空比DST实现升压和MPPT，通过控制调制比M 实现逆变，最终实现光伏输入和逆变器输出两端功率平衡[4-5]。储能单元的引入在增加系统功率分配灵活性的同时也增加了控制复杂度。引入储能单元后的ES-SLQZSI 系统变为三端功率平衡模式，表示为

式中，Pin、Pbat、Pout分别为光伏电池输出功率、储能电池功率、逆变器输出功率。Pin为正代表光伏电池向逆变器输出功率；Pout为正代表逆变器输出功率；电池释放功率时Pbat为负，当电池吸收功率时Pbat为正。只要控制3 个功率流中的2 个，第3 个功率就会匹配功率差额实现功率平衡。基于电网电压定向法，即eq=0，三相并网逆变器在dq 坐标系下的有功功率Pout和无功功率Qout为

式中，ed、eq为电网电压在dq 坐标系下的分量。由式（12）可知，并网有功功率和无功功率由iod、ioq控制，单位功率因数并网情况下ioqref恒等于0，分别表示为

式中：iodref、ioqref为输出电流dq 轴参考分量；Poutref为输出功率参考值。

本文提出的ES-SLQZSI 模型预测控制结构如图4 所示。整个控制结构由光伏MPPT 模块、输出功率控制模块、代价函数g 和预测函数f 组成。根据并网需求初始设定输出功率参考值Poutref，由输出功率计算式（13）获得dq 坐标系下输出电流幅值指令iodref、ioqref。光伏MPPT 模块采用扰动观测法追踪光伏电池最大功率点电压，并获得光伏电池电压参考值vinref，与实际电压vin的误差通过PI 补偿器与电感电流iL1ref解耦，光伏电池功率Pin=vinrefiL1ref，电感电流反映了光伏输入功率的大小，通过控制电感电流来控制光伏电池输入功率。剩余的功率差额Pbat则由储能电池进行释放或吸收。

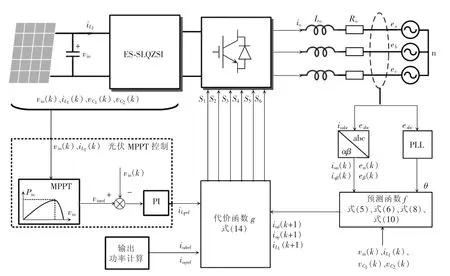
图4 ES-SLQZSI 控制框图Fig.4 Control block diagram of ES-SLQZSI

模型预测控制算法流程如图5 所示。控制环开始时测量第k 个采样周期的iL1（k）、vin（k）、vC1（k）、vC2（k）、ioabc（k）、eabc（k），三相电压和电流经坐标变换后得到αβ坐标系下的ioα（k）、ioβ（k）、eα（k）、eβ（k）。光 伏MPPT 控制模块和输出功率计算模块分别产生参考信号iL1ref和iodref、ioqref，然后用预测函数式（5）、式（6）、式（8）、式（10）去预测第k+1 周期8 种开关组合下的输出电流预测值iod（k+1）、ioq（k+1）和电感电流预测值iL1（k+1）。最后，将第k+1 周期的预测值与参考信号值代入代价函数g，当g 最小时所对应的开关组合即为最优的开关组合，第k+1 周期的被控量与参考值误差达最小。

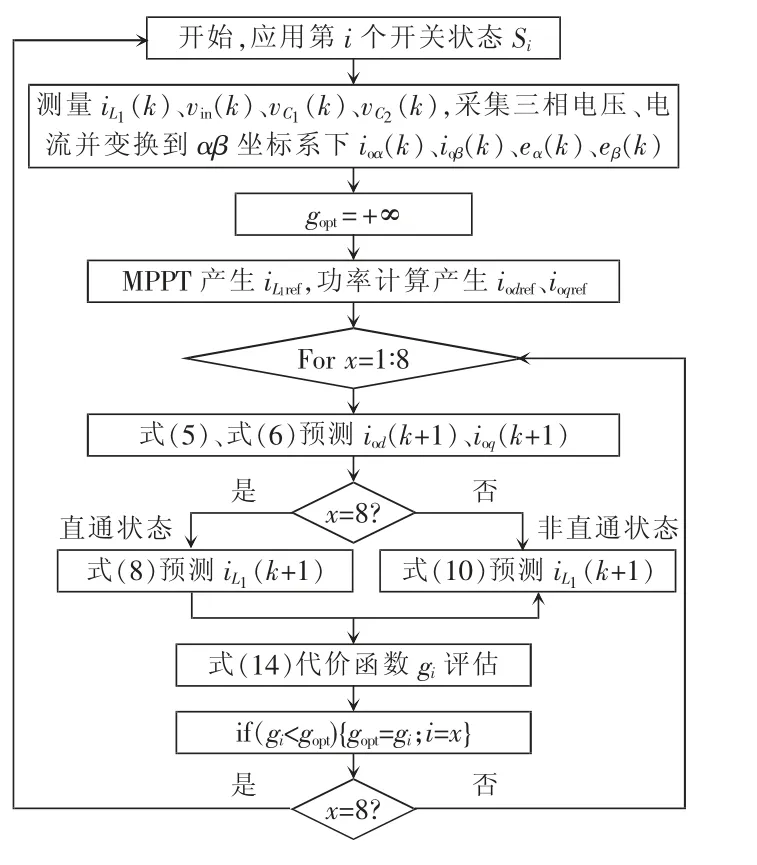
图5 控制算法流程Fig.5 Flow chart of control algorithm

满足本文功率控制要求的代价函数g 可表示为

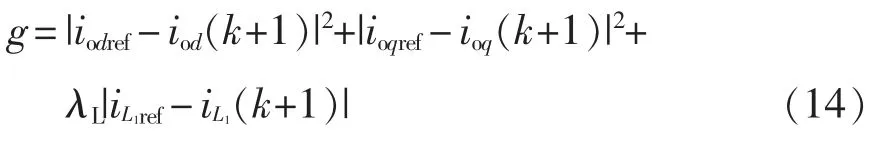
式中，λL为权重系数。调节λL可以调节系统动态性能。

4 仿真验证

利用Matlab/Simulink 搭建了图4 所示的详细仿真模型，对本文提出的FCS-MPC 的有效性进行仿真验证。系统关键参数如表2 所示。本文MPPT 采用变步长扰动观测法P&O（perturbation and observa-tion）。预测控制的开关频率是可变的，每个采样时刻开关状态仅可以改变一次，因此开关频率被限定在采样频率fs的一半，定义为平均开关频率，本文取为10 kHz[15]。模型MPC 算法程序根据图5 编写。

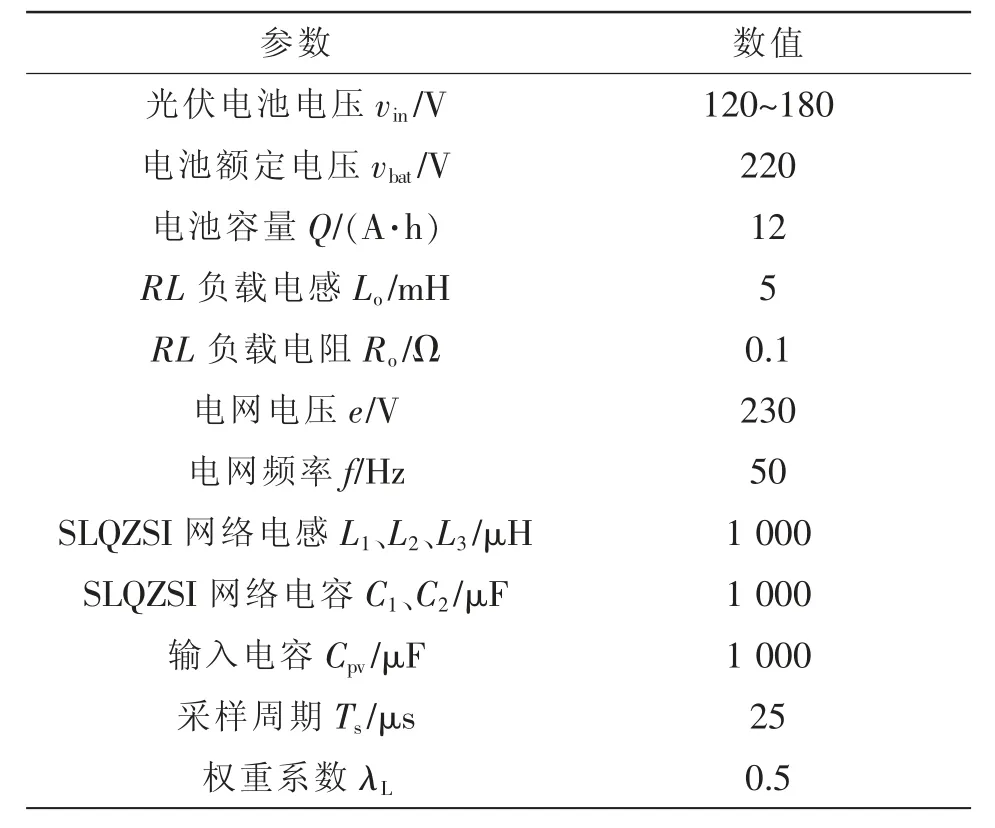
表2 系统关键参数Tab.2 Key parameters of system

4.1 升压能力对比

为对比2 种拓扑的升压能力，在同一输入电压vin=120 V 下改变直通占空比DST。DST分别为0.30、0.33、0.36 时对比结果如图6 所示，可见ES-SLQZSI的升压比B 分别为4.0、5.6、8.9，传统QZSI 的升压比仅为2.5、2.9、3.5，ES-SLQZSI 的升压能力优于传统QZSI。

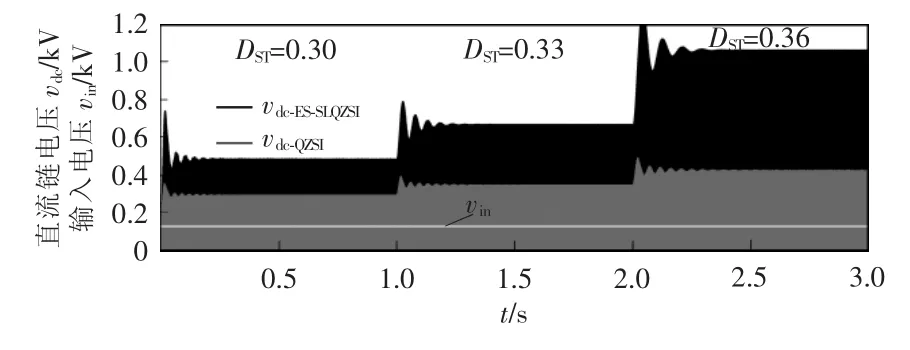
图6 2 种拓扑升压对比Fig.6 Comparison of boost capability between two topologies

4.2 稳态工作

仿真设定系统实现单位功率因数并网，给定并网功率参考值Poutref=2.0 kW、Qoutref=0 var（ioqref=0 A），光伏电池最大功率点电压为vinref=120 V，ES-SLQZSI 在FCS-MPC 控制下的稳态工作波形如图7 所示。图7（a）为功率流波形，系统此时从光伏电池收集能量并给电池与负载供电，光伏电池输出功率约2.6 kW，并入电网功率为2.0 kW，多余的0.6 kW 功率由电池吸收，满足功率守恒Pin+Pbat=Pout，验证本文所提系统能够实现光伏MPPT、电池储能、功率并网三端功率控制；图7（b）为光伏电池电压vin精确跟踪参考vinref=120 V 波形，图7（c）为电感电流iL1跟踪波形，验证本文所提控制策略能够对被控量实现精确跟踪；图7（d）为直流链电压vdc脉冲波形，由放大波形可见直通和非直通状态交替产生，从而实现升压与逆变，升压倍数为3.29 倍，实现了高升压比变换；图7（e）为a 相电网电压ea和a 相输出电流ioa，可见在FCS-MPC 控制下，ES-SLQZSI 的稳态运行效果良好，在单级系统中实现升压、逆变、单位功率因数并网和电池的精确控制。

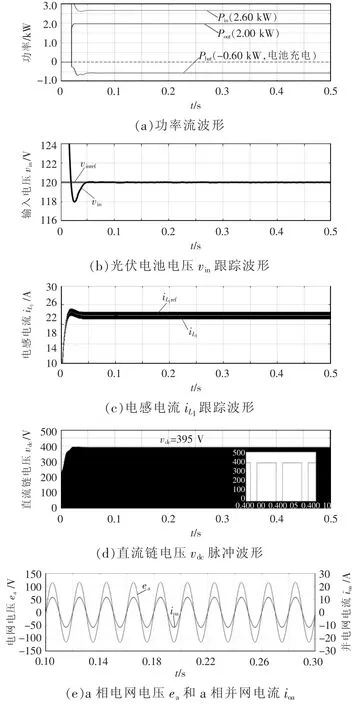
图7 ES-SLQZSI 稳态工作波形Fig.7 Working waveforms of ES-SLQZSI in steady-state

4.3 光伏功率波动

储能电池单元在光伏功率波动时能够起到削峰填谷的作用，为模拟此过程，系统在t=0.6 s 和t=1.2 s 时进行MPPT 控制，光伏电池输入功率Pin由1.60 kW 增大至2.65 kW，再降低至0.89 kW，而并网功率需求保持Pout=2 kW 恒定不变，储能电池弥补功率差额，如图8（a）所示；图8（b）、（c）为输入电压vin、电感电流iL1在MPPT 过程的动态波形，输入电压和电感电流均能精准跟踪参考，获取光伏电池输入的最大功率；图8（d）为a 相电网电压和电流波形，由图可见光伏功率波动时并网电流仍稳定无波动，与电网电压同频同相。仿真验证了光伏功率波动下系统仍能有效进行三端功率控制，保证提供平缓稳定的并网功率，即本文系统的优势所在。

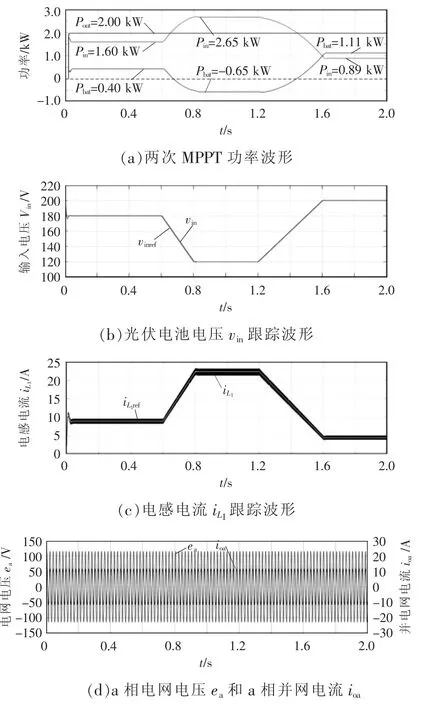
图8 光伏功率波动时的动态波形Fig.8 Dynamic waveforms under fluctuations in PV power

4.4 并网功率波动

为模拟并网功率变化时电池弥补功率缺额的动态过程，验证并网功率控制动态性能，在t=0.25 s时并网功率给定Poutref由2.5 kW 缓慢降至1.5 kW，光伏电池输入功率恒定为2.0 kW，即输入电压参考为vinref=160 V。如图9（a）所示，在输入功率不足以支撑并网所需功率时，电池放电0.4 kW 弥补功率差额，输入功率多于并网需求时则电池储存能量0.6 kW；图9（b）、（c）为输入电压和电感电流跟踪动态波形，由于电池功率弥补了并网功率差额，故其恒定不变；图9（d）为a 相电网电压和电流波形，输出功率在0.25 s 时减小，因此输出电流相应减小。仿真验证了并网功率需求变化时，系统能有效调节储能电池输出功率来弥补功率差额。

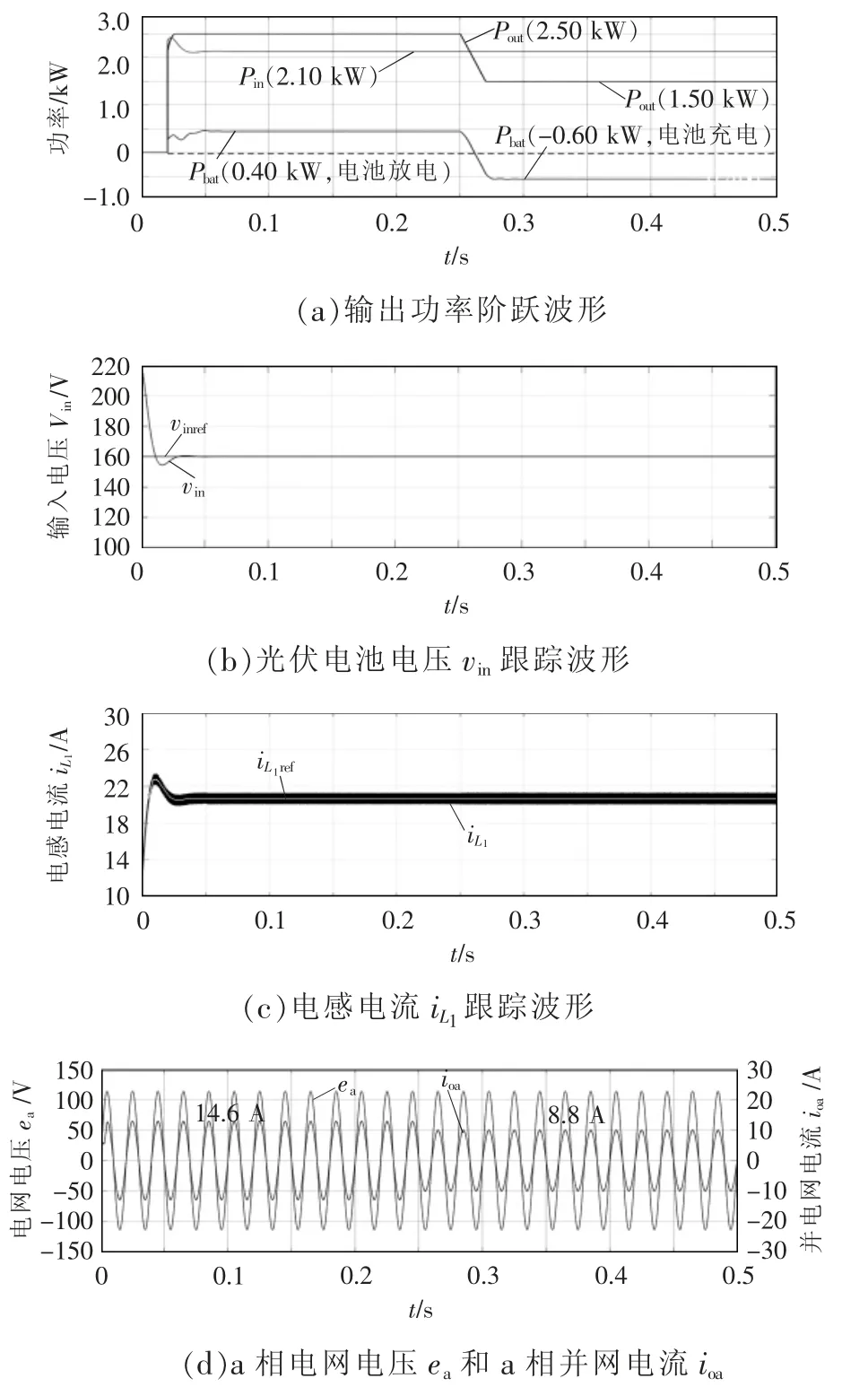
图9 并网功率变化时的动态波形Fig.9 Dynamic waveforms under changes in gridconnected power

4.5 动态性能

本文采用传统双环PI 控制实现了对ES-SLQZSI的功率控制，与本文所提控制策略进行对比。参考设置有功功率Poutref=2.5 kW、无功功率Qoutref=0 var；在t=0.25 s 时有功参考Poutref突降至1.5 kW，无功功率参考不变。传统双环PI 控制和FCS-MPC 控制下的有功、无功功率波形如图10（a）、（b）所示。由图可见，2 种控制方法均能实现并网功率的有效控制，FCS-MPC 控制下的功率瞬态过程响应速度快、无超调。图10（c）、（d）为2 种控制方法下的a 相电网电压和并网电流，FCS-MPC 控制下的电网电流响应速度快且无波动。验证了本文所提控制器具有控制稳定、响应速度快、鲁棒性高等优良的动态性能，提高了并网电流质量。

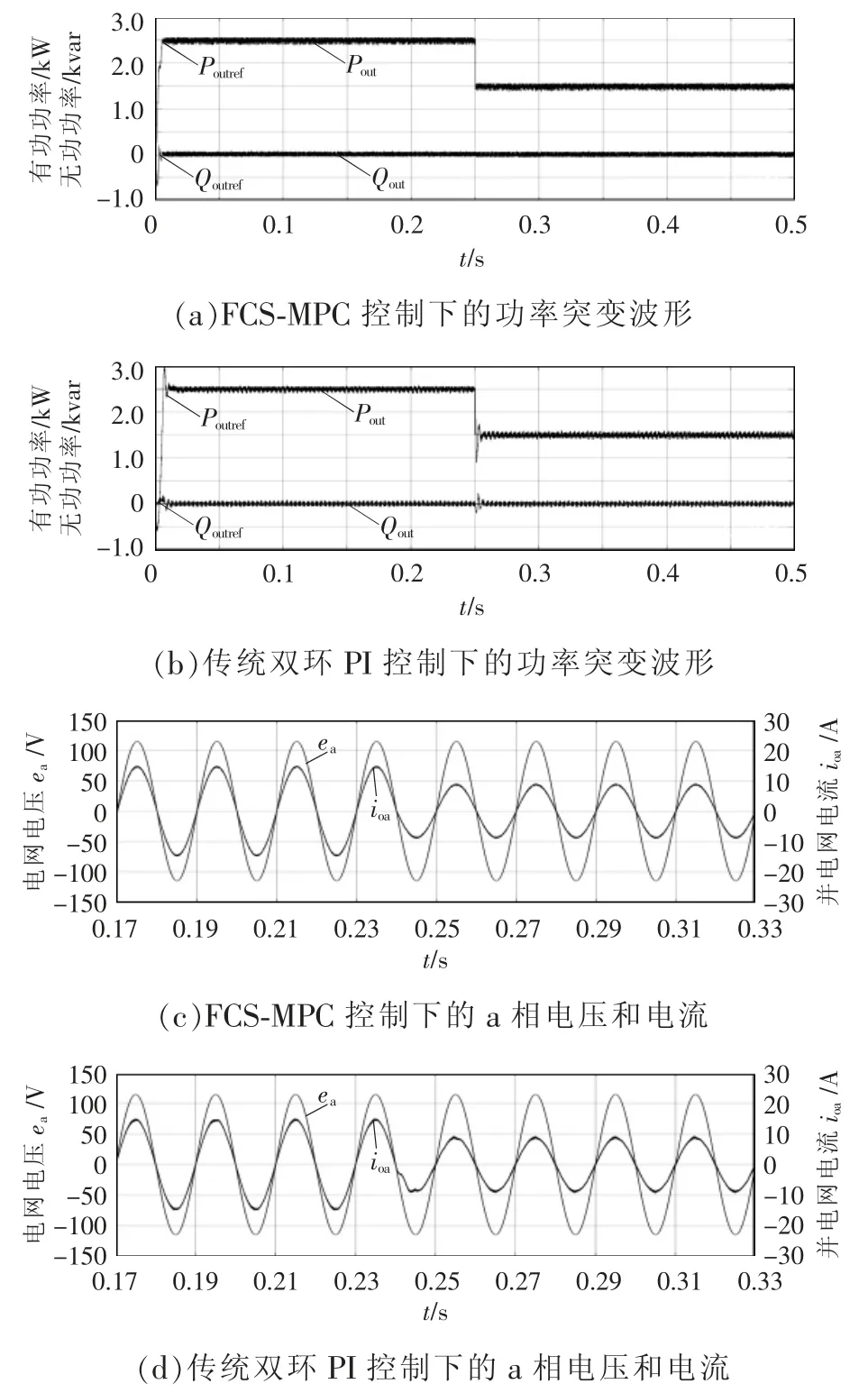
图10 并网功率突变时的动态波形Fig.10 Dynamic waveforms under abrupt changes in grid-connected power

5 结语

本文提出了基于FCS-MPC 结构的ES-SLQZSI功率控制策略。在QZSI 中引入开关电感提高了升压倍数，提出将SLQZSI 与储能电池结合构成ES-SLQZSI 系统，并采用FCS-MPC 控制策略在单级变换器中实现了光伏MPPT 控制、并网功率控制以及电池功率补偿。通过仿真对所提算法进行了验证。该系统结构简单，无需额外的DC-DC 变换器，能够实现单级升降压和逆变。相比于传统双环PI+PWM控制策略，该方法简单易行，不需要PWM 调制器，所需PI 控制器少；动态响应速度快、超调小，适合被控变量较多的非线性系统。