凿岩机瞬态冲击动力特性分析

丁问司,卿 涛

(华南理工大学 机械与汽车工程学院，广州 510641)

凿岩机是典型的以冲击破碎原理实现工作目的的特种机械，在公路及隧道施工中有大量应用。凿岩机活塞以一定速度冲击钎杆，使钎杆获得动能后冲击工作对象，并使其发生位移、变形、损坏，达到钻岩、破岩的目的[1-2]。针对凿岩机冲击动力特性的研究有助于提升凿岩机工作效率及提高凿岩装备的可靠性。

凿岩机冲击破碎系统可简化为由冲击活塞和钎杆组成的二元柔性杆冲击系统，其冲击过程中激发的应力波会在冲击活塞与钎杆中反向传播，并在约束面或边界面发生反射、透射现象，这使得各冲击部件将产生复杂形变，并伴随有瞬态能量传递。冲击过程结束后，冲击活塞和钎杆两端不受约束均成自由飞行杆进入分离状态。国内外学者对凿岩机工作过程的研究目前主要集中于流体驱动下活塞的加速、减速、反弹、缓冲等阶段的工作参数特性分析[3-5]，对冲击碰撞瞬间的动力学状态及其特性鲜有研究。然而，凿岩机工作过程中冲击活塞的断裂以及活塞前端面剥落等现象与冲击瞬态参数直接相关。改变结构参数可优化冲击部件冲击特性，改善工作过程中出现的相关问题。

近年来，对二元柔性杆共轴冲击问题的研究，部分学者采用特征线法对应力波的传播特性加以分析[6-8]，也有部分学者采用有限元数值计算进行冲击分析[9-11]。二元柔性杆撞击接触面冲击力的求解是冲击过程研究的关键内容。目前，有关计算冲击力的方法常为将冲击力视为外力，再通过冲击接触面位移连续性条件组建含未知冲击力项的微分方程[12]，以时间离散迭代法获得冲击力的近似计算结果。但该方法的计算过程复杂易引起收敛性问题[13]。

本文以柔性杆件振动瞬态波函数特征值展开法[14-15]来求解凿岩机冲击部件各截面在被冲击后的S-T函数，通过S-T函数变换求得各截面冲击力，避免了求解含未知力的强非线性方程。通过对不同参数条件下的变截面二元柔性杆冲击部件的受力状况及瞬态响应过程的分析，获得优化凿岩机结构参数和性能的方法。

1 凿岩机双杆件冲击动力学模型

凿岩机活塞与钎杆的冲击过程可等效为两柔性自由杆件共轴冲击的力学模型,如图1所示。冲击活塞以初速度v0冲击钎杆。钎杆和冲击活塞的弹性模量为E1、E2;密度为ρ1、ρ2;长度为l1、l2;截面积为A1、A2;质量为m1、m2。研究中设定各杆件为各向同性的线性弹性体，并忽略接触面的撞击变形。

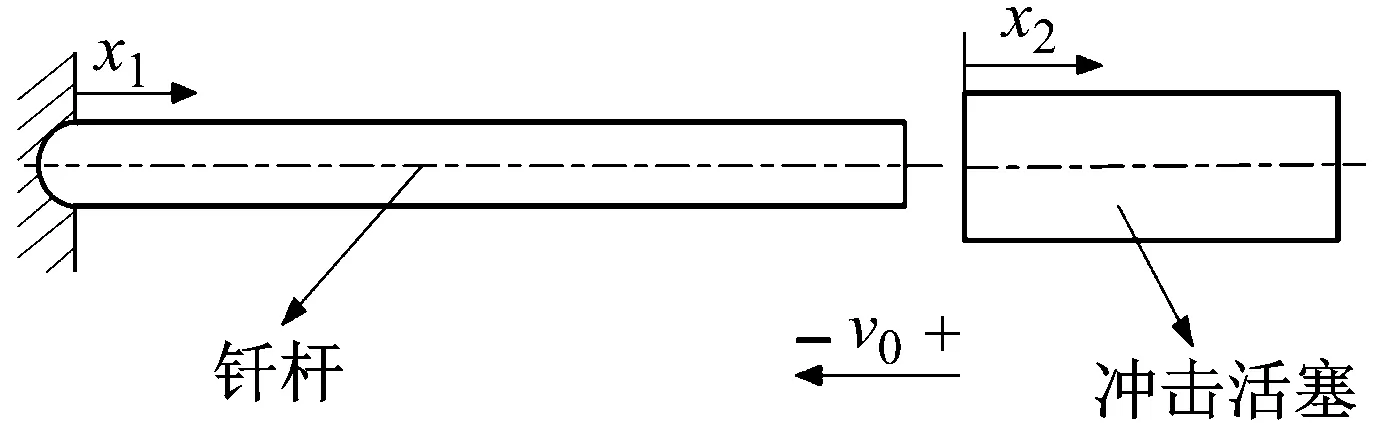
图1 冲击凿岩系统动力学模型Fig.1 Dynamic model of percussion drilling system

1.1 冲击过程S-T函数

设冲击发生后各部件的各截面每个时刻的位移为s(x,t)，由达朗贝尔原理可得冲击波动方程

(1)

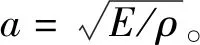
s(x,t)=S(x)·T(t)

(2)

式中：T(t)为运动规律时间函数；S(x)为冲击部件上x截面的纵向位移。

联立式(1)、式(2)求解得

(3)

令c=ω2有

(4)

(5)

1.1.1 冲击部件各纵向截面S函数

将式(4)拉氏变换后可求得钎杆和冲击活塞所满足的动态唯一解

S(x)=p·cos(kx)+q·sin(kx)

(6)

式中：k=ω/a;p和q为系数。

冲击时钎杆和活塞的边界条件和连续性条件为

σ1(x1,0)=0,σ2(l2,0)=0

(7)

s1(l1,t)=s2(0,t),A1E1σ1(l1,t)=A2E2σ2(0,t)

(8)

由式(6)～式(8)可得冲击过程中钎杆和活塞的特征方程为

S1(x1)=p1cos(k1x1)

(9)

冲击过程中，钎杆和冲击活塞结合为一体，两者有相同的固有频率，并可由式(11)求解。振动过程中冲击部件存在多阶振型，本研究实算中综合考虑计算量和计算精度选取前300阶振型进行分析，运算结果已具备较高精度[16]。

冲击过程中主振型关于质量的正交性条件为

(12)

式中,n为第n阶振型。

根据主振型关于质量的正交性求得

(13)

1.1.2 冲击部件冲击过程响应T函数

冲击过程初始条件为

s1(x1,0)=S1(x)·T(0)

(14)

s2(x2,0)=S2(x)·T(0)

(15)

v1(x1,0)=0,v2(x2,0)=-V0

(16)

将准静态S-T函数以及动态T函数代入式(5)得

(17)

通过拉氏变换，并利用主振型关于质量的正交性，可得T函数满足的表达式为

(18)

T函数初值可由初始条件及质量正交性条件求得

(20)

(21)

由此可得冲击过程柔性阶梯杆模型S-T函数为

(22)

式中：i为钎杆和活塞,i=1，2；n为各阶主振型,n=1，2，…，300。

冲击中活塞和钎杆的任意径向截面的速度为

(23)

截面轴力为

(24)

活塞、钎杆的轴力分布为

(25)

通过判断接触面所受冲击力的正负值可判断冲击结束时刻。当冲击力计算值由压力变为拉力，说明两杆分离，冲击过程结束。

1.2 分离过程S-T函数

活塞和钎杆冲击分离后，将以各自的固有频率进行振动。设分离后活塞和钎杆的运动方程为

(26)

分离后的活塞和钎杆均为自由飞行杆，其满足的边界条件为

(27)

(28)

分离后活塞和钎杆的主振型分别为

(29)

(30)

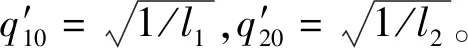
(31)

(32)

求解钎杆和活塞分离过程的时间函数与求解冲击过程中使用的方法相同，可将分离过程T函数代入式(17)，通过拉氏变换以及分离过程中的质量正交性求得。

分离过程中的S-T函数及速度、应力时间函数可通过式(22)、式(23)、式(25)求得。

1.3 凿岩机凿入力及冲击能量利用率

1.3.1 凿岩机凿入力

凿岩机钎杆截面轴力是钎杆受活塞撞击产生的入射应力和反射应力以应力波形式反复在杆内传播和叠加后，在各任意横截面形成的轴向力。在活塞撞击后的不同时间段，钎杆截面轴力将沿钎杆横截面产生不同的分布。钎杆中钎头端截面处的应力波传播叠加后形成的轴向力将作用于凿岩工作介质，由此形成凿岩机凿入力[17]。凿入力是凿岩机性能的衡量标准之一。

1.3.2 冲击活塞能量利用率

冲击活塞以速度v0和钎杆碰撞后，将在钎杆中建立应力波σ1自右向左传播，在活塞中也将建立应力波σ2自左向右传播，当t=2l2/α时,活塞中应力波自活塞自由端反射至活塞-钎杆界面，并向钎杆入射一个大于钎杆应力波的拉应力。

钎杆中n阶入射应力波的方程为

(33)

式中，γ为反射系数。

钎杆中入射应力将致钎杆中总应力变为正值。因活塞不能拉伸钎杆，当钎杆应力降为零时活塞钎杆分离，活塞入射应力波停止射入，此时活塞冲击能量不能全部透射于钎杆中，即钎杆不能将活塞能量充分利用。

钎杆中入射波能量Ti

n=1,2,3…

(34)

活塞中的冲击能量T0

(35)

Ti仅为活塞冲击能T0的一部分，存在活塞能量射入不完全的情况。

活塞能量利用率η

η=(Ti/T0)·100%

(36)

2 凿岩机瞬态冲击动力响应分析

2.1 试验结果与理论仿真结果对比

研究中在冲击试验台上以高速压气枪模拟凿岩机活塞的单次撞击特性，每次试验前将冲击活塞置于压气枪管中，通过气枪管中的气体对冲击活塞做功，使得活塞以不同冲击速度撞击被测钎杆。工作时开启快速切换阀，进入枪管的高压气推动冲击活塞使其加速至出口冲击钎杆。压气枪管出口端设置有激光探头和测速仪，活塞冲击时其冲击端面先后经过两组激光探头并触发“遮光”信号，测速仪根据“遮光”信号时间差及激光探头组的水平设置距离可得出冲击活塞的冲击速度。试验中冲击装置系统原理，如图2所示。

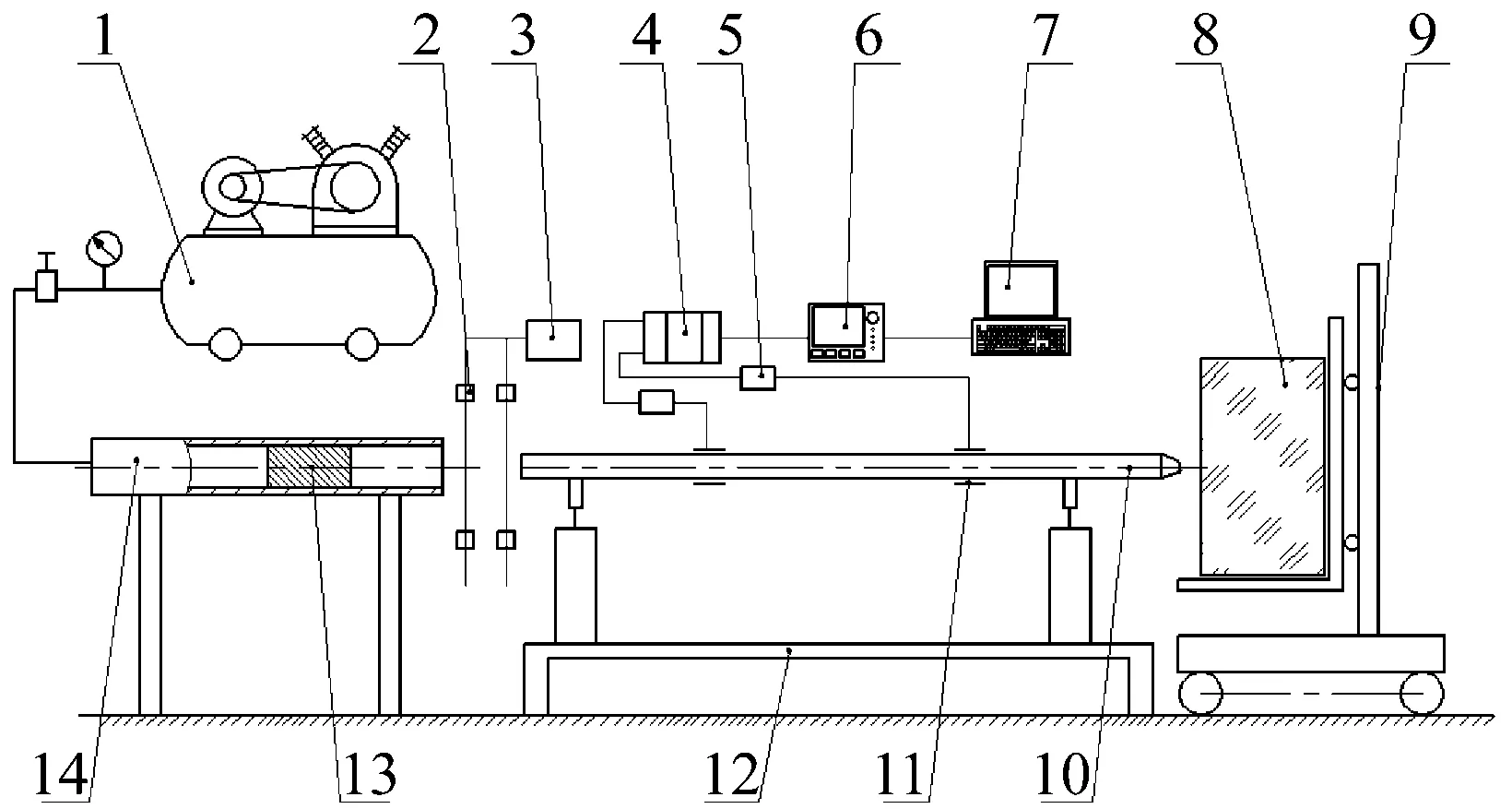
图2 高速冲击凿岩试验系统Fig.2 High speed percussion drilling test system

试验装置实物,如图3所示。试验中钎杆的冲击端面以及钎杆中部都粘贴有电阻应变计，如图3(b)所示，以此检测钎杆相应位置处的应变，所测得的信号反馈入动态应变仪放大后，与测速仪的数据信号一起进入数据采集系统，系统高速采样后，进入微机完成数据的处理、存储以及输出等。

试验中微机输出信号为电压信号U0，应变片桥路连接为半桥形式，通过公式换算可求得钎杆应变与采集到的电压信号U0之间的关系式为

式中:k为应变片灵敏度;U为供桥电压。试验中应变片的灵敏度系数为2.17，供桥电压为6 V。

1.空压机;2.激光探头;3.测速仪;4.应变放大器;5.桥盒;6.示波器;7.电脑;8.岩石;9.手动填高叉车;10.钎杆;11.应变片;12.测试台架;13.冲击活塞;14.压气枪管。

(a)

通过应变即可求出钎杆对应截面的应力。试验中测量钎杆距离冲击端面950 mm处的应力，理论计算可获得相同截面位置处钎杆应力时间历程曲线。试验数据与理论计算仿真结果对比,如图4所示。

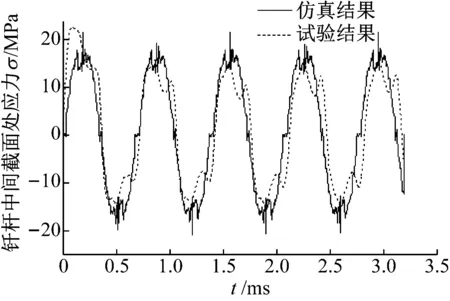
图4 试验结果与仿真计算结果对比Fig.4 Comparison of test and simulation

比较可知，试验值与理论仿真结果随时间的变化趋势一致，峰值应力出现的时刻与幅值也基本相同，从而验证了理论模型的准确性。误差产生的主要原因是实测钎杆截面形状为六边形，而非理论圆形，理论计算时需将其面积等效换算为实心钎杆面积计算。

2.2 钎杆直径对冲击过程动力响应的影响

考虑钎杆截面变化对冲击过程动力响应的影响，凿岩机各冲击部件计算参数,如表1所示。不同钎杆直径下，钎杆距离撞击接触面950 mm位置处钎杆截面轴力时间响应曲线,如图5所示。

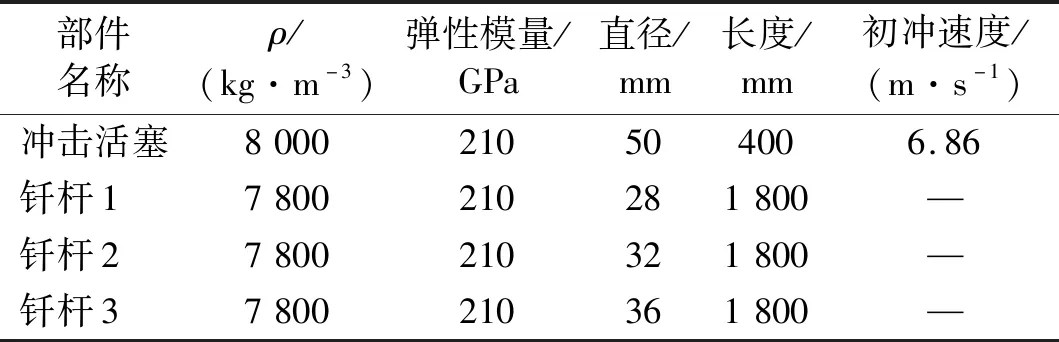
表1 不同钎杆直径下的计算参数Tab.1 Calculation parameters of different drill rod diameters

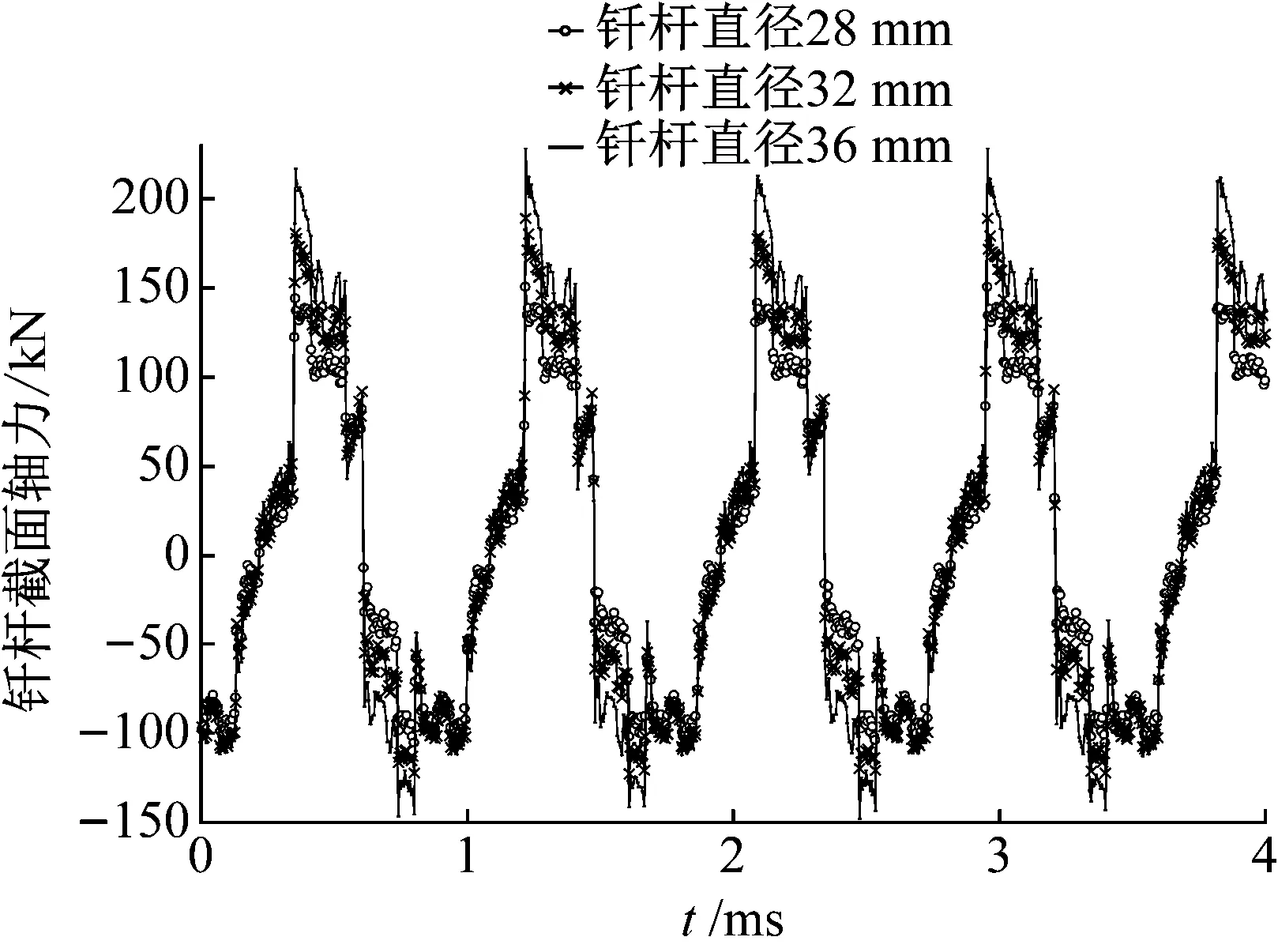
图5 不同直径下钎杆950 mm位置处截面轴力响应Fig.5 Axial force response of section at 950 mm of drill rod with different diameters

由图5可知：钎杆截面轴力呈周期性变化，该变化是应力波在杆中传播所致。应力波从撞击接触面向钎杆右端面传播，在到达右端面后发生反射，由于钎杆左右两端面均为自由端，所以，应力波在端面反射后，反射波和入射波大小均相等且方向相反，因此杆中应力波呈现周期性变化。此外，不同杆径钎杆的应力变化周期以及变化趋势相同。这是由于应力波传播速度仅与材料密度及弹性模量相关，在材质和长度不变时，杆件中应力波传递时间不发生变化，撞击力变化的时间历程也不改变。随着钎杆直径变大，钎杆中相同截面处轴力幅值升高。这是因为，材料的波阻与其弹性模量、密度以及截面积相关。钎杆直径变化会直接影响其自身波阻，进一步影响应力波透射率。所以撞击过程中，通过透射传播到钎杆中的应力波幅值也会随截面积变化。钎杆直径增加会导致钎杆截面轴力的增加，这样凿岩机的破碎能力也将随之增强。

不同钎杆直径下，冲击过程结束后，活塞接触面的v-T历程曲线,如图6所示。冲击分离过程中，活塞各截面速度是活塞作为刚体的自由飞行速度和应力波在活塞中传播引起的各截面运动速度的叠加，所以分离过程中活塞冲击接触面的速度将以活塞刚体运动速度为基础上下波动。随着钎杆直径的增大，分离后冲击活塞的刚体运动速度(即反弹速度)增大，且速度波动幅值增加，即应力波幅值增加。

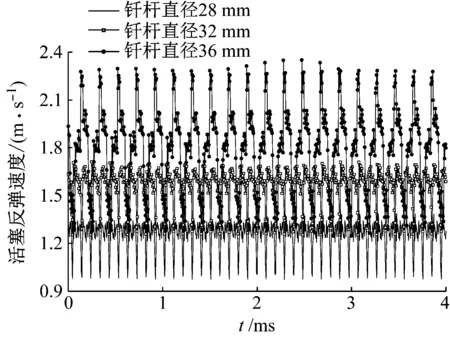
图6 不同钎杆直径下冲击活塞撞击面速度响应Fig.6 Velocity response of impingement surface of impact piston under different bit diameters

不同钎杆直径下，冲击结束后钎杆所获动能占活塞初始总动能的百分比,如图7所示。由图7可知:钎杆中动能呈现周期性变化，当钎杆直径不同时，活塞能量利用率曲线变化趋势基本相同。这是因为冲击过程结束后，钎杆获得的总能量中部分为动能，部分为弹性势能，应力波在钎杆中的周期性传播使得钎杆中动能和势能周期性的相互转化。在活塞直径大于钎杆直径的情况下，随着钎杆直径增大，活塞能量利用率将随之升高。在常用工程结构参数许可的范围内，应尽可能使钎杆的直径接近冲击活塞直径，以而减少应力波损失。

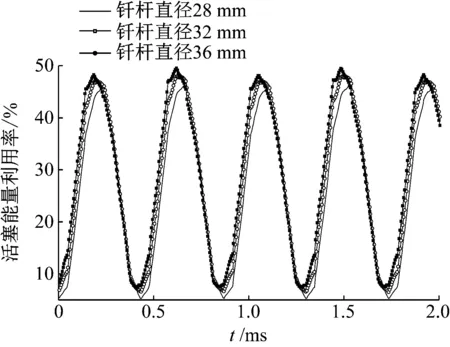
图7 不同钎杆直径下冲击活塞能量利用率Fig.7 Energy utilization of impact piston under different impact piston diameters

2.3 钎杆长度对于冲击过程动力响应的影响

同一活塞冲击速度，在不同钎杆长度条件下，各冲击部件计算参数,如表2所示。分离过程中钎杆截面轴力时间历程曲线,如图8所示。

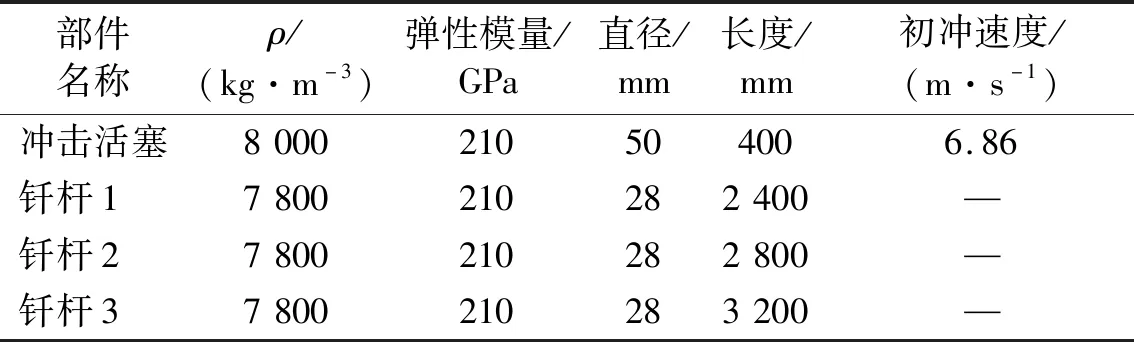
表2 不同钎杆长度下的计算参数Tab.2 Parameters of different drill rod length

在钎杆材料密度不变时，随钎杆长度的增加，则应力波的传播周期变长，所以钎杆截面轴力变化周期也延长。此外，当钎杆长度变化时各钎杆截面轴力大小基本相等(见图8)。由于钎杆截面积相同，所以应力波引起的钎杆截面应力相同。钎杆截面应力与杆中的应力波大小有关，说明钎杆长度的变化对分离过程中的钎杆应力波的影响不大。

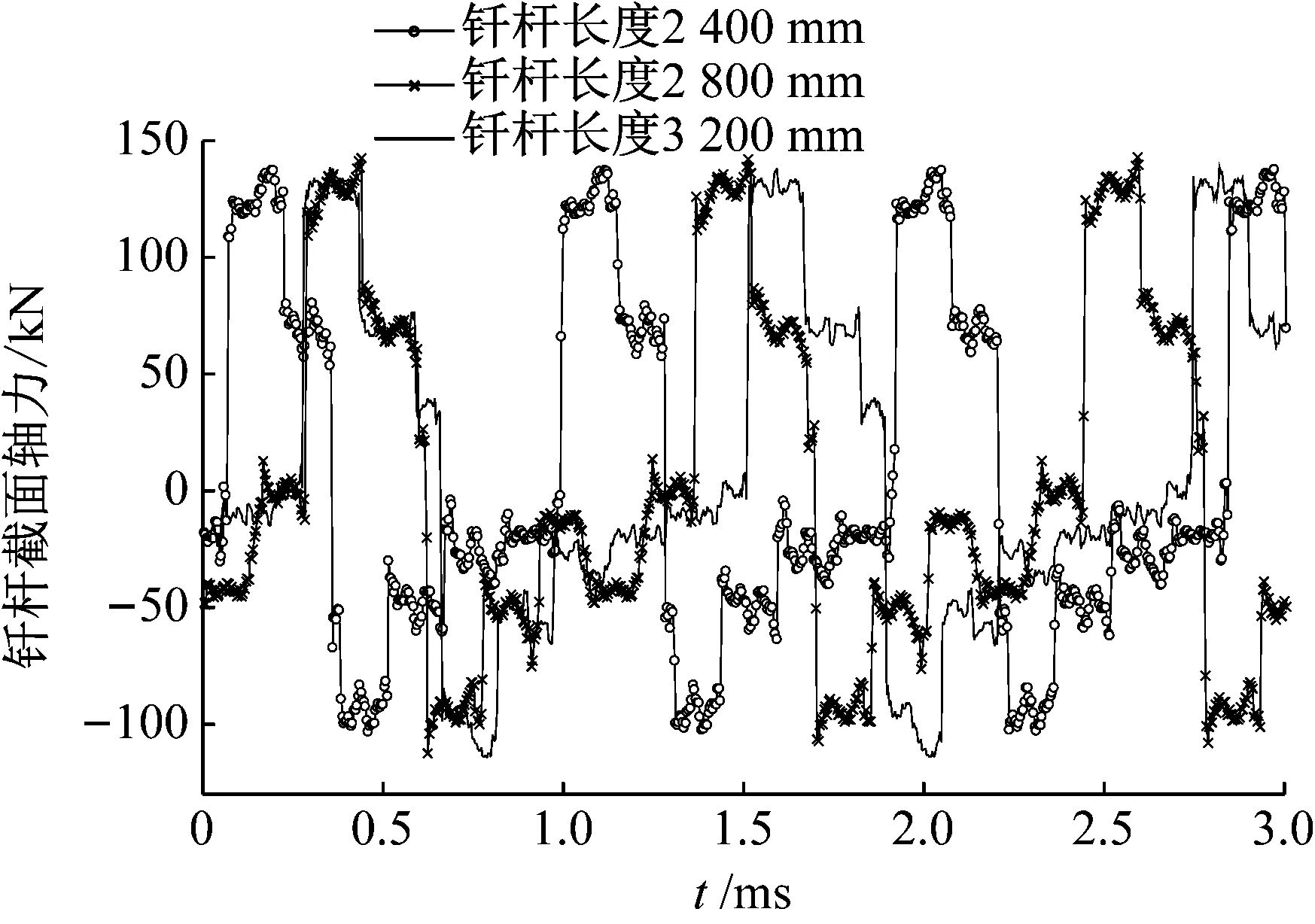
图8 钎杆长度不同时截面轴力Fig.8 Axial force of section at different lengths of drill rod

当钎杆长度变化时，冲击过程结束后钎杆截面速度的响应曲线,如图9所示。

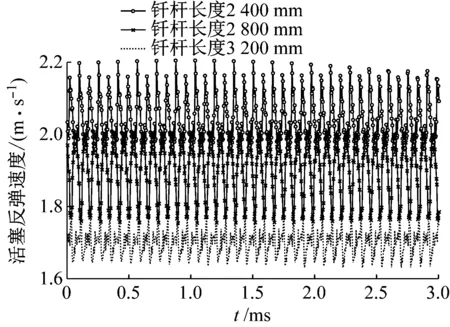
图9 钎杆长度变化时活塞撞击面速度响应曲线Fig.9 Velocity response curve of piston impact surface when the length of drill rod changes

由图9可知:随着钎杆长度的增加，冲击活塞的反弹速度将会降低。冲击分离后钎杆1、钎杆2和钎杆3对应的冲击活塞分别获得2.04 m/s、1.91 m/s、1.70 m/s的刚体运动速度。即随着钎杆长度的增加，冲击时将较多的碰撞能量传递给钎杆，而活塞中将残留较少的能量。在实际工作过程中因钎杆长度的变化，活塞也将产生不同的反弹速度，致凿岩机的冲击频率也会随之变化，凿岩机控制阀的工作频率及蓄能器容量须做适当调整，避免因反弹参数变化而出现困油或供油不足现象，以及避免由此引起破碎效率下降和密封结构破坏。

分离过程中活塞能量利用率曲线,如图10所示。3种钎杆长度情况下，能量利用率变化曲线均呈现周期性变化规律，且3种情况下变化周期不同，随着钎杆长度的增加，曲线变化周期延长，能量利用率升高，说明分离后钎杆具有较大的动能。

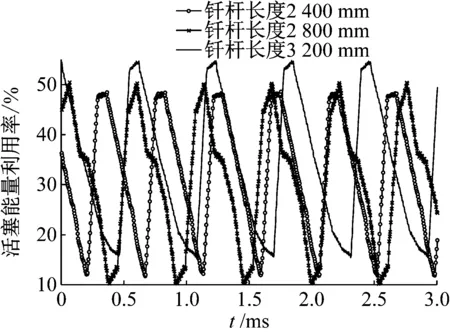
图10 钎杆长度变化时活塞能量利用率Fig.10 Piston energy utilization rate varying with length of rod

2.4 活塞初冲速度对于冲击动力响应的影响

同一活塞在不同初冲速度条件下，其各部件的计算参数,如表3所示。

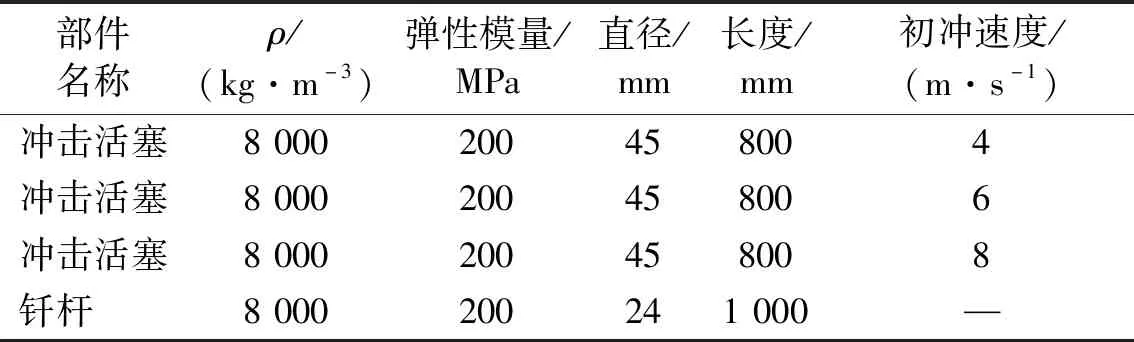
表3 活塞不同冲击初速度下计算参数Tab.3 Parameters of piston at different initial velocities

冲击活塞在不同初冲速度下，分离过程中钎杆截面轴力时间历程曲线,如图11所示。分析可知，随着活塞初冲速度增大，钎杆截面轴力相应增大。分离过程中钎杆截面轴力主要因应力波传播致杆件拉伸或压缩所产生，所以钎杆截面轴力越大说明应力波引起的杆件截面位移也越大，即钎杆中应力波的幅值越大，钎杆获得的弹性势能及动能也越高，越有利于钎杆完成破碎工作。所以，在被破碎物强度较高的场合可通过增大活塞初冲速度来实现破碎。

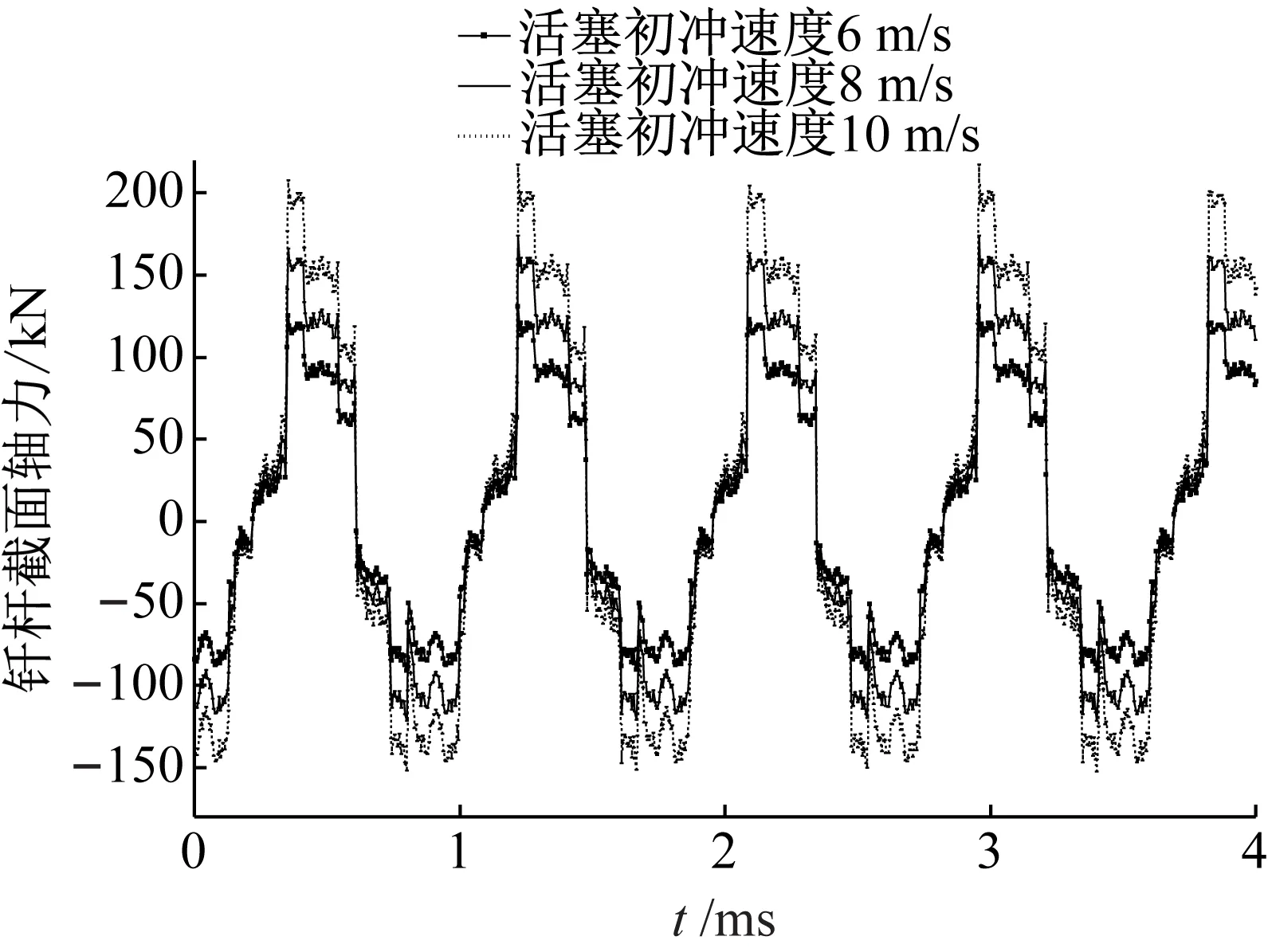
图11 不同活塞速度条件下钎杆截面轴力响应曲线Fig.11 Axial force curve of drill rod section under different piston velocities

不同活塞速度下，冲击活塞左侧边界撞击面的速度响应和能量利用率,如图12、图13所示。由图12、13可知：当活塞初冲速度分别为6 m/s、8 m/s以及10 m/s时，反弹过程中活塞截面速度分别在1.10 m/s、1.46 m/s以及1.83 m/s附近波动，即活塞反弹速度随活塞初冲速度的增加而增加，但活塞能量利用率基本不发生变化。

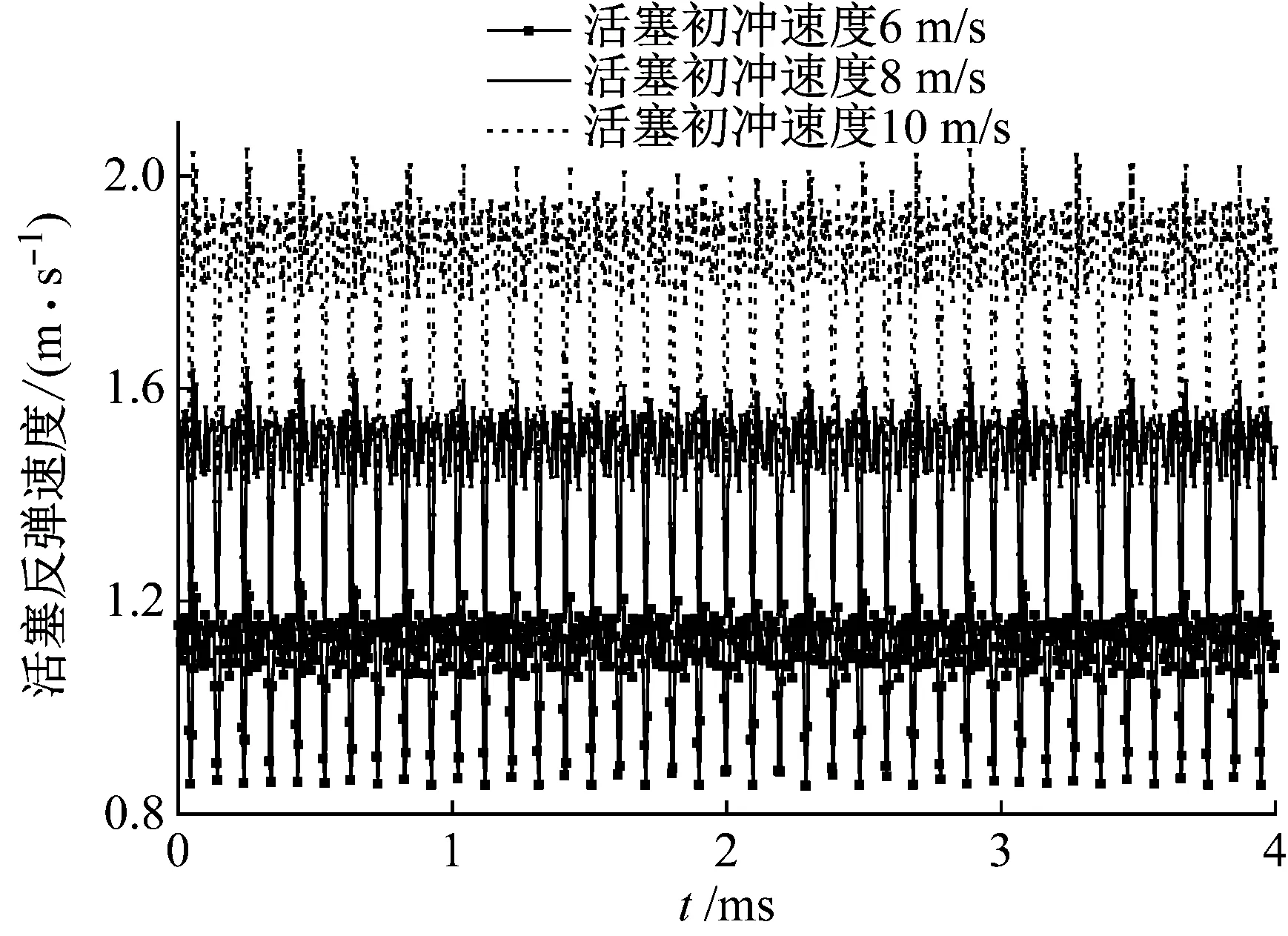
图12 不同活塞速度条件下活塞接触面速度响应曲线Fig.12 Speed response curve of piston contact surface with different piston velocity

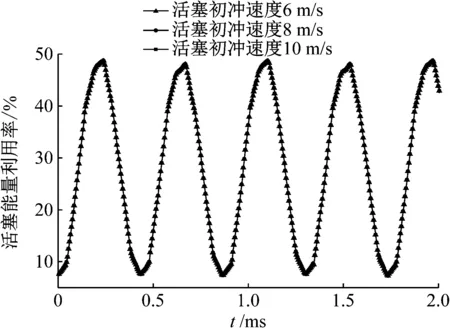
图13 不同初冲速度活塞能量利用率Fig.13 Energy utilization rates of different initial pistons charging speeds

3 冲击碰撞机理及冲击杆件瞬态应力波

以表4中的冲击状态来分析凿岩机工作中的冲击碰撞机理。通过理论计算可得冲击活塞及钎杆各截面在冲击碰撞过程中的应力波变化历程,如图14、图15所示。

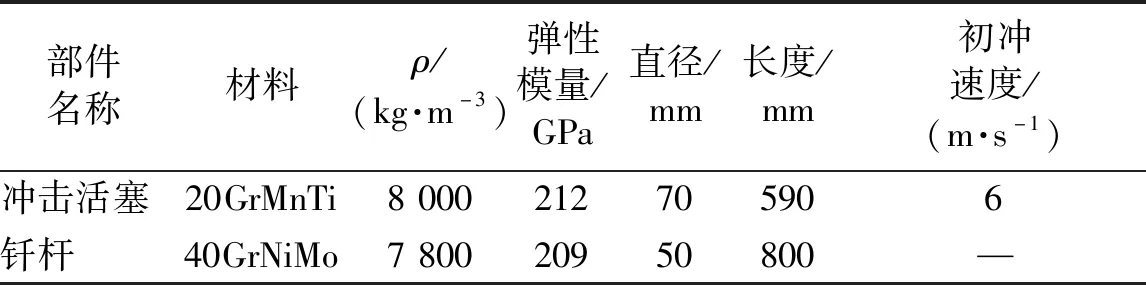
表4 冲击碰撞计算参数Tab.4 Calculation parameters of impact collision

由图14可知:冲击碰撞前，活塞所有横截面的应力值均为零。冲击碰撞发生后，应力波从活塞左端面开始传递。随时间变化，应力波传播使活塞各横截面均受压应力作用。当应力波传播到活塞右侧自由端时，形成反射波并实现反射率为1的反向传递。应力波在反射过程中又与原入射波矢量叠加，所以反射波传递到的横截面应力值恢复为零。当反射波传递到活塞-钎杆接触面时，钎杆中应力波还未传递到碰撞接触面，其间活塞中应力保持为零。而当钎杆中的入射波和反射波叠加后的应力波传播到碰撞接触面时，又将通过透射和反射作用分别在活塞及钎杆中继续传播。碰撞过程中，活塞右端面应力值始终为零，其左端面始终受压应力作用。

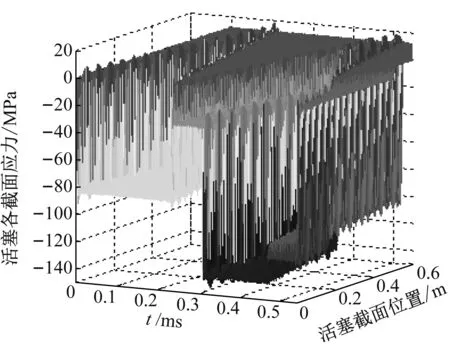
图14 冲击活塞各横截面应力时程曲线Fig.14 Section’s stress time histories of the impact piston

图15为冲击碰撞过程中钎杆各截面应力时程曲线图。初始时，钎杆各横截面应力为零，冲击碰撞发生后，应力波从碰撞接触面处向左传播，应力波传播到的位置钎杆截面逐渐受压应力作用。当应力波传播到钎杆固定端面，通过反射作用将反向传播。由于钎杆左端面存在高波阻的凿岩介质，所以从凿岩界面反射到钎杆中的应力波与杆件中原有应力波叠加后应力幅值变为原来的两倍。由图15可知，整个冲击碰撞过程中，钎杆固定端处所受的应力幅值最大。

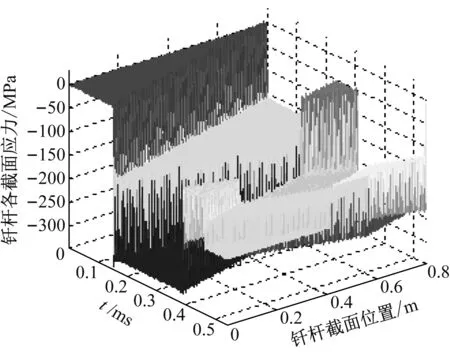
图15 钎杆各截面应力时程曲线Fig.15 Section’s stress time histories of drill rod

通过对上述冲击部件截面瞬态应力波传播分析可获得凿岩机工作过程撞击机理[18]。

4 结 论

(1)在冲击活塞直径和初冲速度不变情况下，钎杆直径变大，钎杆对应截面处轴力增大，致钎杆撞击破碎能力增强，但冲击能量利用率将有所降低。同时，若钎杆直径逐渐减小，则冲击活塞的反弹速度将逐渐降低，当反弹速度小于零时，将会发生活塞与钎杆的二次碰撞。

(2)活塞冲击速度影响截面撞击应力幅值的变化，两者间成一定比例关系，但冲击速度对冲击应力的时间历程影响不大。当冲击活塞为高初冲速度时具备较高能量，将使得冲击过程中接触面的撞击力及应力幅值增大，可使得凿岩机具的破碎能力得到迅速提升。同时，撞击后，冲击活塞的反弹速度也会随之增大，即残留在冲击活塞中的动能较高，冲击能量的利用率较低。