考虑载荷与网损均匀性的配电网拓扑多目标规划

王楠，李省，杨小龙，高帆帆，钟嘉庆，贾清泉

（1. 国网冀北电力有限公司智能配电网中心，河北省 秦皇岛市 066100；2. 河北建投沙河发电有限责任公司，河北省邢台市 054000；3. 河北省电力电子节能与传动控制重点实验室（燕山大学），河北省 秦皇岛市 066004）

0 引言

配电网规划本质上是一个动态优化网络架构的问题[1-2]。现阶段针对配电网中分布式电源均匀优化的研究已较为成熟[3-4]，许多学者将重心放在配电网网络拓扑结构的研究上，合理的网架结构规划，不仅可以降低网损、改善电能质量，还能够提高系统的可靠性[5]。因此配电网拓扑结构的科学合理规划对配电网的未来发展具有重要意义。

配电网网络拓扑结构的研究主要包括运行风险研究[6]、协调优化研究[7]、网架结构优化[8]等方面。在网架结构优化中，配电网拓扑结构约束和重构求解方法是配电网网架重构的主要技术难点。文献[9]对拓扑结构约束，结合图论与辐射状拓扑条件，提出一种主动配电网复杂网络拓扑判别方法；文献[10]对配电网结构进行优化，提出计及分布式电源动态行为的配电网重构概率约束优化策略和求解方法，构建了配电系统动态重构的数学模型；文献[11]研究表明了电力系统运行工况下的自组织临界状态与其电网结构的均匀程度密切相关，并提出网络拓扑熵的概念用以衡量电网结构的均匀程度；文献[12]从拓扑结构、可靠性、经济性3 个方面建立多属性评价指标体系，分析了不同地区差异化需求下所适合建设的最优网架。

然而在配电网重构中，随着系统网架结构的改变，其均匀性也会发生改变，进而对系统的网损和可靠性产生影响[13]。配电线路分布的均匀性指配电网络拓扑结构的均匀程度，它反映了在电源确定的状况下配电网网架结构中各线路负荷的分布情况。配电网网架结构均匀性差，一种情况是指线路轻载，利用率较低，另一种情况是指线路重载，甚至出现输电阻塞现象，使配电网可靠性降低。因此在配电网规划中提高网络拓扑结构均匀性是提高配电系统可靠运行的重要措施。

目前对配电线路分布均匀性的研究主要集中在线路传输均匀度与输电能力的相关性方面。文献[14]分析了配电线路均匀性，以及它与系统安全性和可靠性的关系，综述了电网规划中需要考虑的均匀性问题、评价指标和优化方法，指出了现有研究中存在的一些问题；文献[15]根据电力系统配电线路的节点分布进行配电的自动控制和均衡分配，进行电力系统配电线路的连锁故障自动检测和修复。配电线路分布的均匀性广泛应用在电网规划中。文献[16]提出了一种配电网负荷均衡重构的方法，针对负荷动态特性建立了馈线过载量化模型，通过重过载馈线及其各邻接馈线联络开关、分段开关的状态调整，确定最优的馈线负荷均衡方案；文献[17-18]也在电网规划中考虑了配电线路负荷分布的均匀性，其方法是在传统电网规划模型基础上加入线路负载率标准差最小的目标函数，同时考虑电网规划经济性与均匀性的多目标优化模型。然而上述文章在均匀性中考虑的特征指标缺乏完整性，不利于对配电网拓扑特征均匀性进行全面、科学地评估，从而影响规划的可靠性。

本文针对上述问题，提出综合考虑配电线路荷载率和网损率的方法，多角度分析影响配电网拓扑结构均匀性的因素，定义荷载率拓扑熵和网损率拓扑熵的加权和为配电网拓扑结构均匀分布系数指标。最后，建立配电网多目标规划模型进行优化计算，以提高配电网规划的经济性及可靠性。

1 配电线路均匀分布系数

针对配电网线路分支较多、负荷密度较大、运行可靠性要求较高的特点，在配电网规划中需要考虑配电线路载荷、配电线路网损等影响网架结构均匀性的因素，从而使配电网网架结构更合理，提高运行的可靠性。本文中定义的配电线均匀性是指在投入运行时各条线路上的载荷率分布和网损率分布的均匀程度，载荷率和网损率的均匀程度越高，则表明配电线均匀性越好。

信息熵是系统无序程度的一个度量，对于某项指标，可以用熵值来判断该指标的离散程度，其信息熵值越大，指标的离散程度越小，指标越稳定[19]。

本文定义配电线路荷载率拓扑熵、网损率拓扑熵来表征配电线路的荷载率和网损率的分布情况，并将 2 者的加权和定义为配电网的均匀分布系数，再以均匀分布系数最大为目标函数进行优化计算，目的是为了使配电网线路荷载率和网损率分布更加均匀，提高配电网网络拓扑结构的均匀性。

本文定义配电线路均匀分布系数为荷载率拓扑熵和网损率拓扑熵的加权和，即

式中：W是配电线路均匀分布系数； λ1、 λ2分别是荷载率拓扑熵s1和网损率拓扑熵s2的权重。

1.1 荷载率拓扑熵

配电网线路荷载率表征了配电线路承载负荷的能力，各条线路上荷载率分布差异较大，会导致配电网承载负荷的能力不均匀，容易给电网带来安全性问题，若各条线路上荷载率分布接近相同，则配电网承载负荷的能力较均匀，能较好地满足未来负荷增长，减少安全性问题的出现[20]。

配电线路i的荷载率Hi为

1.2 网损率拓扑熵

以上分析可知，配电线路均匀分布系数即荷载率拓扑熵和网损率拓扑熵越大，说明配电线路荷载率和网损率的分布越均匀，表明网络拓扑结构较均匀，因此在一定程度上可减少支路故障或停电事故发生的概率。

2 配电网多目标规划模型

2.1 目标函数

2.1.1 经济性目标函数

在配电网规划中，考虑经济性，以全社会年综合成本最小为目标，其包括配电网投资成本、配电网运行成本、阻塞补偿成本，可表示为

式中：C1为配电网投资成本；C2为配电网运行成本；C3为配电网阻塞成本。

1）配电网投资成本。

在配电网规划中，根据单条线路使用年限和贴现率，将配电网新建线路投资成本换算成等年值成本，表示为

2）配电网运行成本。

配电网在规划期内需要考虑运行成本，主要包括所有线路的年运行维护成本，通常将年运行成本表示为一定比例的配电网投资成本，具体表示为

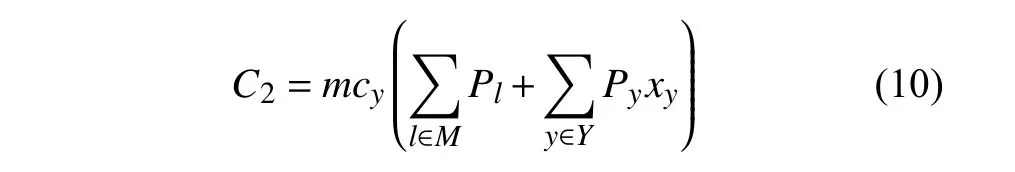
式中：M是原有线路集合；Pl是原有线路集合中第l条线路的容量；m是线路的运行维护成本系数，一般取值为1%～2%，本文取1.8%。

3）配电网阻塞成本。

配电阻塞多由负荷需求超过线路容量造成，当发生配电阻塞时，配电网应当给予电厂(发电商)一定的补偿费用，故考虑配电阻塞成本。

电网中a−b支 路的阻塞成本可表示为

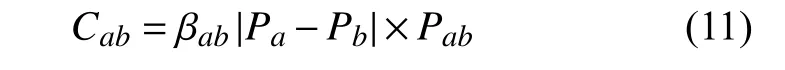
式中：Pa、Pb分别为a、b节点的节点电价；Pab为a−b支路容量； βab为线路a−b是否发生阻塞的状态变量，βab=1时线路a−b发生了输电阻塞，βab=0时线路a−b未发生阻塞。

2.1.2 均匀分布系数目标函数

本文以最大均匀分布系数作为目标函数，通过合理规划配电网路径来提高配电网网架结构的均匀性，表示为：

2.2 约束条件

本文综合考虑了配电网的全社会经济成本和网架结构的均匀性，故配电网的规划需要满足以下约束条件：

1）配电网规划投资成本约束。

在整个规划期内要求新建输电线路总投资成本不超过其上限，即

5）节点功率平衡约束。

配电网中节点注入功率和负荷需求的功率等于支路上的消耗功率，即

2.3 求解算法

本文采用多目标细菌群体趋药（bacterial colony chemotaxis，BCC）算法对规划模型进行求解，BCC 算法是一种受自然界生物行为机制的启发而得到的新的优化算法。这种算法模拟细菌在化学引诱剂环境中的运动行为来进行函数优化。该算法具有收敛快、精度高，能全局搜索等优点。目前已有许多学者对该算法进行研究，并在电力系统无功优化[21]、电力系统暂态稳定评估[22]等方面取得了较好的成果。本文研究的问题是经济成本最小及均匀分布系数最大，属于多目标范畴，该方法适用于解决本文目标函数，而且本文多目标规划属于离散化问题，因此采用离散细菌群体趋药性（ discrete bacterial colony chemotaxis，DBCC）算法对其进行优化。

首先设定细菌的初始位置，并设定细菌的转移速度v，通常将其设定为不变值，取值为v=1。其次设定基本参数：确定初始精度βbegin、最终精度βend和更新常数 β。然后初始化细菌群体，因为在整个规划年限里不同时间段，配电线的投建情况不一样，因此把配电线的建设情况离散化，1表示相应配电线进行建设；0 表示相应配电线不建设，如图1 所示。图1 中的z和Z表示某一个规划年和规划周期。

图1 编码形式Fig. 1 Coding form

本文利用该算法求解模型，得到帕累托解集，并应用文献[23]中的折中解方法选择最优方案。

3 算例分析

3.1 基本参数

本文以IEEE33 配电系统为算例进行仿真验证。IEEE33 配电系统图以及节点编号如图2所示。

图2 IEEE33 配电系统的节点编号Fig. 2 Nodal serial number of IEEE 33 bus distribution system

该配电网共33 个节点，32 条线路，其基准电压为12.66 kV，基准容量为10 MVA，总负荷为3715+ j2340 kVA，候选线路共32 条，基本数据参数见附录表A1。本文设定规划期为5 年，折现率为 0.05。新建线路投资总额上限为40 万元。

3.2 仿真结果分析

为证明本文模型的有效性和合理性，考虑配电网的经济成本和网络拓扑结构的均匀性，将本文模型与单目标模型进行对比分析，令模型1 为本文模型，模型2 为仅考虑配电网全社会经济成本的配电网单目标规划模型，模型3 为仅考虑荷载率拓扑熵和网损率拓扑熵，而不考虑全社会经济成本的配电网多目标规划模型，3 种模型新建输电线路计算结果如表1 所示，3 种模型各成本和相关指标如表2 所示。

从表1 中可以看出，本文模型（模型1）新建了11 条线路，模型2 新建了15 条线路，比模型1 多投建了4 条，模型3 新建17 条线路，比模型1 多建6 条。从表2 中可以看出，模型1 的线路投资成本较模型2 和模型3 小，从而运行成本也较模型2 和模型3 小。

表1 各模型新建输电线路规划结果Table 1 Planning results of newly-built transmission lines in each model

表2 各模型的各种成本和相关指标Table 2 Cost and related indices of each model

在配电阻塞成本方面，模型2 的阻塞成本比模型1 的大得多，原因是模型1 提出了均匀分布系数的概念，综合考虑了配电网的网络拓扑结构，使得配电网的网架结构更加均匀，所以在规划时引起配电阻塞的可能性小，故阻塞成本比单目标规划模型的阻塞成本低。因此，在全社会总经济成本上，模型1 的经济性较模型2 好。由于模型3 不考虑配电网的经济性，故在投建线路上比模型1 多，相应的全社会总成本比模型1 高。因为模型3 未考虑均匀分布系数，所以在配电网网络结构的均匀方面较模型1 差，从而验证了本文模型合理性。

以上研究结果表明，本文提出的均匀分布系数可有效提高载荷和网损分布的均匀性，使得配电网在运行中更加可靠稳定。同时在经济成本中考虑配电网阻塞成本，通过模型对比，可验证本文所提模型能够有效降低阻塞成本，提高电网经济性，对配电线均匀性的研究起支撑作用。

本文截取20 条配电线路，将3 个模型的荷载率和网损率进行对比，对比结果如图3—4 所示。

图3 不同模型荷载率分布对比结果Fig. 3 Comparison results of load rate distribution of different models

从图3 和图4 对比结果中可以得出，模型1的荷载率和网损率的分布曲线比模型2 和模型3平缓，原因是模型1 的配电网规划模型是考虑均匀分布系数的多目标规划模型，从而使得配电网的拓扑结构均匀性更好，故配电线路上的荷载率和网损率分布较均匀，而模型2 仅考虑了经济性，既投建了大量的线路，又忽略了配电线路的荷载率和网损率的均匀分布。模型3 未考虑均匀分布系数，导致荷载率拓扑熵和网损率拓扑熵小，即配电线路上荷载率和网损率分布不均匀，进而反映出模型1 的网络拓扑结构更加均匀。综上所述，本文基于均匀分布系数的配电网网络拓扑结构的规划模型更具有效性。

图4 不同模型网损率分布对比结果Fig. 4 Comparison results of network loss rate distribution of different models

4 结论

本文综合考虑配电网经济性和网架拓扑结构的均匀性，提出基于均匀分布系数的配电网网络拓扑结构多目标规划模型，并采用多目标BCC算法对模型进行仿真，算例仿真结果表明：

1）与仅考虑经济性的单目标模型进行对比，本文所提模型能降低配电阻塞成本和全社会经济成本。

2）与不考虑均匀分布系数的配电网规划模型对比，本文模型能有效增加网络拓扑结构的均匀性，提高系统可靠性。

（本刊附录请见网络版，印刷版略）