某炮塔结构轻量化计算效率提升研究

葛尧，陈龙淼，徐树威，谭建辉

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.建华机械有限公司试验场，黑龙江 齐齐哈尔 160006；3.重庆望江工业有限公司，重庆 400071)

炮塔作为火炮的重要部件，其结构减重有利于提高火炮装备的机动性和适装性，但是减重可能会影响炮塔结构的刚强度及动态特性，进而影响火炮的射击精度。随着结构优化理论和计算机技术的发展，使炮塔在满足一定设计约束条件下实现结构的最优化成为了可能[1]，炮塔的优化设计对提高火炮的性能有重要的意义。

对炮塔结构的轻量优化设计已经存在较多研究[1-5]，研究者针对各炮塔结构特点，选取不同的优化工具进行了轻量化工作。葛建立等[4]基于有限元网格模型及静态刚强度分析结果，使用了Hyperwork软件自带的优化模块进行了炮塔结构优化。基于有限元网格模型，杜春江等[5]基于多岛遗传算法对炮塔体结构进行了优化设计，并对比分析了优化前后炮塔体结构在典型工况下的动态响应特性。针对越来越复杂的优化问题，许多研究人员开始使用基于融合或组合不同的优化算法来提高解决复杂问题的计算效率，并在实际工程中部分应用了这些组合优化算法[6-10]。甄春博等[9]使用了存档微遗传算法和Hooke-jeeves直接搜索法组成的组合优化算法，对碟形水下滑翔机结构进行了优化；LI等[10]使用遗传算法和模拟退火方法的融合优化算法，对箱型零件的工艺流程进行了优化。

上述研究成果针对火炮及炮塔展开了优化研究，为火炮优化方面的问题提供了重要参考。但对于小口径火炮而言，由于其射击频率较高，炮塔结构的固有频率有可能与射击载荷的频率范围重叠，发生共振，严重影响射击精度和炮塔内设备的正常运行，因此优化中需要考虑最低固有频率的约束，防止最低固有频率进入危险范围；在优化求解方面，直接使用有限元网格模型进行优化计算效率较低，迭代次数较多会导致需要的时间较长，而迭代次数过少则会导致优化结果不理想；炮塔结构设计变量较多，设计空间维数较高，单一常规优化方法可能导致优化结果陷入局部最优困境。能避免局部最优困境的模拟退火算法、遗传算法、粒子群算法等全局优化算法，无法在相对最优解的局部空间进行精确搜索，只能得到全局相对最优解，难以获得真正的全局最优解。

笔者通过使用拉丁超立方方法进行实验设计，利用得到的样本数据建立起设计变量与结构最低固有频率之间的BP神经网络代理模型，并通过均方误差MSE和决定系数R2衡量代理模型精度。随后，针对传统数值优化方法容易陷入局部最优解且全局优化算法搜索时间过长的问题，使用改进多岛遗传算法和非线性二次规划算法的组合优化算法进行优化，得到了优化结果。

1 炮塔模态特点及优化要素确定

1.1 炮塔模态特点分析

基于某小口径速射火炮炮塔参数化三维实体模型，构建炮塔有限元模型，炮塔外罩及加强筋板采用壳单元进行离散；其余部分采用实体单元进行离散。炮塔结构如图1所示，有限元离散模型如图2所示。炮塔主要材料为铝，摇架部分材料为钢，材料属性如表1所示。

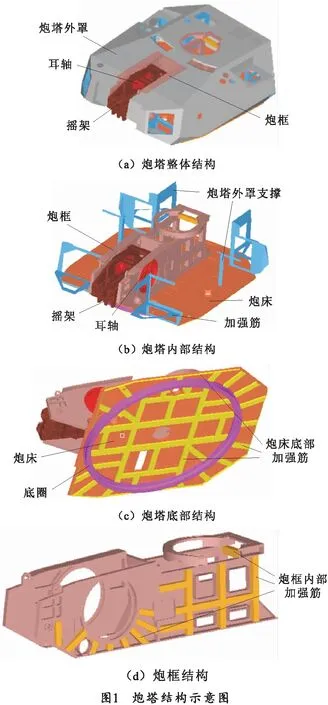
表1 材料属性

将炮身及反后坐装置、炮塔内部各箱体、外挂装甲及其他与结构关系较小的质量体简化为质量点，并与安装位置建立连接关系，如图3所示。

参考炮塔的实际工作情况，在底部座圈建立六自由度的固定约束。利用动力学模型得到如图4所示的火炮发射过程中的单次射击后坐阻力曲线，并施加于炮身及反后坐装置的简化质心位置。

通过模态分析可知，炮塔结构的最低固有频率为32.680 Hz，第1、2阶模态特征为炮塔沿x轴方向的整体扭转，第3、5阶模态特征为炮塔后部沿y轴方向的扭转，第4阶模态特征为炮塔沿x、y轴方向的混合扭转，第6阶模态特征为炮塔左侧沿y轴方向振动。

1.2 设计优化要素的确定

笔者以炮塔有限元仿真结果为基础，对炮塔结构进行优化设计。由于耳轴、摇架、炮框、炮床及座圈部分的尺寸结构与炮塔其他设备的安装相关性强，在炮塔总体方案已经确定的情况下，对这部分结构进行优化所涉及的因素较多，优化工作较为复杂，且无法保证优化结果的工艺性,因此，选择炮塔外罩、炮床底部加强筋、炮框内部加强筋、炮塔外罩支撑加强筋4个部分进行尺寸优化。

通过动力学仿真结果可知，动力学过程中最大位移为78.91 μm，相对较小；加载过程中的最大应力为30.08 MPa，远小于许用强度，且集中于非优化部分的应力集中处，对优化模型所考虑的筋板结构尺寸变量不敏感。参考相关文献，优化模型建立过程中不考虑刚强度问题，在最后使用有限元模型对优化结果的刚强度进行计算校验作为补充[3]。

为了便于优化分析，定义x1为炮床底部通常加强筋厚度，x2为炮床底部中央加强筋厚度，x3为炮床底部环绕加强筋厚度，x4为炮床内部加强筋厚度，x5为炮塔外罩厚度，x6为炮塔外罩支撑加强筋厚度，如表2所示。

表2 优化设计变量

炮塔优化设计以结构质量最小为优化目标函数，以最低固有频率、计算精度为约束条件，其数学模型可表示如下：

(1)

式中：ω为炮塔各筋板结构质量；f为炮塔最低阶固有频率；f1为频率变量许用值。

某小口径速射火炮最大射速为150 发/min，其周期性射击载荷的频谱分析如图5所示，可以看出，射击载荷的频率主要分布于0～30 Hz。参考有限元仿真结果并考虑相关情况，f1取32 Hz。

2 炮塔结构优化设计

2.1 BP神经网络代理模型构建

优化设计的寻优过程中需要进行多次迭代，不断进行有限元仿真，耗时极长。笔者采用拉丁超立方方法取得样本数据[11]，并建立预测炮塔整体结构频率的BP神经网络代理模型。

利用联合仿真平台和有限元仿真软件进行设计实验，共取得190组实验样本数据。BP神经网络模型隐含层选取tansig为传递函数，输出层选取purelin为传递函数，选取trainbr函数为训练样本进行训练，输入层参数为6个设计变量，输出层参数为炮塔结构系统最低固有频率。得到输出函数Y与输入函数X之间的关系为[12]

(2)

式中：ωij为输入层到隐含层的网络连接权值；vj为隐含层到输出层的网络连接权值；bj为隐含层的阈值；bθ为输出层的阈值；φ(·)为隐含层的传递函数；ψ(·)为输出层的传递函数。

选取均方误差MSE与R2作为神经网络模型拟合效果的衡量标准。如图6、7所示，经过825次训练后，对于训练样本数据而言，均方误差达到了0.000 08，R2达到了1；对于测试样本而言，均方误差达到了0.074 38，R2达到了0.997 2，全部样本的R2为0.999 7。均方误差均小于0.1，且R2均大于0.99，可以认为BP神经网络代理模型的实际输出接近期望输出，网络拟合效果较为理想。

2.2 基于组合算法的多变量优化设计

在本文中，优化问题可以被描述为

(3)

该优化问题包括7个变量，是典型的多维设计空间问题。较高的维数易造成搜索最优值上的困难。笔者采用由改进多岛遗传算法与非线性二次规划算法(NLPQL)的组合优化算法解决该问题。首先通过改进多岛遗传算法在设计空间全局范围内寻找初步最优解，随后利用NLPQL算法在上述最优解附近进行局部精确搜索，确保解的最优性。

2.2.1 改进多岛遗传算法

多岛遗传算法[13-15]是从传统遗传算法基础上发展而来的一种算法。该算法将整个进化群体划分为若干子群体，将其称为“岛屿”，并在每个岛屿上对子群体独立地进行选择、交叉、变异等操作，如图8所示，图中k为整数，mi为迁移间隔。

多岛遗传算法选择浮点编码方式，个体的每个基因值用某一范围内的一个浮点数来表示，而个体的编码长度等于其决策变量的个数。交叉和变异运算遵循公式：

(4)

(5)

在传统遗传算法中，Pc和Pm是固定的，合适的取值需要经过多次重复测试才能得到。为此，本文采用了一种可以根据优化问题进行自适应调整的Pc和Pm计算方法进行改进：

(6)

(7)

式中：favg为当前所有个体的平均适应度值；fmax为当前所有个体的最大适应度值；f′为进行交叉运算的两个个体的较大适应度值；f为进行变异运算的个体适应度值；Pcmax、Pcmin分别为最大和最小交叉概率；Pmmax、Pmmin分别为最大和最小突变概率，其中，Pcmax，Pcmin，Pmmax，Pmmin∈[0,1]。

2.2.2 非线性二次规划算法

NLPQL算法[16]是一种基于序列二次规划算法(SQP)发展而来的数值优化算法，基本思想是将目标函数以二阶拉氏方程展开，并把约束条件线性化，使问题转化为一个二次规划问题并进行求解。

对于以f(x)为优化目标，gi(x)、hi(x)为约束条件的一般约束最优化问题：

(8)

NLPQL算法会在当前点(xk,λk)处，构建如下二次规划子问题：

(9)

式中：i,j=1,2,…,n;Bk为使用变尺度法(BFGS)近似的Hessian矩阵W(xk,λk)。规定

Φ1(x,μ)=f(x)+

(10)

D(Φ1(xk,μ),dk)≤-(dk)TBkdk-

(11)

此时，NLPQL算法的步骤如下：

步骤1选取参数μ>0，δ>0，ε>0，取初始点x0∈Rn，初始对称矩阵B0，令k=0。

步骤2解二次规划子问题的解(dk,λk+1)，若dk满足‖dk‖≤ε,则算法停止，输出最优解xk；否则执行下一步。

步骤3确定ak∈[0,δ]，使不等式满足：

Φ1(xk+akdk,μ)≤Φ1(xk,μ)+

βakD(Φ1(xk,μ),dk),β∈(0,1)。

步骤4令xk+1=xk+akdk。

步骤5用BFGS公式修正Bk得到Bk+1，使得Bk+1对称正定，再令k=k+1，转向步骤2。

3 优化结果及分析

优化迭代历程如图9所示，可知使用组合优化算法进行优化时，首先使用改进多岛遗传算法进行全局寻优，保证全局最优性，随后使用NLPQL算法在多岛遗传算法全局寻优基础上，对局部搜索进行加速，收敛速度较快，优化目标快速收敛。通过两种算法的组合优化，最终得到全局最优解。优化结果最终质量为448.165 kg，比原始结构质量525.420 kg减少了77.255 kg，减少了14.70%。各设计变量的最终优化结果如表3所示。

表3 组合算法优化结果 mm

使用有限元模型对优化结果进行校验计算，得到的结果对比如表4所示。前六阶固有频率仅有轻微下降，炮塔结构在发射过程中的最大位移从78.91 μm上升至81.83 μm，最大应力从30.08 MPa上升至31.67 MPa，分布情况未发生明显改变，证明优化结果基本可信。

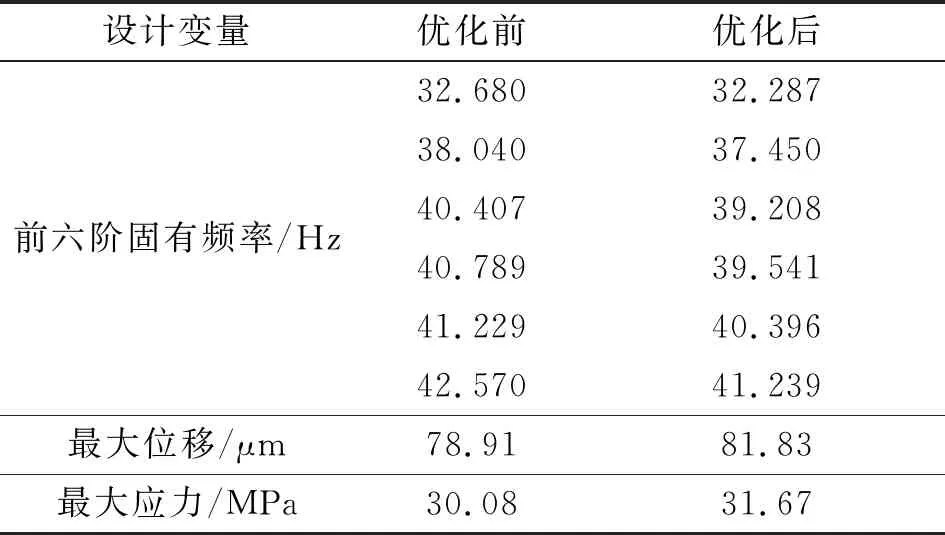
表4 结果对比

利用构建的BP神经网络代理模型，分别使用模拟多岛遗传算法(MIGA)、退火算法(ASA)、粒子群算法(PSO)对该优化问题进行求解，并与本文所述的组合算法(MIGA-NLPQL)进行对比，如表5所示。可以看出，在达到相同优化目标精度的前提下，组合算法的迭代次数较少，计算效率得到明显提高。

表5 优化算法对比

4 结论

笔者将有限元网格模型、代理模型、组合优化算法引入到某炮塔结构优化设计中，得出如下结论：

1)最终优化结果表明，在前六阶固有频率小幅下降，且刚强度变化较小的情况下，结构质量共减少了14.70%，减重效果明显。

2)对本文所述炮塔结构而言，使用BP神经网络构建代理模型能够在优化设计中提高计算效率，大量节省设计时间。

3)对于某炮塔结构优化问题，使用改进的自适应多岛遗传算法与非线性二次规划算法的组合算法进行计算，既能够使得遗传算法的全局搜索优势得到充分发挥，又能够避免其无法在局部优化空间内精确搜索的缺陷，迭代运算次数有明显下降，与其他传统优化算法相比计算效率有较大提升。