双排圆弧端齿连接结构对转子动力特性的影响
裘子剑 刘继兴
(①江苏联合职业技术学院无锡机电分院,江苏 无锡 214028;②北京航空航天大学能源与动力工程学院,北京 100191)
圆弧端齿最早由美国的格里森公司在二战时期设计研发,其目的是为了给活塞发动机曲轴(crankshaft)提供精确的连接[1]。由于圆弧端齿良好的自动定心精度及高承载能力,被广泛应用于航空发动机的转子连接结构中,如RB199、EJ200、MK202、RTM322等[2-3]。
Pisani S R分别采用有限元法和边界元法对圆弧端齿连接结构的应力集中系数进行了分析,研究表明采用有限元方法计算端齿类带多接触面的复杂结构,具有很好的适应性[4-5]。Honeywell的Muju S提出将圆弧端齿齿根倒角设计成多段复合结构,计算结构表明该结构能够显著降低齿根应力集中,提高端齿的疲劳寿命[6]。Yuan S等重点研究了重型燃气轮机中使用的端齿结构在不同载荷作用下的应力分布、拉杆松弛/失谐以及刚度分析[7],研究表明在工作转速下,由于端齿受离心力载荷作用,会出现转子拉杆松弛效应。Bannister R H首次采用有限元方法对端齿结构的刚度模型进行分析,提出用等效截面惯性矩参数进行定量描述端齿结构的弯曲刚度,并分析了端齿结构局部等效截面惯性矩与轴段截面惯性矩的关系对转子动力特性的影响[8]。Jiang X等针对重型燃气轮机的单排圆弧端齿连接结构,提出了考虑端齿结构细节的轴向压缩刚度模型[9],该模型采用有限元计算/实验方法得到关键位置处的变形参数,从而得到端齿的轴向压缩刚度。
对于转子系统连接结构对动力特性的影响研究,现有研究主要有套齿、螺栓、止口[10]等,对于套齿联轴器结构的研究,主要研究不对中、套齿啮合刚度、啮合力以及阻尼的影响。NASA的研究[11]采用非常简化的模型分析了套齿、止口定心面和端齿的阻尼特性,该模型能够简单分析端齿的刚度、阻尼特性影响因素,但模型较为粗糙,很难直接应用于工程实践中。对于螺栓连接结构的研究,Yu L等[12]提出了螺栓法兰连接结构的双线性模型,即拉压刚度不同,且压缩刚度明显高于拉伸刚度;Qin Z[13]发展了一种螺栓连接结构的双线性弯曲刚度分析模型,并将该模型应用于带螺栓连接结构的转子动力特性分析中,结果表当螺栓出现松动现象时,其非线性刚度影响明显增大。Nagaraj B D等研究了盘鼓混合式转子螺栓连接结构在不同转速下的弯曲刚度特性及松动特性,研究表明由于接触面的损失,导致螺栓连接结构连接刚度明显下降,连接结构出现松动[14]。尹泽勇院士提出端齿梁元模型[15],该模型将拉杆转子的圆弧端齿等效为梁单元,梁单元的刚度参数采用有限元方法或试验方法得到。
综上,现有对于圆弧连接结构的研究主要是采用三维有限元方法对结构参数进行分析、优化。对于端齿刚度方面的研究,主要是针对拉杆转子的单排圆弧端齿进行分析,鲜有双排圆弧端齿连接结构刚度特性及其对转子动力特性影响的研究工作。因此本文借鉴已有研究,采用有限元方法获取双排圆弧端齿连接结构的弯曲刚度特性,并将弯曲刚度的非线性特征引入转子系统的动力学模型中,研究了双排圆弧端齿局部刚度非线性对转子动力特性的影响,为双排圆弧端齿的结构设计提供分析方法和数据参考。
1 圆弧端齿连接结构特征
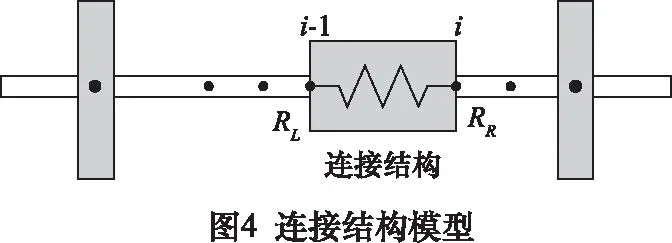
圆弧端齿连接结构用于航空燃气轮机中,主要用于传递高压涡轮和高压压气机之间的扭矩和轴向力载荷,并将高压转子分为两个装配模块,如图1a所示。在转子装配过程中,利用工装将转子内、外侧端齿相互贴紧,然后利用螺栓预紧力进行转子轴向压紧,扭矩载荷通过内外侧齿面传递。端齿的主要载荷包括:螺栓预紧力、转子转速、转子扭矩、转子弯矩和热载荷等,其中预紧力、转速和热载荷为轴对称载荷,所有端齿面载荷相同,扭矩和弯矩为非对称载荷,会导致端齿载荷承载面和非承载面接触状态差异较大。
将端齿结构沿周向展开得到齿形截面如图1b所示,图中θ为压力角,ha为齿顶高,hb为齿根高,hf为齿全高,c为齿顶间隙,hc为齿顶倒角高,hg为山形底高度,λg为山形底角度,Rd为齿根圆角。

2 双排圆弧端齿连接结构弯曲刚度特性
2.1 双排圆弧端齿连接结构有限元模型
有限元模型在ANSYS WORKBENCH18平台建立,由于模型的周期对称特性,采用1/24模型(模型共有48对端齿,24个压紧螺栓)进行分析,并施加周期对称边界条件。材料选取为1Cr18Ni9Ti。模型采用20节点的186单元,全六面体网格,共有单元75 321个,节点295 615个;在端齿的8个配合面处建立TARG170/CONT174接触单元,接触摩擦系数为0.15;螺栓预紧力采用PRET179单元施加。对于法兰盘及轴段部分采用1.0 mm的单元尺寸,并且仅进行单方向结构化,而对圆弧端齿局部及齿根部分进行局部加密,并采用全结构化网格,端齿模型如图2a和2b所示。
载荷边界条件如图2c所示,其中在B界面处施加轴向和周向位移为0约束,载荷包括:(1)螺栓轴向力,40 kN,如图中A处载荷。(2)转速,13 000 r/min。(3)扭矩,20 000 N·m,等效扇区切向力为6 830.6 N,如图2中C处载荷。由于端齿的接触面较多,为了提高计算的收敛性,分3个载荷步依次施加预紧力、转速和扭矩载荷。

2.2 圆弧端齿弯曲刚度特性
分析计算弯曲刚度时,在2.1节基础载荷上,对模型施加弯矩载荷,利用有限元分析得到弯矩载荷作用下的连接结构倾角,从而得到连接结构的角刚度与弯矩载荷的关系曲线如图3所示,可以看出端齿弯曲刚度表现为软特性,弯曲刚度随弯矩载荷的增大而减小。100 N·m低载荷下,圆弧端齿连接结构角刚度有1×108N·m/rad,刚度较好。

首先对切线弯曲刚度与弯矩载荷的关系曲线进行拟合,采用二次指数形式(注:二次指数函数形式为f(x) =axb+c)进行拟合可以得到拟合后的刚度曲线方程为
K=3.603×1013M-2.941+7.896×107
(1)
采用数值积分方法可以得到刚度与角变形量的关系曲线如所示。K与转角θ的关系可以很方便地拟合得到
K=0.000 182 5θ-1.875+7.827×107
(2)
3 圆弧端齿对转子动力特性的影响
3.1 转子系统动力学模型
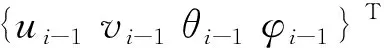
M=KM(φ)·Δφ
(3)
式中:KM(φ)为连接结构的弯曲刚度,该非线性刚度与连接结构在该处的相对转角有关。
记连接结构左右两侧的作用力分别为RL和RR,当转子在连接结构两侧发生相对变形时,连接结构的作用力可以表示为
(4)
式中:Miθ=MΔθi/Δφ,Miφ=MΔφi/Δφ,分别为连接结构在θ和φ方向的反作用力矩。忽略连接结构的质量特征,则在连接结构两侧的反作用力矩相等,即
RL+RR=0
(5)
由力平衡方程可得

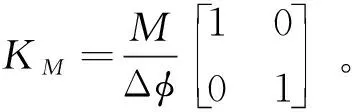
带有连接结构的多盘两支点转子系统如图5所示,系统共有m个节点,仅考虑转子系统的横向振动(忽略轴向振动和扭转振动),系统共有4m个自由度,在系统有限元建模时以连接结构为断点,将系统分为3部分,此时系统动力学方程为
式中的相互作用力RL和RR通过连接结构进行传递。上述分立的方程可用于求解各部分的动力学矩阵,对方程两侧进行求和可以得到系统的总体动力学方程。
3.2 计算模型
高推重比涡扇发动机高压转子系统通常前两阶模态振型为刚体振型,第三阶振型为转子弯曲振型。因此建立的模型要能够反映转子前三阶模态特征。为了模型简化考虑,本章采用如图5所示的两支点三盘转子模型,图中SP为转子支承结构,忽略连接结构的轴向尺寸认为L4的右侧与L5的左侧端点轴向重合。

航空发动机采用端齿连接的高压转子通常采用1-0-1支承方案,前支点位于高压压气机各级盘之间,因此disk1模拟前伸压气机盘,disk2模拟其他压气机盘,disk3模拟涡轮盘,disk2与disk3之间为端齿连接结构。各轴段的参数如表1所示,所有轴段均假设为实心轴,各轴段材料相同,密度为8 240 kg/m3,弹性模量为160 GPa,泊松比为0.31,各轮盘质量和转动惯量参数如表2所示。

表1 轴段参数 mm
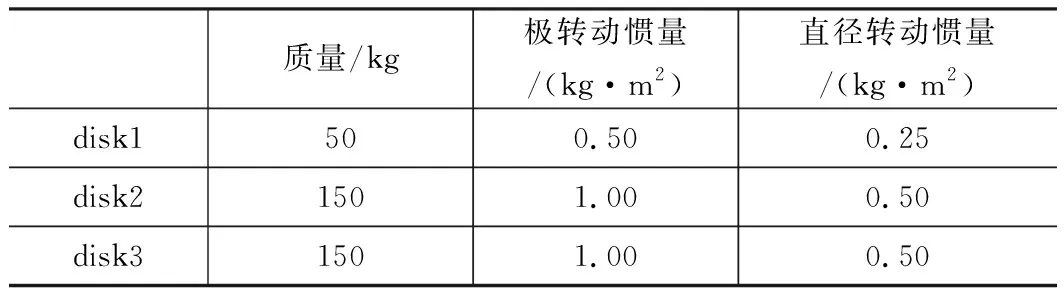
表2 轮盘质量和转动惯量参数
在模型中,转子系统的两处轴承支承的动力学参数为
kxx,SP1=kyy,SP1=2×107N/m,kxy,SP1=kyx,SP1=0,CSP1=0kxx,SP2=kyy,SP2=1×107N/m,kxy,SP2=kyx,SP2=0,CSP2=0
(8)
即忽略轴承支承处的交叉刚度项和阻尼项,且转子支承刚度各向同性。
首先为了验证转子离散模型的计算准确性,在零转速下分析不考虑连接结构时转子各阶固有频率随与节点数量的关系如图6所示,计算误差的参照为节点数为53时计算得到的前三阶频率。由误差图可以看出,前三阶频率误差随节点数量的增加而减小,当n=12时,计算误差小于0.1%,因此在下文计算中均采用节点数为12的模型。

考虑转子连接结构处为刚性连接时,利用上述参数可以得出系统的前三阶振型如图7所示,前两阶振型为刚体振型、固有频率分别为31.9 Hz、56.4 Hz,第三阶振型为一阶弯曲振型,固有频率为78.0 Hz,因此该转子模型能够反映典型航空发动机高压转子系统前三阶模态振型。

转子系统的计算模型按前述方法给出,系统的阻尼系数选定为ξ=0.1,用前两阶无阻尼系统的临界转速折合系统的结构阻尼比,分析可得前两阶系统的临界转速分别为33.14 Hz和57.54 Hz,折合方法为
(9)
式中:α,β为比例阻尼系数;ω1,ω2为前两阶临界转速。
考虑系统的不平衡量为10 g·mm,不平衡量施加于disk2,求的3个盘的振动响应如图8所示。图中考虑的转子频率范围为1~120 Hz,包含模型转子的前三阶正进动临界转速,可以看出:
(1)由于转子连接结构的弯曲刚度低于固定连接的刚性连接,因此考虑连接结构的各阶正进动临界转速均低于固定连接转子,但其影响很小,其中影响最大的为第三阶临界转速,降低1%,主要是由于转子刚体振型,轴段部分的弯曲变形较小,连接结构的刚度较大,且变形小,因此更接近刚性连接。
(2)连接结构的刚度非线性对转子系统的振动响应影响很小,振幅影响均小于0.4%,因此航空发动机转子系统的动力学分析中,可以忽略圆弧端齿连接结构刚度非线性特征的影响。

4 结语
分析了双排圆弧端齿的结构特征和载荷特征,通过建立三维有限元扇区模型,首次得到了圆弧端齿的局部刚度非线性特征,并采用数值拟合方法将该非线性特征引入转子动力学模型,得到了双排圆弧端齿局部非线性刚度对转子动力特性的影响。主要研究结论如下:
(1)弯矩增大时,接触面的有效接触减小,因此双排圆弧端齿连接结构弯曲刚度随弯曲载荷的增大而减小,呈现明显的软特性。
(2)双排圆弧端齿连接结构弯曲刚度较高,在100 N·m低载荷下,圆弧端齿连接结构角刚度为1×108N·m/rad。
(3)双排圆弧端齿连接结构的局部刚度非线性对弯曲临界转速影响较大,临界转速降低约1%,对动力响应的影响约为0.4%;对刚体振型的响应较小,对频率和振幅影响均小于0.1%。

