一种避免轮廓相交的STL模型快速切片方法*
吴 建 吴 婷 陈廷豪 潘成钢
(嘉兴学院信息科学与工程学院,浙江 嘉兴 314001)
随着计算机图形学的发展,用于描述三角网格模型的 STL(stereolithography) 文件己成为 CAD/CAM 系统的一类标准接口文件格式。STL文件不仅占用储存空间少,而且可以满足模型信息在不同软件系统之间高效、及时传输的需求[1]。在对STL文件模型进行3D打印或数控加工时,分层切片处理是其中较为关键的一步,它是通过层切平面与3D模型相交,得到各层截面轮廓信息,因此切片处理的效率和准确性直接影响到模型制作的精度和质量[2]。
由于STL模型表面分布着大量无序的三角片,因此进行分层切片时,需要确定三角片之间的邻接关系,才能将切平面与三角片的交点连接成有序的封闭轮廓。目前,应用较为广泛的STL模型切片算法大致分为两大类:(1)基于交点信息的切片方法。这种方法首先计算切平面与每个三角片的交点,然后对这些交点进行排序以构建成首尾封闭的有序轮廓[3-4]。田仁强等[5]利用二分查找法进行三角片的快速分组,然后求出三角片与切平面的相交线段后,根据各相交线段端点间的冗余信息利用深度优先搜索算法对相交线段优化以创建有序封闭轮廓。Minetto R等[6]将三角片与切平面交点之间的邻接关系创建成哈希表,根据哈希表中存贮的邻接索引依次追踪交点以构建成有序轮廓路径,该方法能够避免三角片公共边交点的重复计算,也无需复杂的网格拓扑关系重建,能够有效提高分层切片处理效率。(2)基于三角片拓扑信息的切片方法。这种方法需要建立相邻三角片之间的拓扑关系,利用拓扑信息找到与其相邻的下一个三角片,依次遍历后即可构成有序的相交三角片集合。这种方法的优点是可直接获得首尾连接的有向封闭轮廓, 无需对交点进行重新排序,但缺点在于建立邻接拓扑信息的数据结构较为费时[7]。王素等[8]将三角片间的邻接关系构建成链表,链表的节点为交点、前驱指针、后继指针构成的结构体,利用链表数据结构依次搜索和插入相邻三角片并求出的交点从而形成首尾封闭的轮廓线。Zhang Z等[9]根据每个三角片的法矢方向确定切平面与三角片交线段的走向,从而确定相交三角片公共边的索引链表,然后按照链表顺序依次进行求交得到有序轮廓路径。徐明月等[10]采用Map容器建立相交边的唯一索引和邻接关系,并按规定的正方向存储交点从而形成最终切片轮廓。徐敬华等[11]利用半边数据结构[12]重构各层相交面片的邻接拓扑关系,并通过哈希表获得有序的网格面片环,最后按顺序求出面片环中各个三角片与切平面的交点获得有序轮廓。
上述两类切片处理方法都是将交点或三角片依次排序成一条有向封闭环来获得最终轮廓的,但是当某一层切片存在开环轮廓或多条轮廓相交等情况时,算法有可能产生错误的结果。对于流行网格模型来说,产生这种问题的主要原因是:模型表面的一些点、边、面与切平面重合,从而导致求交后出现孤立点、悬边和相交边等奇异问题。目前,常用的解决方法是采用Kim h J等人[13]的顶点转移法,该方法首先判断每个三角片的点、边、面与切平面是否重合,若重合则进一步确定这些点、边、面是局部最大还是局部最小,然后将它们沿层切方向向上或向下平移微小距离来解决奇异问题,但是这种改变模型顶点位置的方法有可能因为计算精度误差产生错误。因此,改善分层切片算法的有效性和准确性,对于提高快速成型系统的可靠性和制作精度具有重要意义。
针对上述问题,本文提出一种避免轮廓相交的STL模型切片处理方法,该方法将切平面与模型产生的交点映射成图,利用图论和Delaunay三角剖分相结合的方法来构建有序轮廓,以解决切片轮廓相交等问题。
1 本文方法
本文提出的切片处理方法主要包括以下几个部分:(1)建立与各层切平面相交的三角片集合。(2)计算相交三角片集合中每个三角片与切平面的交点,然后将交点当作节点,交点之间的连接关系当作边,将它们映射为无向加权图。(3)根据图中的节点连通特性,对节点排序以形成有序轮廓,并结合Delaunay三角剖分方法对相交轮廓进行修复。
1.1 建立相交三角片集合
STL模型表面上具有大量散乱的三角片,为了快速计算出各层切平面与模型的交线,避免不必要的计算,应分析出哪些三角片会与切平面相交,建立与切平面相交的有效三角片集合。
假设STL模型沿z轴方向进行分层制造,共分为n层,各层切平面的高度为hi,i=1, 2, …,n。对于每一层切平面, 三角片与切平面的相交位置关系可以分为如图1所示的6种情况。为避免多个三角片产生的交点重复,应排除三角片与切平面只有1个交点(图1d、1e)以及三角片与切平面重合(图1f)的情况,即只有在图1a~1c所示的3种情况下,三角片与切平面有2个交点,从而形成有效交线段。
根据上述分析,在读取模型三角片数据后,计算每个三角片的3个顶点z坐标的最小值zmin、中间值zmid和最大值zmax,并将所有三角片按最小值zmin从低到高进行排序,以加快搜索速度。然后,从第1层切片开始,逐层按照如下条件提取出与切平面hi(i=1, 2, …,n)相交的三角片集合:
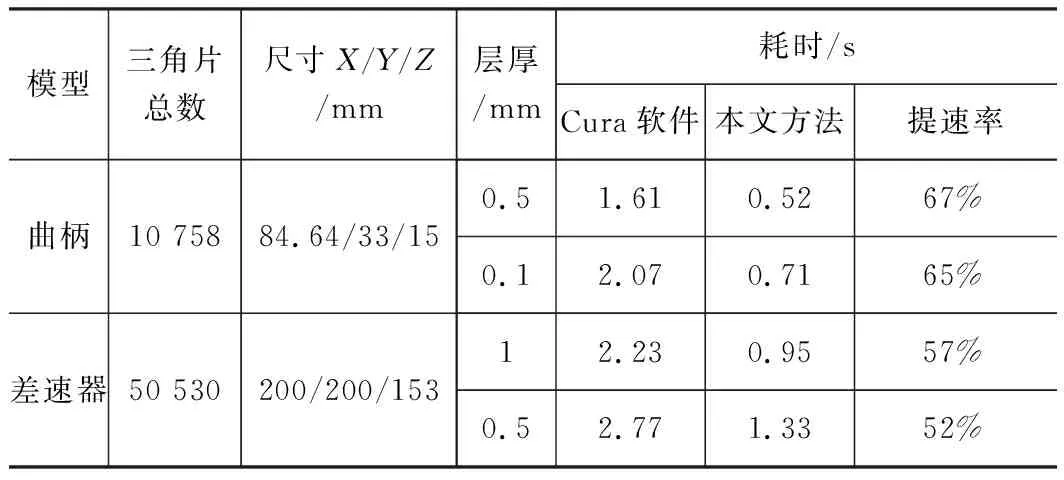
(1)当zmin (2)当zmid=zmin=hi,且zmax>hi,该三角片的下面一条边与切平面hi重合,形成的2个交点分别为该边的2个端点,如图1b所示。 (3)当zmid=zmax=hi,且zmin 在建立的每一层相交三角片集合里,每个三角片与切平面形成2个交点,交点之间形成交线段。如图2所示,切平面与三角片T1形成交线段v1v2,与三角片T2形成v3v4。为将这些线段按照某种顺序连接成首尾封闭的有序轮廓,可以利用基于图论的排序方法。图论是应用数学的一个分支,它是将复杂网络抽象为简单几何图形的一种通用建模方式[14-15],在图像处理、路径规划和工业生产优化等方面有着广泛的应用。其主要思想是将待研究对象中的每个元素映射为图的节点,元素间的连接关系映射为图的边,边的权值代表元素之间的重要性。将研究对象映射为图后,就可以利用基于图论的方法解决节点之间的拓扑排序问题,具体步骤如下: (1) 计算该层相交三角片集合{T1,T2, …,Tm-1,Tm}中每个三角片与切平面的交点,得到集合: (2)对集合V0中的交点进行重复性判断,建立不含重复点的节点集合V={vi|vi≠vj(i≠j)},并将集合V中每个点的索引号映射回集合V0,求得索引向量Id,使V0=V(Id)。 (3)由于V0中每2个连续交点形成交线段,因此建立V中节点之间的边集E为: E= { 其中,wij代表节点vi,vj连成的边 (4)利用节点集合V和边集E,构建图G= (V,E)。 以图2所示情况为例,该切平面与模型共有3个三角片相交,通过求交后可得到交点集合V0= {v1,v2,v3,v4,v5,v6}(图2a)。经过重复性判断,可知v2=v3,v4=v6,v5=v1,去除重复点后得到节点集合V= {v1,v2,v4},将集合V中的这3个节点映射回集合V0,可得索引向量Id=[1, 2, 2, 3, 1, 3],使V0=V(Id);根据V0中每2个连续交点形成交线段的关系,得到边集E= { 将三角片与切平面形成的交点映射成图后,为将这些交点连接成有序的轮廓线,需要对它们进行排序。由于每层切片有时会出现多条轮廓,多条轮廓之间又有可能出现轮廓相交等奇异问题。因此,本文首先利用基于图论的深度优先算法对交点进行排序,然后结合三角剖分方法对相交轮廓进行修复。 对于任意一层切片构建的交点无向图G,建立切片轮廓线的基本过程为:首先将图G进行连通分解,得到图G的连通分量Gi,i=1, 2, …,n;n为连通分量总数。对每个连通分量中的节点利用深度优先算法进行排序,即从图Gi中的某一节点v1出发,搜索与它相邻且未被遍历过的节点v2,然后从节点v2出发,搜索与v2相邻且未被遍历过的节点v3,当循环搜索后回到起点v1,即创建一条有序封闭轮廓v1→v2→v3→v4→v5→v1,如图3所示。 在深度优先的排序过程中,每个节点所邻接的节点个数可能分为以下3种情况: (1)当连通子图内每个节点所邻接的节点个数都为2时,轮廓为简单封闭环,如图3所示。 (2)当连通子图内某个节点所邻接的节点个数为1时,轮廓为简单开环,此时需要以该节点作为起始点重新利用深度优先算法排序。 (3)当连通子图内某个节点所邻接的节点个数大于2时,该连通子图内的多条轮廓相交。例如图4a所示的连通图中,节点8和9所邻接的节点个数大于2,其余节点所邻接的节点个数都等于2。由于3D打印只会在轮廓封闭区域的内部进行材料填充,因此,对于此种类型的节点拓扑排序,只需找到该连通图的外边界节点,而对于内部的多余轮廓分支可予以剔除。因此本文结合三角剖分方法创建有序封闭轮廓,具体步骤为: Step1,将连通子图内Gi的所有节点利用基于约束的Delaunay三角剖分方法[16-17]构建一个三角网格DT。 Step2,构建三角网格DT的边界集合Boundary。边界集合中的边按照如下规则定义:Boundary= { Step3,判断边界集合Boundary中的每一条边界边 Step4,依次连接三角网格DT的边界节点即为连通子图Gi内的有序封闭轮廓。 例如,图4a所示的连通图Gi=(Vi,Ei),其节点集合Vi={1,2,…,9}, 边集Ei= {<1, 2>, <2, 3>, <3, 4>, <4, 5>, <5, 9>, <9, 8>, <9, 6>,<6, 8>,<8, 7>,<7, 1>}。首先将节点集合Vi进行三角剖分得到三角网格DT,如图4b所示,然后构建网格DT的边界集合Boundary= {<1, 2>, <2, 3>, <3, 4>, <4, 5>, <5, 7>, <7, 1>},由于集合Boundary中的边界边<5, 7> ∉Ei,因此将与边<5, 7>相连的三角形△578删除,得到新的三角网格DT,如图4c所示,获取新的边界集合Boundary后,发现边界边<5, 8>∉Ei,因此删除与<5, 8>相连的△589,此时新的三角网格DT的边界集合Boundary完全属于图Gi中的边集Ei,如图4d所示,依次连接边界节点,得到有序封闭轮廓为1→2→3→4→5→9→8→7→1。 采用 Matlab 软件平台,在 Windows 10环境下开发本文方法的分层切片程序, 并以不同 STL模型为实例,利用本文方法与传统方法以及商业软件进行局部切片测试对比, 以充分展示本文方法的有效性。实验在2.4 GHz的CPU、8 GB内存的PC机上运行。 测试模型选取如图5所示的曲柄和图6所示的差速器STL模型,这两个实例模型为流行网格模型,且模型表面都存在和切平面方向平行的三角片,在这些位置进行切片,能够很好地显示算法是否有处理轮廓相交问题的能力。图5a所示的曲柄STL模型,三角片总数为10 758, 模型沿X、Y、Z方向的总长、总宽和总高分别为 84.64 mm、33 mm、15 mm。在切平面P内,产生了如图5b所示的交点。这些交点若采用传统方法,如文献[5]和[8]等,无论选择哪个点作为起始点,都无法形成一个完整的封闭轮廓,会产生如图5c所示的轮廓路径错乱。本文方法首先将切片P内的交点集合映射为图,并利用Delaunay三角剖分方法构建如图5d 所示的三角网格。然后利用图的边集对剖分网格进行裁剪,得到最终的三角网格如图5e所示,顺序连接网格的边界点得到正确的有序封闭轮廓,其结果如图5f所示。图6a为某汽车差速器STL模型,该模型三角片总数为50 530,模型沿X、Y、Z方向的总长、总宽和总高分别为 200 mm、200 mm、153 mm。在该模型的高度为92 mm(切片1)、24 mm(切片2)、17 mm(切片3)处,产生的交点图6b所示,采用传统算法同样产生如图6c所示的轮廓路径混乱,无法构成有效封闭区域,而利用本文方法能够去除多去分支,获得如图6d所示的封闭轮廓。 从以上两个实例的切片测试结果可以发现,当切平面与流行网格模型表面的某些三角片共面时,容易出现轮廓奇异问题。由于传统切片算法是将交点/三角片依次排序成一条有向封闭环来获得轮廓,因此当多条轮廓相交时,在共同相交处由于无法判断分支走向,会造成排序轮廓出现绕行。本文结合连通图和三角剖分的方法,利用Delaunay三角剖分构建封闭区域,利用无向图的边集对剖分网格进行裁剪,以去除多余轮廓分支,从而避免了排序混乱,也避免了顶点转移法[13]带来的精度损失。 为进一步显示本文方法的运行效率,利用本文方法和著名开源切片软件Cura对上述3种模型进行切片耗时对比,其结果如表1所示。可以看出,本文基于图论的深度优先技术,无需复杂耗时的拓扑关系重建,因此算法运行效率比Cura软件提高了接近50%左右,具有显著的效率优势。 表1 本文方法与Cura软件切片耗时对比 本文针对STL三角网格模型,提出了一种避免轮廓相交的切片处理方法。该方法通过相交三角片集合提取、交点图构建和轮廓线排序等步骤,有效构建出模型的各层切片轮廓。实例测试结果表明,本文方法不仅能够准确获取简单封闭切片轮廓,而且能够处理切片轮廓相交的情况。与现有方法相比,本文方法主要优点在于:(1) 将交点映射成图,利用基于图论的强大搜索技术进行拓扑排序的方法避免了耗时而复杂的网格拓扑关系重建。(2) 对于简单封闭轮廓,采用基于图的深度优先搜算策略,算法时间复杂度仅为O(n),n为节点数目,从而极大提高了交点排序效率。(3)对于复杂轮廓,采用基于图和三角剖分相结合的方法,利用图的边集对剖分网格进行裁剪,能够有效去除多余轮廓分支,从而解决轮廓相交问题。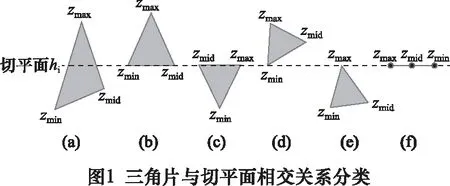
1.2 构建无向图
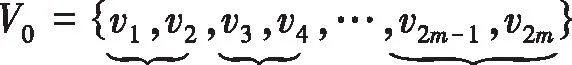

1.3 排序轮廓线


2 实例验证


3 结语

