罗茨泵理论输出流量无脉动的双转子副结构方案*

刘 萍 李玉龙

(宿迁学院机电工程学院，江苏 宿迁 223800)

罗茨转子泵是利用两个相同凸转子旋转过程中所产生的进口真空吸力将流体介质输送到出口的一类容积泵，最早用于罗茨真空泵，应用极其广泛。其中，由两个完全相同转子所形成的非接触式转子副为泵的核心组件，转子叶数常为2～4[1]。在转子啮合过程中，因为啮合点位置的瞬间变化将导致工作腔容积的变化率不是常数，所以转子泵的输出流量不是恒定的而是脉动的[2-3]。输出流量脉动一方面将影响执行元件及其驱动部件的运动平稳性和精度，另一方面也会引起压力脉动，从而使设备系统的管道、控制阀等元件产生振动和噪声[4]，为此，具有恒输出流量即无输出流量脉动一直是转子泵业界的研发重点。

目前常采用多叶数来缓解输出流量脉动，虽然叶数越多脉动越小，却不能真正实现无脉动，又大幅度降低转子的容积利用率[5-6]，往往得不偿失；虽然也开发出像通过直叶顶旋轮廓[7-8]、双啮合弦线轮廓[9-10]或3斜叶60°螺旋轮廓[11-13]来实现恒流量的输出，但是顶旋直叶转子却存在着加工不易、共轭泄漏大及大余隙等问题；双啮合弦线转子间的轴向错位角由额定转速来确定，并不能实现任意转速下的恒流量输出，同时也存在着与顶旋直叶转子同样的问题；3斜叶60°螺旋转子也存在着加工不易、轴向力补偿、容积利用率低及不同端面轮廓构造引起的大余隙等问题。其中，大余隙中的输出介质将随着转子副的旋转又被带回到输入端，从而降低容积利用率[14]及导致比如罗茨真空泵的真空度不达标等现象[15]。鉴于此，拟通过4个相同直摆线转子构成的双转子副，直接实现两单一转子副理论输出流量合并后的定值理论输出流量即无理论脉动。

1 泵无理论脉动的双转子副构造

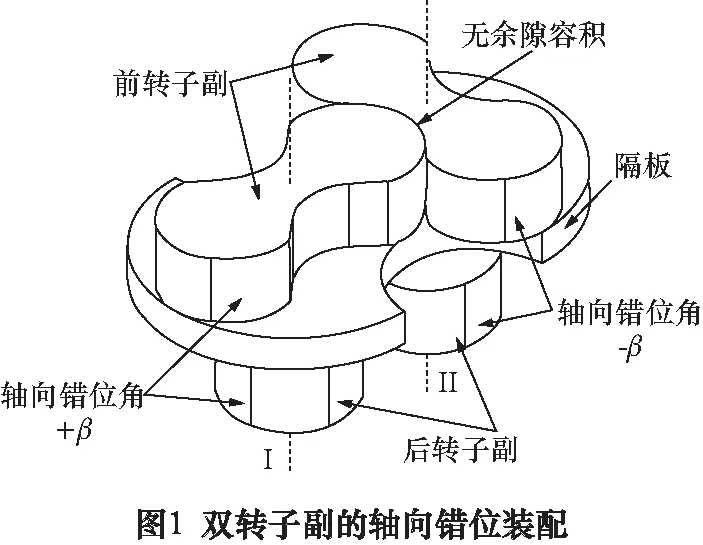
以2直叶为例，双转子副为由4个相同摆线转子所构成的前、后转子副，及完全隔开前、后转子副内各自介质流量的防窜隔板组成，如图1所示。其中，转子轴I上的前、后转子按轴向错位角+β的方式间隔装配，转子轴II上的按-β方式间隔装配。

2 直摆线转子的半叶轮廓构造

以2直叶为例，摆线转子的半叶轮廓由节圆外侧的峰圆弧段01、外摆线段12与节圆内侧的内摆线段23、谷圆弧段34首尾相连组成。如图2所示。

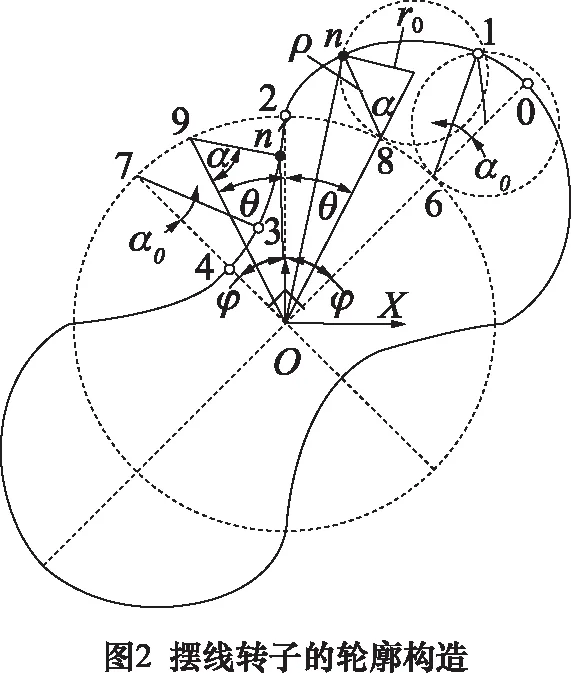
其中，半叶轮廓相应的端点和连接点依序为位于峰对称轴O0上的峰点0、外轭点1、位于中对称轴O2和节圆上的中节点2、内轭点3和位于谷对称轴上O4的谷点4，O0、O4与节圆的交点为峰节点5、谷节点6，O0与O4的交点为转子中心O，O0与O2、与O4间的夹角均为φ=π/(2N)，N为转子叶数。12、23段为滚圆外、内滚切节圆时所对应的部分外、内摆线。

设转子的形状系数设为ε，节圆半径为r，ε等于O0的长度除以节圆半径r；01段为以峰节点6为圆心、(ε-1)r为半径，圆心角为α0的一段顶圆弧，34段为以谷节点7为圆心、(2-ε)r为半径，圆心角为α0的一段谷圆弧。12段上任一点n和与之对应的23段上任一点n′处的法线与节圆的交点为瞬节点8、9，8n、9n′的长度为瞬半径ρ，∠2O8、∠2O9为0°～φ内的瞬转角θ，∠n8O的补角、∠n′9O均为瞬节角α，这样转子轮廓上的n、n′与配对转子上的n′、n将形成互为共轭的几何关系[16]。

设滚圆半径为r0，滚径比i=r0/r。依据滚圆在节圆上外切纯滚动的圆外摆线成形原理，由节圆上26劣弧长等于滚圆上16劣弧长的

r0(π-2α0)=rφ

(1)

得

α0(N,i)=π/2-φ/(2i)

(2)

且由α0≥0，得

i≥1/(2N)

(3)

同理，由节圆上28劣弧长等于动圆上n8劣弧长，得

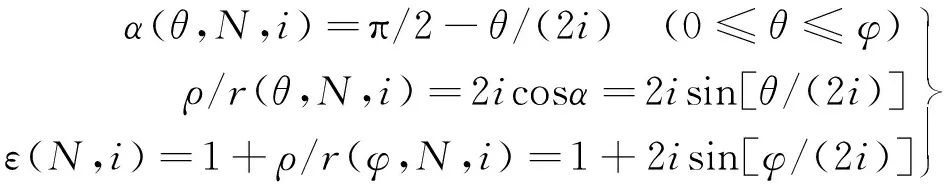
(4)

外摆线段12与内摆线段23在图2中XOY直角坐标系下的参数化坐标方程为

(5)

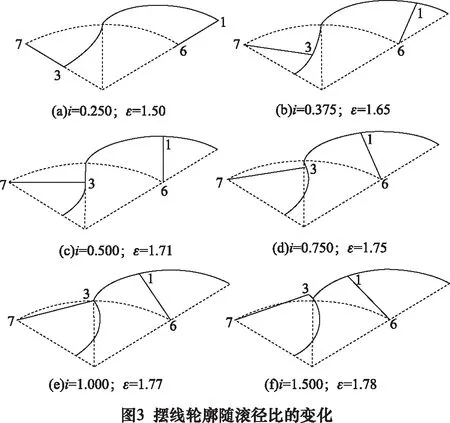
摆线转子的半叶轮廓随滚径比的变化，如图3所示。其中，滚径比i越大，形状系数ε越大，i=0.5时的内摆线段23为位于中对称轴O2上的直线段，i=1时的内摆线段23收缩为中节点2，i>1时的内摆线段23段因几何干涉不符合作为共轭轮廓段的要求。

结合式(3)，则滚径比的取值范围为

1/(2N)≤i≤1

(6)

3 单一转子副的理论输出流量

在单一转子副的排出腔内，图4给出了剖面线所示密闭排出容积的截面随共轭位置点n的变化情况。

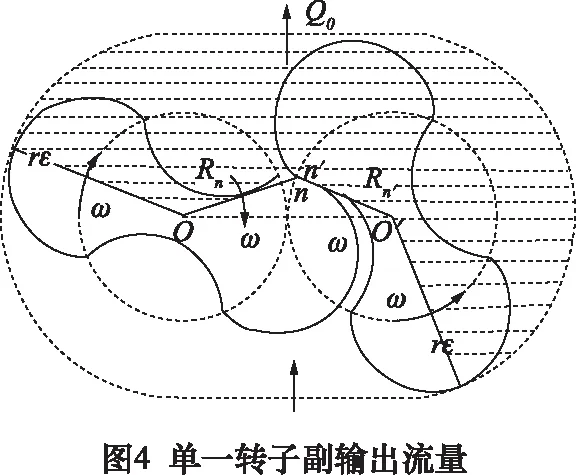
其中，转子、配对转子的中心为O、O′，共轭点n处的共轭半径分别为Rn、Rn′。设b为转子的宽度，ω为转子的旋转角速度，随着转子副连续共轭旋转，由共轭位置点n处半径Rn、Rn′的动态变化，得该密闭排出容积的变化率，即单一转子副的理论输出流量Q0为

(7)

其中

(8)

将式(5)代入(8)，得

(9)

则单一转子副的无量纲理论输出流量q0为

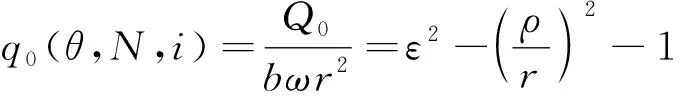
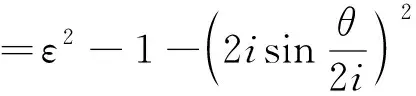
(10)

即其理论输出流量具有正弦函数的平方特性。

由式(10)中的q0及式(4)中的ρ/r知，外轭点1或内轭点3共轭时，q0将取得最小值q0,min；中节点2共轭时，q0将取得最大值q0,max。其中

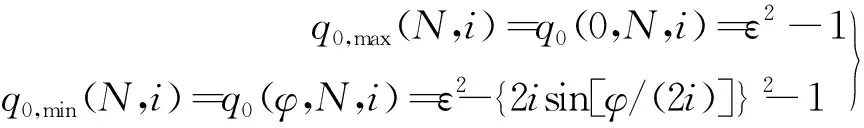
(11)

由式(10)，得单一转子副的平均理论输出流量为

(12)

单一转子副的理论流量脉动系数为

(13)

4 双转子副的理论输出流量

设前、后转子副各自的无量纲理论输出流量为q1、q2，则由

(14)

得双转子副的无量纲理论输出流量q为

(15)

其中:形状系数越大，无量纲理论输出流量q越大。

当要求式(15)的q(θ)为不随θ变化而改变的恒定值时，则必须存在

φ/(2i)=π/2

(16)

此时，前、后转子副各自的理论输出流量分别具有正弦函数、余弦函数的平方特性。

且由φ=π/(2N)和式(2)，得

i=1/(2N);α0=0°

(17)

此时，图2中的01顶圆弧和34谷圆弧不存在，即半叶轮廓仅有外摆线和内摆线构成。

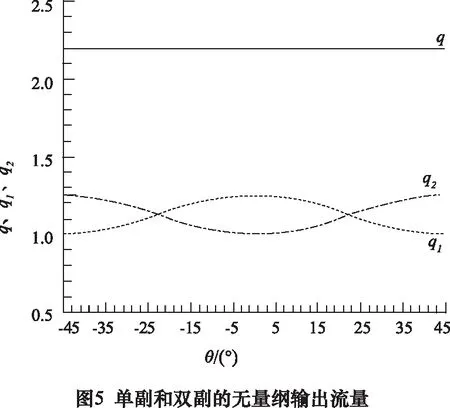
由式(4)中形状系数ε的公式知，叶数N越少，形状系数ε越大，即无量纲理论输出流量q越大，故取N=2。此时i=0.25，转子将取得1.5的最大形状系数ε，无量纲理论输出流量q也将取得2.25的最大值。其中，δ0=0.22，q0,av=1.125，β=φ=45°，单副和双副的无量纲理论输出流量，如图5所示。

5 结语

(1) 摆线轮廓是能通过双转子副的结构方案，来实现定值理论输出流量即无脉动的唯一曲线类型。

(2)在基本维持泵原有结构的前提下，双转子摆线副能克服现有无脉动方案中所存在的问题，且能实现任一转速下理论输出流量的无脉动。

(3)2直叶、0.25滚径比和45°轴向错位角能实现2.25的最大无量纲理论输出流量。

(4) 2直叶摆线转子的轮廓构造简单，易加工、无余隙且容积利用率高。