四元数联合传递率在结构状态检测中的应用

任同群,郑培珍,徐征,王晓东

(1.大连理工大学精密与特种加工教育部重点实验室,辽宁 大连116024;2.大连理工大学 微纳米技术及系统辽宁省重点实验室,辽宁大连116024)

0 引言

在实际工程中,多数情况下结构的激励未知或不易测得,这导致无法准确识别结构的模态参数,进而限制了基于结构参数变化的损伤检测方法的应用。相比之下,直接基于振动响应信号分析的状态检测方法不影响结构正常运行且费用较低,已成为目前结构健康检测的研究热点,也得到了广泛的工程应用,其基本过程包括损伤特征提取与分类[1-4]。

在众多所提取的损伤特征中,振动传递率反映了结构两测点之间的全部力学特性,可表示为结构刚度、阻尼和质量等物理参数的函数。Fauziyah等人[5]利用加速度计阵列测量多泵间的振动传递率,实现了多泵的故障诊断。Dong等人[6]基于振动传递率对随机激励下的螺栓松动监测进行了研究,克服了常用的振动方法在发现螺栓局部松动方面的不足。杨斌[7]采用相空间重构方法进行振动传递率函数分析,重构振动传递率函数矩阵,并以其奇异值熵作为损伤指标,提高了检测方法的抗干扰性。Luo等人[8]以加权传递率作为损伤指标评估结构状态,提高了TF的信噪比。Chen等人[9]利用神经网络,提取基于振动传递率的损伤诊断指标,并验证了其正确性。

在上述研究中,振动传递率仅基于单通道信号计算获得。在工程应用中,测试信号是实际振动在传感器敏感方向的投影。因此,基于单通道信号的方法在处理空间振动问题时容易陷入困难。为解决此问题,通常采用多加速度计或三轴加速度计获取空间振动信号,进行单通道信号处理及特征提取后再进行特征融合。但是,这种处理方法忽略了信号通道之间的关联性,融合后会带来失真甚至是虚假的结果。因此,有必要将多通道信号视为矢量信号,进行同时处理,以保证通道间的关联性。四元数三个虚部的运算是等价的,因此非常适合表示三维矢量信号。例如,Rehman和Mandic[10]研究了三维信号的经验模态分解,并证明三通道信息联合处理时会获得更好的精度。Tong[11]采用四元数K-LT对故障异步电机进行特征提取,但处理的数据仅限于时域四元数振动序列。Yi和Lv等人[12-13]描述了四通道信号的相关性,提出一种基于凸优化的四元数奇异谱分析方法。Ren等人[14-15]采用四元数,构建三轴信号的振动传递率,并验证了K-LT法和DQWT法,取得了较好的结果。此外,Ell和Sangwine[16-19]针对四元数傅立叶变换和相关分析问题进行了合作研究,相关研究成果为四元数频域分析奠定了理论基础。

本文提出了一种基于QTJT的状态检测方法,先后采用K-LT和DQWT技术提取状态特征指标向量,然后定义状态特征指标向量之间的欧氏距离并将其作为状态指标,针对轨道结构扣件松脱及内部温度力的变化,进行了状态检测与识别。通过在无砟轨道试验平台上开展实际实验,验证该方法的有效性。

1 四元数联合传递率相关理论

1.1 四元数传递率计算

对于单通道信号,振动传递率定义为结构两测试点的时域序列xi(输出)和xj(输入)的频谱比值。它描述了振动(振幅和相位)如何在结构的两个测试点之间进行传递。假设一个n自由度线性结构受外力f(t)=[f1(t),f2(t),…,fn(t)]的激励,如果f(t)具有形如白噪声的均匀谱密度,则fk(t),k=1,2,…,n的傅立叶变换则为一个常数D。此时,由节点j到i的振动传递率计算公式为

式中:Ai(w),Aj(w)分别为节点i,j处振动加速度信号的频谱;H(ω)为n×n的频响函数矩阵,H(ω)=-(ω2M+iωC+K)-1;M为n×n的质量矩阵;C为n×n的阻尼矩阵;K为n×n的刚度矩阵。如果激振力只作用于一点k,式(1)变为

上述两情形中,激振力仅提供了振动能量,并未参与传递率的计算。此时,振动传递率仅与激励位置有关。根据式(1)和式(2),振动传递率与频响函数有关,反映了结构的内在特性。因此,振动传递率可以用于结构状态检测。

采用三轴加速度计采集获得结构三个正交方向的振动信号ax(t),ay(t),az(t),可以构建纯虚四元数的时域序列aq(t)=[aq1,aq2,…,aqM],其中,aqr=iaxr+jayr+kazr,r∈[1,2,…,M],M为序列维度。此时,传统的基于单通道信号频谱之比的振动传递率不再适用。此时四元数传递率可定义为

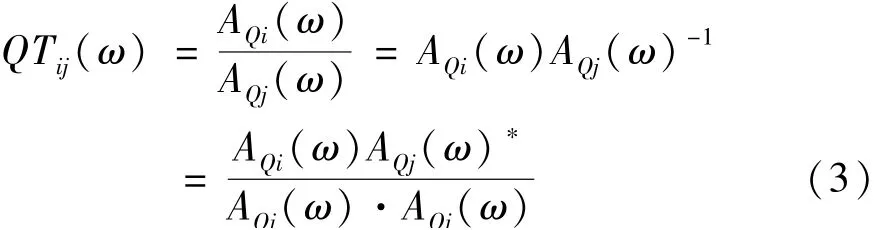
式中:AQ(ω)为四元数谱;·为四元数点乘符号;∗为共轭运算符号。

Ell提出了四元数傅立叶变换用于分析二维线性定常系统[16-17],其原始定义可表示为

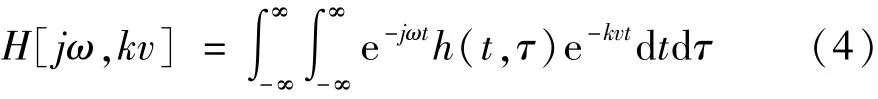
式(4)定义了二维函数h(t,τ)从空间域(t,τ)向空间频域(jω,kv)的转换。四元数傅立叶变换最早用于彩色图像的分析,具体形式[18]如下

式中:μ为随机单位纯虚四元数;f(m,n)为M×N彩色图像矩阵(三颜色通道构建纯虚四元数);(m,n)和(u,v)分别为空间域和空间频域的坐标。对于纯虚四元数振动时域序列aq(t),可视其为1×N的彩色图像,因此,aq(t)的四元数谱计算公式为

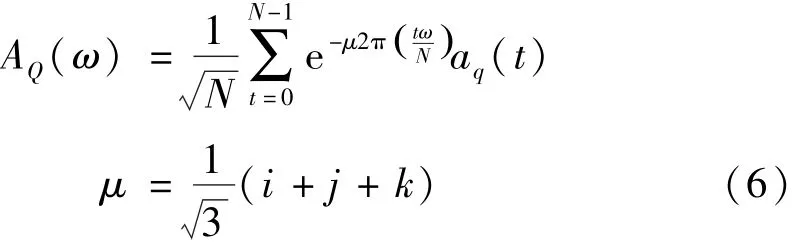
由式(6)可知,AQ(ω)也是四元数序列,故由频谱之比定义的四元数传递率也是在频域内的四元数序列,和普通传递率一样,也包含了全部的结构内在特性。

1.2 四元数传递率特性

参考实数信号的傅立叶变换,四元数时域序列亦可以由不同频率分量的四元数信号的线性组合来表示。类似地,在四元数傅立叶变换中,可将变换后的模值作为纵坐标得到四元数幅频谱。

不失一般性,构造如下三通道信号[x(t),y(t),z(t)],三个通道分别由不同频率的正(余)弦信号组成

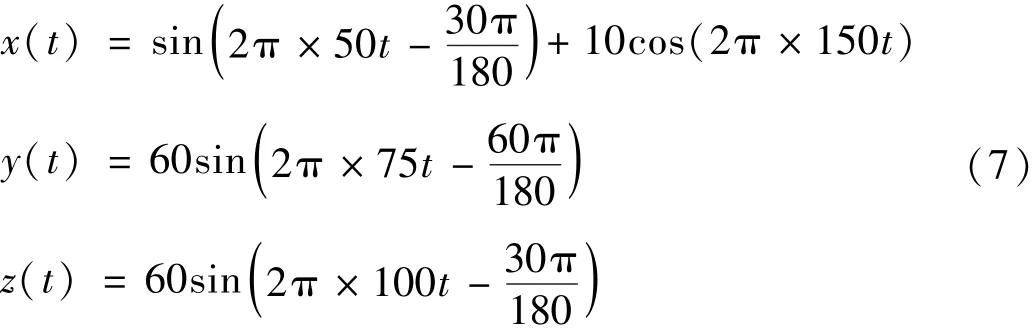
对x(t),y(t),z(t)三个单通道信号分别进行独立的傅立叶变换,得到幅值谱如图1(a)所示,然后将三个通道信号联合成[x(t),y(t),z(t)],构建四元数序列并进行四元数傅立叶变换,可得到整体的频域信息,其幅值谱如图1(b)所示。对比可以发现,联合信号的四元数频谱包含了全部信号的频率成分,是三通道信息的无损融合[20]。

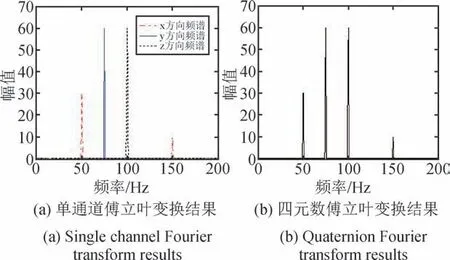
图1 四元数傅立叶变换Fig.1 Quaternion Fourier transform of three-channel joint signal

当振动方向偏离传感器的敏感方向且仅使用单轴传感器时,振动幅值会减小,但频率不变。如果传感器的安装方向不能严格一致,传统的基于单通道信号的振动传递率将偏离理论值。在实际工程应用中,很难保证检测时传感器的安装方向严格一致。不仅如此,若振动方向是时变的,将直接导致传递率的时变,进而造成结构状态的误诊断。

图2 (a)描述了任意向量v∈R3绕3D单位向量u旋转2θ的情形。用上节中的定义将向量u和v扩展为纯虚四元数,则旋转之后得到的向量v′计算公式为

式中:euθ为单位四元数的指数形式,euθ=cosθ+usinθ。式(8)等价于三轴加速度计的测量坐标系原点不变,坐标系的方向绕向量u旋转2θ,如图2(b)所示。

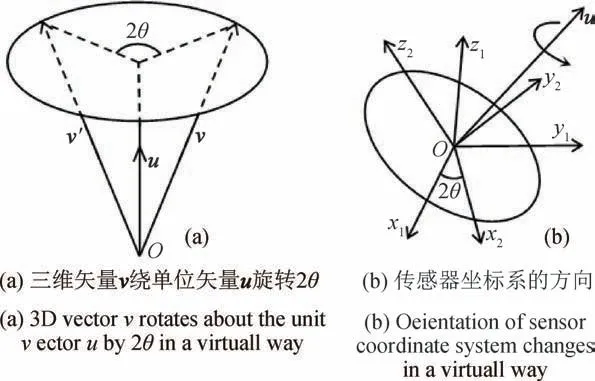
图2 四元数描述空间向量旋转Fig.2 Quaternion describes vector rotation in space

向量v′的模值计算公式为

上述分析表明当采用三轴加速度计时,只要安装位置固定,无论其安装姿态如何变化,均可如实采集获得空间振动信号。进而可推论,两测点的三轴加速度计位置固定且不考虑噪声干扰时,不论安装姿态如何,式(3)的四元数传递率幅值均为其理论值。为证明上述推论,基于无砟轨道综合试验平台,获得两测点振动信号的四元数时域序列,通过理论计算将测点A,B的信号分别绕u1,u2旋转π/6和π/3,获得三组四元数振动传递率,即初原始、仅旋转A信号以及旋转A/B信号的四元数振动传递率,如图3所示。由图3可知,当传感器姿态发生变化时,四元数传递率的实部与虚部幅值均发生变化,但整体幅值不变。其中,u1,u2分别为

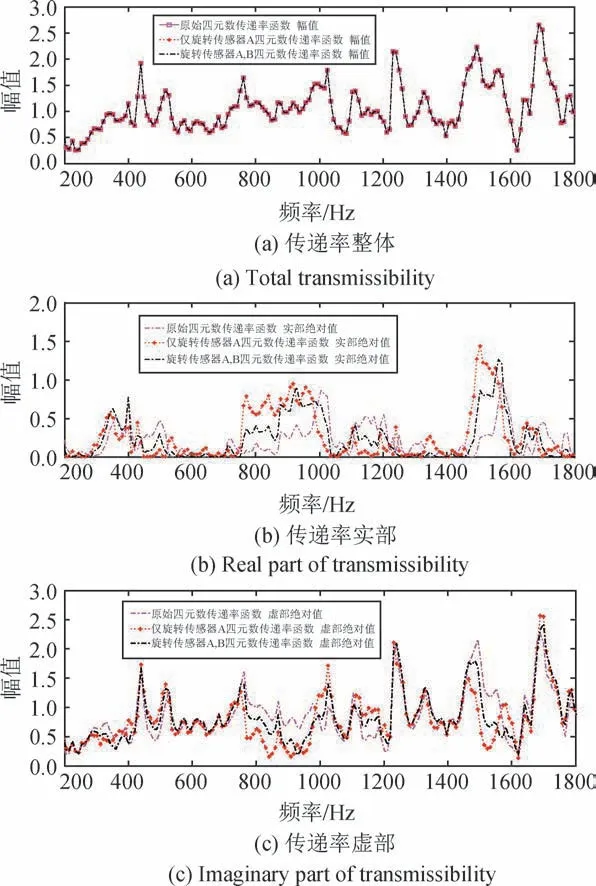
图3 信号旋转前后的四元数传递率幅值Fig.3 Amplitude of quaternion transmissibility before and after signal rotation

1.3 对偶树四元数小波变换

对偶树小波变换由离散小波变换(discrete wavelet transform,DWT)和复小波变换(complex wavelet transform,CWT)拓展而来,基于二维解析信号和希尔伯特变换(Hilbert transform,HT)构造而成。与实小波变换相比,对偶树四元数小波变换可以获得多角度、多尺度下的一个幅值和三个相位信息,同时具有良好的时移不变性[21]。

为了推广到二维,Bülow[22]根据四元数傅里叶变换给出了四元数解析信号的定义,给定一个实数二维信号f(x,y),其四元数解析信号定义为

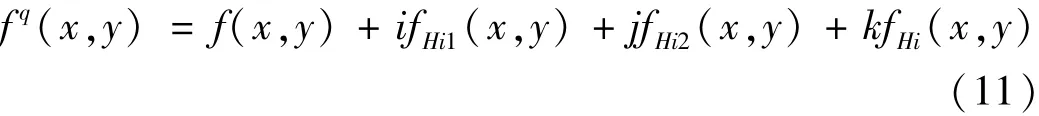
式中:fHi1(x,y)和fHi2(x,y)分别为沿x和y轴的希尔伯特变换;fHi(x,y)为完整的希尔伯特变换。

二维离散小波变换由一维离散小波变换沿两个正交基的张量积构成,可表示为尺度函数φ(x)φ(y)、水平方向子带函数φ(x)ψ(y)、竖直方向子带函数ψ(x)φ(y)和对角线方向子带函数ψ(x)ψ(y)的组合[23]。相似地,四元数小波同样具有一个尺度函数和三个小波子带函数,即将二维离散小波变换与三个实小波(由一维希尔伯特变换得到)组合构成一个四元数,从而得到二维解析小波。以对角子带ψ(x)ψ(y)为例,其二维希尔伯特变换计算公式为

式中:(ψh,ψg)为特定滤波器h和g对应的小波函数,它遵循{ψh,ψg=HT(ψh)}的原则。式(12)中的每个分量均可由一维对偶树复小波的组合计算。因此,对角线子带四元数小波计算公式为

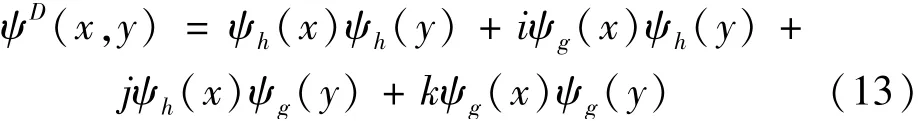
同理可得水平、垂直子带四元数小波以及四元数尺度函数[24]分别为

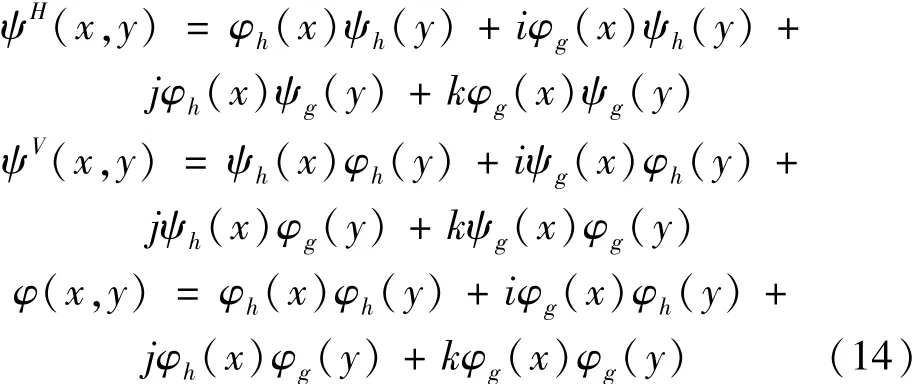
对偶树小波变换的计算细节可参考文献[25]。

2 基于四元数联合传递率的状态检测方法

2.1 卡洛变换(K-LT)法

K-LT是一种基于对象统计特征的最优正交变换。它可以消除统计相关性,但保留分类信息。将状态已知条件下测量得到的四元数传递率模值向量作为训练样本,并构建为状态矩阵SQ=[s1,s2,…,sN]∈RM×N,其中M为测量四元数传递率的长度,即参与运算的有效谱线数目,N为测量的传递率数目。状态矩阵SQ的协方差矩阵CQ∈RM×N可以分解为

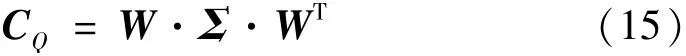
式中:W=[w1,w2,…,wN]∈RM×N为特征向量矩阵张成的特征子空间;Σ=diag(λ1,λ2,…,λN)∈RN×N为特征值矩阵,且λ1≥λ2≥…≥λN。对任意训练四元数传递率模值向量sj,j=1,2,…,N,将其投影到特征子空间可获得新的向量sj′=WT·sj。此时,s′j可作为状态索引向量。将未知状态下测得的四元数传递率模值向量以同样方式投影到特征子空间,获得投影向量s′t,然后计算s′j和s′t的欧氏距离,称取得最小欧式距离的投影向量为匹配向量,即同一状态。

2.2 对偶树四元数小波变换(DQWT)法

如图4所示,将同一状态下4个测试四元数传递率模值向量叠加,构建状态特征图。图4表明同一状态下的不同样本有很大的相似性而又有着局部的差异性。

图4 四元数传递率灰度图Fig.4 Grey-scale map of quaternion transmissibility

对状态特征图进行对偶树小波变换,其系数可构成一个矩阵F,即

F的第一列包含图像的低频信息,第2~4列分别代表图像在水平方向、垂直方向和对角线方向的高频信息。

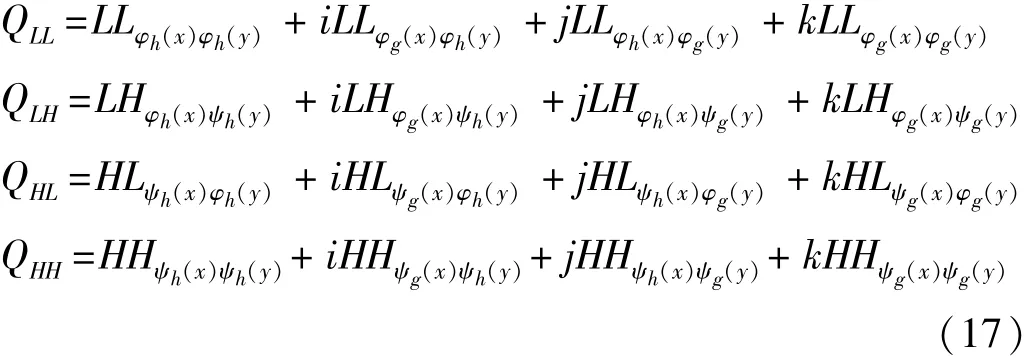
对偶树小波变换的系数包含了一个幅值信息和三个相位信息。F的每一列可以构成式(17)的四元数,计算其每个四元数的幅值和相位,并重新组合得到幅值-相位矩阵

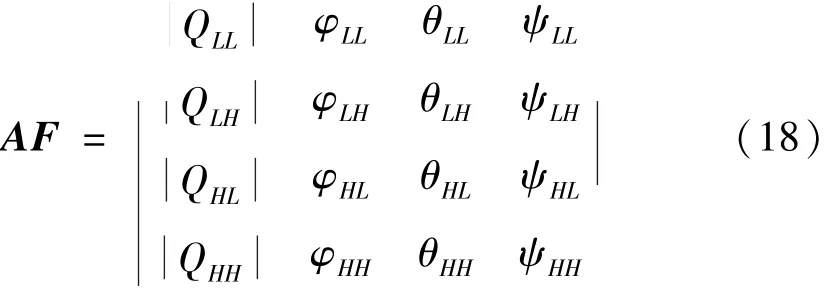
获得每种已知状态下的多组四元数传递率,构建状态特征图作为训练样本,对其进行对偶树四元数小波变换得到低频幅值相位向量AFi,同样地,构建未知状态下的状态特征图,计算其低频幅值相位向量AFj,计算AFi和AFj之间的最小欧式距离并将其作为状态识别指标,与上节方法类似。取低频幅值相位信息,既综合考虑了二维传递率图像的幅值相位信息,又减小了单传递率的测量不确定性对检测结果的影响,且降低了原始数据的大小。

3 状态检测实验

实验对象为总长20 m的CRTS-I型“无砟轨道综合试验平台”,钢轨两端锁紧,中间由配套的WJ-7型扣件锁紧。实验时在轨底隔跨两组扣件安装两个三轴加速度传感器PCB 356A33,采用力锤YD-5T在实验区域左侧某处的轨顶施加激励,敲击方向垂直于轨顶并保持激励位置固定,以10 kHz的采样频率采集振动信号,采集设备为DHDAS-5902动态信号采集分析系统。实验现场及传感器布置如图5所示。

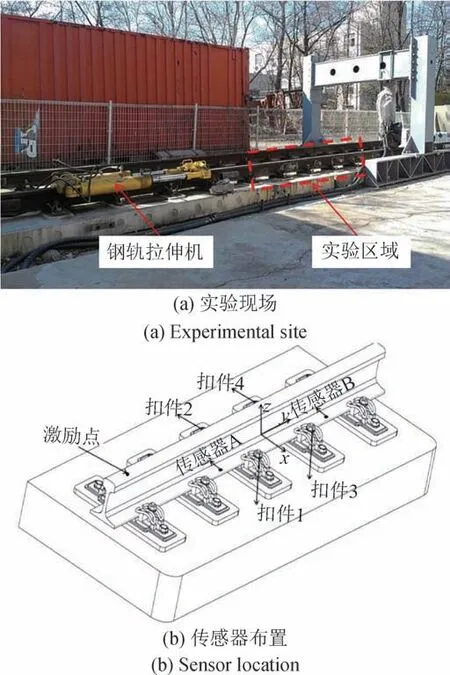
图5 实验现场及传感器布置Fig.5 Experiment site and sensor location

首先,利用钢轨扣件的松脱与否模拟不同状态,根据扣件松脱顺序设置五种不同工况,分别为:扣件全部锁紧,扣件1松脱,扣件1和2松脱,扣件1,2和3松脱以及4个扣件全部松脱。每种工况下,在左侧激励点用力锤激励40次。根据前述四元数传递率函数的计算方法,计算得到每种工况下的40组传递率函数。图6为工况1下的全部40次四元数传递率,取200~1700 Hz部分传递率函数,可见其重合性很好[26]。一方面,说明了传递率计算的正确性;另一方面,也验证了四元数传递率函数仅由激励位置和结构自身特性确定,而与激励大小无关的结论。

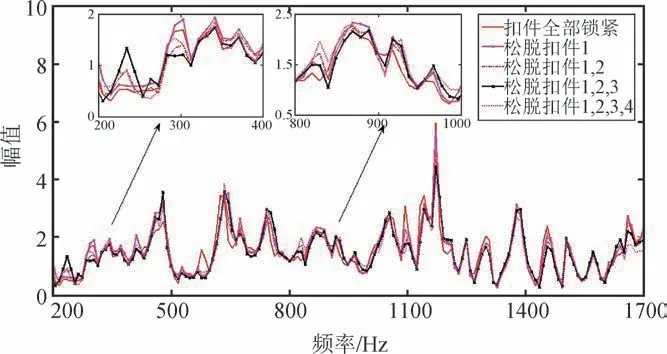
图6 工况1下40组原始四元数传递率函数幅值谱[26]Fig.6 Amplitude spectrums of 40 sets of original quaternion transmissibility under situation 1[26]

分别求取五种工况下的40组四元数传递率函数平均值,如图7所示。在选取频段内,传递率谱线大体重合,仅在部分频率区间存在较明显差别。这是因为相较实验区域,试验平台在较长一段钢轨上的扣件是锁紧的,仅松脱局部相邻扣件对整体结构的影响较小。

图7 五种工况下平均四元数传递率函数幅值谱Fig.7 Average amplitude spectrum of quaternion transmissibility under five situations

采用2.1中基于K-LT的方法进行状态识别,分别取五种工况的前30组传递率函数作为训练样本,后10组作为测试样本,用来验证该方法的有效性。检测结果如表1所示,其中,测试QTJT(i)下的第一列数字表示与之取得最小欧氏距离的训练样本列序号,正确识别时第j测试组下的QTJT(i)对应序号应为30×(j-1)+1~30j;第二列表示状态识别结果,‘√’表示识别正确,‘×’表示识别错误。由表1可知,该方法取得了98%的状态识别正确率。

表1 基于K-LT方法扣件松脱状态检测结果[26]Tab.1 Detection results based on K-LT method

基于上述数据,采用2.2中DQWT方法进行状态识别处理,分解层次取2,每种状态下计算得到的40组QTJTs模值矩阵V∈R152×40,每4组QTJT作为一个样本,每种状态得到10组样本,其中前6组作为训练样本,后4组作为测试样本。识别结果如表2所示,状态i(i=1,2,3,4,5)正确的匹配范围应为6(i-1)+1~6i。由表2可知,该方法状态识别正确率达到了100%。

表2 基于DQWT方法扣件松脱状态检测结果[26]Tab.2 Detection results based on DQWT method

采用LG-900型液压钢轨拉伸机拉伸钢轨,模拟钢轨内部纵向温度力的变化,分别设置拉应力:0,10,20,30,40,50 MPa。首先,松脱全部扣件以释放钢轨内部纵向温度力,稳定后拉伸机分别以上述设置应力动作进行钢轨拉伸,而后再将全部扣件锁紧,缩紧力矩为150 N·m。同样地,每次拉伸之后按照前面的实验方法,依次松脱相邻两组扣件,得到30组状态,每种状态采集20组振动信号,计算得到20组四元数传递率。在每种状态下,以其前12组QTJT分别构建3个状态特征图作为训练样本,以后8组QTJT分别构建2个状态特征图作为测试样本,表3为该实验的状态组织安排情况。基于DQWT方法进行状态识别处理,每种状态的匹配范围应为3(i-1)+1~3i,所有样本的识别结果如表4所示,该方法状态识别正确率达到了100%。

表3 温度力、扣件松脱综合实验结构状态安排Tab.3 Structure state arrangement for comprehensive experiment of temperature force and fastener looseness

表4 的实验结论表明,该方法可实现分辨力优于10 MPa的钢轨温度力变化识别。基于铁路轨道相关标准,钢轨的相关参数如下:截面积为7.745×10-3m2,线膨胀系数α=0.0118 mm/(m·℃),弹性模量E=2.1×105 MPa。则轨温有1℃变化时所产生的内部纵向力计算公式为

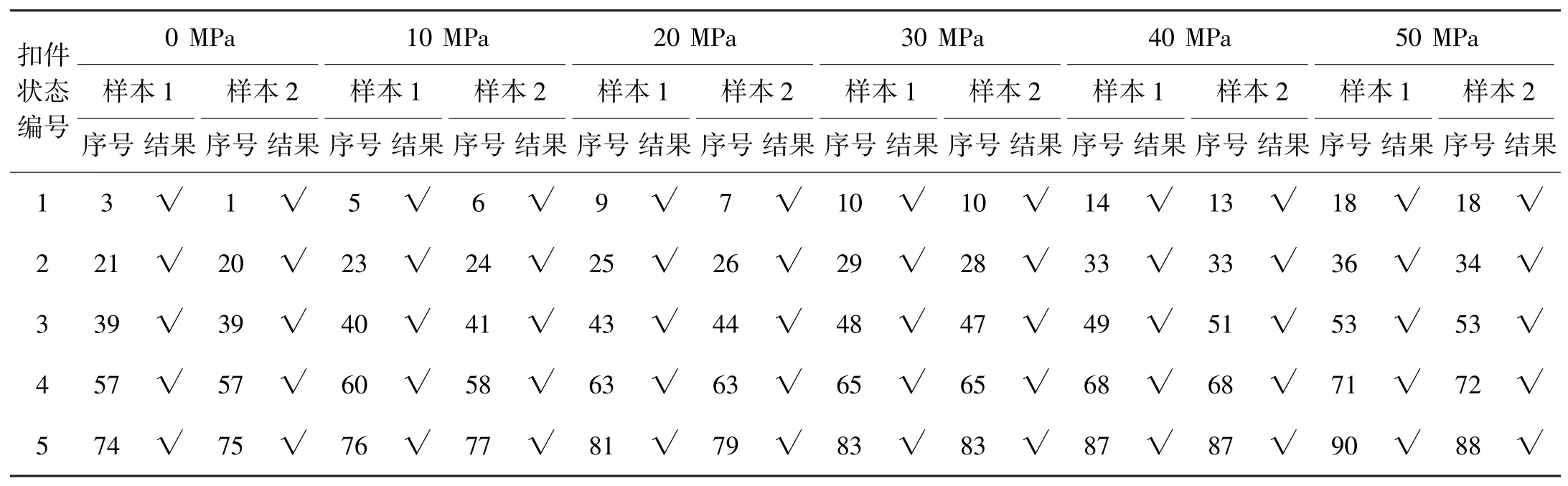
表4 基于DQWT温度力、扣件松脱综合钢轨状态检测结果[26]Tab.4 Detection results based on DQWT method for the comprehensive experiment

LG-900型液压钢轨拉伸机的油缸截面积为S=3.352×10-3m2,则其10 MPa的拉应力对应10 MPa×S=33520 N的拉力。进而,10 MPa的拉应力相对应的钢轨温度变化为33520 N/19192.11 N×1℃=1.75℃。因此,本方法可实现分辨力优于10 MPa的钢轨温度力变化识别,相当于锁定状态下1.75℃的轨温变化。

4 结论

将传统的基于单通道信号的振动传递率推广到多通道信号的四元数振动传递率,并结合K-LT技术和DQWT,给出了基于四元数联合传递率的的结构状态检测方法。通过在无砟轨道试验平台上的实际试验,验证了该方法的有效性,状态识别结果正确率高于95%。上述方法提供了一种识别状态变化是否存在的解决方案,未来可以通过增加测试点和依次识别相邻四元数传递率,进一步发展为同时识别状态变化的存在和位置。更重要的是,该方法保留了振动传递率的理论值,对传感器的安装方向没有严格的要求,在实际应用中具有明显优势。特别是基于DQWT的方法,综合考虑了多个被测传递率,降低了单次测量不确定性的影响。本文的研究为推动直接基于振动响应信号分析的状态检测方法发展起到了积极作用,具有重要技术应用价值。