冻融作用对不同初始状态基坑稳定性的影响研究

赵容舟， 梁二雷， 姚晓亮， 余 帆

（1.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州 730000； 2.中国科学院大学，北京 100049；3.中国建筑第四工程局有限公司西北分公司，陕西西安 710075； 4.西安理工大学，陕西西安 701148）

0 引言

季节冻土区广泛分布于我国北方地区，约占国土面积的53.5%［1-2］。在季节冻土区，随着季节交替变化，地表土体处于反复冻结和融化状态［3］。受冻融循环这种强风化作用的影响，季节冻结层内土体的物理力学性质会发生显著变化［4-7］，进而影响公路、铁路、渠道、基坑和隧道等工程设施的施工建设和安全运营［8-14］。目前，我国处于城市建设的快速发展阶段，由冻融作用引起的基坑工程稳定性问题日益突出，如支护体系崩裂、脆断，坡顶或基坑周围地面出现裂缝，基坑整体失控坍塌等［15-19］。因此，为了更好地控制并避免此类灾害的发生，开展季节冻土区冻融作用对基坑工程稳定性的影响研究尤为重要。

现阶段用以基坑稳定性评价的方法主要基于融土地区基坑稳定性分析理论，包括：极限平衡法和强度折减法［20-26］。极限平衡法视土体为刚体，不考虑土体的应力应变关系，无法反映基坑侧壁土体的变形破坏过程；强度折减法突破了极限平衡法的理论缺陷，能合理描述基坑侧壁土体的应力应变关系，通过逐渐增大强度折减系数的方法来分析基坑的稳定性［27-29］。相较于融土地区，季节冻土区基坑的稳定性还会受到季节冻结层的范围、土体物理力学性质的变化等多种因素的影响。Chen 等［30］根据摩尔库伦模型提出考虑内摩擦角和黏聚力随温度变化的拟合函数，进而应用强度折减法分析地表温度变化对冻土边坡稳定性的影响。杜东宁［31］以沈阳某基坑工程为例，在弹性矩阵中引入考虑黏聚力、压缩模量和弹性模量的冻融损伤因子，对冻融循环作用下基坑的变形情况展开研究。李国锋［32］提出热-流-力三场耦合的简化算法，确定不同月份下坡体的冻融深度，并采用摩尔库伦模型和以应变为变量的相对安全系数对冻融循环作用下的边坡进行稳定性分析。Subramanian 等［10］以日本北海道地区的坡体为例，基于非饱和土的修正摩尔库伦强度准则，采用极限平衡法对坡体进行稳定性分析，并总结了坡角、降雨/雪量、融雪水量等七种因素对坡体稳定性的影响。Qin 等［33］以新疆某水库为例，创建能描述内摩擦角、黏聚力与滑动面温度之间关系的程序，并通过非饱和土的修正摩尔库伦强度准则和极限平衡法分析了外界温度变化和冻融循环次数对水库岸坡变形情况和长期稳定性的影响。

上述研究为季节冻土区基坑工程的稳定性分析工作提供了重要基础，但仍需进一步完善，主要包括：研究对象主要围绕自然边坡展开，缺少深大基坑的相关研究，冻融作用对季节冻土区基坑稳定性的影响规律尚不明确；基坑稳定性影响因素的相关研究重点围绕温度等环境因素展开，忽略了土体自身不同初始状态等内因的影响；通常采用弹性类或理想弹塑性本构模型进行计算，即只考虑了土体强度和模量等参数在冻融作用下的改变，忽略了土体前期固结压力的显著变化，这导致了坡体应力应变发展情况和稳定性分析结果不够合理。针对上述问题，本文使用考虑冰-水相变的热传导理论确定冻融作用的影响范围，将土体冻融后的物理力学参数赋予基坑受冻融区域，基于考虑黏聚力的修正剑桥模型和强度折减法建立适用于季节冻土区基坑稳定性分析的计算平台，研究冻融前后不同初始状态（本文主要考虑土体的初始干重度）基坑稳定性和位移的变化情况。

1 考虑冻融作用的稳定性分析方法

1.1 冰-水相变热传导理论

采用考虑冰-水相变的热传导方程计算冻融作用的影响范围：

式中：hv为流体热源（W·m-3）；ρ为土体的容重（kg·m-3）；c为比热容（J·kg-1·℃-1）；T为土体的温度（℃）；t为计算时间（s）；λ为导热系数（W·m-1·℃-1）。

1.2 考虑黏聚力的修正剑桥模型

土体作为一类复杂的工程材料，其力学行为不仅具有较强的非线性和弹塑性，还依赖于应力路径和应力历史，故在基坑工程的数值计算中，应根据实际情况选取能反映主要问题的本构模型［34-35］。对于季节冻土区基坑工程，为了反映冻融作用下土体重度、前期固结压力、模量和强度等物理力学参数的变化对土体力学行为的影响，本文选用考虑黏聚力的修正剑桥模型进行力学计算。

在Roscoe 和Burland 提出的修正剑桥模型的基础上，引入黏聚力c，塑性屈服函数可表示为［36］：

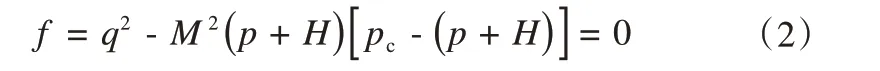
式中：p为平均有效应力；q为偏应力；M为临界状态线斜率；pc为前期固结压力；c为黏聚力；φ为内摩擦角；H=ccotφ。

使用考虑黏聚力的修正剑桥模型时，需定义的模型参数主要包括：临界状态线斜率M、正常固结线斜率λ和回弹曲线斜率κ等［37］。M、λ和κ的几何含义如图1所示，计算公式如下：

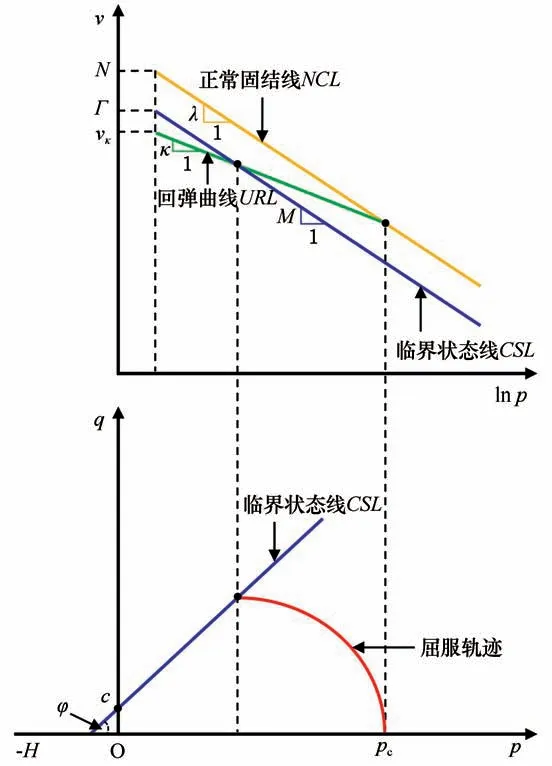
图1 考虑黏聚力的修正剑桥模型Fig.1 Modified cam-clay model considering cohesion

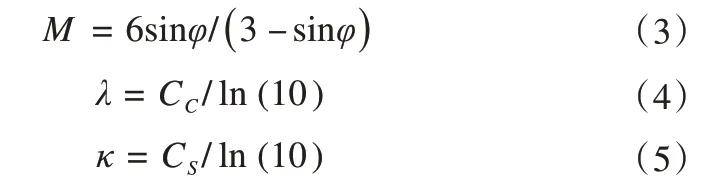
式中：CC为压缩指数；CS为回弹指数。

模型需定义的初始状态参数包括：初始比体积v0和前期固结压力pc。初始比体积v0为正常固结线上p=1 kPa时的比体积：

前期固结压力pc决定了屈服面的初始尺寸，计算公式由屈服方程获得，如式（7）：

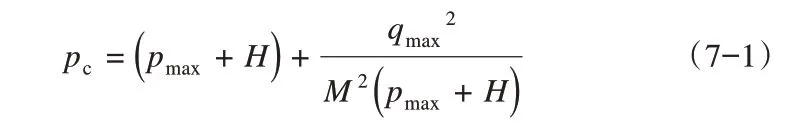
式中：pmax和qmax分别为土体单元的最大平均有效应力和最大偏应力，由竖向应力σv和侧压力系数K0获得：

1.3 强度折减法

本文分别对强度参数中的黏聚力c和内摩擦角φ进行折减，把折减后的c'和φ'重新代入计算，以判断土体是否到达极限平衡状态；若未到达，则继续循环计算至土体到达极限平衡状态，此时的折减系数Fs即为基坑的整体安全系数。具体公式如下：

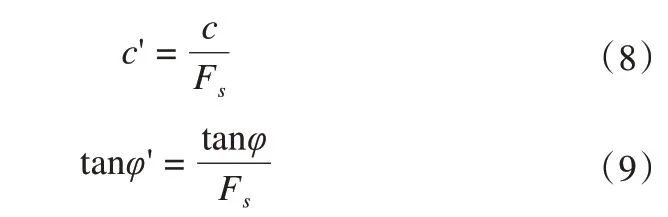
式中：c和φ分别是土体初始的黏聚力和内摩擦角；c'和φ'分别是土体折减Fs后的黏聚力和内摩擦角；Fs为每一次的折减系数。当土体到达临界破坏状态时，Fs即为所求安全系数。

1.4 程序实现

采用FLAC3D 有限差分软件对季节冻土区基坑工程进行数值分析的计算流程主要包括以下三方面：（1）进行热学计算，确定基坑经历冻融作用的区域，即季节冻结层的范围；（2）冻融区域的土体采用冻融后的物理力学参数，未冻融区域的相关参数保持不变；（3）使用强度折减法进行基坑稳定性计算。

2 工程算例

2.1 基坑建模尺寸与支护情况

以场地中心为对称轴，两侧的几何形状、土体性质和边界条件等均相同，不考虑基坑侧壁的差异性，取右幅1∶1 建模。为保证计算精度理想且工程量合理，在开挖深度h为10.0 m 的条件下，模型计算深度取至天然地表以下25.0 m（2.5 h），坑底角至左边界的距离为15.0 m（1.5 h），坑顶角至右边界的距离为35.0 m（3.5 h）。同时根据已有资料数据和初算结果可知部分季节冻土区的最大冻深不足2.0 m，故对基坑地表、侧壁和坑底等重点区域的土层进行网格加密处理。基坑采用桩锚支护体系，即灌注桩+一道预应力锚杆，具体设计为：灌注桩的桩径为1000 mm，嵌固深度为8.0 m，桩间距为1.0 m；预应力锚杆布置在地表以下2.0 m 处，倾角为15°，自由段施加60 kN 的预应力。基坑计算模型如图2。

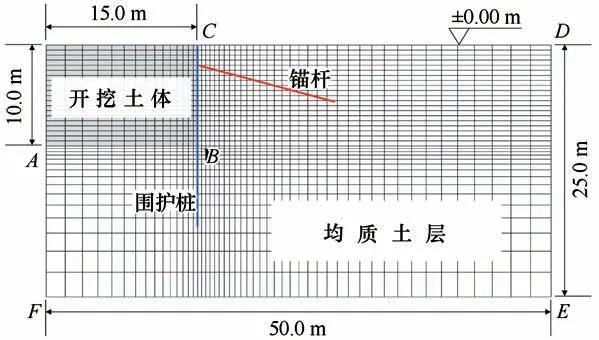
图2 计算模型Fig.2 Numerical model

2.2 计算参数

使用考虑黏聚力的修正剑桥模型进行力学计算，为了反映初始干重度的影响，本文对不同初始干重度的兰州黄土试样在冻融前后分别开展直剪试验和固结试验，获取四种初始干重度条件下兰州黄土冻融前后的相关物理力学参数，见表1。在这些物理力学参数中，c和φ通过直剪试验获取，M通过式（3）求得，λ、κ、pc和v0根据固结试验得到的e-lnp曲线和式（4）～（7）计算获得，具体的试验方法和计算步骤参见《土工试验方法标准》和文献《求前期固结应力的数学模型研究及应用》［38-39］。

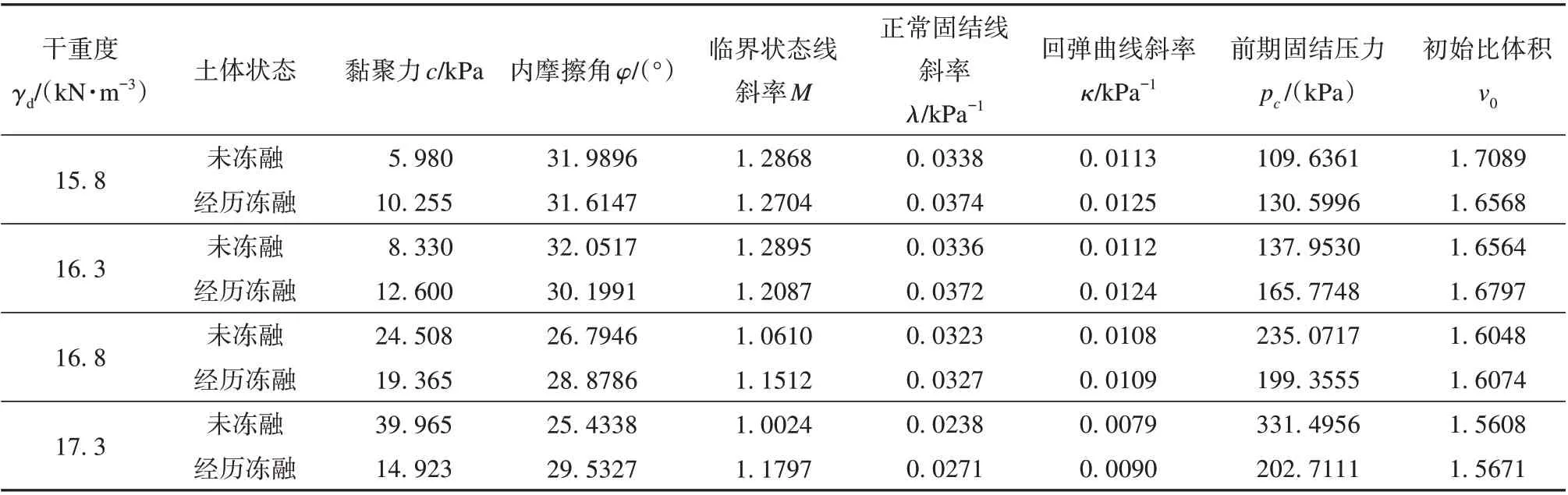
表1 土体物理力学参数Table 1 Physical-mechanical parameters

热学计算部分，土体导热系数和比热容等热学参数通过现有资料确定，具体见表2。

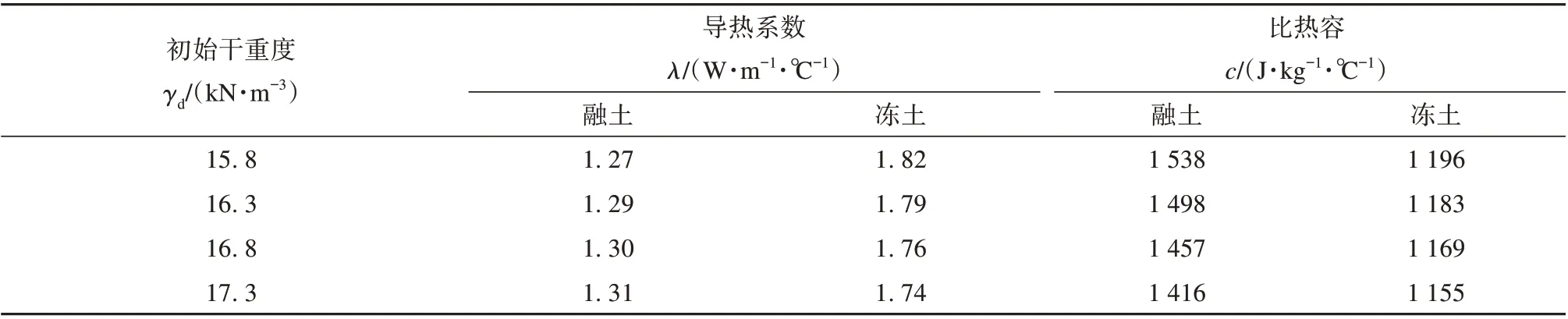
表2 土体热学参数Table 2 Thermal parameters

2.3 边界条件

式中：Ts为下附面层底温度（℃）；Tα为年平均气温（℃），计算中取7.4 ℃；ΔT为附面层温度总增量（℃），天然地表和开挖临空面取2 ℃，基坑底面取1.5 ℃；α为地表温度年增温率（0.02 ℃·a-1）；t为基坑使用时间（s）；s为边界温度条件中一个周期的总时间，以365 天计一年，共计315 636 000 秒；A为下附面层底温度振幅（℃），天然地表和开挖临空面取20 ℃，基坑底面取18 ℃；π/2为计算初始相位（对应一年中温度最高的时间）。计算模型两侧边界（A—F—和D—E—）视为绝热边界。根据土体恒温层深度计算公式求得E—F—边界已处于土体恒温层范围［41］，故计算模型底部的边界温度取为兰州市的年平均温度7.4 ℃。

假设施工场地为半无限大空间，仅考虑基坑在自重情况下的沉降与变形，故图2 计算模型的力学边界条件分别为：A—B—、B—C—和CD——为自由边界，两侧边界沿x方向的位移固定为0，下边界沿x、y、z方向的位移固定为0。

3 结果与分析

3.1 冻融区域与选点说明

根据模拟结果，兰州地区基坑的最大冻深在2.0 m 左右，如图3。由于土体的导热系数和比热容与其干重度有关，因此基坑的冻融区域存在差异：随土体初始干重度的增大而扩大，且主要体现在坑顶和坑底角位置。

图3 不同初始干重度条件下基坑的冻融区域Fig.3 Freeze-thaw regions of foundation trench with different original dry unit weights

图4为围护桩和桩后土体之间水平位移差值随深度变化的曲线，图示结果表明两者间的位移差值在不同深度处基本控制在±0.1 mm 内，满足变形协调关系，故可仅对围护桩的水平位移进行分析。图5 为不同深度处围护桩竖向位移的变化情况，该结果表明桩各节点处的竖向位移值基本相等，不随深度发生显著变化，故可仅对围护桩顶的竖向位移进行分析。

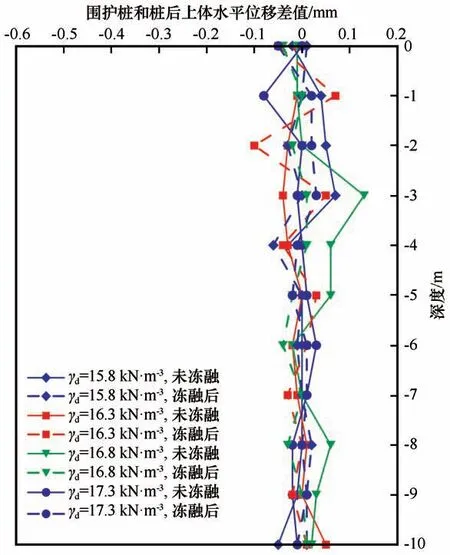
图4 不同深度处围护桩和桩后土体间的水平位移差值Fig.4 Difference of horizontal displacement between pile and soil behind the pile at different depths

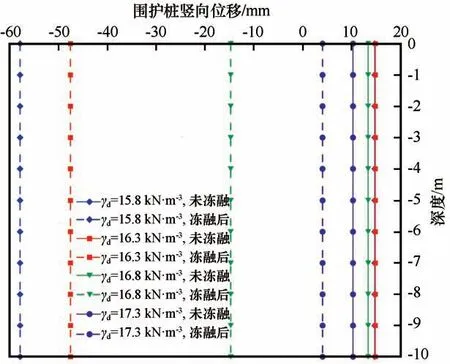
图5 不同深度处围护桩竖向位移变化曲线Fig.5 Curves of vertical displacement of pile at different depths

根据上述讨论和《基坑工程施工监测规程》中基坑监测项目表等规范要求［42］，本文针对4 种不同初始干重度条件下的基坑分别进行冻融前和冻融后的稳定性计算，对比分析不同初始干重度条件下的基坑在冻融前后围护桩水平位移、围护桩顶竖向位移、坑底隆起情况和整体安全系数等指标的变化规律。因此，本文计算基于相同的基坑模型（图2）采用不同的初始干重度和相应的力学参数来反映不同初始状态下冻融作用对基坑稳定性的影响。同时，为方便结果描述，定义下文所述位移的方向均以右、以上为正方向，以左、以下为负方向。

3.2 围护桩水平位移分析

图6描述了不同深度处围护桩水平位移的变化情况。该图表明，未冻融条件下，围护桩的水平位移产生负方向变形，且位移的绝对值随深度增加而减小，并与深度呈线性关系。冻融后，围护桩水平位移保持负方向的变形，且水平位移沿深度方向的发展趋势与土体初始干重度间存在紧密联系。γd=15.8 kN·m-3，16.3 kN·m-3的基坑，冻融后围护桩水平位移的绝对值随深度增加而略有增大，如图7（a）和7（b）；γd=16.8 kN·m-3，17.3 kN·m-3的基坑，冻融后围护桩水平位移的绝对值随深度增加而有所减小，如图7（c）和7（d）。

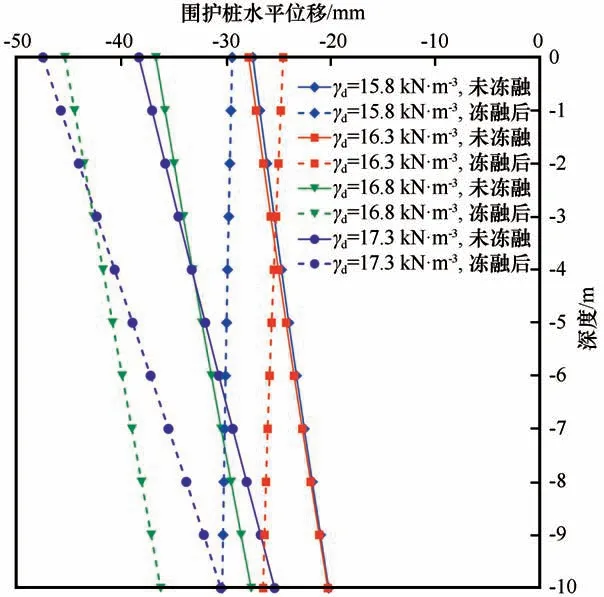
图6 不同深度处围护桩的水平位移Fig.6 Horizontal displacement of the pile at different depths

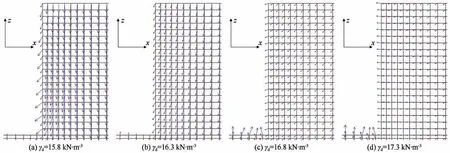
图7 不同干重度条件下桩体冻融后的位移矢量图Fig.7 Displacement vector diagram of the pile after freeze-thaw with different original dry unit weights

与未冻融状态相比，在土体初始干重度γd=16.3 kN·m-3的条件下，基坑围护桩的水平位移在冻融后变化最小；而在其余三种初始干重度条件下，围护桩的水平位移在冻融后变化剧烈。这主要是因为围护桩水平位移在冻融前后的变化规律是由桩后土体的多个物理力学参数在冻融后发生改变而共同产生的。根据前期大量研究表明，对于冻融作用，存在一个临界初始干重度γd0，此时土体的孔隙比、黏聚力、压缩指标和前期固结压力等指标在冻融前后不发生显著变化［4-5，43-45］。本文算例中的兰州黄土，临界干重度γd0接近16.3 kN·m-3，土体冻融前后各项物理力学参数在此干重度附近的变化最小［43］，因此对于土体初始干重度为16.3 kN·m-3的基坑，其围护桩水平位移在冻融前后的变化也达到最小。

3.3 围护桩顶竖向位移分析

图8 为不同初始干重度条件下，围护桩顶竖向位移在冻融前后的变化情况。由图可知，未冻融条件下，基坑开挖导致土体的自重应力释放，围护桩顶的竖向位移略有上升，且上升位移随土体初始干重度的减小而略有增大，但位移值均不超过15 mm，符合现有研究结果和规范要求［46-48］；冻融后，围护桩顶的竖向位移沿负方向发展，且土体的初始干重度越小，竖向沉降越剧烈，当基坑土体的初始干重度γd=15.8 kN·m-3时，沉降量达到最大，为57.8 mm。

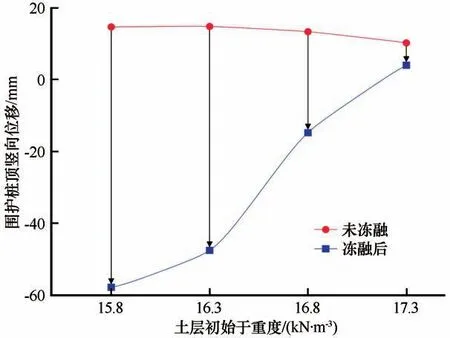
图8 围护桩顶竖向位移变化曲线Fig.8 Curves of vertical displacement of the pile

图8 中两条曲线的差值表明，冻融前后围护桩顶竖向位移的变化量（zp，冻融后－zp，未冻融）随土体初始干重度的减小而显著增大，即随着干重度的减小，冻融后桩体的竖向沉降越明显。γd=15.8 kN·m-3的基坑，围护桩顶竖向位移冻融前后的变化量超过70 mm，沉降变形剧烈；而γd=17.3 kN·m-3的基坑，其变化量小于10 mm，围护桩在冻融后的沉降较小，仍有轻微上升变形。这说明较小的土体干重度对桩的竖向位移影响较大。出现该变化的原因主要在于土体的正常固结线斜率λ在冻融后增大（表1），土体更易发生沉降固结，桩体也随之发生较大的下沉变形。

3.4 坑底隆起分析

图9 为不同初始干重度条件下，坑底隆起位移在冻融前后的变化情况。结果表明，随着初始干重度的增大，坑底隆起的位移量在冻融前后均表现出先增大后减小的趋势。

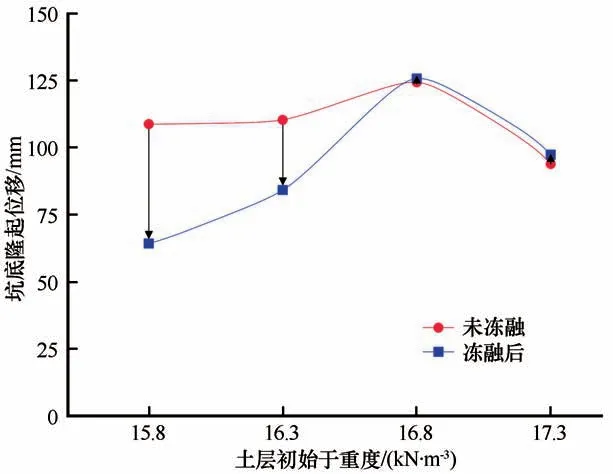
图9 坑底隆起位移变化曲线Fig.9 Curves of basal heave

比较图9 的两条曲线可以看出，冻融前后坑底隆起位移的变化量（zb，冻融后－zb，未冻融）随初始干重度的增大表现出先减小而后略有增大的趋势。初始干重度较小的土体，冻融后基坑抵抗隆起的能力提升，坑底隆起位移显著下降。如γd=15.8 kN·m-3和γd=16.3 kN·m-3的基坑，其坑底隆起位移分别从108.8 mm 和110.4 mm 下降至64.3 mm 和84.2 mm，下降幅度最大可至40%。而土体初始干重度较大（γd=16.8 kN·m-3，17.3 kN·m-3）的基坑，冻融后抵抗隆起的能力有所下降，坑底隆起位移略有增大。上述变化结果说明，基坑经历冻融后，较小的初始干重度对坑底隆起位移能起到一定的抑制作用。

3.5 基坑的安全系数

基于本文建立的计算平台，获得不同初始干重度条件下基坑冻融前后的整体安全系数，计算结果均为1.00625。该结果表明，在桩锚支护体系的作用下，基坑浅层土体的冻融基本不影响基坑的整体稳定性。对于开挖深度为10 m，冻融深度为2 m 的季节冻土区基坑，围护桩8 m 的嵌固深度和地表以下2 m 处的锚杆布置保证了支护结构的作用范围，对冻融区域起到了有效的加固作用。基坑的整体安全系数因此不受影响。

本文的研究重点在于考虑冻融作用对不同初始干重度基坑稳定性的影响规律。为了排除多层土体物理力学性质存在的差异性对研究结果产生影响，本文在基坑稳定性的计算分析中采用了初始状态均一的土体，以分析不同初始干重度对基坑冻融前后变形和稳定性的影响规律和趋势。由于在本文计算中仅考虑了均一的土层属性，因而在实际工程当中很难找到与之对应的实测数据对计算结果进行验证。如文中2.2 节所述，本文计算采用的参数均是依据实际的冻融试验和相关的力学试验获取，由此计算得到的不同初始干重度条件下基坑冻融前后变形和稳定性的影响规律和趋势仍然对实际工程具有一定的指导和借鉴意义。

4 结论

本文根据考虑冰-水相变的热传导理论、考虑黏聚力的修正剑桥模型和强度折减法建立了适用于季节冻土区基坑稳定性分析的计算平台，并结合具体试验数据分析了冻融前后不同初始干重度条件下基坑局部变形和整体稳定性的变化规律，得到以下结论：

（1）冻融作用加剧围护桩水平位移向临空面发展，且存在一个临界干重度γd0，在该初始干重度附近时，围护桩水平位移在冻融前后的变化量较小；土体的初始干重度远离该临界值后，围护桩水平位移的变化量随之增大。

（2）冻融后，围护桩顶竖向位移开始沿负方向发展，且土体初始干重度越小，桩顶竖向位移的变化量（zp，冻融后－zp，未冻融）越大，竖向沉降变形越明显。

（3）初始干重度越小，冻融前后坑底隆起位移的变化量（zb，冻融后－zb，未冻融）越大，坑底隆起位移显著下降；而初始干重度较大的基坑，坑底的隆起位移量在冻融后略有上升。即冻融后，较小的初始干重度在一定程度上缓解了坑底的隆起变形。

（4）冻融作用对桩锚支护基坑局部位移的影响较大，且土体的初始干重度是重要影响因素之一。基坑冻融前后竖向的位移变形情况具有一致性，即初始干重度越小，围护桩顶位移和坑底隆起位移在冻融后的变化越显著。

（5）由于桩锚支护的作用，季节冻土区基坑的安全系数在冻融作用下未发生改变，浅层土体的冻融不影响基坑的整体稳定性。