二自由度电磁轴承转子系统的动力学分析

陈淑婕 李欣业 张华彪 张利娟

摘要 根据麦克斯韦电场理论得到的电磁力模型并结合PD控制理论，在差动激磁方式下建立了二自由度电磁轴承转子系统的动力学方程。基于多尺度法对泰勒展开后的方程进行摄动分析，求得了关于系统振幅和相位的平均方程。利用同伦延拓法对平均方程进行求解，得到了系统的幅频特性曲线，发现幅频特性曲线表现出明显的滞后现象，在升速和降速通过共振区域时都会发生跳跃，利用数值仿真对解析计算的正确性进行了验证。分析了电流及控制参数对幅频特性曲线的影响，研究表明共振区域的最大振幅及其对应转速随着电流的增大而增大，随比例系数的增大而减小。

关 键 词 电磁轴承转子系统;非线性动力学;PD控制;多尺度法;数值仿真

中图分类号 O322     文献标志码 A

Abstract According to the electromagnetic force model obtained by Maxwell's electric field theory and PD control theory， the dynamic equation of the two-degree-of-freedom electromagnetic bearing rotor system is established under differential excitation mode. The perturbation analysis of Taylor's expanded equations is based on the method of multiple scales， and the average equations for the amplitude and phase of the system are obtained. Using the homotopy continuation method to solve the average equation， the amplitude-frequency characteristic curve of the system is given. It is found that the amplitude-frequency characteristic curve shows obvious hysteresis， and jumps occur when the speed is increased and the speed is reduced. The simulation verified the correctness of the analytical calculation. The influence of current and control parameters on the amplitude-frequency characteristic curve is analyzed. The results show that the maximum amplitude of the resonant region and its corresponding rotational speed increase with the increase of current， and decrease with the increase of the proportional coefficient.

Key words active magnetic bearing rotor system; nonlinear dynamics; PD control; the method of multiple scales; numerical simulation

0 引言

電磁轴承（Active Magnetic Bearing，AMB）具有无接触、无润滑、允许转子高速旋转、功耗低、维护成本低且寿命长[1-2]等优点，从而得到了越来越广泛的应用。但是由于电磁轴承转子系统固有的非线性，使其表现出非常复杂的动力学特性。所以电磁轴承转子系统的非线性动力学及其控制问题一直备受研究者的关注。

Schweitzer 等[1]系统地介绍了主动磁轴承的基本原理、总体结构以及各组成部分的设计方法，为后面的研究奠定了理论基础;魏金强[3]以五自由度磁悬浮轴承为研究对象，设计了系统的主要电磁参数，并对传统算法和模糊PID控制进行了研究，最终实现了模糊PID控制算法，满足了系统的控制要求，实现了系统的精确控制;Ji等[4]研究了主动磁电磁轴承转子系统的非线性响应问题，利用多尺度方法对其进行了摄动分析，结果表明，稳态解通过鞍结点分岔或Hopf分岔失去稳定性。李泽辉等[5]以自行设计的磁悬浮储能飞轮测试样机以径向磁悬浮轴承为例，应用ANSYS有限元分析软件对径向磁悬浮轴承磁路进行仿真与计算;安华贞等[6]研究了电磁轴承的非线性振动，利用牛顿定律对电磁轴承转子系统进行了动力学建模，由于非线性项的影响，系统出现了正规、椭圆、准周期等运动类型;文献[7]基于四极对模型和PID控制研究了径向电磁轴承的可控性问题;王媛[8]研究了电磁轴承转子系统的非线性动力学特性，建立了转子系统的运动方程并进行了数值仿真，结果得到了转子中心轨迹图、相应的时间历程图、分岔图及Poincaré映射图。展示了电磁轴承转子系统的周期解、准周期解等非线性动力学行为;虞烈等[1]系统介绍了轴承转子系统动力学的基本理论及其在工程中的应用，内容涉及了单跨单质量转子轴承系统、多跨多质量转子轴承系统、多平行轴系统和电磁轴承转子系统等;刘熙娟[9]针对一类电磁轴承-刚性转子系统，研究了它在某些参数区域中出现的Hopf分岔、全局分岔等动力学现象。对转子系统在局部处的动力学特征进行了定性、定量的研究。通过中心流形定理，对四维高阶系统进行降维操作得到了二维降阶系统。利用范式理论对该降维系统进行分析，发现该轴承-转子系统在局部处发生了超临界Hopf分岔。对系统进行数值模拟得到分岔图，验证了理论分析的正确性。张海燕[10]研究了电磁轴承转子系统的非线性动力学，发现了电磁轴承转子系统在某些参数区域内出现全局分叉和混沌运动情况。季进臣等[11]对高速不平衡刚性转子在应急情况下跌落在保持轴承内的非线性动力学进行了研究，数值分析了转子的瞬态响应，给出了跌落过程中转子在保持轴承中的轨迹、滑动涡动阶段的速度和功率损耗。

本文利用非线性动力学理论对电磁轴承转子系统进行了分析，运用PD控制理论对电磁轴承转子系统的非线性振动进行控制研究，并利用多尺度法对无量纲化后的运动微分方程进行求解，得到平均方程，再利用同伦延拓法对平均方程进行稳定性分析，最终得到解的幅频特性曲线。将利用MATLAB对无量纲化后的运动微分方程求解得到的幅频特性曲线与利用多尺度法及同伦延拓法求解得到的幅频特性曲线作对比，发现数值仿真的结果与理论分析的结果相吻合，证明了理论推导的正确性。同时分析了电流和控制参数对幅频特性曲线的影响。以及共振区域最大振幅和最大振幅对应的转速与电流和控制参数的关系。

1 两自由度电磁轴承转子系统的动力学模型

对如图1所示结构的电磁轴承，定子端面横截面极性相同，称为同极磁极。这种结构的优点是磁极周围的磁场变化较小，从而使涡流的变化减小因而无需使用叠片，这便使得这种轴承可应用于由于某些原因不能使用叠片的场合。图2为磁铁的电磁力示意图。

1.1 电磁力模型

电磁轴承转子系统是一个集机、电、磁一体化的综合系统，电磁力的计算涉及磁场和磁路。磁铁的吸引力产生在具有不同导磁率的界面上，这些力的计算以磁场能量为基础。在闭合系统中，力f可由虚位移原理导出：

在建立模型之前，先将转子作为集中质量处理、忽略绕组漏磁、忽略铁芯和转子中的磁阻即认为磁势均匀降落在气隙上并且忽略磁性材料的磁滞和涡流。

根据电磁理论，通过每一个磁极产生的电磁力[fm]可以表示为

1.2 基于PD（Proportional-Differential）控制的电磁轴承转子系统的动力学方程

本文采用的是PD控制，控制电流可以表示为

式中：[kp]为比例控制系数;[kd]为微分控制系数。由比例控制所提供的电磁力起着抵消原位移负刚度的作用，并使系统在被矫正后具有一定的正刚度;微分控制部分相当于向系统提供正阻尼，从而使系统具有足够的稳定性。

作用在每个磁极上的电磁力是电磁轴承内侧的磁铁的吸引力。根据图1电磁轴承转子受力示意图可知，在[x]方向和[y]方向的电磁力的表达式为

2 近似解析分析

由于电磁轴承转子系统动力学特性的非线性微分方程非常复杂。对它的高阶非线性动力学方程只能求得高精度的数值解。但是数值解是不能完全代替近似解析解的，所以摄动分析方法成了研究非线性方程的重要工具。根据多尺度法，选择1∶1的共振比情况进行研究和分析，设式（8）的解为

图3是由多尺度法和同伦延拓法相结合得到的幅频特性曲线，图中实线代表稳定解，虚线代表不稳定解。图4给出了根据无量纲化后得到的运动方程进行数值求解所得到的结果。通过图4可以发现，当转子转速从低速逐渐上升时，如图中实线箭头所示，转子的振幅由缓慢上升到加速上升，当达到一定值时发生跳跃现象，最终振幅趋于零，系统处于单稳态。同理，当转子转速从高速逐渐降低时，如图中虚线箭头所示，转子的振幅开始缓慢增大，之后增大速度加快，达到一定值时，系统从双稳态区域进入单稳态区域，振幅逐渐趋于零。比较图3与图4，可以看出两者吻合较好。

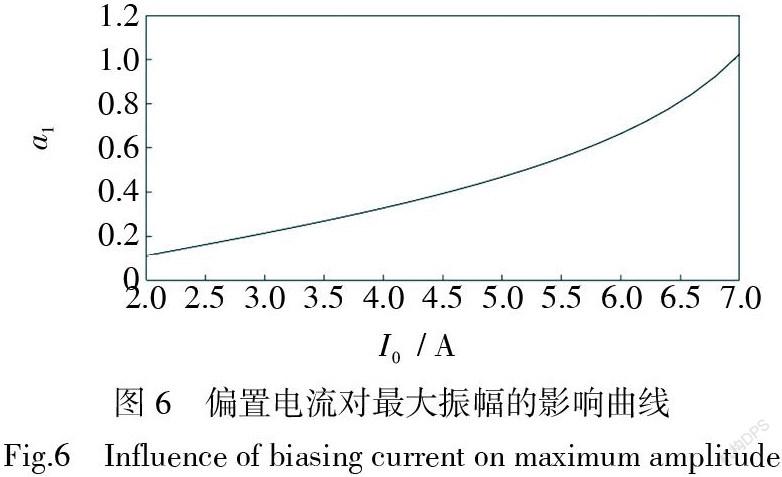
偏置电流对电磁轴承转子系统振动性能的影响如图5所示。从图5中可以看出，减小偏置电流会使系统在较低的转速下发生共振，但共振区域的最大振幅相对较小，系统双稳态区域较小。反之增大偏置電流，会使系统在高转速下出现共振，且共振区域的最大振幅相对较大，双稳态区域也随之增大。随着偏置电流的增大，共振区域的最大振幅对应的转速[np]也随之上升。图6和图7为偏置电流对共振区域的最大振幅和最大振幅对应的转速的影响曲线。由图可知，随着偏置电流的增大，共振区域的最大振幅和最大振幅对应的转速也随之增大。

比例系数对电磁轴承转子系统动态性能的影响如图8所示。从图中可以看出随着比例系数的增大共振区域逐渐减小，共振区域的最大振幅和最大振幅对应的转速都随之减小。增大比例系数使系统在转速低的情况下发生共振，共振区域减小。反之，减小比例系数使系统在较高的转速下发生共振，共振区域的最大振幅增大，共振区域增大。图9和图10为比例系数对共振区域的最大振幅和最大振幅对应的转速的影响曲线。由图可知，随着比例系数的增大，共振区域的最大振幅和最大振幅对应的转速随之减小。

3 结论

本文基于二自由度电磁轴承转子系统的动力学方程，利用多尺度法对泰勒展开后的无量纲运动方程进行摄动分析，求得了关于系统振幅和相位的平均方程。利用同伦延拓法对平均方程进行求解，给出了系统的幅频特性曲线，发现幅频特性曲线表现出明显的滞后现象，在升速和降速通过共振转速时都会发生跳跃，利用数值仿真对解析计算的正确性进行了验证。验证结果表明数值计算的结果与解析解相吻合。研究了偏置电流和比例系数对幅频特性曲线的影响，结果表明在其他参数一定的情况下，随着偏置电流的增大，共振区域的最大振幅和最大振幅对应的转速随之增大。随着比例系数的增大，共振区域的最大振幅和最大振幅对应的转速随之减小。

参考文献：

[1]    SCHWEITZER G. 主动磁轴承基础、性能及应用[M]. 虞烈，袁崇军，译. 北京：新时代出版社，1997.

[2]    SIVA SRINIVAS R，TIWARI R，KANNABABU C. Application of active magnetic bearings in flexible rotordynamic systems-A state-of-the-art review[J]. Mechanical Systems and Signal Processing，2018，106：537-572.

[3]    魏金强. 磁悬浮轴承控制系统研究[D]. 武汉：武汉理工大学，2007.

[4]    JI J C，HANSEN C H. Non-linear oscillations of a rotor in active magnetic bearings[J]. Journal of Sound and Vibration，2001，240（4）：599-612.

[5]    李泽辉，滕万庆，李翀. 磁悬浮储能飞轮用径向磁轴承磁路仿真分析[J]. 储能科学与技术，2014，3（4）：308-311.

[6]    安华贞，杨晓东，张伟. 八极电磁轴承的非线性动力学研究[C]//第十六届全国模态分析与试验学术会议论文集. 天津，2016：130-132.

[7]    SHELKE S. Controllability of radial magnetic bearing[J]. Procedia Technology，2016，23：106-113.

[8]    王媛. 电磁轴承—转子系统的动力学行为分析[D]. 西安：西安理工大学，2009.

[9]    刘熙娟. 电磁轴承—转子系统的分岔研究[D]. 兰州：兰州交通大学，2016.

[10]  张海燕. 电磁轴承-转子系统的非线性动力学[D]. 北京：北京工业大学，2002.

[11]  季进臣，虞烈. 电磁轴承转子系统中高速不平衡转子跌落过程的非线性动力学[J]. 机械工程学报，1999，35（5）：62-66.

[12]  CHINTA M，PALAZZOLO A B. Stability and bifurcation of rotor motion in a magnetic bearing[J]. Journal of Sound and Vibration，1998，214（5）：793-803.

[13]  胡業发，周祖德，江征风. 磁力轴承的基础理论与应用[M]. 北京：机械工业出版社，2006.

[14]  胡磊. 电磁轴承及其控制系统的研究与设计[D]. 沈阳：沈阳工业大学，2017.

[15]  KASARDA M E F，ALLAIRE P E，NORRIS P M，et al. Experimentally determined rotor power losses in homopolar and heteropolar magnetic bearings[J]. Journal of Engineering for Gas Turbines and Power，1999，121（4）：697-702.

[16]  JI J C. Stability and Hopf bifurcation of a magnetic bearing system with time delays[J]. Journal of Sound and Vibration，2003，259（4）：845-856.

[17]  胡海岩. 应用非线性动力学[M]. 北京：航空航天出版社，2000：57-59.

[18]  虞烈. 可控磁悬浮转子系统[M]. 北京：科学出版社，2003：37-61.

[19]  刘熙娟，刘云，褚衍东，等. 一类轴承转子系统的全局动力学行为分析[J]. 东北师大学报（自然科学版），2017，49（3）：22-28.

[20]  刘习军，贾启芬. 工程振动理论与测试技术[M]. 北京：高等教育出版社，2004：11-33.

[21]  谢振宇，徐龙祥，李迎，等. 磁悬浮轴承转子系统的稳定性及动态特性分析[J]. 机械科学与技术，2004，23（7）：765-767，770.