倾斜挡墙黏性填土非极限主动土压力计算
陈建旭,钱 波,郭 宁,余明东,庄锦亮
(西昌学院 土木与水利工程学院,四川 西昌 615013)
1 研究背景
土压力问题作为土力学的三大经典问题之一,一直倍受界内人士的广泛关注,如何能够将土压力理论更好的指导工程实践,是人们需要解决的问题。为此,大量学者对土压力展开了研究。
Sherif等[1]、Fang等[2]、周应英等[3]、杨斌等[4]通过室内模型试验发现,无论是黏性土还是砂土,土压力大小均受墙体位移量的影响,且呈非线性分布。Chang[5]在模型试验基础上,建立了砂土位移量与内、外摩擦角的线性关系,得到了改进的库仑主动土压力计算公式。卢坤林等[6]通过三轴卸荷试验类比于墙体位移与土压力的关系,得到了砂土内摩擦角随位移变化的表达式,基于条分法得到了非极限主动土压力的分布解。应宏伟等[7]、吴明等[8]、陈建旭等[9]通过薄层单元法,并考虑了土拱效应,得到了砂土位移达到极限时的主、被动土压力计算公式,与相关试验较为吻合。彭明祥[10]、刘杰等[11]则分别通过极限平衡法及极限塑性上限理论得到了黏土的最大裂缝深度以及土压力分布的计算公式。王奎华等[12]基于变分法推导了极限状态下黏性填土土压力合力的计算公式。陈建功等[13]弥补了已有变分法求解黏性土主动土压力未考虑张拉裂缝的缺陷。涂兵雄等[14]、王学民等[15]基于朗肯滑裂面,假定产生圆弧形土拱,求解了墙背铅直或倾斜情况下的黏土的主动土压力,赵琦等[16]进一步将此方法运用到有限黏土的土压力计算。徐日庆等[17-18]以黏性土的摩尔应力圆,通过平移坐标轴的方式,建立了黏性土位移与内摩擦角的关系,并将此推广到了有限黏土的土压力计算。娄培杰[19]同时考虑了土拱效应和位移的影响,推导了黏土的非极限主动土压力计算公式。
实际工程中涉及到黏土的工程较多,因而,黏性填土的土压力理论应用范围更广。但目前对黏土的土压力研究存在一定的不足:文献[10]—文献[13]未考虑墙体位移的影响,文献[14]—文献[17]忽略了土拱效应的影响,这与试验[3-4]结果不符;对黏土滑裂面假定为朗肯滑裂面[14-16]或库仑滑裂面[17-19],事实上朗肯滑裂面并不适应于倾斜粗糙墙背,且土体未达到极限位移的情况,库仑滑裂面不适用于黏性填土及墙背与填土存在粘着力的情况;文献[14]—文献[19]先通过得到主动土压力的解答才能得到裂缝深度的大小,这其实存在逻辑上的错误,是裂缝深度的改变影响土应力的大小,而不是相反;文献[14]—文献[15]、文献[17]、文献[19]中的边界条件并不满足受力微分方程,这主要是由于未考虑张拉裂缝所产生的零应力区所导致的。
综上所述,黏性土压力理论仍有待进一步研究,本文在前人的基础上,将墙后黏性填土滑裂体分为弹性区和塑性区两部分来研究,并基于非极限状态下的虚功原理,建立了能量守恒方程,推导了张拉裂缝深度及潜在滑裂面的解析式。在此基础上,考虑了土拱效应,由水平层分析法推求了倾斜挡墙(包括仰斜式,直立式、俯斜式)黏性填土非极限主动土压力分布、合力大小、合力作用点深度的理论公式,并将其与相关模型试验进行了对比分析,使推导过程在逻辑上更为严谨,使所得土压力值更趋近于实际。
2 理论推导
本文理论分析满足以下假定:①墙体的刚度足够大,不会发生弯曲变形;②墙后黏土属于各向同性的弹塑性材料;③墙后黏土及黏土与墙背间的抗剪强度满足摩尔-库伦准则;④墙土黏聚力与内、外摩擦角随位移变化的规律相同。
2.1 位移与摩擦角、黏聚力的关系
合理确定黏性填土内摩擦角、墙土黏聚力、墙土摩擦角(外摩擦角)、墙土黏聚力是计算土压力的关键。然而实际工程中,墙体允许发生的位移量往往较小,此时,墙后填土也并未达到其极限位移值,内摩擦角发挥值φm与墙体位移比η存在如下关系[17-19],即
(1)
其中,T=(1-Rf+ηRf)(1+sinφ) 。
式中:η=S/Sa,S为墙体位移,Sa为填土的极限位移值,其值一般为墙高的0.4%~1%;φ为土体达到极限位移时所对应的内摩擦角,可由试验测得;Rf为破坏比,取值范围在0.75~1之间,无实测资料时可取0.85;K0为静止土压力系数,针对黏性土,Federico等[20]通过统计分析59例静止土压力实测值,满足如下关系,即
K0=[1-sin(0.64φ)]/[1+sin(0.64φ)] 。(2)
Fang等[2]通过试验发现外摩擦角与位移近似呈线性关系,Chang[5]建立了外摩擦角发挥值δm与位移的关系式,即
tanδm=tanδ0+η(tanδ-tanδ0)。
(3)
式中δ、δ0分别对应墙体达到极限位移时、墙体静止时的外摩擦角。无实测资料时,δ0可取φ/2,δ则取2φ/3。
对于填土黏聚力发挥值cm、墙土黏聚力发挥值cwm的选取,按照俆日庆等[17]的假定,其表达式为
(4)
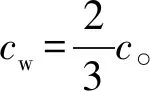
2.2 张拉裂缝、滑裂面的确定
建立如图1(a)所示的计算模型,墙高为H,墙后填土水平,重度为γ,且受到均布超载q0,墙背倾角为ε,当ε<0°时,为仰斜式;当ε=0°时,为直立式;当ε>0°时,为俯斜式。墙后潜在滑裂面倾角为βm,滑裂体所产生的张拉裂缝深度为y0m,即BC以上土体对墙体将不产生侧向压力,可作为弹性土体覆盖在塑性区ABC上,并可等效为γy0m的均布超载作用。此时的均布超载q为q0与γy0m之和(见图1(b))。
墙体在土压力的作用下将背离填土发生一定量的位移而处于平衡状态。以墙挡墙和填土为研究对象,根据虚功原理,可对其虚设一个位移(此位移并非墙体发生的实际位移量),取单位时间,则存在一个虚速度Vw。如图1(b)所示,若土体满足摩尔-库伦破坏准则,则根据相关联流动法则,墙后填土塑性区ABC将产生一个方向与潜在滑裂面AC呈斜向下且角度为φm的速度Vs,由于AB面为墙体与填土的速度间断面,存在一个相对速度Vsw,其方向与墙背呈斜向下且角度为δm,则Vw、Vs、Vsw可构成一个速度矢量三角形,由正弦定理,满足下列关系:
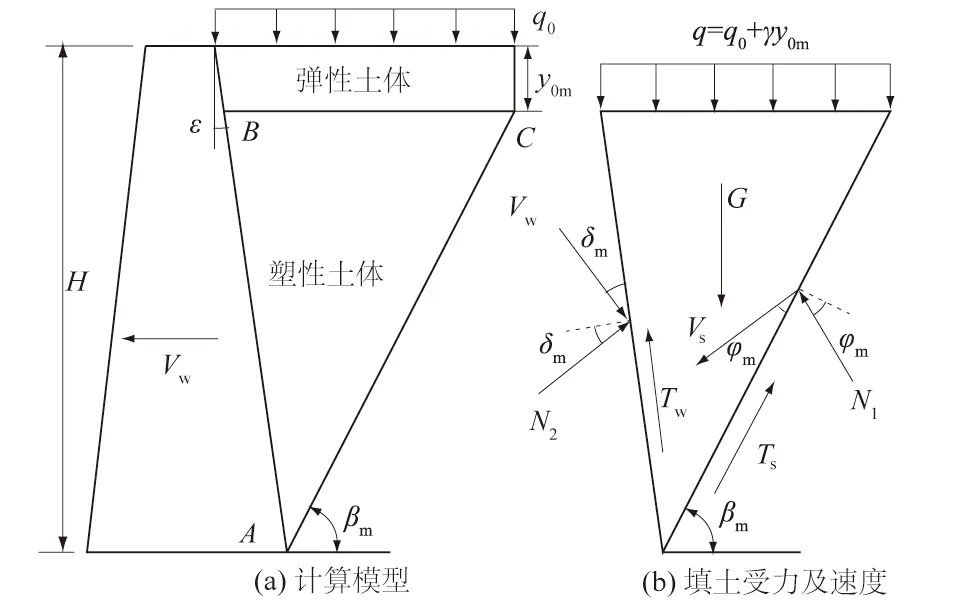
图1 非极限状态理论分析模型示意图Fig.1 Schematic diagram of non-limit state theoretical analysis model
(5)
单独将塑性区ABC作为研究对象,则由虚功原理知,其外力所作的功(单位时间的外力所作功则为功率)应为0。
2.2.1 外力零功率
图1(b)中滑裂面AC受到的力N1为AB面正应力与其所产生的摩擦力的合力,其方向与滑裂面法线所呈夹角为φm,则Vs⊥N1,同理Vsw⊥N2,即可得到外力N1、N2的功率为0。
2.2.2 外力正功率
通过图2(b)外力与速度的关系,重力G与均布超载q做正功,则对应功率为PG和Pq,即:
(7)
2.2.3 外力负功率
通过图1(b)外力与速度的关系,AB面与AC面由黏聚力所产生的剪应力Tw与Ts作负功,则对应功率为PTw和PTs,即:
(8)
(9)
2.2.4 能量守恒方程
由虚功原理可得
PG+Pq+PTw+PTs=0 。
(10)
将式(5)—式(9)代入式(10),并考虑到塑性区在B点就会产生,则H趋近于y0m时,取H=y0m,并代入式(10),可求得y0m,即
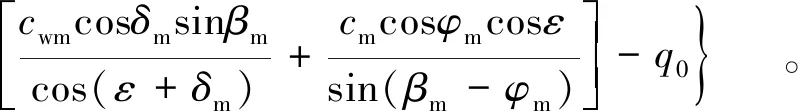
(11)
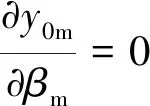
(12)
其中J=cwmcosδm/[2cmcosφmcos(ε+δm)],K=Jcos2φm+cos(φm+ε),L=[Jsin2φm+sin(φm+ε)]2。
存在一个临界超载q′ 满足如下关系式,即
(13)
当q0≥q′时,填土将不再产生张拉裂缝,此时y0m=0。
当ε=δ=0°,cwm=q0=0 kPa,η=1时(满足朗肯假设),则:
所求裂缝深度y0m、滑裂面倾角βm与朗肯解完全一致,即朗肯解为本文的特解。
2.3 土拱效应分析

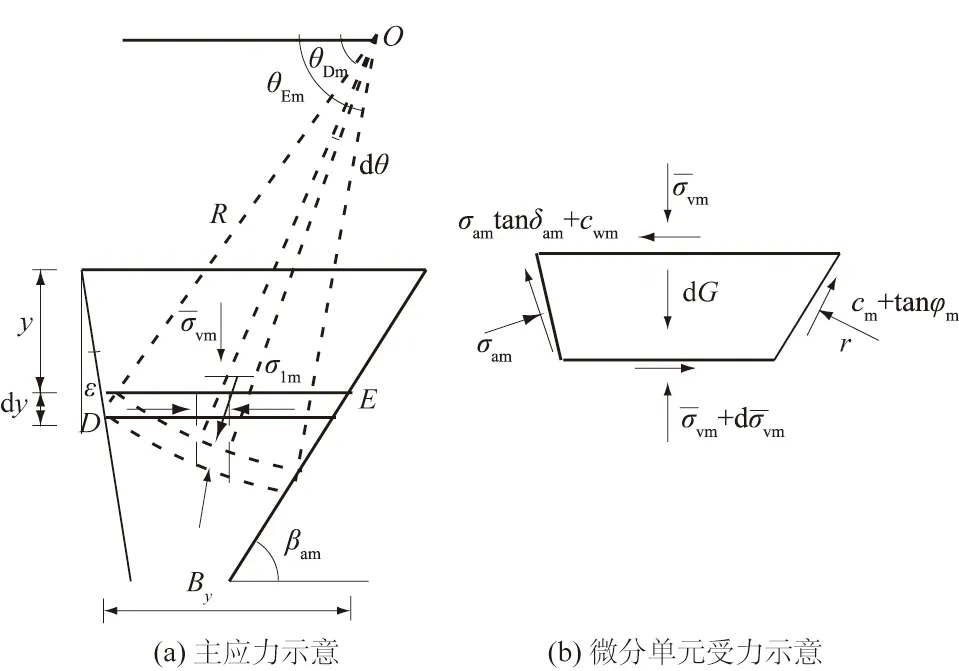
图2 非极限状态应力分析示意图Fig.2 Schematic diagram of stress analysis in non-limit state
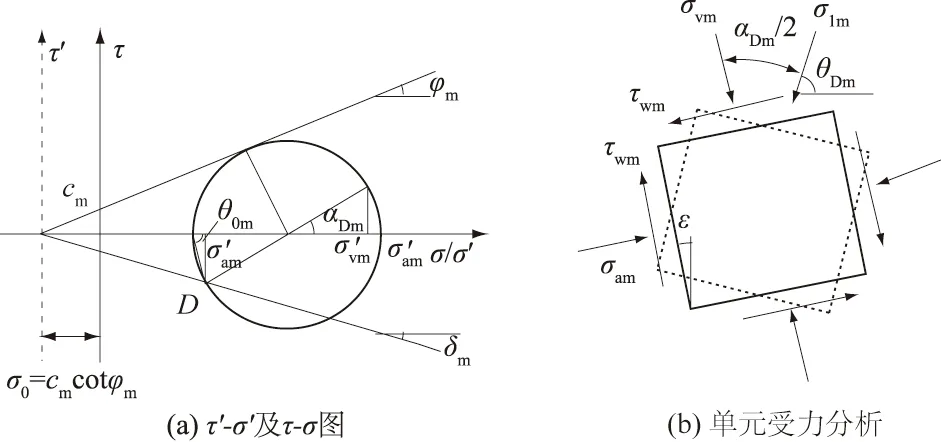
图3 非极限状态下墙后黏性填土摩尔应力圆Fig.3 Mohr stress circle of cohesive soil behind wall under non-limit state
如图2(a)所示,小主应力轨迹线为曲线,可假定为圆弧形[7-9,14-16,18-19],土拱半径为R,则任意土层DE的长度By为
By=R(cosθDm-cosθEm) 。
(15)
式中θDm、θEm分别为D点处和E点处的大主应力与水平面的夹角。可根据图3的几何关系求出θDm为
θDm=π/2-αDm/2+ε。
(16)
式中αDm为D点处的大主应力偏转角,可根据摩尔应力圆求得,即
αDm=arcsin(sinδm/sinφm)-δm。
(17)
大主应力与滑裂面的夹角为π/4-φm/2,则滑裂面上任意点E与水平面的夹角为
θEm=π/4-φm/2+βm。
(18)
由于研究对象为黏土,可将图3应力圆中的纵坐标向左平移若干单位,使之与研究砂土类似,平移量σ0为
σ0=cmcotφm。
(19)
则在新坐标系τ′-σ′中,微分单元DE中任意点处的水平应力σ′hm和竖向应力σ′vm分别为
(20)
式中θ为塑性区ABC中任意点的大主应力与水平方向的夹角。


(22)
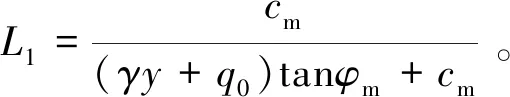

由式(22)可以看出,当填土为砂土时,cm=0,其侧土压力系数为K′m,其值为
则黏性填土侧土压力系数Km与无黏性土侧土压力系数K′m满足下列关系,即
(24)
2.4 微元受力平衡分析
水平微元受力分析如图2(b)所示,可建立水平方向平衡方程为
σamdy-(σamtanδm+cwm)tanεdy+
(rtanφm+cm)cotβmdy-rdy=0 。
(25)
竖直方向平衡方程为
σamtanεdy+(σamtanδm+cwm)dy+(rtanφm+
(26)
式中dG为微元的重力,其值为dG=γ(H-y)(tanε+cotβm)dy。

(27)
中间变量X,Y分别为
(28)
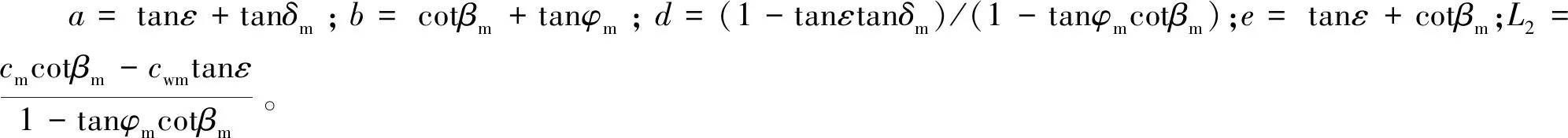
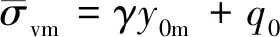
(30)
则法向应力σam为
(31)
合力大小Eam为
[(H-y0m)2-(H-H1m)2]+
(32)

式中H1m为墙顶至墙底0应力区的高度,比H略小,主要是由于黏聚力作用导致墙底可能会产生极小部分的零应力区,其值可通过令式(31)为0得到。
当ε=δ=0°,cwm=q0=0 kPa,η=1时(满足朗肯假设),则式(32)可化为
(33)
此时与朗肯理论所得到的合力公式一致,究其原因,微元受力平衡分析是以前文所推导的张拉裂缝深度y0m及滑裂面βm为前提,而满足朗肯假设时,其y0m与βm与朗肯解一致,并且本节所推导的土拱效应作为土层的内力分析,仅会改变土压力分布,并不会改变其合力。
倾覆力矩M为
[(H-y0m)2-(H-H1m)2] 。
(34)
则合力作用点深度ham为
(35)
3 试验对比验证
3.1 试验1
周应英等[3]选取模型尺寸为5.5 m×2 m×4.45 m(长×宽×高)的装土箱进行试验,试验槽为钢结构。为保证其刚性要求,在墙背上安置刚弦式和电阻应变式压力盒,自上而下,相间排列,进行土压力的测定,以减小偶然误差。其他参数为:γ=14.27 kN/m3,φ=24.3°,δ=21.4°,c=1.472 kPa,cw=0.98 kPa,Sa=3.94 cm,q0=0 kPa,Rf=0.85,ε=0°。图4为非极限主动土压力分布理论解与试验值对比,经计算,当S=0 cm时,βm=47.74°,y0m=0.21 m;当S=3.94 cm时,βm=52.47°,y0m=0.41 m。可以看出,位移对土压力分布的影响较大,且均呈非线性分布,而朗肯理论不能考虑位移影响,与试验值相差较大,本文同时考虑了位移、墙背粗糙、土拱效应的影响,所得到的理论解与试验值能够大致吻合。
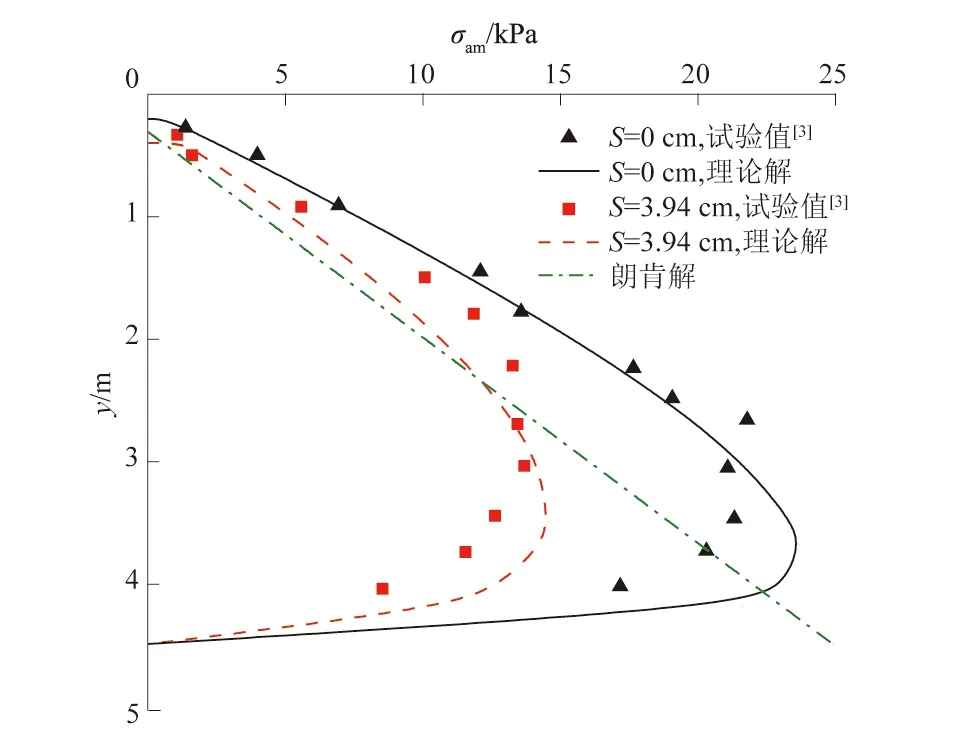
图4 非极限主动土压力分布理论解与试验值[3]对比Fig.4 Comparison of non-limit active earth pressure distribution between theoretical solution and experimental value[3]
3.2 试验2
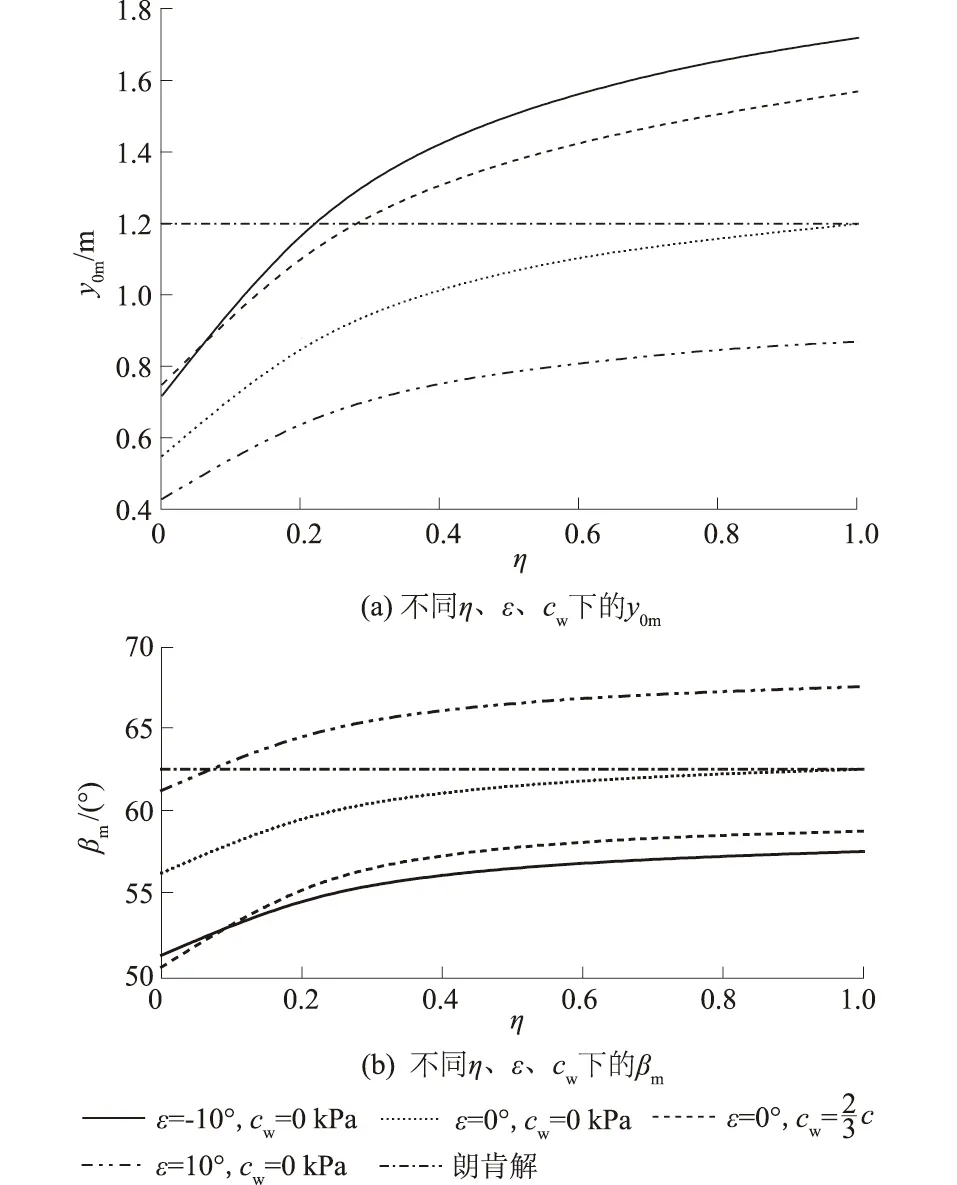
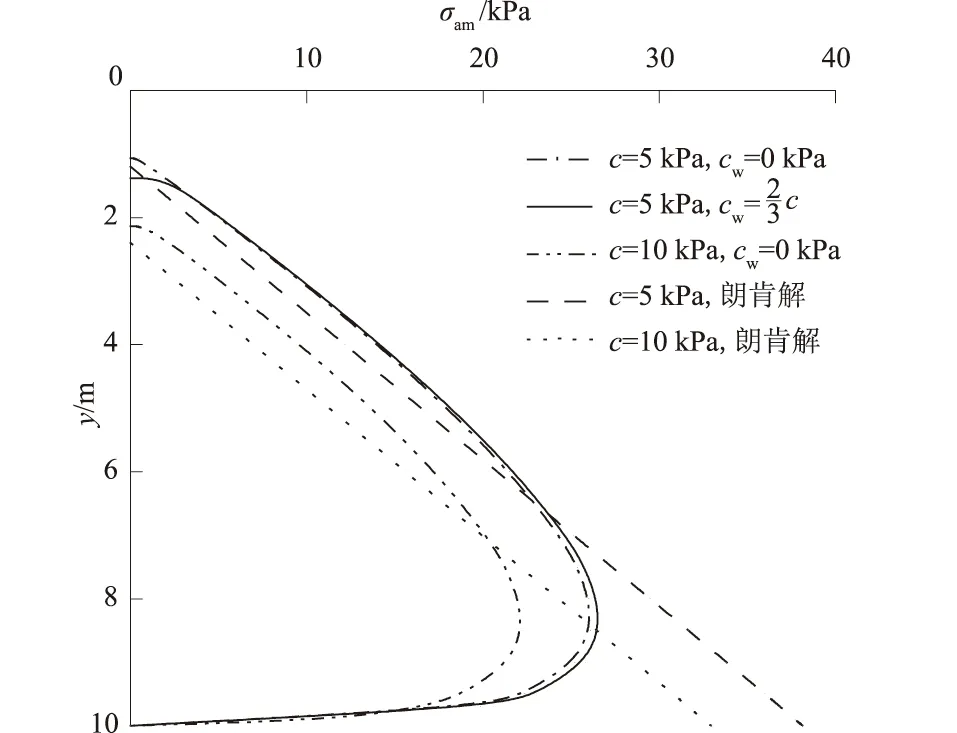
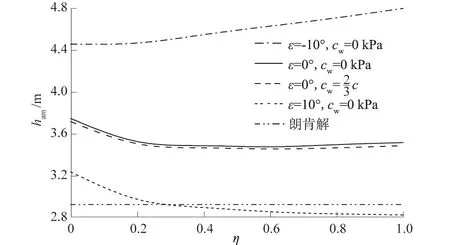
杨斌等[4]选取尺寸为1.8 m×0.3 m×1 m (长×宽×高)的试验箱进行试验。试验中以20号槽钢模拟挡墙,以保证其有足够刚度,并通过挡板上的螺杆控制其墙体位移,在墙背自上而下等间距埋设振弦式压力盒对不同工况下土压力进行测定,F2试验的材料为粉土。试验参数为:γ=19 kN/m3,φ=27°,δ=2φ/3,c=13.7 kPa,cw=2c/3,Sa=4 mm,q0=208.2 kPa,Rf=0.85,ε=0°,压力盒分别埋置在深度y=0.125、0.25、0.375、0.5、0.625、0.75 m处,试验中给出了不同位移下各压力盒的测土压力强度值的平均值,如表1所示,并给出了本文的理论值和朗肯解。需说明的是黏性填土产生裂缝的最大临界超载值q′=58.3 kPa,q′ 表1 不同位移下土压力理论解与试验值[4]对比Table 1 Comparison of earth pressure between theoretical solutions and experimental values[4] at different displacements 通过与两例模型试验进行对比分析,验证了本文理论公式。但仍然存在一定偏差,主要原因是参数取值误差以及模型试验并不是在半无限空间下开展的。 后文在进行参数分析时,如未特殊说明,均按下述取值:φ=35°,δ=2φ/3,δ0=φ/2,γ=16 kN/m3,c=5 kPa,cw=2c/3,Rf=0.85,ε=0°,η=0.5,q0=0 kPa。 图5为非极限状态下y0m及βm随φ、c、δ的变化曲线。可以看出,随着φ的增大,y0m及βm随之增大,主要是由于内摩擦角增大后,土体维持自身稳定的能力得到了加强。y0m随c的增大而增大,而βm与c无关,这是由于填土黏聚力增大了土颗粒间的凝聚力,但并不能改变破坏面与水平方向的夹角。随着δ的增加,y0m增加,而βm减小,并且y0m本文解不小于朗肯解,βm本文解不大于朗肯解,主要是由于墙背非光滑造成的。 图5 非极限状态下y0m及βm随φ、c、δ的变化曲线Fig.5 Variations of y0m and βm with φ,c,and δ under non-limit state 图6为非极限状态下y0m及βm随η、ε、cw的变化曲线。可以看出,随着η的增大,y0m、βm均增加,增长速率逐渐减小,主要原因是位移的增加使得内摩擦角得到了充分发挥,且内摩擦角随位移的增加也是先显著增加,而后趋于平缓。随着ε的增加,y0m减小,而βm增加,主要原因是墙背倾角增大,导致墙背对填土的支承作用加强造成的。随cw的增加,y0m增加,而βm减小,其原因是墙体与填土的黏着力增强使得土体更容易维持稳定而直立,则填土塑性区域更难滑动,即滑裂面倾角变缓。 图6 非极限状态下y0m及βm随η、ε、cw的变化曲线Fig.6 Variations of y0m and βm with η,ε,and cw under non-limit state 图7为不同η、ε下的非极限主动土压力变化曲线。随着η的增大,非极限主动土压力沿墙高同步减小,其原因是挡墙位移增大使得填土内部的能量耗散增多,则作用在墙体上的侧土压力就减小。随着ε的增加,分布曲线峰值下降,对于仰斜式挡墙,其底部受到的侧土压力较大,甚至出现凹向分布的可能。 图7 不同η、ε下的非极限主动土压力变化曲线Fig.7 Curves of non-limit active earth pressure with different values of η and ε 图8为不同c、cw下的非极限主动土压力变化曲线。随着c的增加,土压力分布高度及大小均减小,主要是由于填土黏聚力会抵消一部分土压力的缘故,并且参数相同时,墙体上部本文解要大于朗肯解,下部本文解要小于朗肯解,其主要原因是土拱效应导致了应力重分布,而cw对土压力分布影响甚微。 图8 不同c、cw下的非极限主动土压力变化曲线Fig.8 Curves of non-limit active earth pressure with different values of c and cw 图9为不同φ、δ下的非极限主动土压力变化曲线。非极限主动土压力随φ的增大而减小,主要是由于较大内摩擦角的填土只需要更小的外力便能够维持稳定。仅当δ=0°时,土压力才近似呈线性分布,说明墙背是否光滑是土压力呈非线性分布的关键原因。 图9 不同φ、δ下的非极限主动土压力变化曲线Fig.9 Curves of non-limit active earth pressure with different values of φ and δ 图10为不同η、ε、cw下的合力作用点深度变化曲线。随着η的增大,合力作用点深度先急剧减小,后趋于平缓,但对于仰斜式挡墙,会出现先减小,后增大的情况,这主要是由于张拉裂缝深度变化造成的。位移相同时,合力作用点深度随ε的增大而减小,cw对其影响甚微。仅对于墙背倾角较大的俯斜式挡墙在发生较大位移时,其合力作用点深度才有可能低于朗肯解。 图10 不同η、ε、cw下的合力作用点深度变化曲线Fig.10 Curves of the position of the resultant force acting point with different values of η,ε,and cw 图11为不同φ、c、δ下的合力作用点深度变化曲线。合力作用点深度随φ的增大而减小,当墙背较为粗糙时,则会出现先增大后略微减小的情况。合力作用点深度随δ的增大而上移,且明显高于朗肯解。合力作用点深度随c的增大而降低,这是由于c的增大导致了墙顶零应力区范围增大的缘故。 图11 不同φ、δ、c下的合力作用点深度变化曲线Fig.11 Curves of the position of the resultant force acting point with different values of φ,δ,and c (1)通过虚功原理,推导了一种可同时考虑位移、墙背倾斜且粗糙的黏性填土的张拉裂缝深度及滑裂面倾角的解析式,在此基础上,考虑了土拱效应,得到了倾斜挡墙黏性填土非极限主动土压力分布、合力大小、合力作用点深度的理论表达式。当满足朗肯假设时,朗肯裂缝深度、滑裂面倾角、合力值为其特解,将两例模型试验与公式解进行了对比,具有较好的一致性。 (2)裂缝深度与φm、cm、δm、cwm、η呈正相关,与ε呈负相关;潜在滑裂面倾角与cm无关,随ε、φm、η的增大而增大,而δm、cm对其影响则相反。 (3)墙背光滑时,土压力近似呈线性分布,合力作用点深度与朗肯解接近;墙背粗糙时,土压力则呈凸曲线分布,上部本文解大于朗肯解,下部反之,大小随η、φm、cm的增加而减小,峰值随ε的减小而有所提高,cwm对其影响甚微合力作用点深度仅在俯斜式挡墙发生较大位移时才可能低于朗肯解。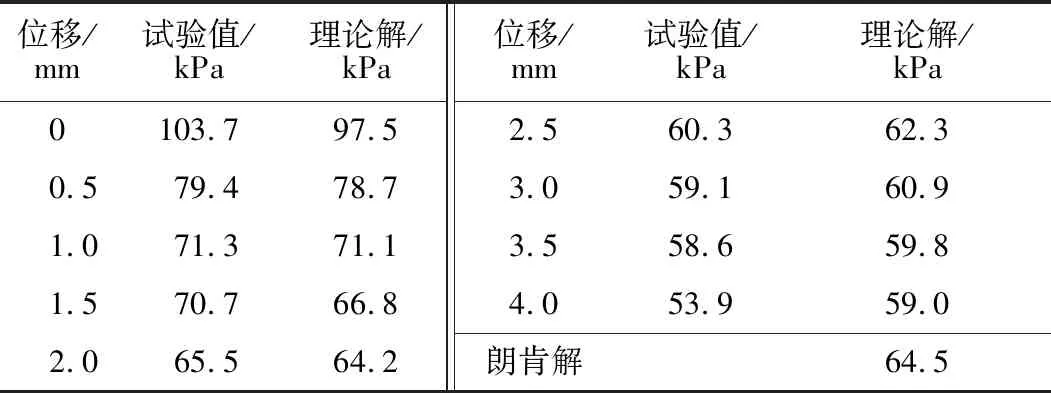
4 参数分析
4.1 张拉裂缝深度及滑裂面倾角

4.2 非极限主动土压力分布


4.3 合力作用点深度

5 结 论

