武汉九龙大桥桥塔拉索锚箱局部应力分析
魏顺波,潘 凡
[林同棪国际工程咨询(中国)有限公司武汉分公司,湖北 武汉 430020]
0 引言
采用有限元法对桥梁进行局部受力分析时,一般有3 种方法。第一种方法是对整个桥梁结构进行三维空间有限单元离散,可以求得全桥整体的变形和应力状态,但计算量非常巨大,一般的计算机很难满足要求。第二种方法是对第一种方法的改进,将局部结构处理为子结构,可使计算量减少许多,但仍然相当烦琐,不够灵活。第三种方法是依据圣维南原理进行局部分析,这时影响区外的计算结果与子结构计算结果较为接近,计算精度基本能满足工程要求。这是采用比较多的一种方法。
1 工程概况
九龙大桥为武汉市高新二路上的一座桥梁,跨越武汉外环线,全长519.08 m。桥轴线与外环高速公路斜交,斜交角49.4°。外环高速公路现状为双向四车道,路基宽度26.5 m。考虑斜交角及远期外环高速公路拓宽的可能性,主桥跨径采用(65+95)m。
主桥主梁采用钢箱梁,钢材材质Q 345qD,横断面为整体式闭合箱形断面,顶板宽36 m,底板宽26.6 m,梁高2.6 m。
主塔外观横立面呈斜伸的网球拍型,与竖直方向立面呈10°的倾斜角,塔高约66.1 m,桥面标高以上部分高约63.5 m。主塔采用钢箱截面,截面尺寸为3.6 m×3.6 m,拱肋采用Q 345qD 钢材。
主桥为双索面斜拉桥,斜拉索在梁上锚固于箱梁两侧距桥梁中心线13.75 m 处。全桥共20 对斜拉索。斜拉索在65 m 跨侧梁上的顺桥向间距为3.5 m,在95 m 跨侧梁上的顺桥向间距为5 m。
2 拉索与桥塔锚箱局部应力分析
2.1 分析模型
选取锚箱M 10 进行建模分析,如图1 所示。
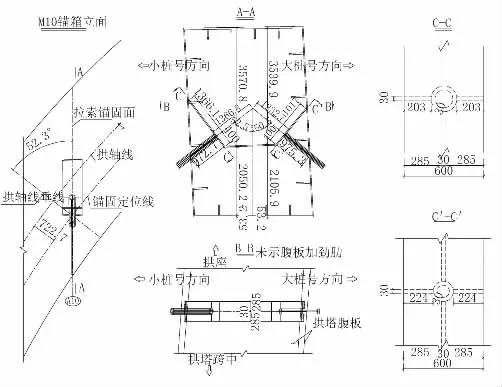
图1 锚箱M10 构造图(单位:mm)
运用有限元软件建立三维模型,如图2 所示。模型全部采用壳单元模拟,共12 668 个单元,12 826 个节点。模型边界条件为约束上下端头的拱肋。模型荷载在采用整体分析得到的极限组合下,锚箱M 10 对应的拉索的索力进行加载。模型网格划分如图3 所示。
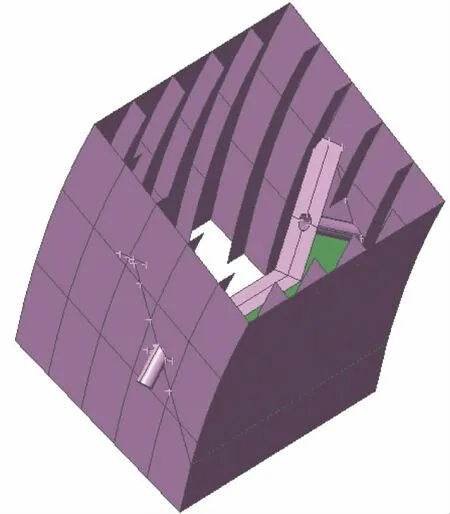
图2 锚箱有限元模型

图3 有限元模型网格划分示意
2.2 材料参数
材料均采用Q 345 钢材,弹性模量E=2.06×105MPa,泊松比ν=0.3,质量密度p=7.698×103kg/m3,线膨胀系数α=1.2×10-5。其中钢板厚度最大为30 mm,最小为24 mm。
2.3 强度分析结果
以下为最大、最小索力工况下M 10 锚箱的有限元分析结果,对于最小索力工况下仅给出Mises 应力图和剪应力图。M 10 锚箱有限元分析结果如图4~图7 及表1 所示。
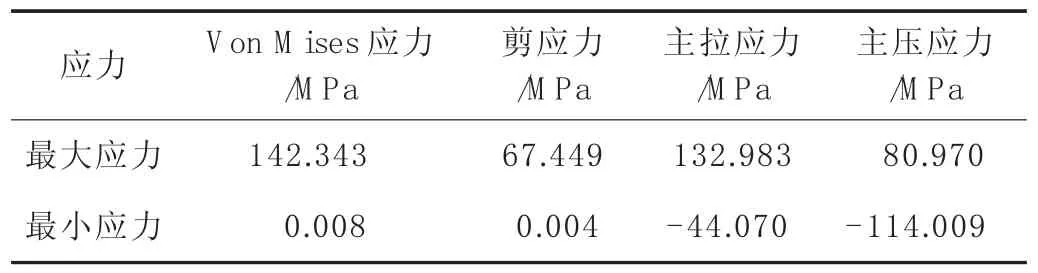
表1 最大索力工况下锚箱应力

图4 最大索力工况Von Mises 应力云图(单位:kPa)
2.3.1 最大索力工况
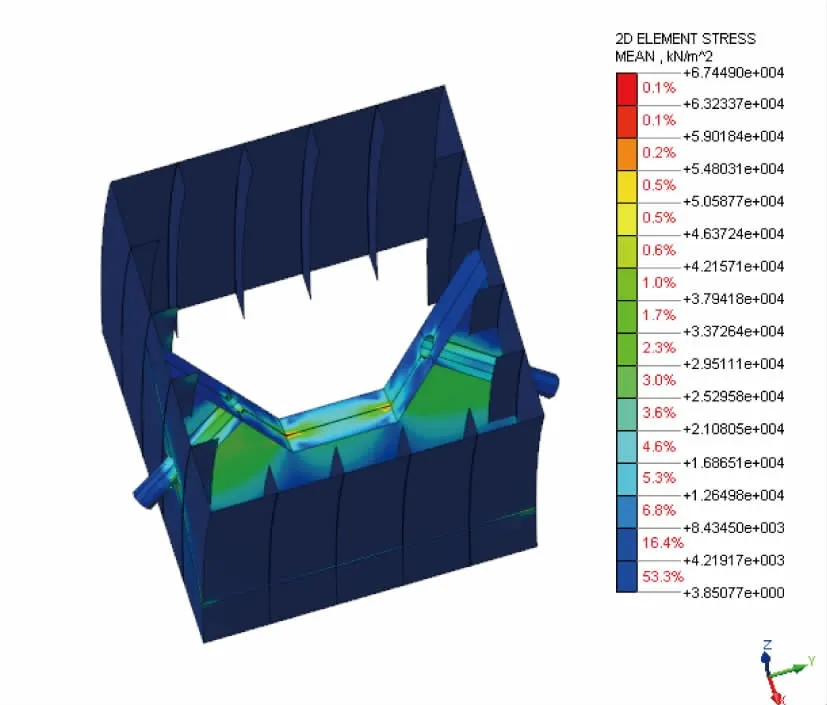
图5 最大索力工况最大剪应力云图(单位:kPa)
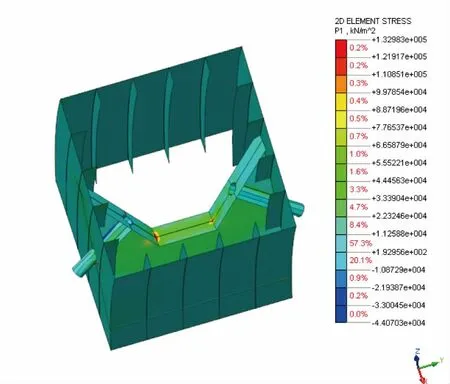
图6 最大索力工况主拉应力云图(单位:kPa)
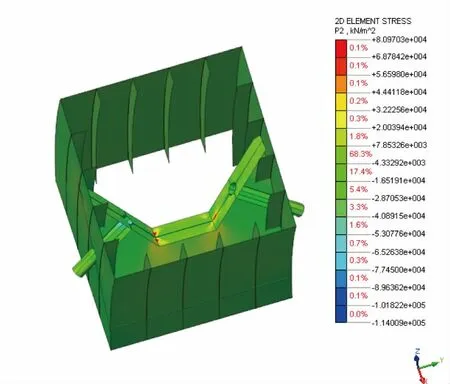
图7 最大索力工况主压应力云图(单位:kPa)
最大索力工况下,钢锚箱最大Von Mises 应力为142.34 MPa,最大剪应力67.45 MPa,最大主拉应力132.99 MPa,最大主压应力-114.01 MPa 满足强度要求。最大应力出现在承压板与隔板连接处、隔板与拱肋连接的角隅处。这些地方出现了明显的应力集中。索塔锚固区各板件钢材在复杂的应力状态下工作。钢材的屈服并不只取决于某一方向的应力,可由反映各方向应力综合影响的强度理论来确定。对于材质均匀各向同性的钢材,通常采用二、四强度理论来确定相应的破坏准则。经常采用Von Mises 应力来判断材料的屈服条件。该判别准则如下:
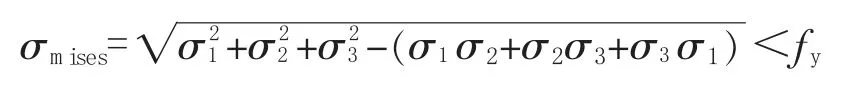
式中:σmises为Von Mises 应力,σ1、σ2、σ3为3 个方向主应力,fy为材料屈服强度。
依据《钢结构设计规范》(G B 50017—2017)、《公路钢结构桥梁设计规范》(JTG D 64—2015),Q 345qD钢屈服强度345 MPa,轴向抗拉压强度取200 MPa。因此,锚箱各板件的承载能力符合要求。
进一步将锚箱隔板分离出来查看其应力水平。由图8 锚箱隔板的Von Mises应力水平多在40~50 MPa左右,应力水平较低。应力通过隔板传向拱肋。索导管与隔板连接处应力水平较高。由图9 可见,锚箱隔板的最大剪应力多在40 MPa 以下。由图10 可见,锚箱隔板最大主拉应力多在50 MPa 以下。由图11 可见,锚箱隔板最大主压应力多在-50 MPa 以下。

图8 最大索力工况隔板最大Von Mises 应力云图(单位:kPa)
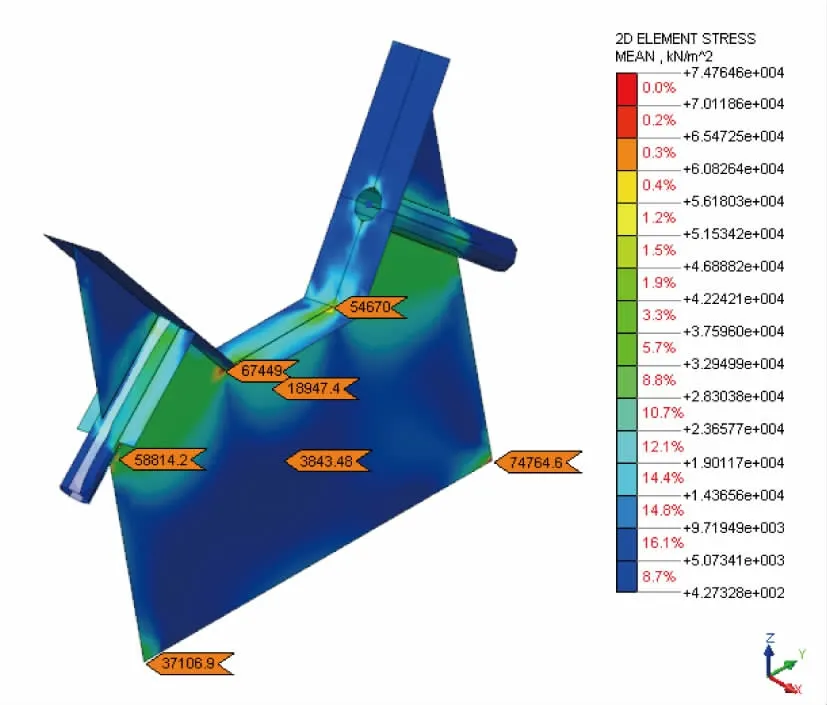
图9 最大索力工况隔板最大剪应力云图(单位:kPa)

图10 最大索力工况隔板主拉应力云图(单位:kPa)
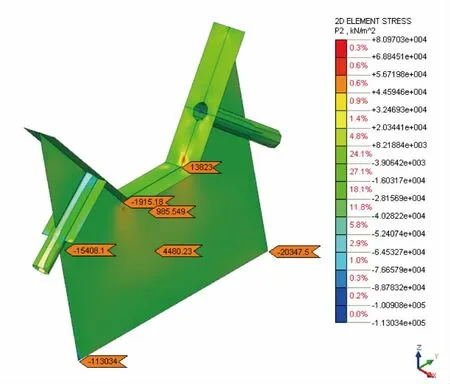
图11 最大索力工况隔板主压应力云图(单位:kPa)
由以上分析可知,最大索力作用下,锚箱整体应力水平满足强度要求,但是对于锚箱、索导管、拱肋、隔板连接处应力集中较为明显。设计时对于这些部位应进行细致的处理,避免应力集中。对于关键部位疲劳细节,应从施工制造工艺等方面加强要求,避免应力过分集中,以防出现疲劳裂纹发源处。
2.3.2 最小索力工况
由图12、图13 可见,最小索力工况下钢锚箱最大Von Mises 应力为68.74 MPa,最大剪应力33.20 MPa满足强度要求。同样,一些角隅处出现了明显的应力集中。
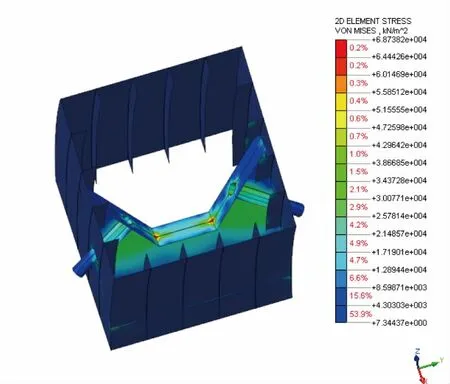
图12 最小索力工况Von Mises 应力云图(单位:kPa)
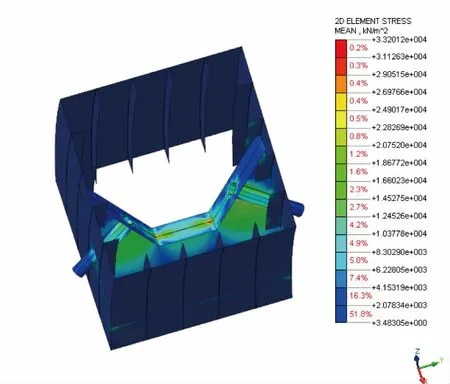
图13 最小索力工况最大剪应力云图(单位:kPa)
2.3.3 隔板最大应力工况下特征值屈曲分析结果
为了进一步了解最大索力作用下,锚箱隔板的受压稳定性特性,在以上模型的基础上进行了锚箱线性屈曲分析。取出1 阶屈曲模态如图14 所示。
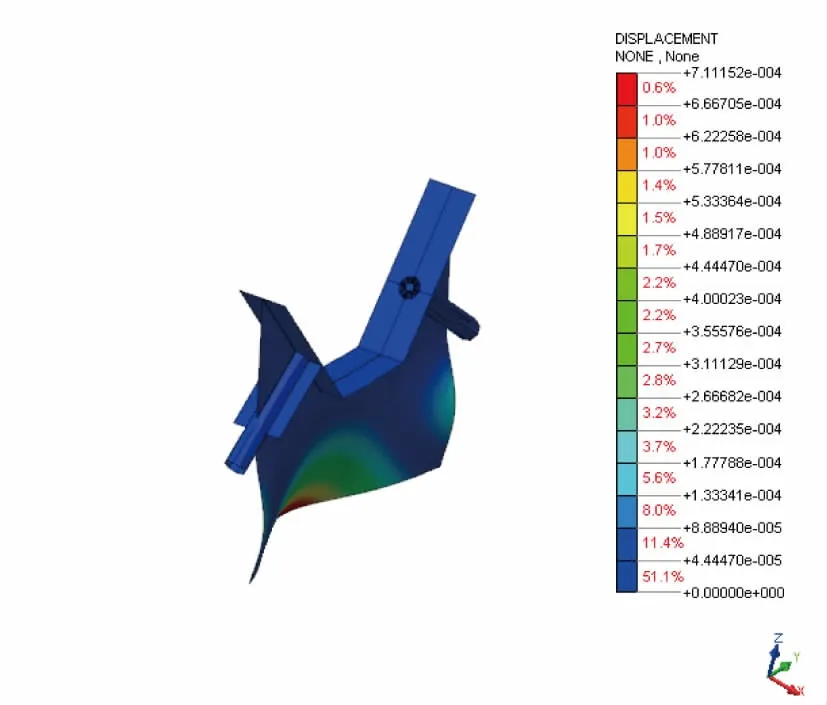
图14 1 阶屈曲模态
锚箱最大索力作用下屈曲模态对应的荷载因子见表2。分析可知,在最大索力作用下,锚箱的下隔板最容易首先出现屈曲破坏。其屈曲破坏时的荷载因子为13.735 倍最大索力。以上分析未考虑初始缺陷、材料非线性等的影响,仅供参考,设计时可根据相关规范对该隔板设置加劲。

表2 各屈曲模态对应的荷载因子
3 计算结果
最大索力工况下,钢锚箱最大Von Mises 应力为142.34 MPa,最大剪应力为67.45 MPa,最大主拉应力为132.99 MPa,最大主压应力为-114.01 MPa,满足强度要求。
锚箱、索导管、拱肋、隔板连接处应力集中较为明显,设计时对这些部位应进行细致的处理,避免应力集中,成为疲劳裂纹源。
最大索力作用下,锚箱的下承压隔板最容易首先出现屈曲破坏。其屈曲破坏时的荷载因子为13.735 倍最大索力,可对该隔板适当加劲。
4 结语
锚箱为传力的关键环节。本文结合工程实例,对拉索与桥塔锚箱局部应力分析进行探讨,首先建立整桥模型进行整体分析,再将整体分析的各工况的索力作为荷载施加到结构上进行局部分析,从而了解锚箱结构的局部受力特征。对于该钢锚箱结构,主要从强度、隔板的稳定性等方面进行检算。

