基于CFD的火箭滑橇水刹车水动性能分析
李新颖,肖 军,张家旭,胡 奇,孙 丰
(1.中国特种飞行器研究所,湖北荆门 448035;2.高速水动力航空科技重点实验室,湖北荆门 448035;3.中国华阴兵器试验中心,陕西华阴 714200)
火箭滑橇是以火箭发动机作为动力并沿专用的高精度直轨道运行的装置,用以进行气动力、材料、引信、制导与控制系统的冲击和破坏实验[1]。在火箭滑橇运动的终点段,往往需要对橇车进行制动和刹车以实现被试品与火箭滑橇分离或软回收,为了减小制动时的阻力、过载和加速度,多采用水刹车方式[2]。水刹车的原理是当高速滑行的火箭滑橇进入制动段后,水刹车装置将水槽里的水戽起,水流在水刹车内部旋转一个角度后喷射出来,这样橇车的动量转换成了水的动量,从而获得强大的制动力,达到快速刹车的目的[3]。由于水刹车具有经济、灵活、制动能力大等特点,因此被广泛应用于火箭滑橇试验[4]。
火箭滑橇水刹车一般是在高速、大过载下运行的,各个装置承受很大的作用力,工况极其恶劣,所以在设计过程中需要进行受力分析[5],然而物理试验往往面临成本高、周期长等问题。 随着计算流体力学(Computational Fluid Dynamics,简称CFD)和高性能计算机的发展和应用,CFD 技术在航空、航天、船舶和兵器等领域的水动性能预报方面发挥着越来越重要的作用,渐渐变成与物理试验并驾齐驱的研究手段。CFD具有成本低、周期短、无缩尺比效应等优点,且能以较少的人力、物力和时间为物理试验提供指导[6-7]。
本文针对火箭滑橇水刹车超高速(1Ma)戽水过程中的强非线性内外流耦合的气水两相流问题,提出了一种基于雷诺应力模型结合VOF方法的水动性能数值计算方法,研究了水刹车在不同航速、不同吃水下的水动性能。
1 几何模型及研究工况
以某双轨火箭滑橇三角形水刹车为研究对象,在数值计算时,对模型进行了简化处理,见图1。

图1 水刹车模型Fig.1 The water brake model
水刹车在制动段运动时,受戽斗入水口高度的限制,在速度不断减小的情况下,制动力会越来越小,因此,为了保证一定的制动力,水刹车的吃水应逐渐增大,吃水基准线为水刹车最低点处,见图2。数值计算时,取水刹车管道内壁5 个截面共38 个点进行压力监测,见图3,最终得到水刹车在不同航速、不同吃水下的水动阻力和局部压力,研究工况见表1。

图2 吃水基准线Fig.2 Draft baseline

图3 压力监测点(半模)Fig.3 Pressure monitoring point (half model)

表1 研究工况Tab.1 Study cases
2 数值方法
2.1 控制方程
任何CFD 均是基于流体力学基本控制方程:连续方程、动量方程与能量方程[8]。针对水刹车水面超高速戽水过程中的气水两相流问题,若只对水动性能进行计算,则可考虑流动为等温条件下的不可压缩流动,即不考虑空气和水的压缩性,只考虑重力,故最终的方程形式如下所示。
连续方程:
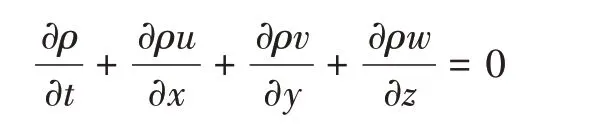
动量方程:

上式中,ρ为密度,t为时间,u、v、w分别为x、y、z方向上的速度分量,p为静压,μ为动力黏性系数,g为重力加速度。
为了精确模拟湍流运动、管道内流场和自由液面外流场,采用比常规两方程模型(如k-ε和k-ω)精度更高的雷诺应力模型(Reynolds Stress Model(RSM,7方程))结合壁面函数法来模拟,离散方法采用有限体积法,空间离散格式采用二阶迎风格式,时间离散采用隐式方法,离散方程的求解选用Coupled 方法,自由液面捕捉采用VOF方法。
2.2 雷诺应力模型
粘涡模型中雷诺应力采取了各种假设而达到了简化,许多湍流流动的细节会被忽略,故不能很好地预测复杂流动。与粘涡模型不同的是,雷诺应力模型不采用Boussinesq 假设,而是直接对时均N-S 方程中的二阶脉动相关项提出其相应的偏微分方程组,由于在方程组中还出现了湍流动能k及耗散率ε,故增加了相应的k与ε 方程,在求解时,需要额外求解6 个雷诺应力方程、k方程与ε方程。增加的雷诺应力微分方程考虑了更多的湍流细节,所以雷诺应力模型能更真实地模拟实际的湍流流动,反映其内在本质,这一模型的优点在于可准确地考虑各向异性效应[9-10]。
2.3 VOF方法
VOF方法根据各个时刻流体在网格单元中所占体积函数F来构造和追踪自由液面,若在某时刻网格单元中F=1,则说明该单元全部为指定相流体所占据,为流体单元;若F=0,则该单元全部为另一相流体所占据,相对于前相流体则称为空单元。当0<F<1时,则该单元为包含两相物质的交界面单元[11]。F函数的控制方程可以写成下列形式,即

由于VOF 方法追踪的是网格中的流体体积,而不是流体质点的运动,因而具有容易实现、计算量小和精度高等优点,并且可以处理自由液面大变形和拓扑结构发生变化等复杂三维情况[12]。
3 数值计算及分析
3.1 网格划分
网格划分时,采用非结构六面体的网格布局形式,取半模进行网格划分和计算,计算域大小如下(L为模型纵向长度):
(1)模型首部离前边界(Inlet):1L;
(2)模型尾部离后边界(Outlet):5L;
(3)自由液面离上边界(Top):2L;
(4)自由液面离下边界(Bottom):2L;
(5)模型对称面离侧边界(Side):2L。
沿航向模型表面布置约480 个网格,自由液面处的网格大小为X=Y=50Z=50×L/1000,模型首部、管道内部和流场变化剧烈区域的网格适当进行细化,添加边界层网格,Y取40,最终网格量为2500 万~3200 万。网格示意图见图4-5。

图4 全局网格(航速340m/s,吃水40mm)Fig.4 Global mesh (speed = 340m/s、draft = 40mm)

图5 模型网格(航速340m/s,吃水40mm)Fig.5 Model mesh (speed = 340m/s、draft = 40mm)
3.2 结果分析
数值计算时,模型壁面为无滑移边界,即考虑黏性,最大非线性迭代次数为20,时间步长取ΔT=0.001L/V(V为航速)。
表2 为水动阻力计算结果与试验结果,其中试验结果依据试验时的橇车质量和最大纵向加速度获得。表3 为监测点的压力值。图6-图10 为不同工况下的流场示意图。
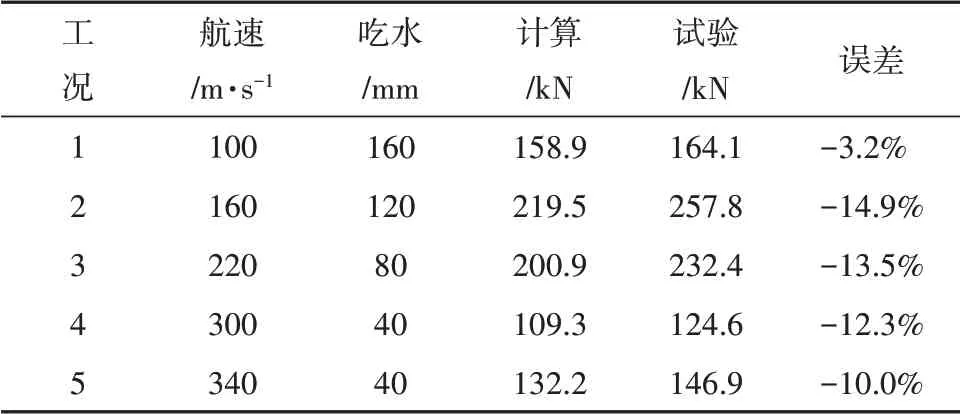
表2 水动阻力结果Tab.2 Hydrodynamic resistance results

图6 流场示意图(航速100m/s,吃水160mm)Fig.6 Figure of flow field (speed = 100m/s, draft = 160mm)
由表2 可以得出,水动阻力的数值计算精度达到85%;航速为160m/s、吃水为120 mm 时,水动阻力达到最大。由表3 可以得出,在水刹车水流入口处,由于与水存在撞击,入口处的局部压力较大;水刹车管道转弯处和出口处,由于管道的离心作用和水流的冲击作用,局部压力较大。由图6-图10可以看出,水刹车在航行过程中,外部水流会沿水刹车外侧面和下表面进行爬升直至流向尾部,内部水流会通过戽斗并经管道旋转后向两侧喷出。

图10 流场示意图(航速340m/s,吃水40mm)Fig.10 Figure of flow field (speed = 340m/s, draft=40mm)
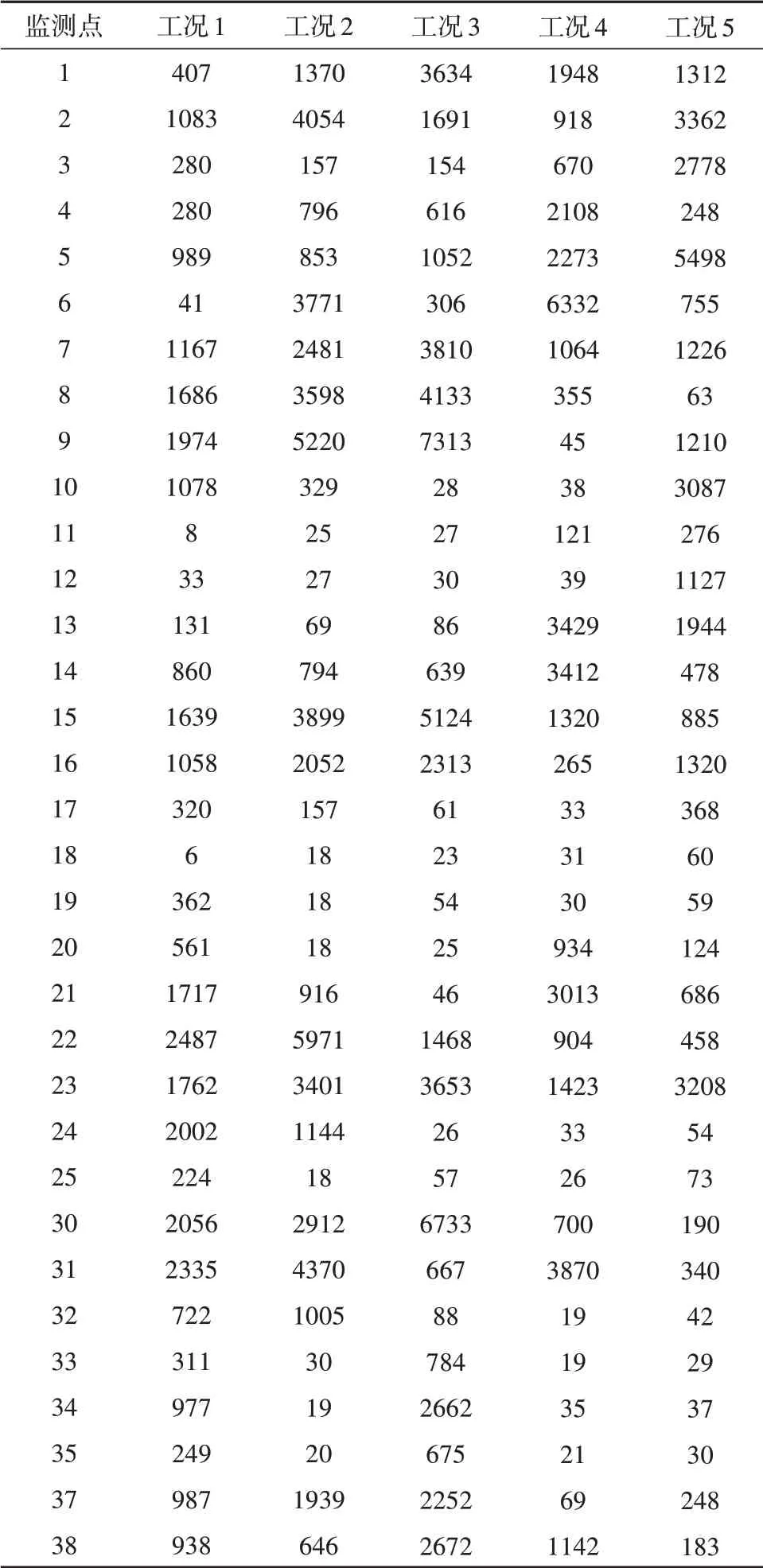
表3 监测点压力值(KPa)Tab.3 Monitoring point pressure(KPa)
4 结论
采用雷诺应力模型结合VOF 方法对水刹车水面超高速戽水过程的水动性能进行了数值分析,计算精度达到85%,验证了方法的可行性,为水刹车外形设计和强度校核提供技术支持;水刹车在航行过程中,外部水流会沿水刹车外侧面和下表面进行爬升直至流向尾部,内部水流会通过戽斗并经管道旋转后向两侧喷出;水刹车航速为160 m/s、吃水为120 mm 时的水动阻力最大,另外水刹车入口处、管道转弯处和出口处的局部压力较大,结构设计时应适当加强。

图7 流场示意图(航速160m/s,吃水120mm)Fig.7 Figure of flow field (speed = 160m/s, draft = 120mm)

图8 流场示意图(航速220m/s,吃水80mm)Fig.8 Figure of flow field (speed = 220m/s, draft = 80mm)

图9 流场示意图(航速300m/s,吃水40mm)Fig.9 Figure of flow field (speed = 300m/s, draft = 40mm)

