基于LSTM神经网络的LNG储量预测

余 杨，彭湘媛

（同济大学控制科学与工程系，上海 200092）

液化天然气（LNG）为当今世界发展最快的燃料之一。据预测，世界上的LNG 需求到2030年会比之前高出两倍［1-2］。近十几年来，我国LNG 消费的需求量飞速上升［3］，尤其是在东部地区和东南沿海等经济较为发达的区域，LNG在能源消费总值中的占比不断提升。根据中国可持续发展油气资源战略研究报告的预测，未来15年，我国LNG 需求量将出现指数增长，年均增速达10.8%，而LNG 生产量增长的速度却远低于需求增长速度，年增长率仅为7.5%，依赖进口的程度会越来越大［4］。

同时，LNG能源具有一定的不确定性，这也使整个产业面临着一定的挑战。要在市场中站稳脚跟，实现利益最大化，需要提前严格把控每月的LNG 储量，在不造成积压的前提下尽量满足市场需求。LNG销售公司需要综合考虑各种影响因素，对公司LNG 储量做出相应预测，提高经济效益，避免LNG 库存储量不够、满足不了市场需求，或是储量过剩但销售渠道不足［5］。

针对LNG 储量预测问题，本文首先阐述了针对实际天然气储量及影响因素的一些预处理方法，对影响因素的相关性进行了分析，运用互信息理论对影响因素进行筛选。然后利用LSTM 长短期记忆（Long Short Term Memory）神经网络［6］对LNG储量进行了预测并对模型进行优化，检验了预测结果的准确度和变化趋势，最后与传统预测方法——灰度预测［7］对比，验证LSTM模型的正确性和可行性。

1 基于互信息的相关因素分析

根据实际调研，影响LNG 储量的因素有LNG 储罐大小、运营水平、市场价格、美元兑人民币汇率、通航能力、码头能力和天气等。这些因素对LNG 储量的影响不尽相同。本文基于互信息的方法对这些因素进行相关性分析［8-10］。

1.1 基于互信息的相关性分析

信息熵（Entropy）是信息的基本单位，用于描述离散变量是分散还是聚合。信息熵越大，代表变量的分布越离散，描述该变量需要的信息越多。离散型随机变量X的信息熵定义如式（1）所示，即

其中，p（x）表示每种可能的取值x的概率，底数b可取不同的值，表示信息熵有不同的量纲。

互信息表示两个或多个变量之间共享的信息量。互信息越大，变量之间的相关性越高。本文均为离散变量，对于两个随机离散变量X，Y之间的互信息定义如式（2）所示，即

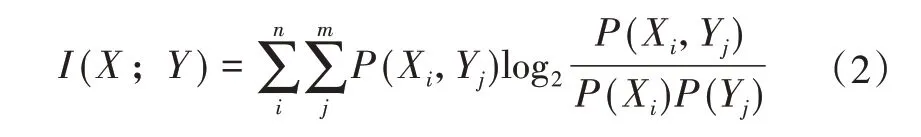
其中，Xi代表变量X中的第i个值；Yj代表变量Y中的第j个值；P(Xi，Yj)表示变量X为第i个值与变量Y为第j个值时的联合概率密度，P(X) 和P(Y) 为独立密度。I(X；Y)越大，变量X包含关于Y的信息就越多。因此可用互信息来度量变量间的相关性。

通过式（2）计算LNG 储量各影响因素与因变量的互信息，将互信息超过一定阈值（T1）的变量筛选出来，作为冗余过滤器的输入集合。经过计算，各变量与LNG储量的相关度见表1。

表1 LNG影响因素相关度排名Tab.1 The rank of the correlation degree of LNG influencing facton

计算出各影响因素的相关性后，经过反复实验，将相关性过滤器的阈值T1定位为0.050000，即相关性小于0.050000的影响因素被滤除，不再进入冗余过滤器。因此，气温（℃）这一影响因素因为相关度仅为0.002439而被滤除。

1.2 基于互信息的冗余过滤器

一个特征值关于目标变量的信息内容可以被其他特征值表示出来时，这个特征值称为冗余特征值。冗余特征不仅会恶化预测性能，而且还会影响算法学习的速度。因此，用于预测数据必须去除冗余特征值。本文提出了一种基于互信息的冗余性分析方法。算法的具体步骤如下：

（1）所有候选特征值进行线性归一化处理，范围为［0，1］。归一化的具体表达式如式（3）所示，即

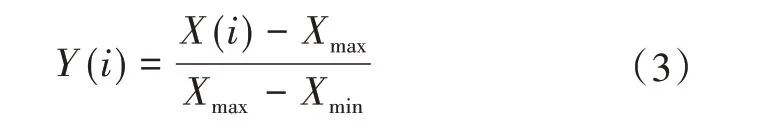
其中，Xmax，Xmin分别代表变量X中的最大值和最小值，Y为归一化后的结果。

（2）计算待选输入与目标变量相关性。第i个待选输入Xi对于目标变量Y的相关性记为D(Xi)，计算公式如式（2）。

（3）筛选出相关度超过预先设定的阈值T1的m个特征值，并放入相关性选择特征集SRelevance中，用作冗余性分析。

（4）将SRelevance中相关性排名第一的特征值添加到SFinal中，将冗余过滤计数器的i变为2。

（5）SRelevance中被选中的第i个特征值的冗余度记为R(i)，计算公式如（4）所示，即

其中，Xs代表已经通过冗余过滤器而得到的特征量，R（i）表示Xi与SFinal中特征量的最大冗余值。

（6）如果R（i）大于提前设定的阈值T2，特征值Xi冗余，将其滤除。否则Xi添加到SFinal，冗余过滤器的计数器加1。

（7）如果i达到m+1，结束特征值选择。SFinal即为选择后的结果，准备输入给LSTM 神经网络进行预测训练。

经过冗余滤波器筛选，可以看到这五个变量中通航能力的冗余性较大，即含有较多的重复信息。另一方面，因包含的信息越多，神经网络训练所得的结果就越准确，因此也不能将变量减少过多。经过反复实验，将冗余过滤器的阈值T2设定为0.80000。冗余度大于T2的变量，即通航能力将被滤除，无需进入后续LSTM神经网络预测。

2 LSTM 神经网络预测模型

为了解决时序数列预测的需求问题，循环神经网络RNN 被提出，其独特的网络结构为处理上下文存在关联性的内容提供了极大的方便，解决了BP神经网络等传统神经网络存在的效率不高、准确性较低等问题。传统的RNN 神经网络会在层与层之间传递信息时出现爆炸或梯度消失的情况，并且每次都会采用独立的数据向量，没有内存帮助其处理需要记忆的任务，因此LSTM长短期记忆预测模型被提出。

依据相关性信息的筛选，本文使用了5 类输入特征，包括运营水平（车）、市场价格（元/吨）、美元兑人民币汇率、码头能力（船）以及LNG 历史储量（万吨），通过不同输入数据筛选出对LNG 储量预测较为合适的特征进行分析。

2.1 输入数据处理

（1）异常值处理。

在构造数据集过程中难免会遇到异常值问题，由于相关性特征构造时需要对所有的数据进行简化操作，最终主要的时间序列以筛选后的数据为准，其他相关的多余数据只能做删除处理；同时当码头因突发情况无法运行时，需要对其进行异常值填充处理，对于因政治原因无法通行的情况直接将其填充为0。

（2）数据归一化处理。

由于影响因素间各个数据存在量级上的差距，有的特征如市场价格达到了千以上的数量级，而有的特征如码头能力、通航能力只有1-10 数量级，在神经网络学习时会偏向于将数值较大的特征认为是主要特征而忽略了细小的特征，然而对LNG 销售产业而言，码头能力的关注度却经常大于市场价格。为了不对预测结果造成偏差，需要对各个特征进行归一化处理，将数值缩放到［0，1］区间，同时也是为了便于神经网络进行学习，归一化方程如式（5）所示，即

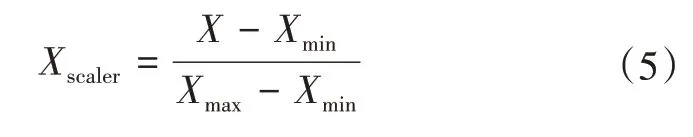
2.2 模型结构设计

LSTM 网络模型结构主要是“输入层-隐藏层-输出层”，模型的隐藏层搭建通常运用Keras 学习框架中的Dense 层、PReLU 层、LSTM 层和Dropout 层。在输出层方面，LNG 储量回归预测利用Dense 层对预测结果进行回归，输出值即为预测值。输入层的神经元个数由输入参数所决定，输出层结构根据预测类型不同进行区分，因为隐藏层结构目前还没有具体的理论指导，因此尝试使用Dense层与LSTM 层结合进行多种模式探索。本文所用模型的网络结构如图1 所示，其中隐藏层的层数需要经过测试才能最终得出。

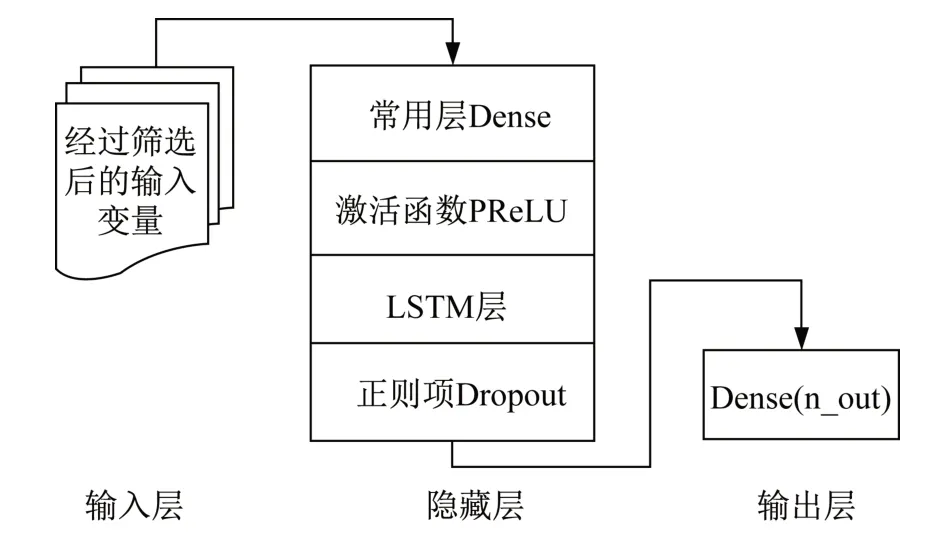
图1 LSTM 模型结构Fig.1 The structure of LSTM

网络模型可以分为以Dense 为主的结构、以LSTM为主的结构以及两者混合结构。隐含层中根据需要添加Dropout层防止过拟合。加入Dropout就是为了随机删减某些数据，让模型有更多种尝试的可能性，从而提高模型的泛化能力。其中选择PReLU 作为激活函数。神经元个数关乎到模型学习速度的快慢，但是过多和过少都对训练没有帮助，因此将使用试凑法进行测试。

2.3 模型初步预测结果

模型初始时使用常用损失函数MSE（Mean Squared Error，均方误差），优化器为SGD，批量数初始值设置为10，训练次数为2000 次。仿真结果如图2 所示。图2（a）表明，预测结果与实际值仍有一定的误差，尤其是在起伏较大的位置，预测值与实际值偏离较为严重。此外，预测趋势应该保持基本正确，即后一个月预测值较前一个月的储量是增加还是减少，应与实际情况保持一致。这样可以增加企业运营的稳定性，使其更有能力对未来市场进行把控。如果趋势出现了较大偏差，同样会引起较大利益损失。因此，本文对趋势的变化进行了作图检验（用后一个月储量数值减去前一个月储量数值），结果如图2（b）所示。由图2（b）可以看出，预测趋势与实际变化趋势存在严重的不一致。

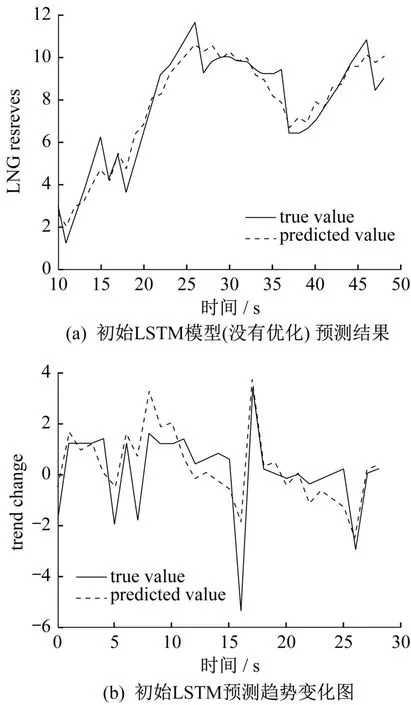
图2 初始LSTM模型（没有优化）的预测结果Fig.2 The prediction of LNG reserves by initial LSTM model

3 LSTM预测模型的优化

如前文所述，LSTM 模型对于预测结果并不达标，因此本文又在多个方面对其进行了优化，使得最终的相对误差绝大多数控制在5% 以内，即使存在个别异常值，也不超过10%。

3.1 修改Batch Size

Batch Size 为一次训练所选取的样本数。在没有使用Batch Size 之前，意味着网络在训练时，是一次性地把所有的数据（整个数据库）输入网络中，然后计算其梯度进行反向传播，由于在计算梯度时使用了整个数据库，所以计算得到的梯度方向更为准确。但在这种情况下，计算得到不同梯度值差别巨大，难以使用一个全局的学习率。在样本数很小的数据库中，没有Batch Size 是可以接受的，而且效果也很好。但是一旦是稍大些的数据库，一次性地把所有数据输入网络，肯定会引起内存的爆炸，所以这时就需要一个Batch Size。

Batch Size 的数值关乎模型的优化效率和速度，同时直接影响到GPU 内存的使用情况，假如GPU 内存不大或是数据集较小，该数值最好相应设置得小一些。设置合适的Batch Size会使梯度准确，预测效率和准确率同时也得到提高。Batch Size 的优化结果如表2所示。

由表2 可见，改变训练样本数，预测效果会发生较为明显的改变，从原定的Batch Size 为10 开始逐渐减小，预测曲线更加贴近真实值，相对误差减小，准确度提升。当Batch Size 为4 时，模型达到饱和状态，之后继续减小训练样本数，误差将会再次增大。因此将Batch Size的最终值定为4。

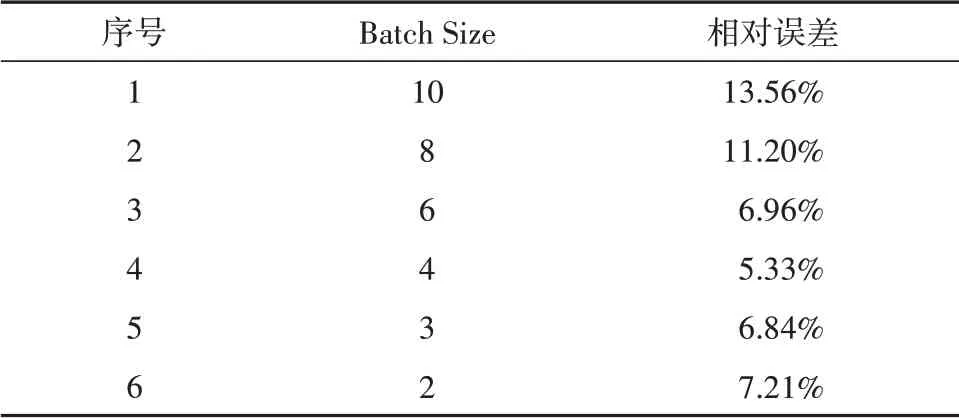
表2 Batch size 优化预测结果统计表Tab.2 The statistics of Batch size optimization effect

3.2 修改损失函数

通过损失函数可以看到模型的优劣，为研究提供了优化的方向，但是每个模型的损失函数并不是通用的［11］。损失函数的选取依赖于参数的数量、异常值、机器学习算法、梯度下降的效率、导数求取的难易和预测的置信度等若干方面。原损失函数为均方误差MSE，它是预测值与目标值之间差值的平方和，公式如式（6）所示，即

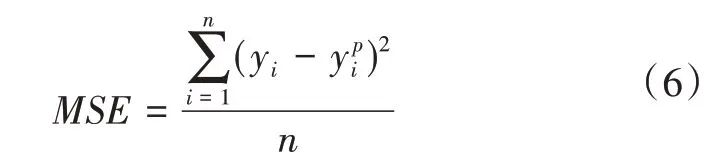
这一步优化中将损失函数由MSE变换为平均绝对误差（Mean Absolute Error）。MAE是另一种常用的回归损失函数，它是目标值与预测值之差绝对值的和，表示预测值的平均误差幅度，而不需要考虑误差的方向，范围是0到无穷，计算公式如式（7）所示，即

一般情况下，利用均方误差更容易求解，但平均绝对误差则对于异常值更稳健。由于均方误差（MSE）在浮动较大的位置损失通常高于平均绝对误差（MAE），它会给这样的值赋予更大的权重，而模型会试图减小异常值造成的误差，导致模型整体表现下降。所以当训练数据中含有较多的异常值或起伏较大时，平均绝对误差（MAE）更为适合。当对所有观测值进行处理时，如果利用MSE进行优化会得到所有观测的均值，而使用MAE则能得到所有观测的中值。与均值相比，中值对于异常值的鲁棒性更好，这就意味着平均绝对误差对于异常值有着比均方误差更好的鲁棒性。MSE和MAE的预测结果如表3所示。

表3 损失函数优化结果统计表Tab.3 The statistics of loss function optimization effect

由表3 可以看出，将损失函数由MSE 调整为MAE后，由于原始数据本身起伏较大，更适用于平均绝对误差，预测效果得到较大程度改善。但与目标值5% 的误差仍然有一定距离，因此还需要继续优化。

3.3 修改优化器

其实机器学习训练过程的本质就是使损失最小化，故定义损失函数后，优化器会在其中发挥重要作用。在深度学习中，通常对于梯度进行优化，优化的目标就是优化网络模型里的参数θ（θ是一个集合，θ1、θ2、θ3，…）。本文将原优化器SGD 修改为RMSProp。理由是SGD 在随机选择梯度的同时会引入噪声，使得权值更新的方向不一定正确，即更新比较频繁，会造成损失函数有严重的震荡。此外，SGD 也不能单独克服局部最优解的问题。

相比之下，RMSProp算法给每一个权值一个变量，MeanSquare（w，t）用来记录第t次更新步长时前t-1 次的梯度平方的平均值。然后再用第t次的梯度除以前t-1 次的梯度平方的平均值，得到学习步长的更新比例。迭代更新公式如式（8-9）［13］，即

通过RMSprop，可以调整不同维度上的步长，加快收敛速度。根据比例会得到新的学习步长。如果当前得到的梯度为负，学习步长就会减小一点；如果当前得到的梯度为正，学习步长就会增大一点。 因此RMSProp算法步长的更新更加缓和。优化器修改前后的预测结果如表4所示。

表4 优化器优化结果统计表Tab.4 The statistics of optimizer optimization

由表4 可知，将优化器改为RMSProp 后，预测结果达到了小于5%的目标，实现了相对可靠的预测。

3.4 综合优化

最后将三种优化方式同时作用于LSTM 模型，得到的最终预测效果如图3所示。

由图3 可知，经过优化后预测效果得到较大改善，拟合度明显上升。除去第33-35 个月实际储量有较大幅度上升、预测数据没有上升到相应高度以外，其余月份中两条曲线几乎完全重合。计算所得残差全部控制在0.6万吨以内、相对误差基本控制在5%，只有极个别值临近10%。作为预测模型，这样的误差完全可以接受，即已经达到了一个较为满意的预测水准。

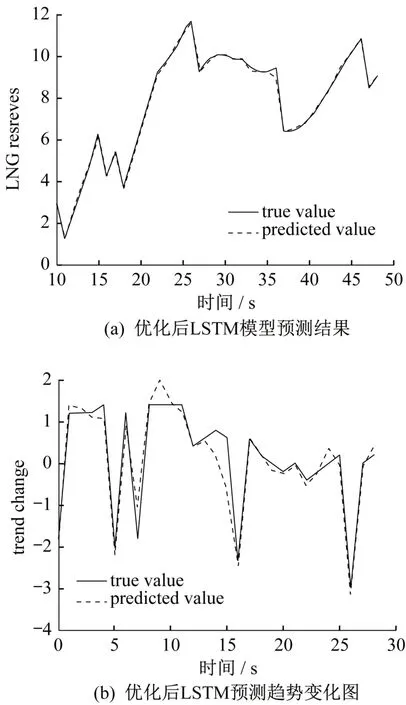
图3 完全优化后LSTM预测结果图Fig.3 The prediction of the completely optimized LSTM

将改进前后的预测结果进行量化对比，如表5所示。

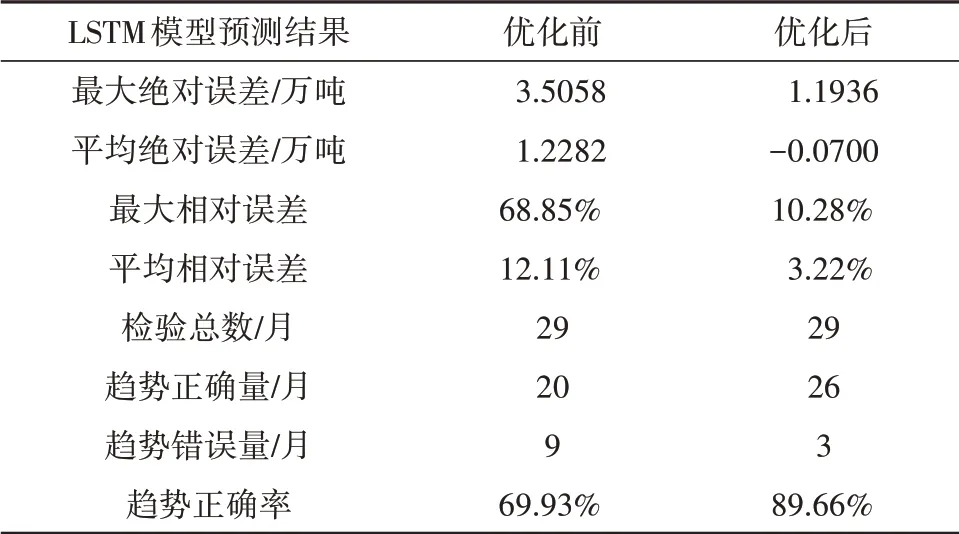
表5 优化前后预测结果对比Tab.5 The prediction comparison of initial and optimized LSTM

由表5 可以看出，预测效果较之前改善了很多。尤其是当后一个月比前一个月出现较大变化时，预测值不仅能与实际值保持同增同减，增减的幅度也近似相同。第5、16、26 个月这三个下降值较大的月份，变化程度甚至完全相同。在所有29 个月中，仅有3 个月的趋势与实际值不同，即预测趋势的准确值达到了89.66%，因为出现偏差的个别数值即使趋势不同，但相差也很小，可以忽略，也就是说达到了企业的基本运营要求。

4 总结

LNG储量受到汇率、政策、国家基础建设等诸多因素的影响。如何从已有信息中分析出有效信息辅助未来储量的预测，是每个投资者都想要寻找的办法。本文通过互信息的方法分析了LNG 影响因素的相关性和冗余性，建立了基于LSTM 神经网络的LNG 预测模型，并根据预测结果对LSTM 预测模型进行了优化，使其预测结果控制在较小的误差范围内，从而为LNG 储量计划提供指导。