化学势差对界面迁移下晶内微裂纹演化的影响

黄施茜，黄佩珍

（南京航空航天大学机械结构力学及控制国家重点实验室，江苏南京210016）

随着微电子技术不断发展，集成电路的特征尺寸不断减小。集成电路中的内连导线承担着传递电信号的重要作用，在复杂的工作环境下会出现各种各样的失效问题，其可靠性对集成电路的可靠性造成重大影响，成为科学界广泛研究的热点问题之一。

从上世纪六十年代起，人们就开始对集成电路内连导线进行实验观察［1-4］，并初步了解了金属内连导线的失效机制。在此基础上，发展出了大量的理论分析方法。随着计算机技术的发展，结合理论分析，数值模拟的方法逐渐成为内连导线微结构演化的主要研究方法。

基于Herring［5］经典理论，Suo［6］系统推导了界面迁移和表面扩散下微结构演化的基本理论和弱解描述，并对热蚀沟的形成和晶粒生长现象进行了简单的数值模拟。He 等［7-9］研究了应力、电场诱发表面扩散下晶内微裂纹的演化。Zhou 等［10-11］研究了内连导线线宽对梯度应力场和电场诱发表面扩散下晶内微裂纹演化的影响。近几年，相场法逐渐成为热门的数值模拟方法之一。李二丽等［12］用相场法模拟了在力场及热场作用下椭圆形孔洞的演化。孔涛等［13］研究了不同外场对孔洞形貌演化的影响规律并探讨了孔洞愈合机理的可行性。李海波［14］用相场法模拟了各向异性压电材料中夹杂和孔洞的演化。

从上述可以看出，对内连导线内部微裂纹演化的研究已经有了一定的实验、理论和数值基础，但是这些研究工作大多着眼于表面扩散下的微裂纹或微孔洞的演化。界面迁移下微结构演化的研究相对较少，仅见余文韬等［15］数值模拟了应力诱发界面迁移机制下的晶内及沿晶微裂纹演化路径。Jing等［16］数值模拟了夹杂-基体弹性模量比、初始形态比、外部应力和线宽对夹杂形态演化的影响。而界面迁移机制也是导致微结构形态演化的主要机制之一，至今未见电场诱发界面迁移机制下的微裂纹演化研究。

故本文基于Suo 推导的界面迁移机制下的微结构演化弱解描述，建立电场诱发界面迁移下的有限单元法，对晶内微裂纹的形貌演化进行数值模拟研究，主要探讨界面之间的化学势差对晶内微裂纹形貌演化的临界电场和形貌变化的影响。

1 二维晶内微裂纹的模型

图1 中晶内微裂纹形貌由初始形态比β0确定，其中，a和h0分别为微裂纹的长、短半轴长，V0为导线远端电场大小。假设电压在电场边界上均匀分布，电流在导体内部的流动符合欧姆定律；第三维的电场分量为零，且电场能和表面能互不影响。此外，假设晶体和环境之间的化学势差Δg不变。

图1 二维晶内微裂纹模型Fig. 1 Two-dimensional intragranular microcrack model

2 基本理论

2.1 弱解描述

界面迁移机制下，固体和环境之间的物质通过蒸发和凝结过程进行交换，从而使微结构的形貌发生改变。在这个过程中，微结构演化的驱动力主要来自表面能γs、电压V以及固相和气相之间的化学势差Δg，具体表达式为［8］

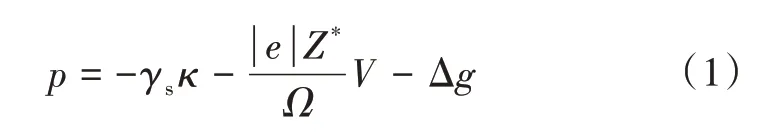
其中，κ为裂面表面曲率，在凸面上为正，e为元电荷，Z*为原子有效化合价，Ω为原子体积，V为原子所在点的电势。驱动力p大于零时，固体物质增加，驱动力p小于零时，固体物质减少。

在界面迁移的过程中，界面上的每一点都遵循运动学规律，即

式（2）中，vn为界面法向速度，m为界面迁移率。

系统的总自由能减少量为

式（3）中，δrn为界面法向虚位移。

将式（2）代入式（3），得到界面迁移的弱解描述为

2.2 有限元方法

由于本文讨论的是二维问题，故利用图2 所示的线性单元离散微裂纹表面形状。整个裂面系统的运动可由单元上各节点的运动得到。

图2 线性单元Fig. 2 A linear element

单元长度为l，倾角为θ，节点1、2 的坐标分别为(x1，y1)、(x2，y2)，法向量为n= (sinθ，- cosθ)。

由于微裂纹系统受表面能、电势能和化学势差的作用，故线性单元的自由能增量为

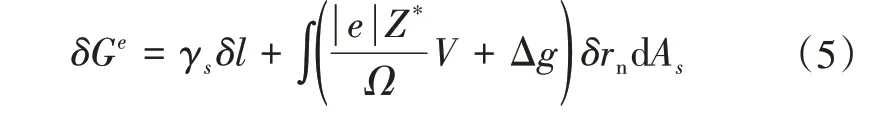
将式（5）进行积分，得出有限元的控制方程为

式（6）中，He为粘度矩阵，xe为广义速度矩阵，f e为广义力矩阵。

3 数值计算与讨论

基于以上所建立的有限元控制方程，利用Fortran语言编制相应的有限元程序，重点讨论化学势差对界面迁移机制下内连导线中晶内微裂纹演化的影响。本文取铜为研究材料，采用无量纲参数，即电势能与表面能相对大小χ=V0||e Z*h0Ωγs，无量纲时间t=tmγsh20，无量纲化学势差Δg= Δgh0γs。

3.1 化学势差对微裂纹演化过程的影响

图3 中给出了初始形态比β0= 4，χ= 0.2 时，不同化学势差Δg下晶内微裂纹的演化图。由图3（a）可知，当Δg= -0.058 时，化学势差小于零，即环境的化学势高于晶体的化学势，物质由气相进入固相中，有利于微裂纹收缩。此时，由于驱动力p大于零，固体物质增加，驱使晶粒向内生长，裂面朝着远离固体的方向运动，微裂纹发生收缩，并且最终趋于圆形。当Δg=0.29时，虽然化学势差大于零（即环境的化学势低于晶体的化学势），物质由固相进入气相中，有利于微裂纹向外发生扩展。但系统驱动力p仍旧大于零。因此，在微裂纹演化的初期，微裂纹的短轴向外扩展，而长轴依旧保持向内收缩，同时微裂纹不断趋于圆柱化（图3（b））。随着化学势差的增大，系统驱动力p小于零，导致物质从固相进入气相，微裂纹向外发生扩展，如图3（c）所示。在微裂纹发生扩展演化的初期，短轴发生扩展，长轴先向内收缩而后向外发生扩展。在此过程中，短轴发生扩展的速度要大于长轴发生扩展的速度，最终也将趋于圆形，而后保持圆形向外扩展。

由图3 可以看出，不管是扩展还是收缩，在表面能、电势能和化学势差的共同作用下，晶内微裂纹都将趋于圆形，即晶内微裂纹的形态比β都将趋近于1，下面详细探讨化学势差对微裂纹形态比的影响。

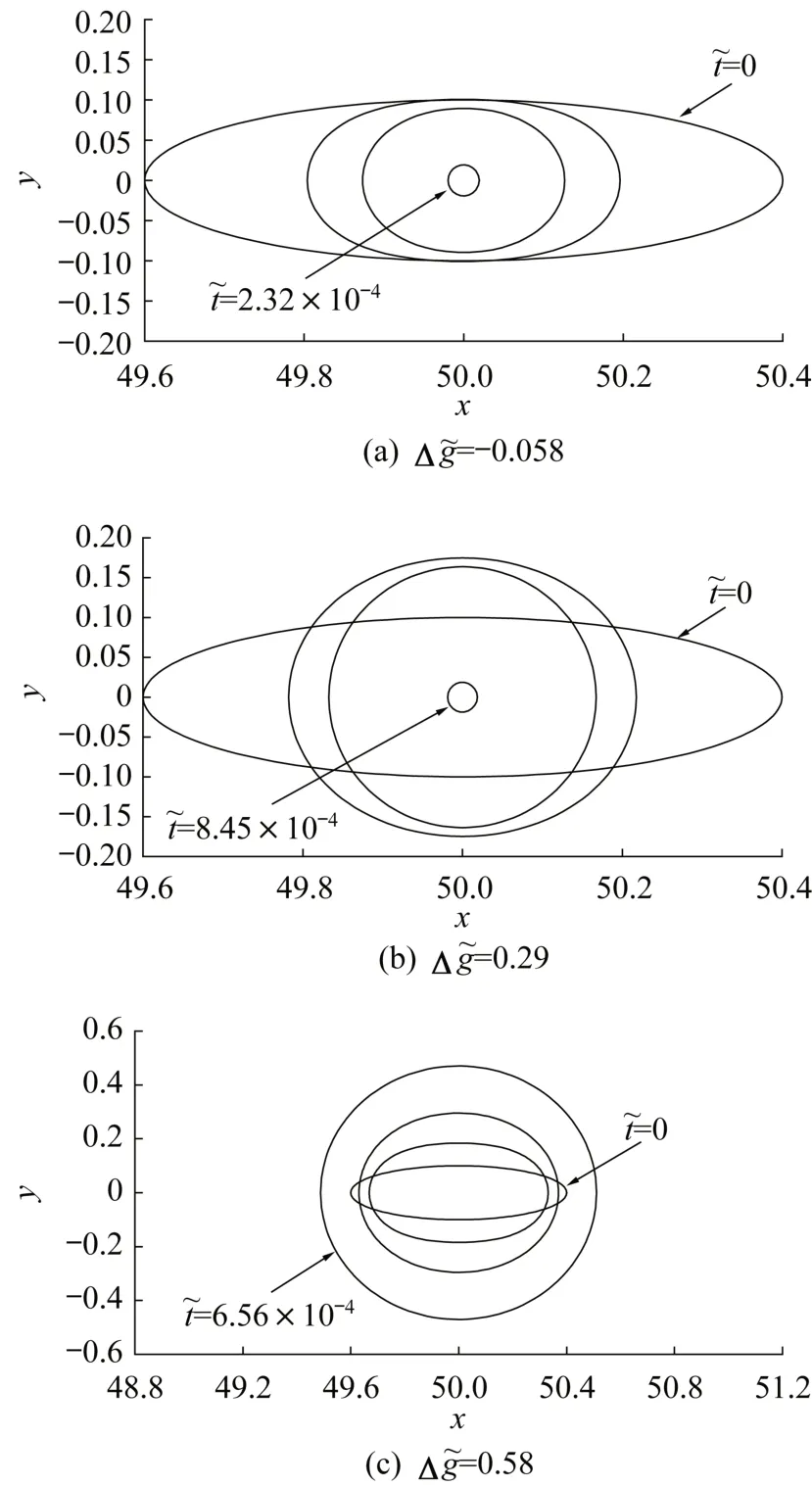
图3 β0 = 4，χ = 0.2时的晶内微裂纹演化图Fig. 3 Evolution of intragranular microcracks for β0 = 4,χ = 0.2

3.2 化学势差对形态比的影响

图4 所示为初始形态比β0= 4 的晶内微裂纹演化过程中形态比β随时间的变化图。由图4（a）可以看出，在其他条件相同而化学势差不同的情况下，微裂纹圆柱化时间随着Δg的增大而增大，也就是说Δg阻碍微裂纹的圆柱化。但随着电场的增大，削弱了Δg对微裂纹圆柱化过程的影响（图4（b））。

图4 β0 = 4的微裂纹形态比随时间变化图Fig. 4 The aspect ratio as a function of time for the microcrack with the initial aspect ratio β0 = 4

通过大量的数值模拟分析发现，在给定初始形态比β0和化学势差Δg的情况下，随着电场的不同，晶内微裂纹的演化也存在着如图3 所示的扩展和收缩现象，并存在临界电压χc。当χ＜χc时，晶内微裂纹发生收缩；当χ≥χc时，晶内微裂纹发生扩展。下面详细讨论化学势差Δg对临界电压χc的影响。

3.3 化学势差对临界电压的影响

图5 所示是不同初始形态比下临界电压随化学势差的变化图。由图5 可见，化学势差对临界电压的影响近似呈线性。且在相同条件下，化学势差越大，临界电压越小，即在晶体与环境的化学势差较大时，需要较小的电压便可使晶内微裂纹发生扩展。说明在同时考虑表面能、化学势差和电势能影响下的晶内微裂纹演化过程中，当Δg＜0 时，化学势差和表面能共同作用，与电势能相竞争，促使微裂纹发生收缩；当Δg＞0 时，化学势差和电势能共同作用，与表面能相竞争，促使微裂纹发生扩展。晶内微裂纹演化的过程是三者相互竞争的结果，且初始形态比越大，则微裂纹发生扩展所需的临界电压χc越小，说明初始形态比越大微裂纹更易发生扩展。

图5 不同初始形态比下的临界电压随化学势差的变化Fig. 5 The critical voltage as a function of the difference ofchemical potential at the different initial aspect ratio

4 结论

本文有限元模拟了电场下晶内微裂纹的演化，详细讨论了化学势差、形态比和电场对微裂纹演化的影响，得出以下结论。

（1）化学势差Δg对晶内微裂纹的形貌演化过程有着显著影响。

（2）相同条件下，Δg越大，则晶内微裂纹圆柱化所需时间更长，即Δg对晶内微裂纹的圆柱化有一定的抑制作用。

（3）当Δg＜0 时，化学势差和表面能共同作用，与电势能相竞争，促使微裂纹发生收缩；当Δg＞0 时，化学势差和电势能共同作用，与表面能相竞争，促使微裂纹发生扩展。