直辐板车轮阻尼脊肋结构减振性能分析

崔 越，周 信，鲁锦涛，王安斌

（上海工程技术大学 城市轨道交通学院，上海 201620）

目前我国城市交通建设发展迅猛，因城市轨道交通具有速度快、运量大、准点率高等特点，已经成为我国各城市居民日常出行中必不可少的交通工具，但在为居民生活带来方便的同时，列车运行造成的振动噪声问题也是当前急需解决的一大问题。轮轨噪声在运行速度相对较低的城市轨道交通中占据主导地位，在车轮上敷设阻尼装置是降低轮轨振动噪声的一种有效的主动减振降噪手段，目前主要有3种阻尼装置用来减少列车的噪声，分别是层状约束阻尼、摩擦阻尼装置以及调谐质量阻尼器，阻尼装置的减振降噪原理是：阻尼层通过剪切变形、干摩擦等手段将振动能转变成热能耗散出去，以达到减振降噪的目的[1]。

近年来国内学者对阻尼车轮降噪效果和优化进行了大量的研究。何宾等[2－4]将约束阻尼车轮简化成圆板，运用有限元与边界元法分析了周向阻尼脊肋的形状、铺设方式、面积等对减振降噪效果的影响，为约束阻尼层形状优化提供新的思路。刘玉霞等[5]研究了喷涂式阻尼和层状约束阻尼的车轮振动声辐射特性，研究结果表明层状约束阻尼降噪效果更好。周信等[6]分析了喷涂阻尼厚度对斜曲型和双S 型车轮振动声辐射特性的影响。田晓琳[7]尝试使用阻尼割缝和声学黑洞方法，优化约束阻尼车轮的减振降噪性能。肖玉兰等[8]研究了黏弹性约束阻尼车轮3个主要参数对车轮振动影响的显著性和主次顺序。陈彦恒等[9]研究表明，阻尼材料对车轮模态振型影响不大，车轮各位置在不同激励下的主要模态也各有不同，但在各种情况下阻尼材料均有一定减振降噪效果。钱鼎玮等[10]研究了辐板阻尼层厚度对车轮振动声辐射特性的影响。

对于轨道交通轮轨结构噪声，其噪声辐射往往随着振动的减弱而降低，故本文主要关注阻尼车轮的减振效果。首先通过对比普通刚性车轮和层状约束阻尼车轮之间谐响应分析结果，研究层状约束阻尼车轮的减振效果和减振特点；然后在前人研究阻尼脊肋车轮的基础上，建立半圆形阻尼脊肋车轮仿真模型并进行谐响应分析，分析阻尼脊肋半径对减振效果的影响；最后在阻尼脊肋车轮的理论基础上，提出减振效果更好的阻尼车轮设计方案，并建立仿真模型，验证新型阻尼车轮的减振效果。

1 车轮动态特性有限元计算模型

本文使用直径为840 mm的直辐板车轮，车轮有限元网格如图1所示。

图1 直辐板车轮有限元网格

在车轮辐板上附加的约束阻尼层截面如图2所示。在ANSYS 中定义车轮及阻尼层的材料性能参数，各材料参数见表1。对轮毂孔施加固定约束，并在车轮踏面名义滚动圆接触点施加轴向单位力以模拟车轮在实际运行时的受力状态。约束层厚度为1 mm，阻尼层厚度为1.5 mm。车轮的模态分析方法选用Block Lanczos 法；谐响应分析选用完全法，分析范围为0～3 000 Hz，步长取为20 Hz。

图2 层状约束阻尼层截面

表1 材料参数

2 车轮动态特性计算分析

2.1 模态分析结果

通过模态分析计算结构的固有频率，避免结构产生共振。普通刚性车轮与层状约束阻尼车轮的固有频率对比如图3 所示，可见在车轮辐板铺设层状约束阻尼，对车轮固有频率和模态振型的影响很小。

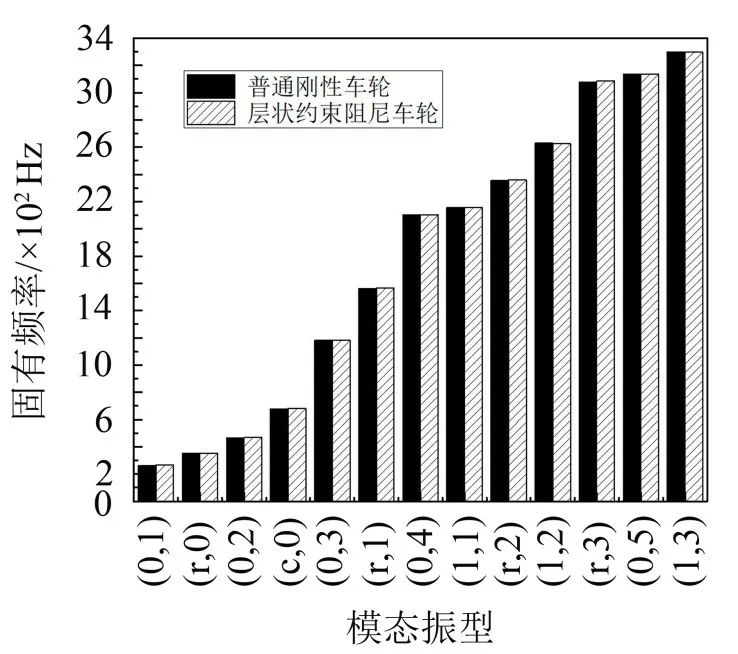
图3 普通刚性车轮与层状约束阻尼车轮的固有频率对比图

2.2 谐响应分析结果

通过谐响应分析计算车轮在受到周期性简谐载荷激励时的稳态响应。使用完全法计算得刚性车轮与层状约束阻尼车轮在踏面名义滚动圆接触点的位移导纳，并对数据进行处理得到该点的速度导纳，如图4所示。

由图4 可知，层状约束阻尼能够减少车轮大部分固有频率处的振动，但是在2 360 Hz 处振动速度级增加约4.6 dB。

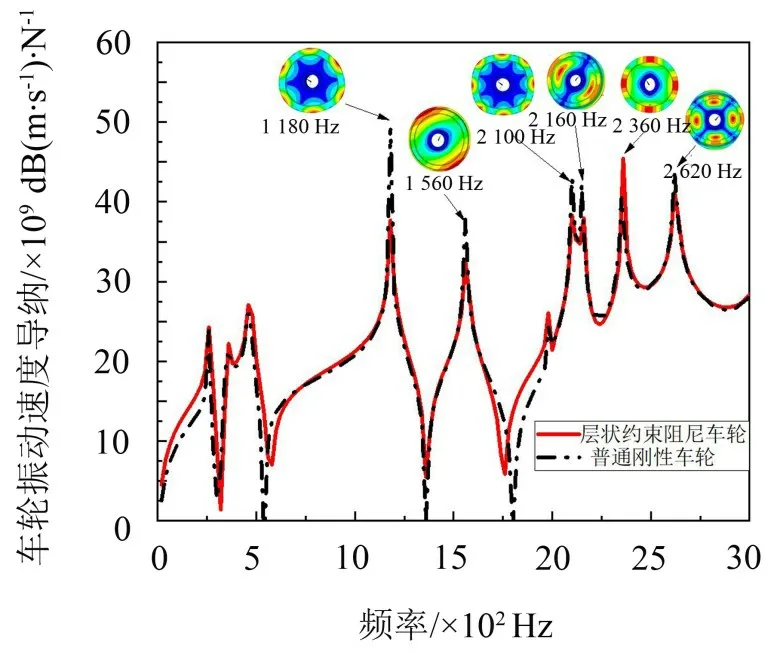
图4 无阻尼车轮与层状约束阻尼车轮速度导纳图

3 车轮添加阻尼脊肋减振效果分析

由上节内容可知，在车轮辐板上附加约束阻尼层能够减小车轮在大部分固有频率处的振动，但在在2 360 Hz 频率处，振动反而有所增加。为了更好地降低总的轮轨噪声，根据该模态振型下的模态应变能分布规律铺设阻尼脊肋[3]。

层状约束阻尼车轮在2 360 Hz处对应的模态应变能云图和剪应变分布云图分别如图5 和图6 所示。通过在该模态的最大模态应变能处（即辐板半径1/3 位置处）布置阻尼脊肋，增加模态最大应变能处黏弹性层的厚度，耗散系统更多的能量，来降低2 360 Hz频率下的振动。

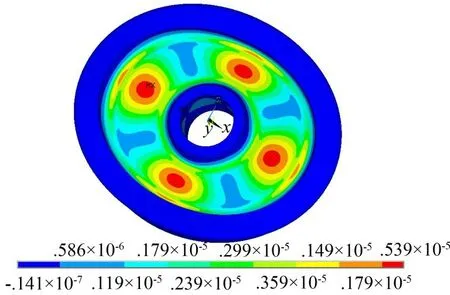
图5 2 360 Hz处的模态应变能云图

图6 2 360 Hz处的剪应变分布云图

3.1 布置脊肋后的优化效果

在辐板半径1/3位置处布置半径为6 mm的半圆形阻尼脊肋，研究表明在内约束层添加脊肋能进一步优化阻尼脊肋的减振降噪效果[3]，故在阻尼脊肋的内约束层设置半径为4.5 mm的内约束层脊肋，阻尼脊肋的横截面如图7所示。将阻尼脊肋车轮的谐响应分析结果与层状约束阻尼车轮进行对比，确定优化效果。车轮振动速度导纳的结果对比如图8所示。

图7 半径为6 mm的半圆形脊肋截面

图8 附加半径为6 mm的半圆形脊肋后的速度导纳图

由图8 可知在附加半径为6 mm 的半圆形脊肋后，阻尼车轮在2 360 Hz 频率处的振动速度级降低约2.2 dB，表明在模态最大应变能处添加阻尼脊肋能减小该模态处的车轮振动幅值，但该阻尼脊肋在半径为6 mm时减振效果并不明显，主要原因是该阻尼脊肋的横截面积太小，黏弹性材料剪切应变耗散的能量太少，不足以抑制该模态的振动，故采用增加阻尼脊肋横截面积的方法，加强阻尼脊肋的减振效果[3]。

3.2 不同横截面积阻尼脊肋的对比

为了优化半圆形阻尼脊肋车轮的减振降噪效果，得到减振降噪效果最好的阻尼脊肋半径值，对阻尼脊肋半径进行定量分析。

首先选取半径为10 mm、15 mm、20 mm 的半圆形阻尼脊肋作为基准进行对比分析。同时为了避免实际的安装使用时与其他部件产生碰撞冲突，将20 mm选定为最大阻尼脊肋半径取值，4种半径阻尼脊肋的速度导纳对比如图9所示。

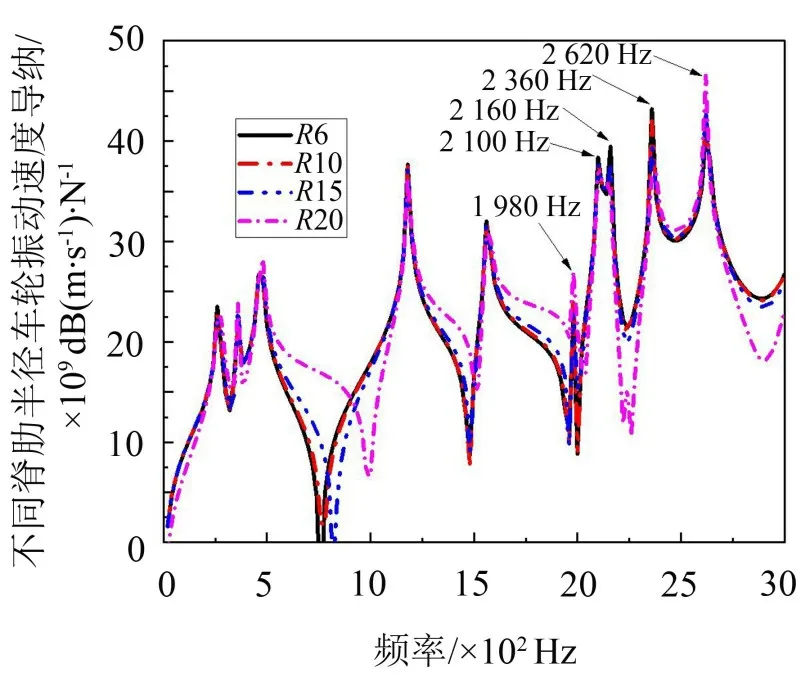
图9 半径为6 mm、10 mm、15 mm和20 mm半圆形脊肋车轮速度导纳对比图

由图9可知，阻尼脊肋半径的改变对5个频率处的振幅影响较大，分别为1 980 Hz、2 100 Hz、2 160 Hz、2 360 Hz 和2 620 Hz 处，在各个频率处的振动随阻尼脊肋半径变化规律如下：

（1）1 980 Hz 处的振动幅值在半圆形脊肋半径为10 mm时上升，15 mm时下降，在20 mm时上升，振动幅值最小值出现在半径6 mm处，最大值在半径20 mm处；

（2）2 100 Hz 处的振动幅值随着半圆形脊肋半径的增大而减小，振动幅值最小值出现在半径20 mm处，最大值出现在半径6 mm处；

（3）2 160 Hz 处的振动幅值在半圆形脊肋半径为10 mm 时下降，15 mm 时上升，在20 mm 时下降，振动幅值最小值出现在半径20 mm 处，最大值出现在半径6 mm处；

（4）2 360 Hz 处的振动幅值随着半径的增大而减小，振动幅值最小值出现在半径20 mm处，最大值出现在半径6 mm处；

（5）2 620 Hz 处的振动幅值随着半径的增大而增大，振动幅值最小值出现在半径6 mm 处，最大值出现在半径20 mm处。

在4 种半径取值中，当半圆形阻尼脊肋半径为15 mm时，总的振动幅值最小，但由于此时各脊肋的半径间隔相差较大，故进一步计算脊肋半径为8 mm、12.5 mm和17.5 mm时车轮的振动速度导纳，缩小脊肋半径的选取范围。阻尼脊肋半径为6 mm、8 mm、10 mm、12.5 mm、15 mm、17.5 mm 和20 mm 时的半圆形阻尼脊肋车轮在1 980 Hz、2 100 Hz、2 160 Hz、2 360 Hz 和2 620 Hz 处的速度导纳对比如图10所示。

由图10 可知，阻尼脊肋半径为8 mm 的半圆形阻尼脊肋车轮在2 360 Hz 处出现共振峰，阻尼脊肋半径为12.5 mm 的半圆形阻尼脊肋车轮在2 160 Hz处出现共振峰，阻尼脊肋半径为20 mm的半圆形阻尼脊肋车轮在2 620 Hz处出现共振峰，同时2 620 Hz处的振动幅值满足随着半圆形脊肋半径的增大而增大的规律。

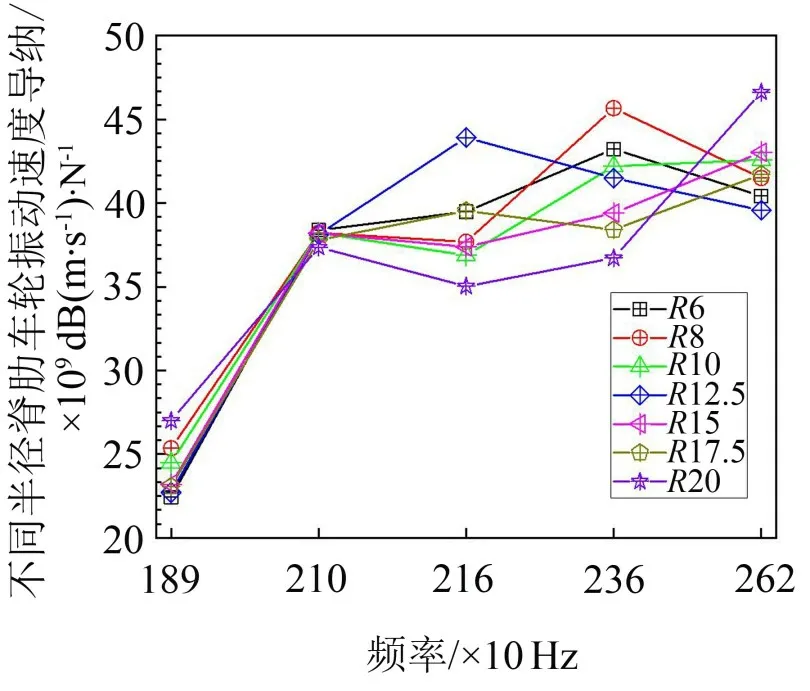
图10 半径为6 mm～20 mm半圆形脊肋在敏感频率处车轮振动速度导纳对比图

由图10可知，虽然1 980 Hz处的振动幅值随阻尼脊肋半径的变化而改变，但由于其幅值的量级很小，所以对车轮总体振动幅值影响也很小，故后文将重点放在振动量级较大且振动幅值变化较为明显的固有频率处，即2 100 Hz、2 160 Hz、2 360 Hz 和2 620 Hz频率处。

对图10中的数据综合比对后可知，减振效果最好的脊肋半径取值最有可能出现在半径15 mm～17.5 mm 之间。考虑到施工安装时的精确度，以0.5 mm为间隔，在半径15 mm～17.5 mm范围中进一步求解。对15.5 mm、16 mm、16.5 mm、17 mm 半径的半圆形阻尼脊肋车轮进行谐响应分析，各半径条件下的半圆形阻尼脊肋车轮的速度导纳结果对比如图11所示。

图11 半径为15 mm～17.5 mm半圆形脊肋在敏感频率处的速度导纳对比图

由图11 可知，脊肋半径在15 mm～17.5 mm 之间的半圆形阻尼脊肋车轮在2 100 Hz和2 360 Hz处的振动幅值比较相近，且振动幅值有随脊肋半径增大而减小的趋势；在2 160 Hz 处，脊肋半径为16 mm、17 mm 和17.5 mm 时，振动幅值明显较高；在2 620 Hz 处，半径为15 mm 和16.5 mm 时振动幅值明显较高。故在半径为15.5 mm 时，阻尼脊肋车轮的减振效果最好，而在半径为16 mm时效果次之。

由以上谐响应分析结果判断15.5 mm～16 mm为840刚性车轮附加层状阻尼后减振降噪效果最好的半圆形阻尼脊肋半径取值范围。半径为15.5 mm的阻尼脊肋车轮与层状约束阻尼车轮的速度导纳对比如图12所示。

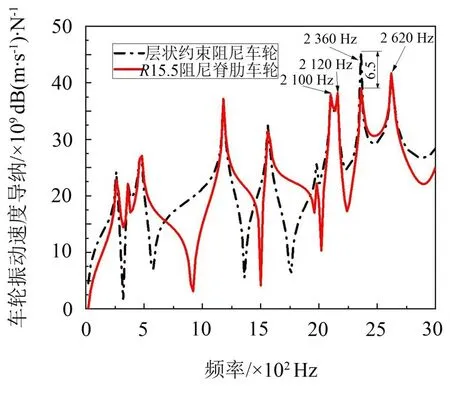
图12 附加半径为15.5 mm的半圆形脊肋后的速度导纳图

由图12 可知，半径为15.5 mm 的半圆形阻尼脊肋后在2 100 Hz和2 360 Hz处的振动速度级分别降低约0.5 dB 和6.5 dB，在21 60 Hz 和2 620 Hz 处的振动速度级分别增大约0.2 dB和0.4 dB，在这4个频率下的总振动速度级降低约2.3 dB。相较于制作阻尼脊肋所需的材料与安装半径过大的阻尼脊肋所可能产生的问题，半径为15.5 mm 的阻尼脊肋的减振效果并不理想，故考虑对阻尼脊肋进行优化，在其基础上设计新型的阻尼车轮。

4 新型阻尼车轮设计

延续阻尼脊肋车轮在车轮模态振型应变能最大处布置阻尼脊肋，可通过吸收该处振动能来减小车轮振动的思想，设计新式的阻尼车轮。约束阻尼层主要是通过受两边弹性面层约束的黏弹性阻尼层的剪切变形，耗散振动的能量，达到减振降噪的目的，所以本设计的主要思想是：为阻尼脊肋的剪切变形提供更充足的空间，减少阻尼层受到的约束，使阻尼层更易产生剪切变形，增加阻尼层耗散的车轮振动能量。

新型阻尼车轮命名为桥式阻尼车轮，该车轮的阻尼脊肋为12×5 mm的矩形，截面积与半径为6 mm的半圆形阻尼脊肋基本相同。矩形阻尼脊肋的长边与车轮振型最大应变能处接触，采用矩形脊肋，是为了方便阻尼脊肋与两边约束阻尼层的连接。桥式阻尼脊肋与普通矩形阻尼脊肋的不同之处是：桥式阻尼脊肋与两侧层状约束阻尼的连接点位于矩形阻尼脊肋的上端部，车轮辐板处的约束阻尼层处于悬空状态，使阻尼脊肋和两侧辐板处的约束阻尼层更易发生剪切变形，以此增强约束阻尼层的减振效果。

新型阻尼脊肋车轮如图13所示，同时为了排除阻尼脊肋形状对减振效果的影响，建立12 mm×5 mm 普通矩形脊肋车轮模型进行对比，矩形阻尼脊肋车轮如图14所示。3种层状阻尼脊肋车轮的速度导纳结果对比如图15所示。

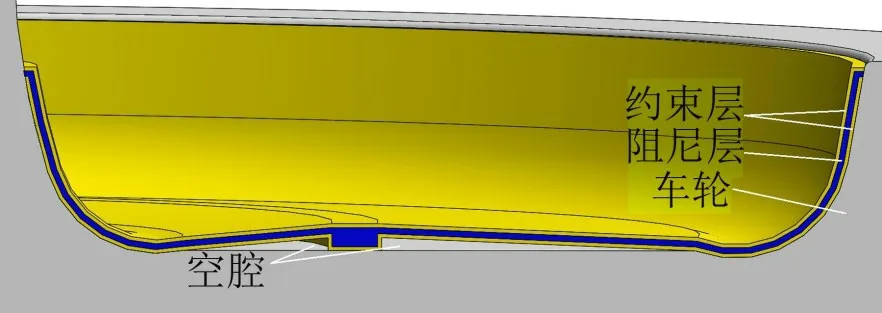
图13 12×5 mm桥式阻尼脊肋截面

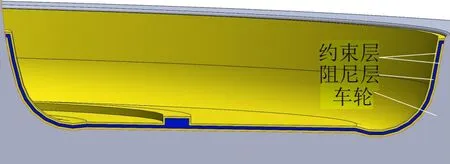
图14 12×5 mm矩形脊肋截面

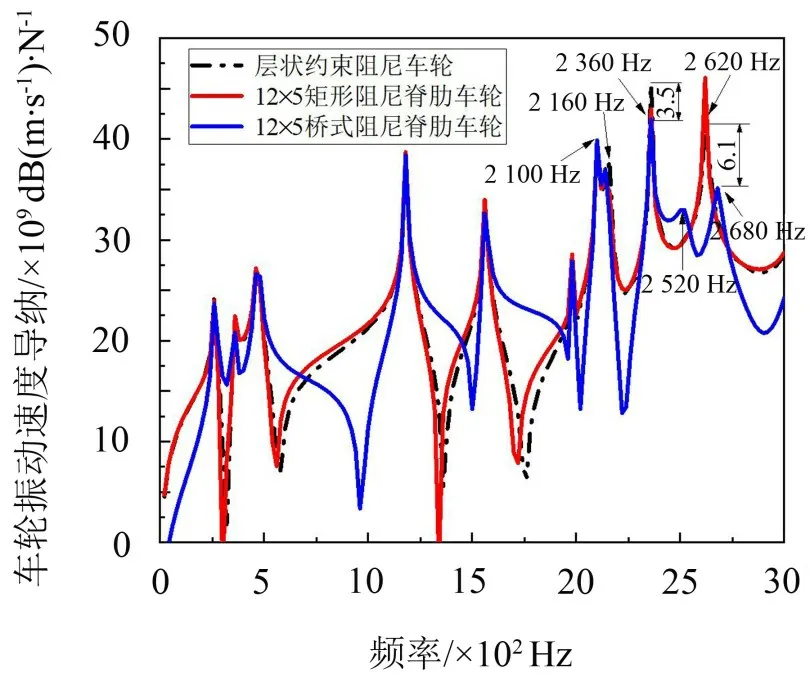
图15 层状约束阻尼车轮、矩形和桥式阻尼脊肋车轮振动速度导纳对比图

由图15 可知，相较于层状约束阻尼车轮，矩形阻尼脊肋降低了2 360 Hz 处的车轮振动幅值，但是同时大幅提升了2 620 Hz 处的振动幅值，故普通矩形脊肋无法达到很好的减振效果。

桥式阻尼脊肋在2 160 Hz和2 360 Hz处的振动速度级分别减低约0.9 dB和3.5 dB，同时2 620 Hz处的振动幅值偏移至2 680 Hz 附近，振动速度级降低约6.1 dB；在2 100 Hz 处的振动速度级上升约1.6 dB，并且在2 520 Hz 处产生新的振动峰值使该频率振动速度级上升2.6 dB。桥式阻尼脊肋车轮在这5个频率下的总振动速度级降低约2.4 dB，与半径为15.5 mm 的半圆形阻尼脊肋车轮相当，可见桥式脊肋车轮在脊肋横截面积较小的情况下，减振效果更好。

5 结语

本文使用有限元方法对直辐板车轮进行模态分析和谐响应分析。在普通直辐板车轮上附加约束阻尼层，分析约束阻尼层的减振效果及特性，结合模态分析和谐响应分析结果，采用半圆形阻尼脊肋进一步优化约束阻尼层的减振效果，并探究阻尼脊肋横截面积对车轮减振效果的影响。在阻尼脊肋和约束阻尼层减振降噪理论基础上，提出采用桥式阻尼脊肋约束阻尼层进行减振的方法，并对减振效果进行计算，得到以下结论：

(1)在直辐板车轮上附加约束阻尼层，能够减小车轮在大部分固有频率处的振动；

(2)在模态最大应变能处添加半圆形阻尼脊肋，能够降低该模态下的振动，当半圆形脊肋的半径为15.5 mm时减振效果最好；

(3)桥式阻尼脊肋通过悬空车轮辐板处的层状阻尼，使阻尼脊肋和辐板处的黏弹性阻尼层更易发生剪切变形以耗散振动能，增强减振效果。脊肋横截面积为12×5 mm 的桥式阻尼脊肋与半径为15.5 mm的半圆形阻尼脊肋减振效果相当。