变工况下滚动轴承双谱分析及智能故障诊断

张锐戈，肖荣辉，高忠坚

(1.三明学院 机电工程学院，福建 三明 365004；2.装备智能控制福建省高校重点实验室，福建 三明 365004)

滚动轴承是旋转机械的关键零部件，也是故障率较高的一类部件[1]。工况恒定时，通过特征频率比对或特征参数辩识能判别故障类型[2]。工况变化时，会产生特征频率模糊[3]和特征参数统计特性变化[4]现象，导致故障诊断困难甚至造成误判。工程实践中旋转机械常以变工况方式运行，如风机和采矿设备的转速波动[5]，机床为抑制切削颤振改变运行工况[6]。因而开展变工况故障诊断研究对旋转装备工程实践具有重要意义。

频谱诊断法通常采用阶次追踪技术处理特征频率模糊问题。硬件阶次追踪使用编码器[7]或键相信号[8]采集转速信息，通过角度域重采将等时间间隔的非平稳信号转变为等角度间隔平稳信号，进而将随转速变化的故障特征频率转化为恒定的故障特征阶次。软件阶次追踪是从振动信号中恢复转速信息，有瞬时频率提取和瞬时故障特征频率计算两种方式。前者将信号变换到时频域后采用单一成分隔离和相位解调[9]等手段获得转速信息，后者利用故障特征频率与转速间的比例关系间接恢复转速信息，也称为故障特征阶次法[10]。

变工况智能故障诊断方面，采用阶次追踪与模式识别相结合、迁移学习和特征选择等方法克服特征参数扰动。阶次追踪智能诊断是先对信号进行角度域重采，再提取频谱峰值[11]、阶次谱[12]等频域参数，或提取均值、方差[13]等时域参数训练诊断模型；迁移学习是采用领域自适应[14]、模型微调[15]和深度学习[16]等手段，迁移不同工况间的信息提升诊断模型性能；特征选择法采用扰动属性投影[17]和奇异值分解[18]等算法选择重要的特征向量抑制特征参数的变工况扰动。

滚动轴承振动信号受强噪声干扰，双谱凭借良好的高斯噪声抑制[19]和系统非线性特征提取[20]能力在故障诊断领域得到应用。双谱切片[21]、频移双谱[22]、二值双谱[23]以及阶次分析[24]、2 阶全变分去噪[25]、奇异值分解[26]与双谱相结合等方法，皆能提取轴承故障特征信息。从文献检索结果来看，目前还没有工况变化情形下双谱特性的研究成果报道。

从诊断思路来看，已有诊断方案过程较为复杂，还存在精度受限[27]、参数选择不易[28]和知识负迁移[29]等问题。因而提出新的诊断思路，直接提取工况变化不敏感特征参数，无需预处理环节，使诊断过程简单易实施。滚动轴承结构不随工况变化，具有恒定的内在属性，轴承振动也具有明显非线性特点，因而采用双谱分析方法提取轴承振动特征和系统不变特性[30]。先基于滚动轴承振动信号模型推导双谱表征，探究双谱信号与工况变化及故障类型之间关联，并通过仿真和实测数据验证双谱工况不敏感特点，最后基于K近邻算法提出变工况诊断方案并进行验证。

1 变工况下滚动轴承振动信号双谱特性

1.1 滚动轴承振动加速度信号模型

故障情形下，滚动体通过缺陷部位周期性激励机械系统，输出具有调制特性的振动加速度信号[31]：

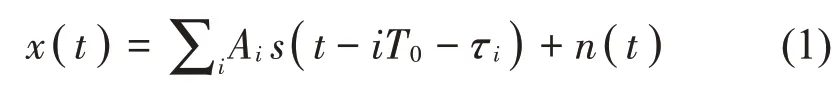
式中：Ai为幅度项，s(t)表示衰减振荡成分，n(t)为加性随机噪声。T0表示冲击激励周期，τi为T0的微小随机波动。幅度项Ai和振荡衰减项s(t)分别表示为[32]：

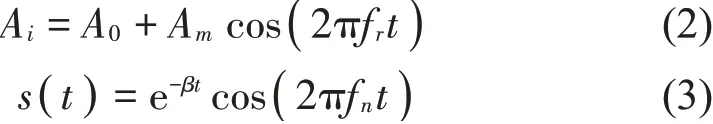
式中：A0和Am分别为固有载荷和变化载荷参数，fr为轴转动频率。式(3)中，β和fn分别为轴承系统的振荡衰减系数和固有共振频率。

根据滚动轴承结构特点，结合故障点、滚道和滚动体之间的位置关系，可知振动加速度信号和故障类型及运行工况间存在关联：

(1)振荡衰减成分由故障类型参数确定

s(t)由参数T0、β和fn确定。故障类型不同时，冲击激励间隔、激励位置皆不相同，在轴承系统中产生的衰减性质也不相同。即激励周期T0、振荡衰减系数β和固有振荡频率fn随故障类型不同发生变化，因而故障类型参数决定振荡衰减成分波形。

(2)幅度项取值由工况参数确定

幅度项Ai取值由参数A0、Am和fr确定。故障类型相同、工况不同时，参数A0、Am随载荷发生变化，fr随转速发生变化，但与故障类型相关的参数不发生变化。因而工况相关参数决定幅度项Ai取值。

1.2 滚动轴承双谱分析

一维信号x(t)的双谱定义为[33]：

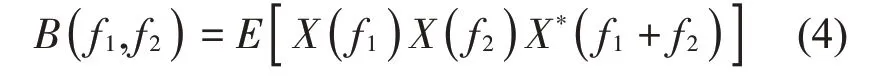
式(4)中，E表示数学期望，X(f)为x(t)的傅立叶变换，X*(f)表示X(f)的共轭。

将式(4)用傅立叶变换表征，有：

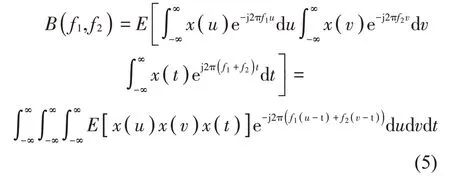
将式(1)所示信号模型代入式(5)。不失一般性，设随机序列τi的概率密度函数为φτ(t)，n(t)为零均值加性噪声，有：

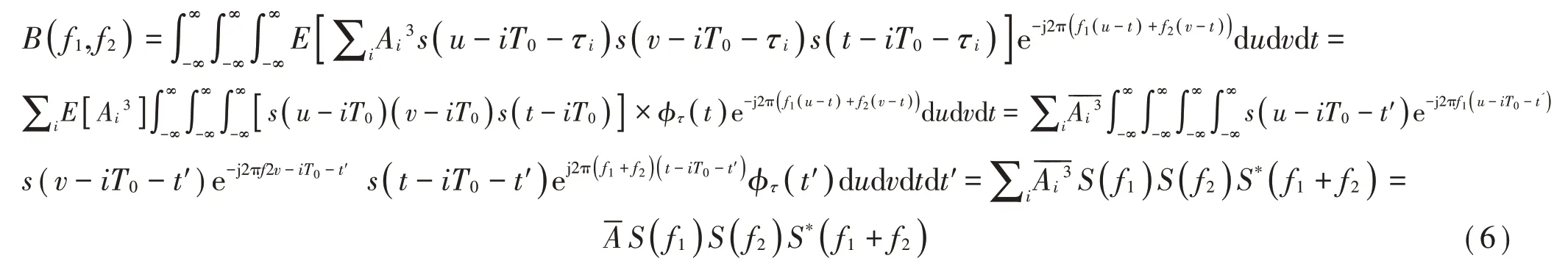
(1)不同工况下相同故障双谱具有较大相似性

由振动信号模型可知，当故障类型相同、工况不同时，衰减振荡项s(t)在同种故障下保持相似，仅幅度项Ai随工况发生变化。因而式(6)所示双谱S(f)相关项在相同故障时保持相似，仅随工况变化，双谱表现出较大的相似性。

(2)不同故障双谱具有较大差异性

依据振动信号模型，故障类型不同时，衰减振荡成分s(t)随故障发生变化，式(6)所示双谱S(f)相关项随之发生变化，双谱表现出较大差异性。

2 基于K近邻算法的变工况智能故障诊断

2.1 K近邻算法原理

K近邻算法基本思想[34]：就给定的训练数据集，寻找K个与新输入实例最邻近的实例，基于K个实例所属类别确定新输入实例的类别。

训练数据集可表示为

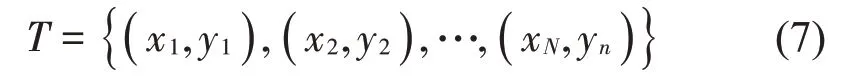
式中：xi∈X⊆Rn为实例的n维特征向量，表示为为特征向量的类别标签。

新输入实例的特征向量xj与训练集特征向量xi间的距离为

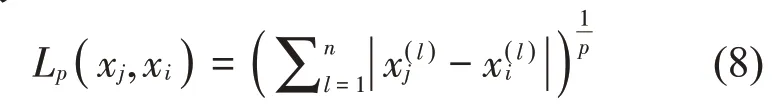
式中：p为距离指标参数，p=2时为欧氏距离。

依式(8)所示距离测度，在训练集中寻找与xj距离最邻近的K个特征向量，称为xj的邻域并记作NK(xj)。在邻域中依据多数表决分类规则决定xj的类别y：

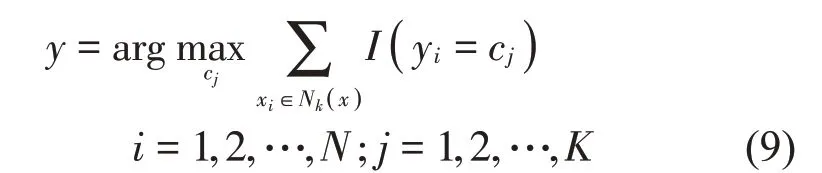
式中：I为指示函数，yi=cj时取值为1，否则取值为0。

2.2 基于双谱和K近邻算法的变工况故障判别

数据集特征向量和类别标签依下述方法设置：

(1)特征向量

取双谱元素幅值。每一列作为一个特征向量，第i个特征向量表示为为双谱第i列第l个元素的幅值，其中i=1,2,…,N。

(2)数据标签

分别用数字0、1、2 和3 表征正常、滚动体故障、内圈故障和外圈故障4种轴承状态。

使用某一工况下的4 种轴承状态数据，构建训练数据集：

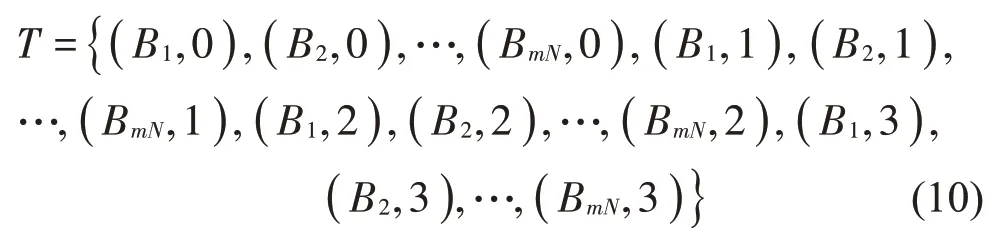
式中：m为构建训练集时每种轴承状态使用的双谱帧数。

辩识故障时，将未知工况、未知轴承状态的双谱作为新的实例，计算每一特征向量与训练集特征向量间的距离，选择K组距离最小数据，用多数表决规则判断当前特征向量所属标签类别。获得待辩识双谱N个特征向量类别标签后，再对其使用多数表决规则，结果为当前待辩识数据的故障类别。诊断过程如图1所示。

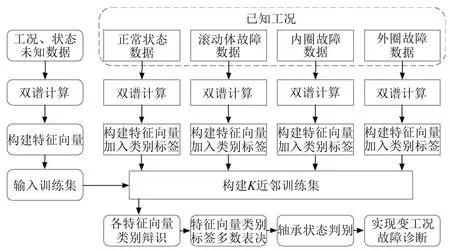
图1 变工况故障诊断流程图

3 实验研究

3.1 滚动轴承双谱特性仿真验证

仿真信号参数设置如表1 所示。第一、二行参数表征不同工况下相同故障振动加速度信号，第三行表征另一种故障仿真信号。使用零均值高斯随机噪声，幅值乘以系数0.15。仿真信号采样频率为500 Hz。

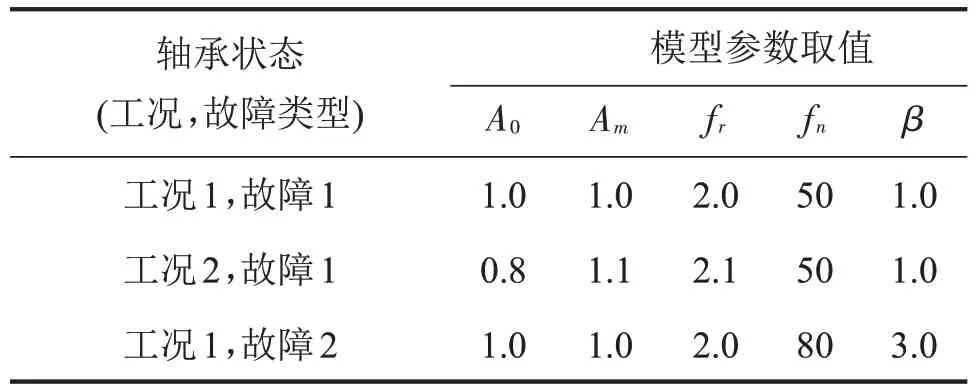
表1 仿真信号参数

双谱计算使用1 024个采样点数据片段，将其划分成长度为包含256 个数据点的子片段，各子片段间有192 个数据点重叠，用宽度为5 的Rao-Gabr 窗作频域平滑。后续实测信号和智能诊断的双谱用相同方法计算。

两种工况下相同故障仿真信号双谱如图2(a)和图2(b)所示，另一种故障双谱如图3所示。

图2 不同工况下相同故障仿真信号双谱

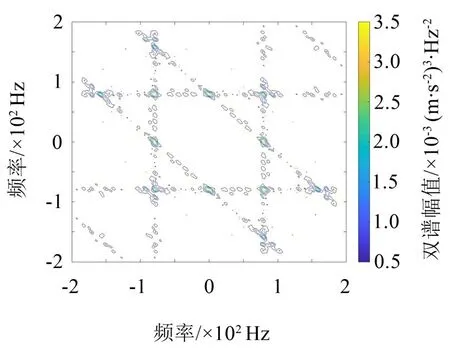
图3 第二种故障类型仿真信号双谱

详情如下：

图2(a)和图2(b)所示两幅双谱在(50 Hz,50 Hz)处出现双频率现象，此与表1中故障1的共振频率相吻合。图3 中(80 Hz,80 Hz )处的双频率也与故障2共振频率一致。这表明通过双谱分析能有效提取滚动轴承的振动特性，适合将双谱作为故障诊断特征参数。

图2(a)和图2(b)所示双谱在分布形状和幅值大小方面非常接近，表明双谱具有工况不敏感优点，适合作为变工况诊断特征参数。图3 与图2 中的两幅双谱在分布和幅值大小方面差异较大，表明双谱能有效表征滚动轴承故障类别，是一种有效的故障特征参数。

3.2 滚动轴承双谱实测数据验证

数据由凯斯西储大学轴承数据中心采集。实验装置如图4 所示[35]，测试对象为6205-2RS 深沟球滚动轴承，安装于电动机驱动端。轴承载荷、转速由扭矩传感器测量，用磁座方式安装加速度传感器，振动加速度信号的采样频率为12 kHz。

图4 轴承实验台布局

实验包含4种运行工况，载荷和转速皆不相同，参数如表2所示。

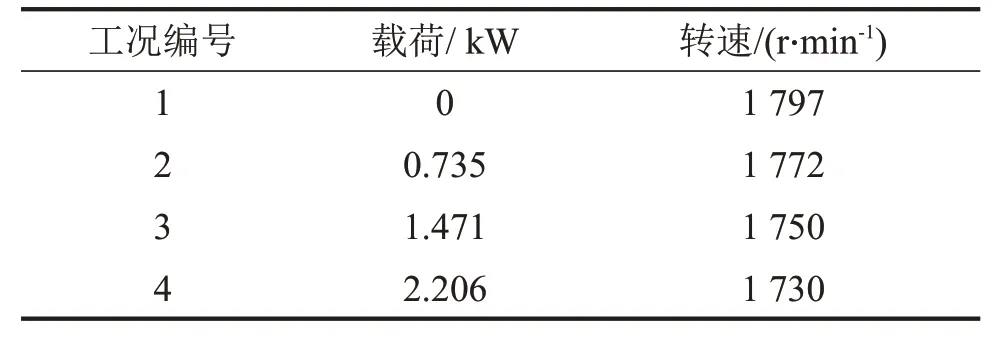
表2 实验工况参数

使用与仿真信号相同处理方法，分别计算不同轴承状态下4 种工况的双谱，结果表明不同工况下相同故障双谱相似度大。其中0.177 8 mm内圈故障在4种工况下的双谱如图5所示。

分别计算外圈故障、滚动体故障和正常状态双谱，结果表明不同轴承状态双谱差异性较大。其中工况1 情形下故障点直径为0.177 8 mm 的外圈故障、滚动体故障和正常状态双谱如图6所示。

图5、图6结果表明双谱能有效表征不同故障状态下的轴承振动特性。正常情形下，轴承不产生周期性冲击，双谱分布简洁，体现机械系统自身振动特性。滚动体出现故障时，缺陷部件在保持架束缚下周期性激励滚道，产生的双谱较正常情形时复杂。内圈出现故障时缺陷部位离传感器位置较远，冲击激励在传输过程中产生的振动较为复杂，对应的双谱比正常情形和滚动体出现故障时复杂。外圈出现故障时激励源离传感器最近，双谱幅值最大，双谱分布比正常状态复杂，但比滚动体及内圈出现故障时简洁。

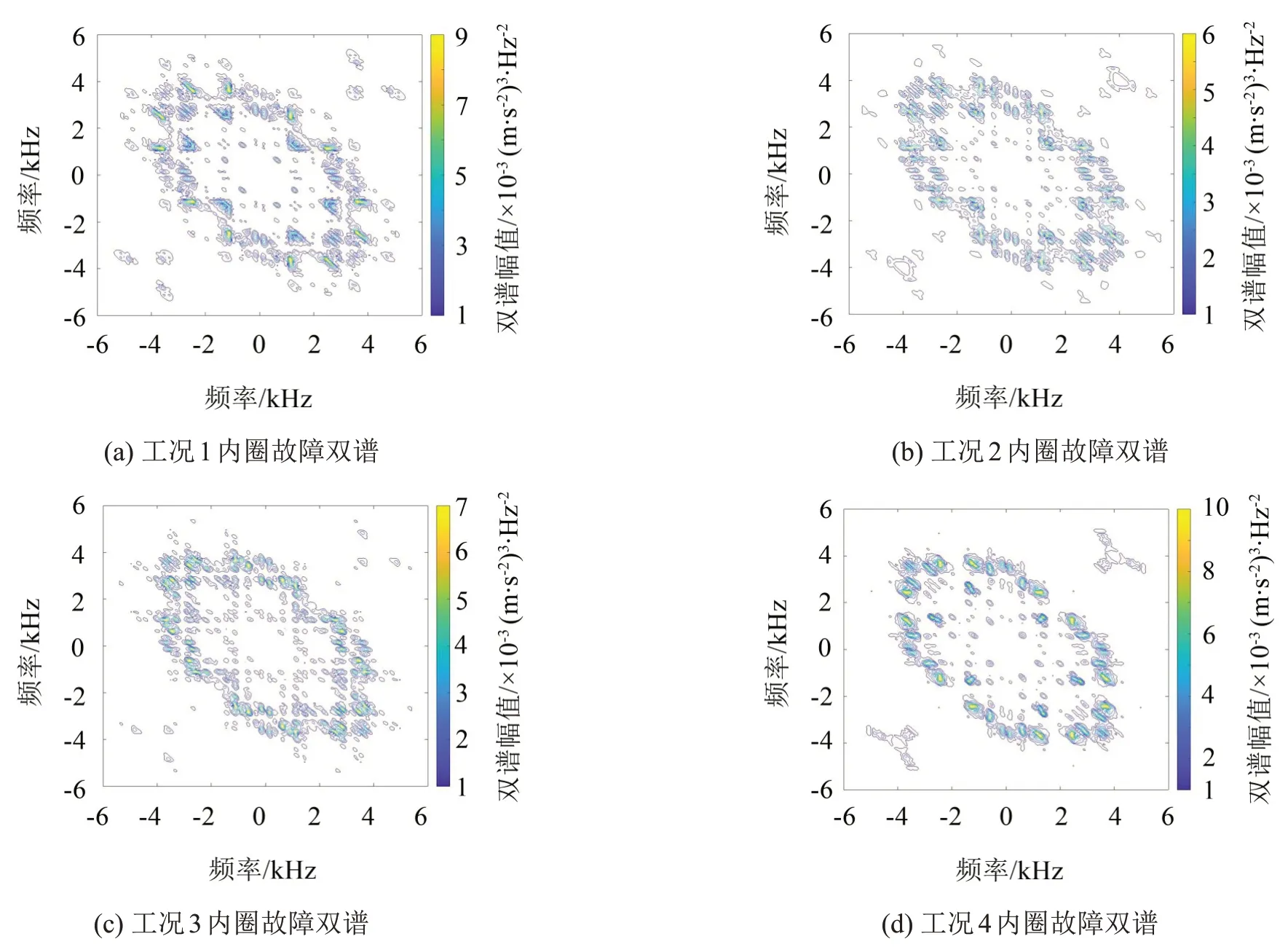
图5 变工况下内圈故障双谱

图6 不同故障类型双谱

对仿真和实测信号的分析结果表明，双谱在不同工况下具有较大相似性，在不同故障类型下具有较大差异性。因而可利用双谱对工况不敏感特性实现滚动轴承变工况故障诊断。

3.3 基于双谱和K近邻算法的变工况故障诊断

实验依故障程度不同分3 组进行，故障点直径分别为0.177 8 mm、0.355 6 mm 和0.533 4 mm。每组实验包含4种运行工况，参数如表2所示。双谱计算方法与验证仿真信号和实测信号时相同。

构建数据集时，K近邻算法中参数m在0.177 8 mm时取值为1，对于另外两种故障程度取值为3，近邻值K皆取5。实验时使用5折交叉验证法，结果以“均值±标准差”方式表征。在轻度故障(直径0.177 8 mm)时，对于任意一种工况的训练集，4 种工况下所有轴承状态的辩识精度皆为100%，结果不再列表描述。中度故障(直径0.355 6 mm)和重度故障(直径0.533 4 mm)时，各工况训练集的辩识精度如表3和表4 所示。表中第一列工况状态的“训练→辩识”，分别表示训练数据和辩识数据的工况编号。

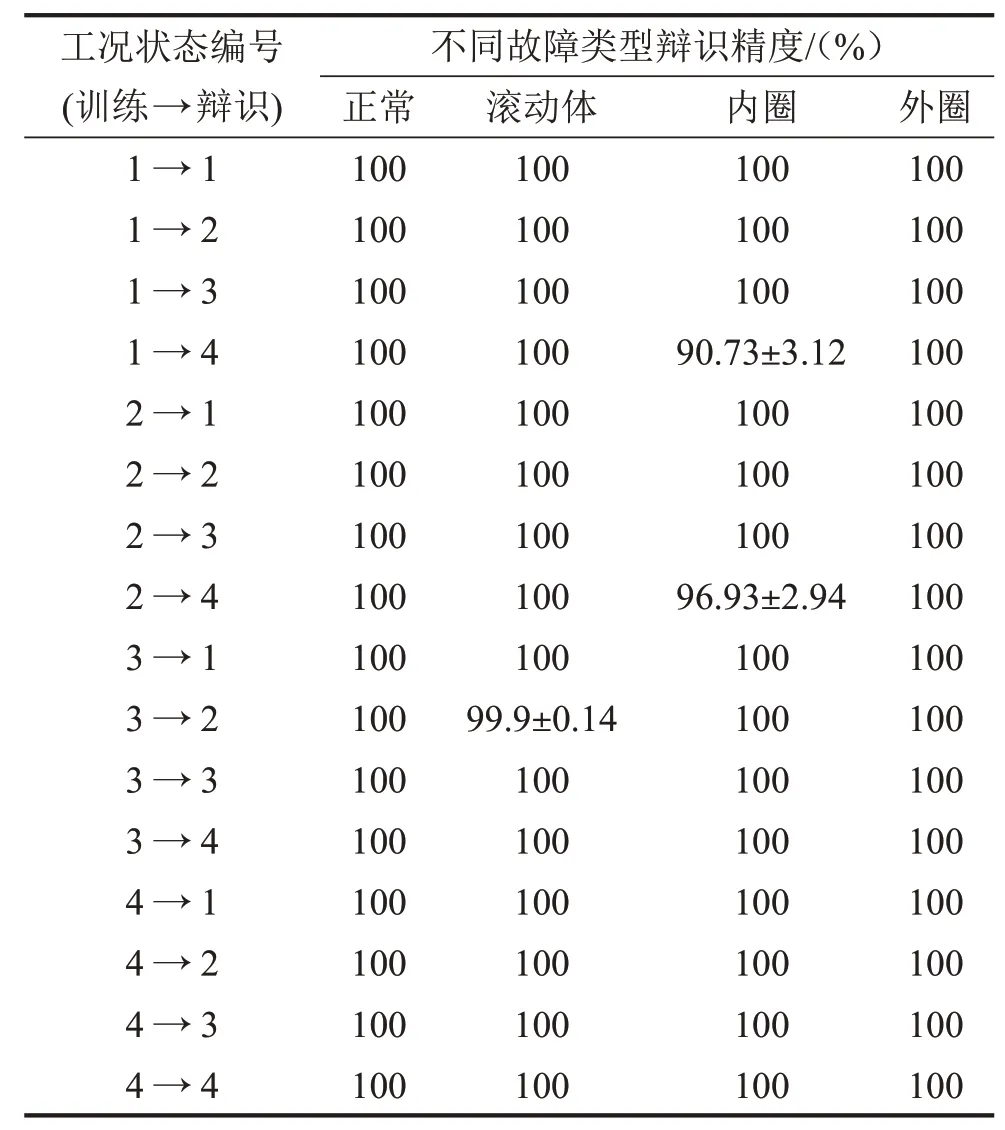
表3 变工况故障诊断辩识精度(故障点直径为0.355 6 mm)

表4 变工况故障诊断辩识精度(故障点直径为0.533 4 mm)

诊断结果表明，利用双谱对工况不敏感和对故障类型敏感特点，结合K近邻智能识别方法，对于3种故障程度皆实现4 种工况的轴承状态辩识，是一种有效的变工况故障诊断方法。

故障点直径为0.177 8 mm时的辩识精度优于另外两种程度故障，其原因是在早期故障阶段缺陷部位产生的冲击能量较小，激起的振动模态没有另外两种程度故障的复杂。而双谱又具有较强的高斯噪声抑制能力，从而可提取出更为稳定的特征参数，使诊断模型具有较高的辩识精度。

3.4 对比研究

为验证双谱分析方法优势，选择6 种对工况变化不敏感的时域无量纲参数[36]构建特征向量。它们分别为波形因子、峰值因子、脉冲因子、裕度因子、斜度因子和峭度因子。使用相同的训练、测试数据及辨识方法，其对于3 种故障程度辨识精度皆低于双谱分析方法。对于故障点直径为0.355 6 mm 的故障，使用工况1 数据训练模型，采用4 种工况数据进行测试的5 折交叉验证结果如图7 所示。其它3 种工况的训练模型以及其它两种故障程度下的诊断皆未取得可靠结果，因篇幅关系不再陈述。

图7 所示结果表明，时域无量纲参数虽然具有工况不敏感特点，但在时域提取数据时易受噪声干扰。未经预处理情况下进行变工况诊断，仅能有效识别部分故障，有些状态下辨识精度低，存在误判风险。而双谱能有效抑制高斯噪声，其具有对工况变化不敏感特点又能提取轴承系统的内在不变特征，进而可在无需信号预处理情形下实现可靠的变工况故障诊断。

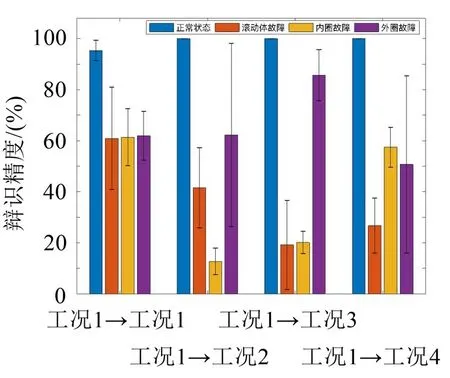
图7 对比实验辨识精度与标准差

4 结语

提出使用双谱分析提取对工况不敏感特征参数进行诊断方法，实现无需预处理环节的变工况故障诊断，得到下述结论：

(1)双谱分析方法直接提取对于工况变化不敏感的特征参数，无需额外的信号预处理或特征再处理环节，是一种简单易实施的变工况故障诊断手段。

(2)通过双谱分析可有效提取滚动轴承振动系统的内在不变特征。双谱分布受工况影响小，在不同工况下具有较大相似性，是一种有效的变工况特征参数。

(3)双谱分析能有效表征轴承振动特性。不同故障的双谱具有较大差异性，适合通过双谱分析进行智能故障识别。