基于优化VMD的车轴裂纹和车轮扁疤故障诊断

蒋宇涵，华春蓉，董大伟，熊丽波，王 瑞

（西南交通大学 机械工程学院，成都 610031）

车轴裂纹和车轮扁疤是列车轮对系统的常见故障，车轴裂纹通常是由于轮对长时间工作或存在材料缺陷所致，而车轮扁疤一般指由于列车制动、轮轨挤压所造成的轮面擦伤或剥离，两种故障均会引起轮对的异常振动，威胁行车安全[1-2]。因此实现对于运行中的轮对车轴裂纹和车轮扁疤的故障诊断，对保证列车的安全运行具有重要意义。

Rolek 等[1]采集了含裂纹轮对振动信号，使用快速傅里叶变换（Fast Fourier transform，FFT）得到信号谐波分量，诊断了车轴裂纹损伤程度。Gómez等[3]使用小波包变换分解并重构轮对振动信号，结合能量变化识别了车轴裂纹。张绪景[4]使用集合经验模态 分 解（Ensemble empirical mode decomposition，EEMD）对列车轮轨冲击信号进行分析，提取了车轮扁疤损伤特征。史红梅等[5]使用高阶谱分析轮对振动响应，定量识别了车轮扁疤损伤程度。

实际运行工况中的轮对振动信号受到轮轨随机激励、环境噪声等因素影响，具有非线性、非平稳特征，基于传统信号处理方法难以提取故障特征信息。在经验模态分解（Empirical mode decomposition，EMD）的基础上提出的变分模态分解（VMD）可将非平稳信号分解为不同时间尺度的平稳信号，且VMD鲁棒性较强，具有一定的抗噪及抗模态混叠能力。刘秀丽等[6]利用VMD 和小波分析提取了行星轮磨损故障信息。吴东升等[7]使用VMD 对轴承信号进行降噪，并通过KPCA 提取了故障特征信息。孟宗等[8]通过计算IMF 分量的能量占比确定VMD 分解个数，提取到轴承的微弱故障特征。焦博隆等[9]使用蝙蝠算法，以样本熵为指标对VMD的分解个数及分解中心频率进行优化，突出了转子裂纹的故障特征。吴守军等[10]利用波形法确定VMD 分解个数并对变速箱故障信号进行了预处理。胡爱军等[11]基于最大相关峭度获得VMD最佳分解中心频率，分离了轴承复合故障。

信息熵可直观反映信号故障状态，常被用来作为设备故障特征指标。吴守军等[10]将散布熵作为变速箱故障特征指标。艾延廷等[12]建立了融合熵距并对转子裂纹-碰摩耦合故障进行了诊断。李伟等[13]基于多尺度模糊熵诊断了齿轮箱故障。潘震等[14]以多尺度排列熵为特征值诊断了单向阀的故障。在样本熵的基础上提出的多尺度样本熵通过对数据进行粗粒化处理，改善了熵值仅在单一尺度上分析的局限性，从而可更准确地反映故障特征[15]。

车轴裂纹和车轮扁疤均会引起轮对动力学响应的周期性变化，且扁疤-裂纹耦合故障下的轮对动力学特征更加复杂。本文首先搭建考虑轮轨关系的轮对振动实验台，采集了不同状态下的轮对振动信号。再以样本熵、相关系数和均方误差为适应值进行VMD参数优化，并基于优化VMD提取了IMF1分量的多尺度样本熵-能量（MSEEN）故障特征指标。最后结合BP神经网络实现了轮对故障类型的诊断。

1 轮对振动响应分析

为模拟实际运行工况中的轮对故障，设计了考虑轮轨关系的轮对振动试验台，分别采集正常、扁疤故障、裂纹故障及扁疤-裂纹耦合故障下的轮对振动信号。

1.1 轮对振动实验台设计

搭建考虑轮轨作用的轮对振动实验台，为考虑轮轨关系同时控制实验装置大小，使用曲面轨道代替直轨道，如图1 所示。对轨道表面进行粗糙化处理，模拟实际工况中的轨道随机不平顺特征。

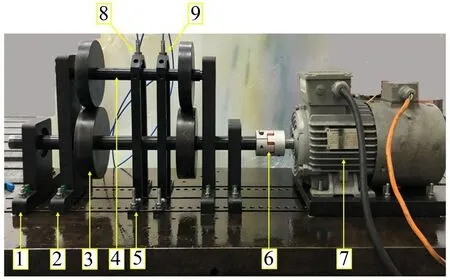
图1 轮对故障振动实验台

使用该实验台进行轮对系统正常、车轮扁疤、车轴裂纹和耦合故障工况下的振动响应测试。车轴裂纹深度为0.1d（d为车轴直径），通过线切割获得，车轮扁疤类型为轮面擦伤，如图2 所示。在建立耦合故障时，两者损伤程度不变。在轮对周围布置两个垂向的电涡流位移传感器。采样频率为5 000 Hz，采样时间为10 s，轮对转速为600 r/min。

图2 故障模拟

1.2 轮对故障振动信号分析

对不同轮对状态下传感器1测得的振动响应进行FFT分析，见图3。

由图3 可知，无论是车轴扁疤、车轮裂纹，还是二者的耦合故障，都会引起1X幅值增大。扁疤和裂纹故障还会引起2X、3X谐波成分，但仅根据频谱的谐波分量难以区分两种故障类型。由图3（d）可知，频谱中的2X、3X谐波成分被噪声或轮轨激励淹没。综上分析，基于FFT无法实现轮对车轴裂纹、车轮扁疤及耦合故障的诊断。

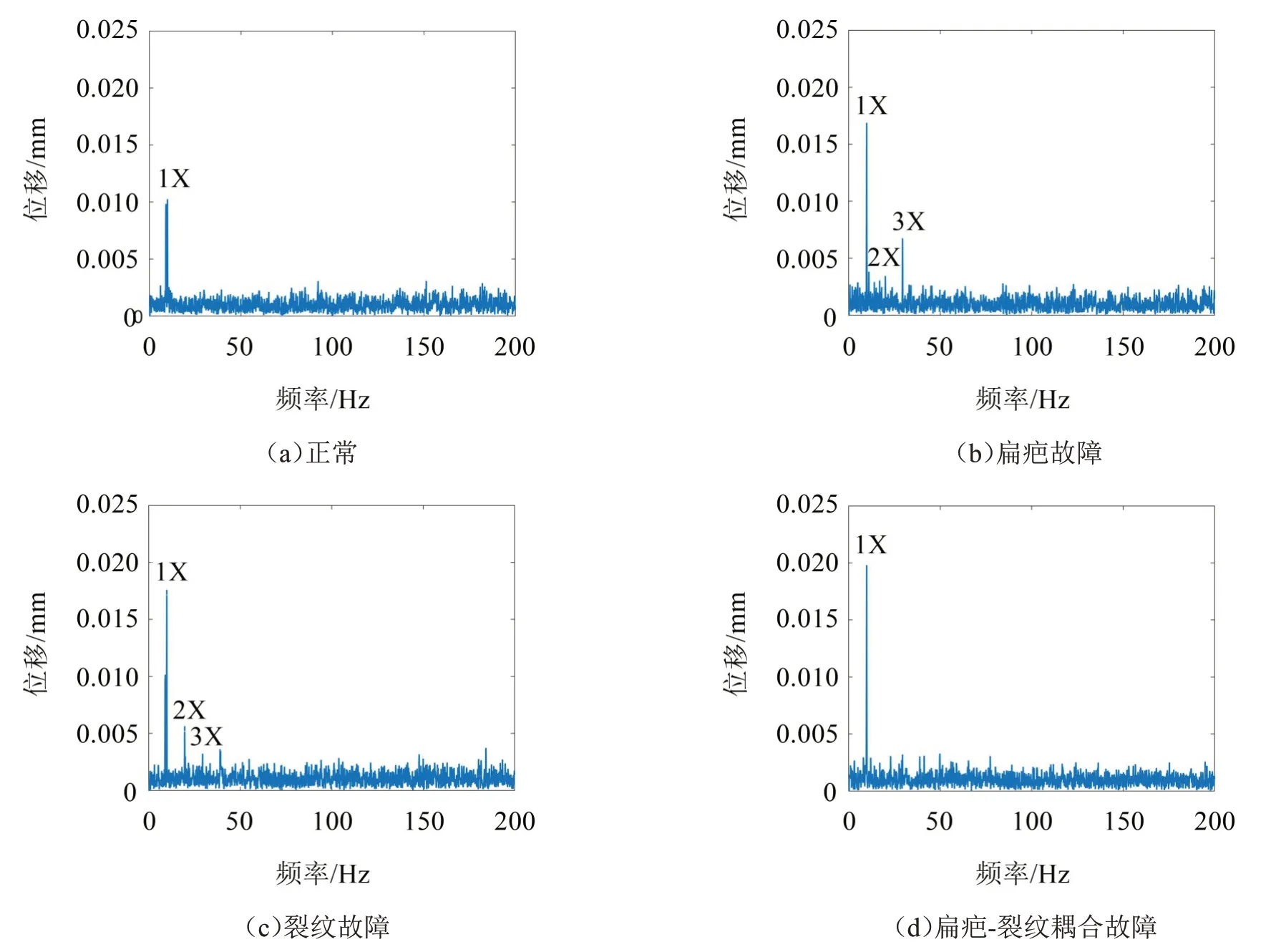
图3 不同轮对状态下的振动信号频谱图

2 VMD 的优化及MSEEN 特征指标构建

实际运行环境中采集到的轮对故障振动信号包含了轮轨激励和噪声等众多干扰因素，增大了故障特征提取的难度。VMD 虽具有一定的抗噪及抗模态混叠能力，但其分解个数K以及分解中心频率α的选择直接影响其分解和特征提取效果，且目前多采用经验取值或利用单个评价指标对VMD 分解参数进行优化[8-10]。为克服随机参数选取的不确定性，达到最佳VMD 分解效果，本文提出一种利用样本熵、相关系数和均方误差对VMD参数进行优化的方法，并在此基础上提取MSEEN故障特征指标。

2.1 VMD原理

VMD是一种信号分解估计方法，能够自适应地匹配最佳中心频率和有限带宽，实现信号的频域划分、固有模态分量的有效分离，从而得到信号的有效分解成分[16]。VMD关键在于构造和求解变分问题，其相应约束变分表达式为：

式中：K为基本模态分量个数分别对应第k个模态分量及其中心频率，∂t为解调信号梯度，δ(t)为狄拉克函数，*为卷积运算符，f为所有模态分量的合集。

引入二次惩罚因子和增广Lagrange 乘子λ(t)将上述约束性变分问题转化为非约束性变分问题，并求得约束变分模型的最优解。增广Lagrange表达式为：

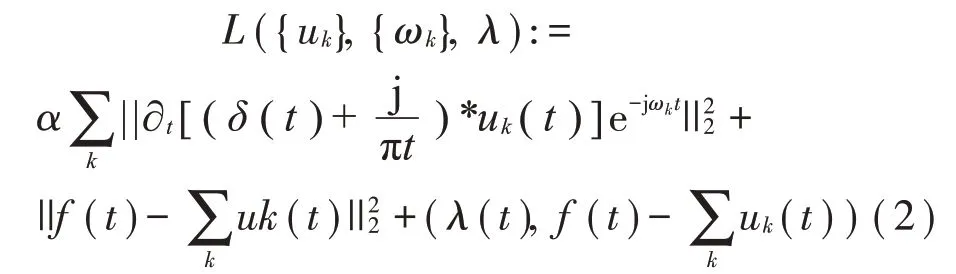
式中，||⋅||22为L2范数的平方。

使用乘法算子交替法求解式（2），得到估计固有模态函数和中心频率的更新算法为：

由VMD 原理可知，K和α的选取对非平稳信号的分解效果至关重要。

2.2 VMD的优化

引入遗传算法（Genetic Algorithm，GA）寻找最佳K值及α值，从而提升算法抗噪及抗模态混叠的能力。以待优化参数(K,α)为个体组成遗传算法的种群，计算种群中所有个体的适应值函数，适应度高的个体得以保留并增加其在下一代种群中的比重，通过不断迭代，得到最优个体。在VMD 参数优化中，可采用样本熵作为适应值对分解效果进行评价，IMF分量信息熵值越小，说明信号的稀疏性越好，分解参数更优[9]，时间序列xi的样本熵H为：

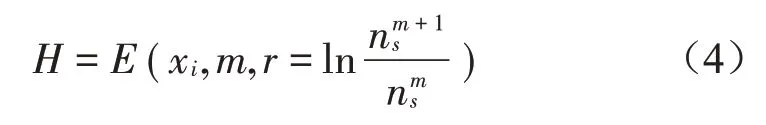
式中：m为嵌入矩阵维数，r为相似容限、分别为对时间序列插值化处理后的m行及m+1行向量。

为克服单一评价指标的不足，引入相关系数与均方误差，利用多个指标同时作为适应值从不同维度对参数优化效果进行评价。IMF分量间的相关系数ρui,ui+1的表达式如下：

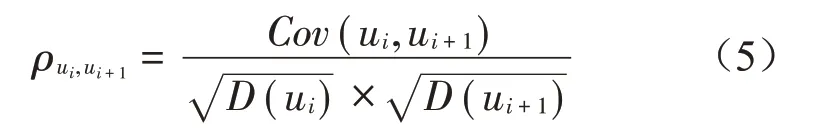
式中：ui和ui+1分别为根据VMD 分解得到的相邻的两个IMF 分量。相关系数越大，说明两者在相同频域区间的重叠部分越多，分解的效果越差，因此以IMF 分量间的相关系数作为适应值，能有效降低VMD 分解中频率混叠的概率。而针对实际轮对振动信号中的噪声干扰，采用均方误差M作为适应值来对VMD的降噪效果进行评估，见式（6）。

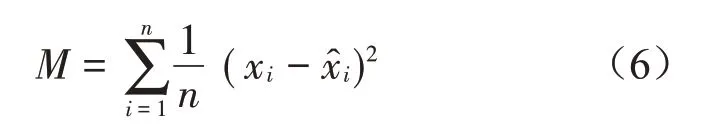
式中：xi、分别为原始数据和拟合数据。

综合考虑种群个体所对应的参数对样本熵、相关系数及均方误差的影响，构造适应度函数Z，见式（7）。通过GA 算法寻找最佳适应度函数值Z*，Z*所对应的个体即为最佳VMD分解个数K*及分解中心频率α*。

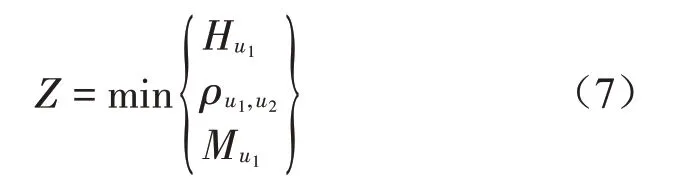
式中：Hu1为IMF1分量的样本熵值，ρu1,u2为IMF1和IMF2分量的相关系数，Mu1为IMF1分量的均方误差。

VMD参数优化的具体流程如图4所示。

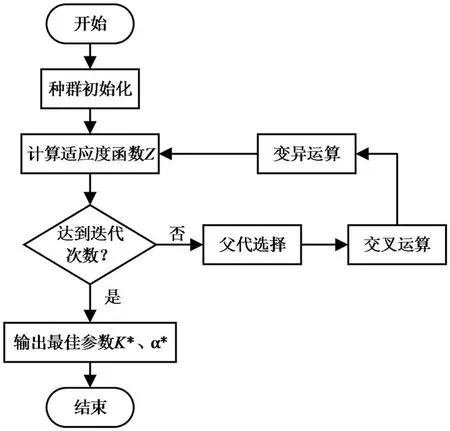
图4 VMD参数优化流程

2.3 MSEEN特征指标构建

多尺度样本熵（MSE）的计算分为两步，一是时间序列的粗粒化处理，以得到粗粒化序列，二是计算不同尺度因子下粗粒化序列的样本熵HMSE，如式（8）至式（9）所示：

式中：τ为时间尺度因子，xi为时间序列。

式中：m为嵌入矩阵维数，r为相似容限，nms、分别为粗粒化时间序列的m行及m+1行向量。

因多尺度样本熵对分布式故障的敏感性较低，故同时引入信号能量（EN）指标，时间序列xi的信号能量EEN的计算公式如下：

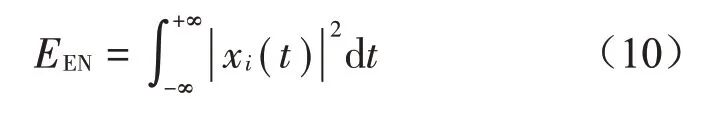
构建多尺度样本熵-能量指标XMSEEN作为轮对故障诊断特征向量，XMSEEN={x1、x2}，x1，x2分别为IMF1分量的多尺度样本熵HMSE和信号能量EEN。

3 轮对故障诊断

使用优化VMD分解轮对故障振动信号，提取正常、车轮扁疤、车轴裂纹及扁疤-裂纹耦合故障下IMF1分量的MSEEN 特征向量，并结合BP 神经网络诊断故障类型。

3.1 优化VMD分解

图5 为采用VMD 和优化VMD 分解轮对扁疤-裂纹耦合故障振动信号所得到的前3 个IMF 分量。表1 比较了IMF 分量的样本熵值、分量间相关系数以及均方误差。

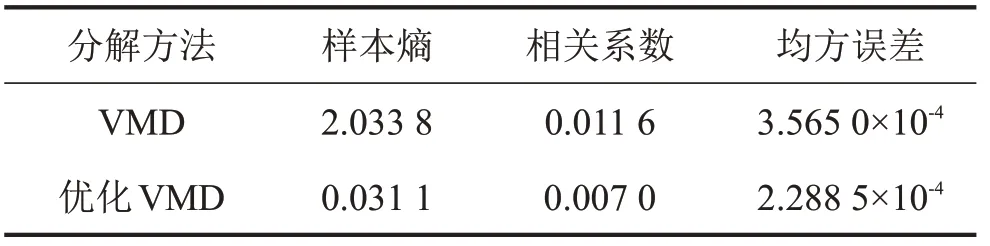
表1 适应值对比

由图5 和表1 可知，在扁疤-裂纹耦合故障情形中，基于VMD 分解得到的IMF 分量稀疏性较差，相邻分量的相关系数较大，且IMF1～IMF3的频谱在低频区间出现了一定程度的混叠。而优化VMD 分解后的IMF分量稀疏性更好，在IMF1分量中保留了轮对信号1X、2X 特征成分，且均方误差值小，降噪效果更佳；此外，从IMF1时域图中可观察到扁疤故障引起的冲击特征。因此采用优化VMD 能从原始轮对信号中提取故障特征信息，并有效避免模态混叠，同时具有更好的降噪效果。

图5 基本模式分量时频域图

3.2 故障指标提取

结合式（8）至式（10）提取正常、扁疤故障、裂纹故障及扁疤-裂纹耦合故障下的轮对故障特征指标XMSEEN，针对每种轮对状态分别建立30组特征指标向量，表2为部分MSEEN特征指标向量。

表2 轮对MSEEN故障特征指标

3.3 故障诊断

轮对故障类型表示为向量Y，Y={y1,y2}，见表3。将故障特征向量XMSEEN作为输入，故障类型Y作为输出，总样本数为120 组，取70%总样本对BP 神经网络进行训练，设置神经网络学习速率为0.1，误差目标值为0.000 01，最大迭代次数为1 000，利用剩余样本进行测试。

表3 神经网络故障类型输出

为验证本文优化VMD-MSEEN方法的有效性，将其与VMD-MSEEN 和EMD-MSEEN 方法的诊断结果进行对比，部分测试输出及期望输出见表4，不同方法的故障诊断识别率对比如图6所示。

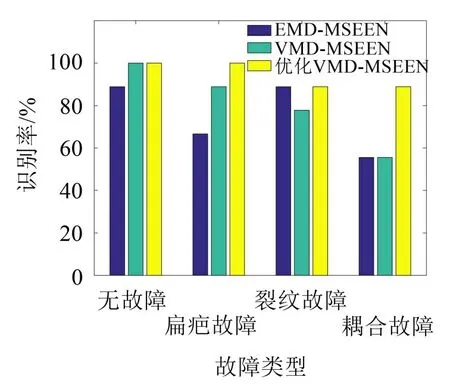
图6 不同方法故障识别率

由表4 和图6 可知，基于优化VMD-MSEEN 方法的BP神经网络预测输出更接近期望输出，可完全识别轮对的正常情形和扁疤故障情形，对裂纹故障及扁疤-裂纹耦合故障的识别率均达到了88.89%，高于其他两种组合诊断方法。此外，基于优化VMD-MSEEN 方法的轮对扁疤-裂纹耦合故障识别率比另外两种方法均高33.33%。

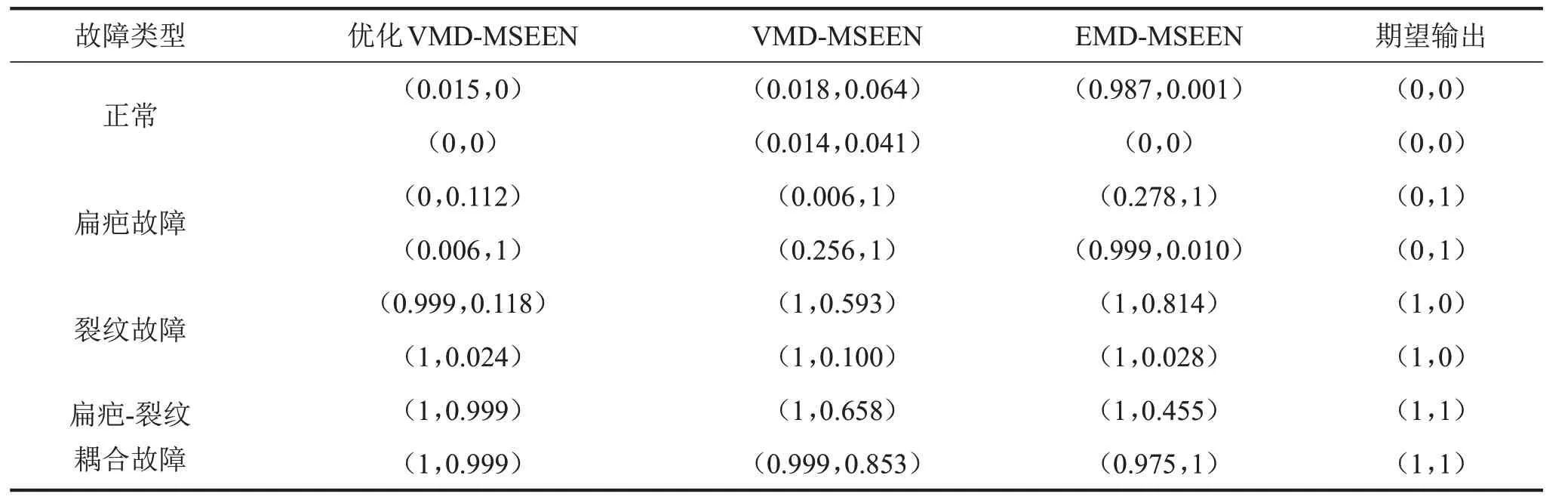
表4 不同故障诊断方法对应的BP神经网络输出

通过统计3种方法识别不同轮对故障状态的总体表现，EMD-MSEEN、VMD-MSEEN、优化VMDMSEEN的轮对状态总识别率分别为75%、80.56%、94.44 %，验证了本文提出的优化VMD-MSEEN 方法的有效性。但在实际运行工况中，轮对信号信噪比较低、样本量不够等情况可能对故障识别率造成影响，因此还需进一步研究该方法用于实际工况的轮对故障诊断效果。

4 结语

（1）搭建了考虑轮轨关系的轮对振动测试实验台，测试了轮对在正常、车轮扁疤、车轴裂纹及扁疤-裂纹耦合故障下的振动响应。

（2）以样本熵、相关系数和均方误差为适应值，使用遗传算法对VMD 进行优化，并基于优化VMD得到轮对故障信号IMF 分量。优化VMD 有效降低了分量间的模态混叠，使分量稀疏性更好，同时更突出轮对信号的故障特征信息。

（3）提出了一种多尺度样本熵-能量的故障特征指标，并结合BP 神经网络进行了车轮扁疤、车轴裂纹及耦合故障的诊断，总识别率达到94.44%。本文方法为实际运行工况中的轮对故障诊断提供了一种思路。