频率法索力测量误差分析及索力计算公式优化*
王建宇 杨建荣 曾章波 裴志勇
(1.昆明理工大学建筑工程学院 昆明 650500;2.中国电建集团华东勘测设计研究院有限公司 杭州 311122)
0 引言
随着科技水平的进步和建筑材料的不断发展,桥梁的形式变得多元化,拉索结构被广泛应用于桥梁当中,拉索作为重要的传力构件,索力的变化会影响全桥的内力变化,因此索力的精准识别变得十分重要。在桥梁的施工阶段、使用阶段都需要对索力进行精准控制,因此高效精准的测量成为急需解决的任务。在国内外学者的共同努力下,索力测量朝着多元化发展,并形成了相对完备的测试理论。索力测量的方法可分为直接测量法,如:压力传感器法、千斤顶张拉法;间接测量法,如磁通量法、垂度法、频率法等[1]。
采用直接测量法测得的数据更加精准,但使用时必须提前安装传感器,由此导致使用范围受限,且因传感器不可重复使用而导致造价偏高;间接法中的磁通量法和频率法应用比较广泛,磁通量法测量精度高、抗干扰能力强,但因成本较高在国内使用相对较少[2]。频率法测量因其操作方便、成本相对低廉、设备可以重复使用等优点,成为国内索力测量中最普遍的测量方法。
在现有的条件下,振动频率拾取的误差可以控制在万分之一以内,因此振动频率与索力对应关系的准确性,决定了频率法索力测量的精度。影响频率法测量精度的因素有拉索的计算长度、抗弯刚度、垂度以及边界条件等[3-4]。
国内外学者对影响频率法测量精度的因素进行了深入的研究,宋一凡等[5]对计算长度进行深入研究,给出了拉索有效计算长度的概念和有效计算长度的确定公式,但上述方法必须通过二阶固有频率来识别拉索的计算长度,具有一定的局限性;针对边界条件对频率法测试索力结果的影响,刘文峰等[6]通过能量法得到了简支边界条件和固结耦合边界条件下拉索索力测试的理论公式,使用该公式进行索力计算时需要准确识别前三阶自振频率,若某一阶频率识别不准确会使公式计算误差增大;孟少平等[7]用能量法推导出基于前两阶振动频率的计算公式,但两端简支的计算公式误差较大;李胡生等[8]通过对振动频率分解得到了新的索力与频率公式,但该公式使用时较为复杂不能简单快捷的求出索力;何雄君等[9]基于有限元软件等效出拉索计算长度并得出满足精度要求的计算公式,但是该公式使用时必须要预知成桥索力,对于投入使用多年的桥梁来说无法使用上述公式,使用范围受限。
上述计算公式部分存在缺陷,有的修正系数较多,使用时较为复杂,本文在假定简支边界条件下,首先分析影响索力与自振频率对应关系的因素中,哪种因素是误差产生的主要原因,然后从分析结果入手,结合实桥测试数据,对索力计算公式进行修正,得到一组实用简单、精度高的索力计算公式。
1 频率法测量索力
1.1 频率法测量索力原理
频率法测量索力时主要有两个关键步骤:①拾振器对频率的拾取;②通过频率与索力的对应关系求得索力。频率采集主要应用精密拾振器,测量拉索在激励条件下的振动信号、然后进行滤波、放大信号、频谱分析,最后根据频谱图来确定拉索的自振频率。由于拉索具有几何非线性,通过静力研究很难得出精确解,转而从拉索的动力特征入手,列出振动微分方程从而求解出振动频率与索力的对应关系[10]。
1.2 规范计算公式推导
基于弦振动理论在不考虑垂度的影响时,拉索的振动微分方程为[11]

(1)
式中,EI为拉索的抗弯刚度;E为弹性模量;I为截面惯性矩;T为索力;ρ为拉索的线密度;y(x,t)为拉索上各点随时间变化的位移函数。
求解式(1)可得拉索的振型方程为
Y(X)=Asin(αx)+Bcos(αx)+Csinh(βx)+Dcosh(βx)
(2)
其中,A、B 、C、D 为常数项,ω为固有频率。
(3)
(4)
(5)
(6)
当边界条件为简支时可以得到如下公式[12]:
(1)考虑抗弯刚度影响的公式
(7)
(2)不考虑抗弯刚度的影响公式
(8)
式中,T为索张力,N;ρ为 索的线密,kg/m;L为索的计算长度,m;fn为索第n阶自振频率,Hz;n为自振频率阶数。
2 误差分析及公式优化
影响索力计算公式精准度的因素有计算长度、抗弯刚度、垂度以及边界条件等,为得出上述哪种影响因素是误差产生的主要原因,本文以一座已经完成施工但尚未通车的系杆拱桥为研究对象,现场采集桥上吊杆索力数据,通过对索力测试数据的分析,确定出影响索力计算公式精准度的主要影响因素,并结合主要影响因素对公式进行优化。
2.1 工程概况
某下承式系杆拱桥,主跨跨径 145 m (计算跨径 141.34 m),桥宽22.8 m,包括1.95 m(吊杆区)+2.95 m (人行道)+13.0 m(车行道)+2.95 m(人行道)+1.95 m(吊杆区)。主跨上部构造为钢箱系杆拱,系杆箱长度 143.76 m,铅直面内矢跨比 1/6.09;拱轴线为抛物线,设有2片拱肋,每片拱肋有32根吊杆,全桥共计有64根吊杆,吊杆长度在5.587~24.131 m,其中1#—6#、26#—32#吊杆长度在5~15 m,7#—25#吊杆长度在15~25 m,大桥立面图见图1。

图1 大桥立面 (单位:m)
2.2 实桥索力测量
大桥施工安装吊杆时采用千斤顶进行张拉,为得到每根吊杆的精确索力,在千斤顶张拉完成时记录油压表的读数,从而得到每根吊杆的精确索力,下文将精确索力叫做成桥索力;在大桥尚未通车之前,采用频率法进行索力测量,记录每根吊杆的振动频率、自振频率阶数,使用式(7)、式(8)进行索力计算。将频率法测得的索力同成桥索力对比分析,就可以得出频率法的测量误差。给出上游几组具有代表性的测量数据于表1。
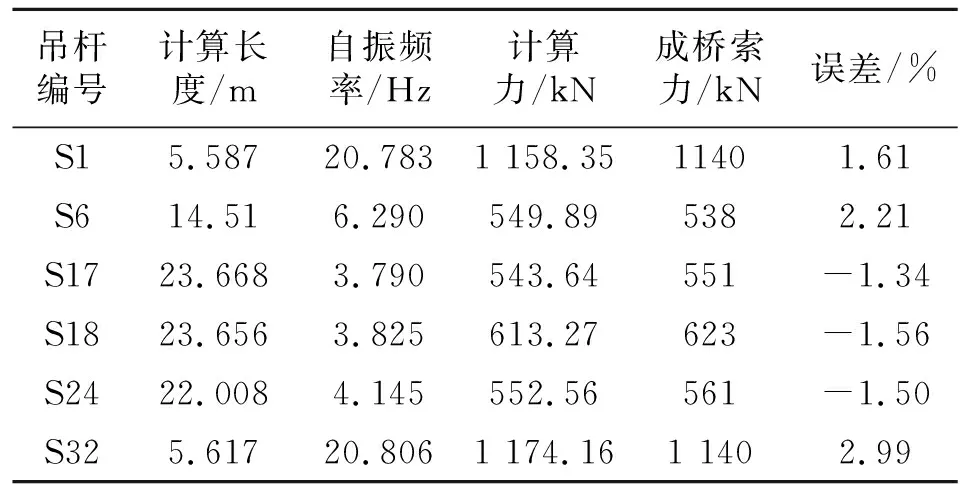
表1 索力测量数据
2.3 误差分析2.3.1 抗弯刚度对误差的影响
抗弯刚度是误差产生的原因之一,抗弯刚度往往会使振动频率增大从而导致测量结果偏大,减少抗弯刚度对振动频率的影响会使计算精度大大提高;某系杆拱桥吊杆长度在5.587 m到24.131 m之间,既包含短吊杆又包含长吊杆,为确定抗弯刚度对精准度的影响设置2种对比条件。条件①:使用式(7)进行索力计算,考虑抗弯刚度的影响;条件②:使用式(8)进行索力计算,不考虑抗弯刚度的影响。
定义抗弯刚度对误差的影响程度为B,计算公式为B=(W2-W1)/W2,式中W1为考虑抗弯刚度的误差,W1=(S1-S0)/S0,W2为不考虑抗弯刚度的误差,W2=(S2-S0)/S0,其中S1为条件①下的计算索力、S2为条件②下的计算索力、S0为成桥索力。将条件①、条件②的索力计算结果同成桥索力进行对比分析;给出上游几组具有代表性的数据见表2,因现场11#吊杆频率数据采集不准确,只对剩余31根吊杆进行分析,分析结果见图2、图3。
从表2中数据可以看出,计算索力时考虑抗弯刚度的影响会使计算索力整体减小,索力减小后同成桥索力对比发现,计算长度小于15 m的短吊杆误差减小,计算长度大于15 m 的长吊杆误差增大;图2为全桥上游31根吊杆在条件①和条件②下的误差曲线图,由图可知计入抗弯刚度的影响使短吊杆误差减小到0.85%,使长吊杆误差增大到-3.63%,故而计算索力时短吊杆必须计入抗弯刚度的影响;图3为抗弯刚度对误差的影响程度曲线图,从图中可以看出抗弯刚度对误差影响的程度在64.62%~-33.04%之间,从而得出抗弯刚度是误差产生的主要原因之一。

图2 条件①和条件②误差对比
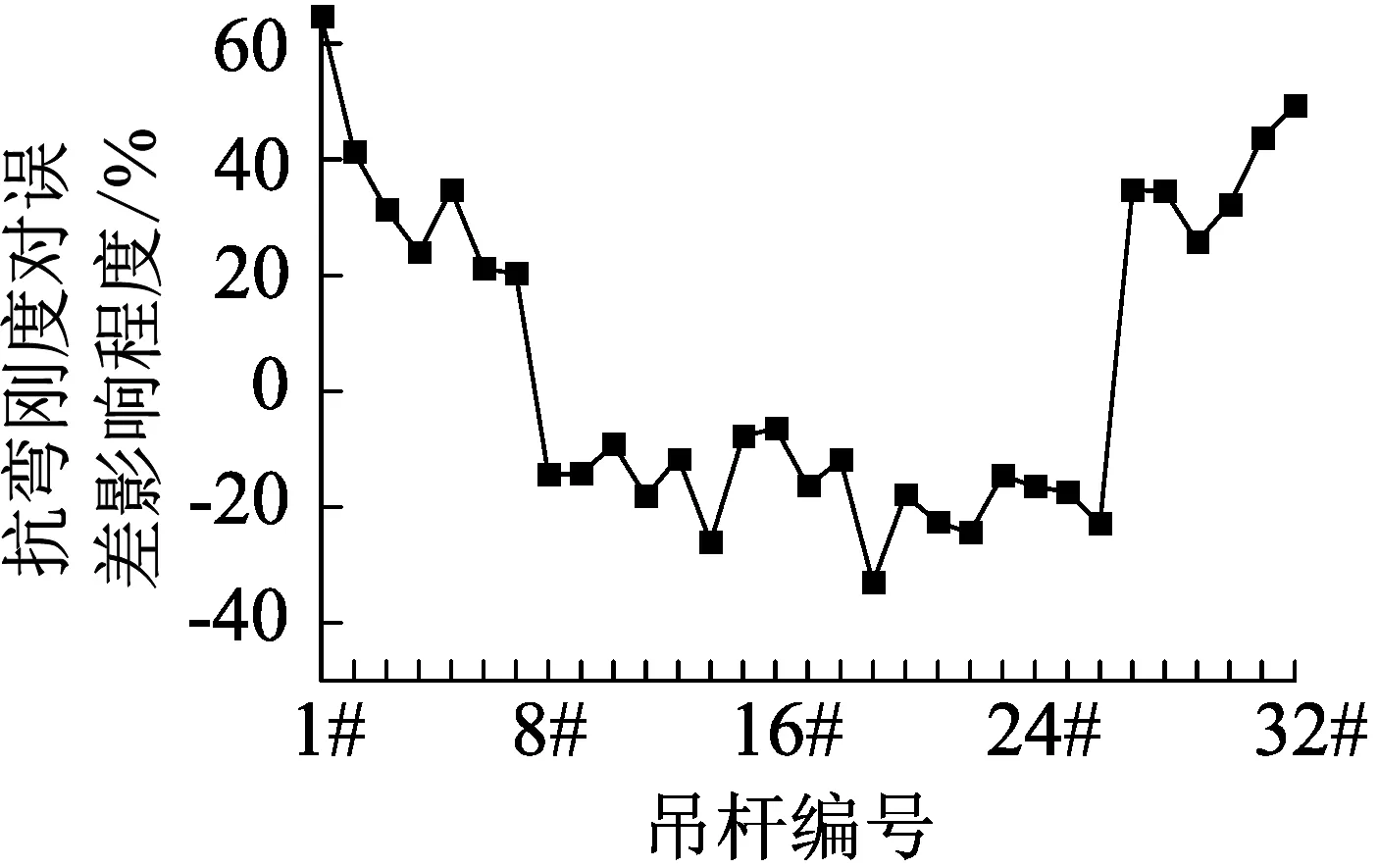
图3 不同吊杆抗弯刚度对误差的影响程度曲线
2.3.2 计算长度对误差的影响
计算长度是误差产生的原因之一,虽然目前索力测量时没有明确规定计算长度的取值,但多数情况下计算长度的选取,多选取两阻尼器前端或两锚头最前端之间的距离作为计算长度,这样选取可以达到取值方便和减少误差的目的。但按照上述方法取值会忽略吊杆在恒载作用下的长度增长值,本文通过实测数据分析恒载作用下吊杆长度增长值对计算索力的影响,现给出上游几组恒载作用下吊杆长度增长值的数据于表3。

表3 吊杆长度增长值数据
为得出吊杆长度增长值对误差的影响设置两种对比条件。条件③:使用公式(8)进行索力计算,考虑吊杆长度增长值的影响,计算长度取吊杆两锚头最前端之间的距离加上恒载作用下吊杆长度的增长值;条件④:使用公式(8)进行索力计算不考虑吊杆长度增长值的影响,计算长度只取吊杆两锚头最前端之间的距离。
定义计算长度对误差的影响程度为C,计算公式为C=(W4-W3)/W4,式中,W3为考虑吊杆长度增长值的误差,W3=(S3-S0)/S0,W4为不考虑吊杆长度增长值的误差,W4=(S4-S0)/S0,其中S3为条件③下的计算索力、S4为条件④下的计算索力、S0为成桥索力,将条件③、条件④的索力计算结果同成桥索力进行对比分析;给出上游几组具有代表性的数据见表4,详细分析结果见图4、图5。

表4 条件③、条件④的索力计算结果同成桥索力对比分析
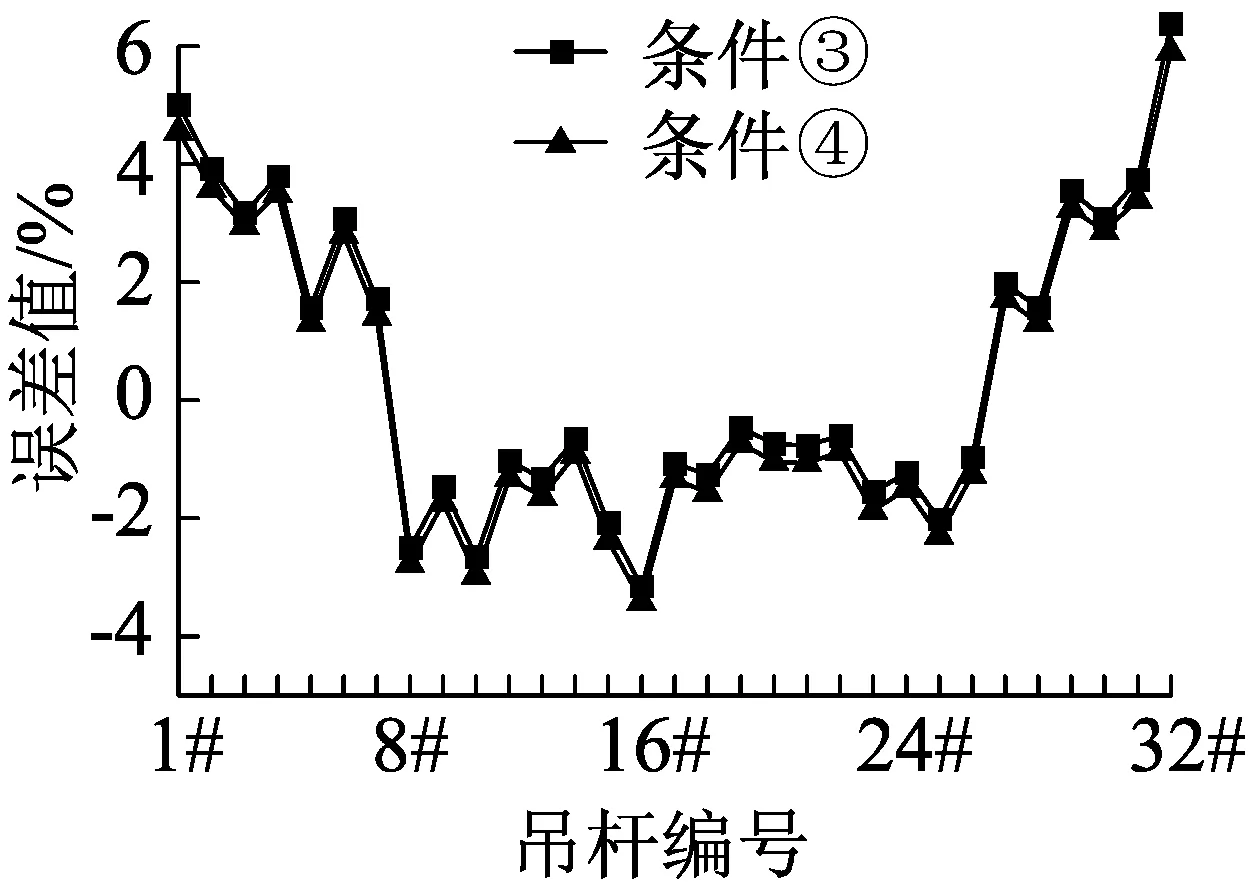
图4 条件③和条件④误差对比 图5 不同吊杆增长值对误差的影响程度
从表4中数据可以看出,计算索力时考虑吊杆长度增长值会使计算索力增大,索力增大后同成桥索力对比发现,短吊杆误差增大,长吊杆误差减小;图4为全桥上游31根吊杆在条件③和条件④下的误差曲线图,由图可知计入吊杆长度增长值的影响使短吊杆误差增大到6.37%,使长吊杆误差减小到-0.47%,故而计算索力时短吊杆不需要计入吊杆长度增长值的影响,而长吊杆必须计入吊杆长度增长值的影响;图5为吊杆长度增长值对误差的影响程度曲线图,从图中可以看出吊杆长度增长值对误差影响的程度在35.97%~-20.83%之间,从而得出吊杆长度增长值是误差产生的主要原因之一。
2.4 计算公式修正
引入修正系数A,采用origin软件编写拟合函数,对计算公式(8)进行修正,得出适合短吊杆的索力计算公式,拟合函数公式为:
(9)
将成桥索力,自振频率,计算长度带入上式,进行回归计算,经计算得出A=0.962,因此修正后的短吊杆计算公式为:
(10)
综合考虑抗弯刚度、吊杆长度增长值影响的索力计算公式为:
(11)
式中,△L为恒载作用下吊杆长度增长值。
2.5 公式实用性验证
为验证公式的实用性,将同一数据分别代入规范式(7)、式(8)及修正公式(11),计算出索力,同成桥索力对比求出各自公式的误差,通过比对误差的大小来判别公式的实用性。公式计算误差见图6。

图6 规范公式和修正公式误差对比
从图6中可以看出本文修正公式的误差在±2%上下浮动,只有16#吊杆误差绝对值大于3%,其余误差均在±2%左右;规范公式误差波动较大,但误差均小于±4%。通过对比可知本文修正公式精度高于规范公式,且两种公式误差均小于±5%,满足施工验收标准的要求[12]。
3 结论
(1)抗弯刚度对误差的影响程度在64.62%~-33.04%之间,说明抗弯刚度是误差产生的主要原因之一,对于长度小于15 m的短吊杆计算索力时必须计入抗弯刚度的影响。
(2)吊杆长度增长值对索力测试误差的影响程度在35.97%~20.83%之间,从而得出吊杆长度增长值也是误差产生的主要原因之一,对于长度小于15 m的短吊杆计算索力时可以不计入吊杆长度增长值的影响,长度大于15 m的长吊计算索力时杆必须计入吊杆长度增长值的影响。
(3)本文修正的索力计算公式能够精准地计入抗弯刚度和计算长度对索力的影响,其索力计算结果误差在±3%以内,满足施工验收标准的要求。

