基于傅里叶级数展开的裂变位能曲面与碎片质量分布计算
宿 阳,刘丽乐,陈永静,葛智刚
(中国原子能科学研究院 核数据重点实验室,北京 102413)
自1938年原子核裂变现象被发现以来,原子核裂变理论研究一直是核物理研究的重要领域。正如1939年Meitner、Frisch、Bohr和Wheeler[1-2]的开创性文章中所讨论的,原子核裂变可定性看作是原子核形状从单一复合核演化到断裂成两个碎片的过程。目前原子核裂变研究在实验和理论两个方面有了长足的进步,但仍缺乏能对裂变过程严格和精确描写的理论。
裂变碎片质量分布是原子核裂变的重要观测量,人们发展了各种方法用于计算裂变碎片质量分布,如唯像方法[3-6],这种方法通常是基于已有的物理图像和基本概念,采用简化的理论公式并引入一些模型参数,根据实验数据拟合确定参数再现裂变产额实验数据或其他可观测量。唯像方法通常在确定其参数的核区和能区可再现实验数据,但外推到未知区域时有很大的不确定性。此外,唯像模型未考虑动力学效应,无法描述裂变动力学过程,不能加深人们对裂变过程的理解。
另一种是基于能量密度泛函理论的原子核裂变微观理论方法[7-8]。裂变微观理论从核子-核子有效相互作用出发,原则上无需自由参数,具有较好的自洽性和预言能力。裂变微观理论分绝热和非绝热两类,绝热的微观动力学理论研究首先需计算原子核位能曲面,在位能曲面基础上进行动力学计算给出裂变碎片分布;非绝热的裂变动力学研究不需计算位能曲面,但只适合研究裂变过程和单个裂变事件,只能给出碎片最可几分布。需要强调的是,微观理论方法需较大的计算机资源,非常耗时,目前也只对有限的偶偶核裂变系统进行研究。
基于宏观-微观模型的裂变理论是目前发展较成熟的一种计算裂变碎片分布量的方法,这种方法首先要给定原子核的形状,然后基于宏观-微观方法计算裂变位能曲面,在位能曲面基础上进行含时或不含时的动力学计算给出碎片质量分布。这种方法既考虑了裂变核的静态性质,如位能曲面,又考虑了裂变动力学效应,是理论基础较好又具有一定预言能力的方法。相对裂变唯像模型,宏观-微观模型具有一定的物理基础,相对微观理论模型,宏观-微观模型无需大的计算资源。因此,宏观-微观模型是近年来有望成为替代唯像模型进行裂变后数据计算和评价的工具,成为国际上裂变研究的热点。
宏观-微观模型方法的基础是裂变过程中原子核形状描述,给定原子核一个形状,求出与这个形状相关的势能,因此可把原子核裂变过程描述为原子核形状在势能面上的演化。各种宏观-微观模型方法的不同主要在于采用的核形状描述方法不同。如美国洛斯阿拉莫斯国家实验室的Nix、Möller、Randrup等采用连接二次曲面描述核形状[9-10],德国法兰克福大学Maruhn和Greiner提出双中心壳模型[11],中国原子能科学研究院Liu等、日本东京工业大学Chiba等采用双中心壳模型描述核形状[12-15]来研究裂变产物,北京大学樊铁栓课题组则采用广义Lawrence形状描述法[16-17]。近年来,波兰Pomorski等[18]发展了基于傅里叶级数展开的核形状描述方法,这种核形状描述方法优势在于用少量的形变参数就可描述原子核裂变过程中的各种形状,且计算速度快,无需迭代计算。
235U是最重要的燃料核,其中子诱发的裂变产额数据是核反应堆设计与运行维护、核装置设计与测试、军控核查等的重要数据,同时也是裂变物理研究的基础数据。本工作以中子诱发235U形成的复合核236U为例,对236U裂变过程进行研究,分析236U位能曲面随不同形变参数的变化,计算236U裂变碎片质量分布,分析模型参数以及核温度对碎片质量分布的影响。
1 傅里叶级数展开的核形状描述方法
用尽量少的形变参量精确描述原子核形状是一项艰巨的任务,特别是与裂变有关的核形状,人们发展了一些有效的核形状描述方法[9-11,16,18],本文采用文献[18]提出的傅里叶级数展开的核形状描述方法描述裂变过程中的核形状。图1示出了在拉长形变、质量不对称度以及颈部宽度3个自由度下从鞍点到断点过程中典型的原子核形状示意图。
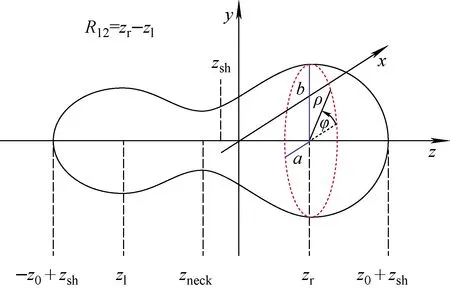
图1 柱坐标下原子核形状示意图Fig.1 Schematic visualization in cylindrical coordinates of nuclear shape
在柱坐标(ρ,z,φ)下,轴对称核形状方程可用傅里叶级数展开如下:
(1)
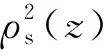
(2)
假定在给定的z处,原子核横向截面的形状(图1中红色虚线)用椭圆的形式来处理,a(z)和b(z)分别为椭圆的半短轴和半长轴,也可得到裂变过程中非轴对称的原子核形状,具体形式如下:
(3)

这种傅里叶级数表示的形状参量可将核形状展开到任意阶数,从而达到想要的精度。与常见的使用球谐函数描写的核形状相比,傅里叶形状参量能快速拟合核形状,在6阶内即可得到很好拟合结果,而球谐函数通常需展开到12阶以上。图2所示为使用傅里叶级数描述的核形状,傅里叶级数截断到6阶。
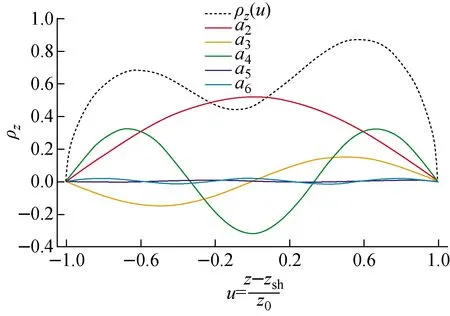
图2 傅里叶级数展开各阶系数对核形状的贡献Fig.2 Contribution of Fourier series coefficients to shape
虽然傅里叶级数展开系数an与核形状有直接联系,前3阶a2、a3、a4分别对应四极、八极和十六极形变,对裂变而言,这3种形变分别对应裂变核拉长量、质量不对称度和颈部宽度,但它们之间的对应关系较复杂。如式(2)中原子核拉长量c与展开系数中偶数项a2n的关系,首先,a2对c占主要影响,但c与所有的偶数项系数有关。其次,c与a2n呈负相关的关系。这导致通过系数a2直接反映拉长量时,对一些关键的裂变过程进行分析会变得复杂。因此,可用展开系数an组合1组新的集体坐标{qn}来表示形变参量,这样得到的集体形变参量可体现裂变过程的特征。新定义集体坐标{qn}如下:
(4)

表1 球形核对应的傅里叶级数展开系数(奇数项为零)Table 1 Values of Fourier expansion coefficients for spherical shape (Odd coefficients are zero)
集体坐标中,q2、q3和q4分别对应原子核拉长量、质量不对称度和颈部宽度。根据文献[19],q5和q6对小形变区液滴能的影响可忽略,在大形变区(剪裂线附近)也仅不超过0.5 MeV的影响。所以在之后的计算中不考虑q5和q6。上述集体坐标与原子核不对称形变自由度η一起构成了四维形变空间。
基于上述的核形状描述,采用宏观-微观方法计算裂变核的裂变位能曲面。对于一给定的形变的原子核,总能量Etot(η,q2,q3,q4)由式(5)计算。
Etot=Emac+Emic
(5)
其中,宏观能Emac通常在液滴模型框架内计算。文献[20]的Lublin-Strasbourg Drop (LSD)模型很好再现了原子核质量和裂变位垒高度,本文用LSD模型计算给出宏观能。微观修正能包括壳修正能和对修正能,分别采用标准的Strutinsky方法[21]和BCS方法[22]计算,其中用到的单粒子能级在给定形变参数(η,q2,q3,q4)下由Yukawa-Folded势进行计算。

Etot=Emac+Emicφ(T)
(6)
温度修正因子随温度的变化趋势如图3所示,当温度为0时,φ(T)接近1,当温度增大到3 MeV时,φ(T)接近0,说明此时微观修正能对位能曲面已无贡献,只剩下宏观能的贡献。
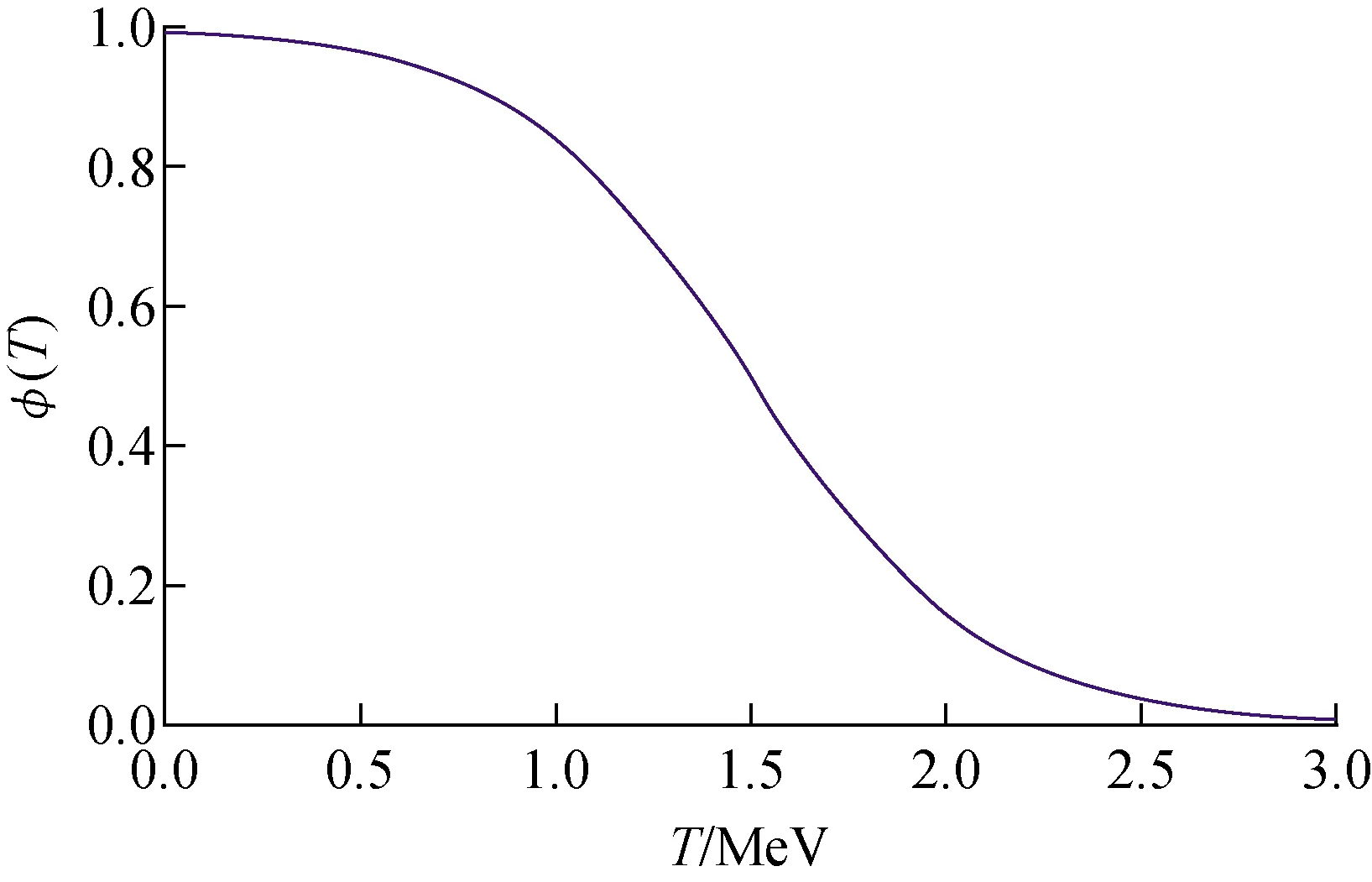
图3 温度函数φ(T)形式Fig.3 Form of temperature function φ(T)
2 集体模型描述裂变过程
裂变动力学过程的基本思想是原子核在裂变过程拉长方向(q2方向)的运动是相对缓慢的,同时伴随着垂直于裂变方向(q3,q4方向)上的快速振动,在Born-Oppenheimer近似(BOA)下(BOA近似认为当1个多自由度体系不同自由度的运动快慢相差悬殊时,可近似把这些自由度分开处理),总能量为E的裂变核体系波函数形式如下:
ΨnE(q2,q3,q4)=unE(q2)φn(q3,q4;q2)
(7)
其中:unE(q2)为裂变方向运动的本征函数,主要与原子核拉长形变q2有关,可通过WKB近似得到[24];φn(q3,q4;q2)模拟给定拉长形变q2后q3、q4方向上的n声子的快速集体振动。对于低能裂变的情况,在给定拉长形变q2时,(q3±dq3,q4±dq4)区域内的概率密度W(q3,q4;q2)可通过如下方式得到:
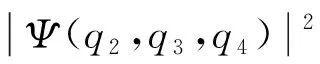
(8)
模型的进一步简化是使用下述形式的Wigner函数代替式(8)中概率密度。
(9)
其中:Vmin(q2)为给定拉长形变q2下最小的位能;T*为广义温度[25],考虑了裂变核的热激发和集体零点能E0。
T*=E0/tanh(E0/T)
(10)
质量数为A的原子核的温度T是通过唯像的关系(E*=aT2)从核的热激发能(E*)计算得到的,其中a=A/(10 MeV)。当T很小时,广义温度T*近似等于零点能;当T远大于E0时,T*近似等于T。零点能E0是本文动力学计算过程中的一个可调参量。
为得到给定拉长形变q2处的裂变碎片质量分布,需对概率密度W(q3,q4;q2)中的q4参量进行积分:
(11)
裂变概率很大程度上依赖于颈部的粗细,即颈部半径Rneck。假设颈部断裂概率P等于:
(12)
其中:Pneck为与颈部粗细呈正比的颈部断裂概率;k0/k为裂变方向较大的集体速度,在最终计算碎片质量分布时会直接消除。本文颈部断裂概率Pneck使用Gauss函数的形式来描述:
Pneck(Rneck)=exp[-lg 2(Rneck/d)2]
(13)
其中,d描述的是颈部断裂概率的半宽度,是本文动力学计算过程中的第2个可调参量。
引入颈部断裂概率Pneck(q3,q4;q2)后,概率密度分布(式(11))中对q4的积分可写为:
(14)
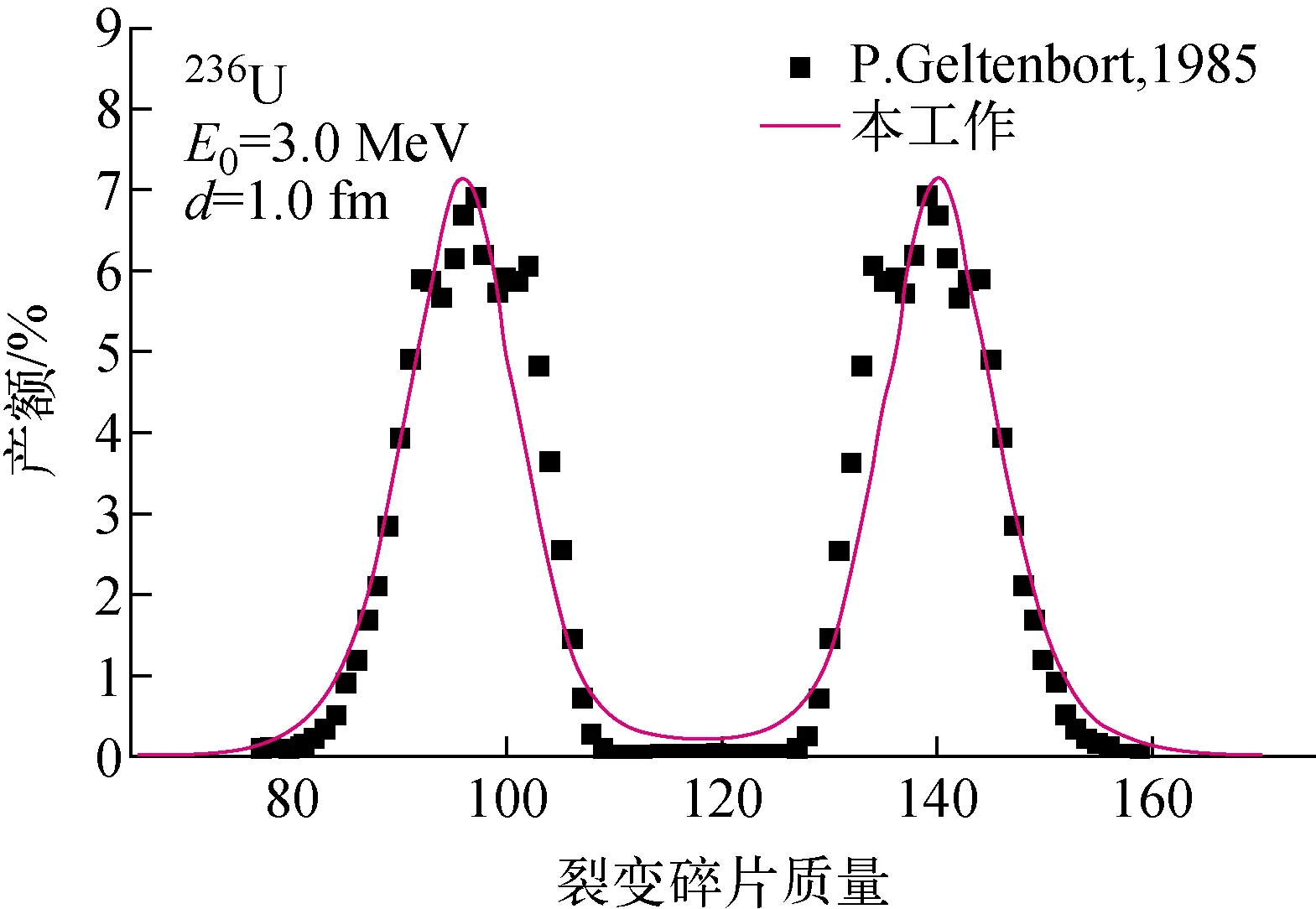
在上述近似中,对于一个给定的q3,裂变可能会以不同的概率发生在q2的一段区域内。若认为一部分原子核在q′2处发生裂变,则在下一步q2处就不能再考虑。因此,为得到在给定q2处真实的裂变概率密度w′(q3;q2),需排除q′2 (15) 对q2进行积分后再进行归一处理就得到裂变碎片质量分布: (16) 由于q3和质量不对称度存在一一对应的关系,由式(16)即可得到与实验数据可直接比较的裂变碎片质量分布。 基于LSD模型和Yukawa-Folded势的宏观-微观模型计算了n+235U形成的复合核236U在非轴对称形变、拉长、左右碎片质量不对称以及颈部宽度4个集体自由度下的裂变位能曲面。计算时形变参数空间(η,q2,q3,q4)网格点的取值如下: η=0.00(0.03)0.21 q2=-0.60(0.05)2.35 q3=0.00(0.03)0.21 q4=-0.21(0.03)0.21 (17) 基于上述形变参数网格点,由式(6)可计算不同温度下每个网格点上的原子核的势能。 图4 (q2,η)平面上236U位能曲面 (在q3、q4方向上能量取极小)Fig.4 Potential energy surface in (q2,η) plane for 236U (as obtain after minization with respect to q3 and q4) 图4为(q2,η)平面上236U位能曲面(零温),对应非对称裂变。可看出,从q2>0.1开始,η=0的方向,能量均是最小的,即不存在使能量减小的其他η。其次,η=0方向存在明显的内外垒结构,内垒位于0.5 图5示出了236U在颈部宽度q4取最小时位能曲面在(q2,q3)平面的投影。从图5可看出,236U具有双峰裂变位垒结构,即对称裂变内垒和不对称裂变外垒。基态位置处于q2=0.35、q3=0附近,随着原子核继续拉伸,在q2=0.6、q3=0附近出现第1个鞍点,为对称裂变内垒;越过内垒原子核继续拉伸在对称裂变方向出现第2个极小(图中b点),也即同质异能态;从第2极小出发,在非对称裂变方向q2=1.0、q3=0.09处出现第2个鞍点(图中c点),为不对称裂变外垒。可清楚看到,q3>0.06以后,在1.2 图5 236U在(q2,q3)平面的位能曲面Fig.5 Potential energy surface in (q2,q3) plane for 236U 更详细的位能曲面结果如图6所示,分别给出了不同拉长形变下的位能曲面分布图,从图可很清楚看出,在q2=1.05之前(图6a、b),(q3,q4)平面仅存在对称裂变方向上(q3=0)的1个能量最小点,对应图5中a、b两点的形状。当原子核继续拉伸到q2=1.05,即第2鞍点处,即图6c,原子核势能处于一较高水平,此时各种形状的核能量均较高,能量最低点出现在非对称裂变方向(图6c),说明了不对称裂变外垒存在的真实性(图5中c点)。越过外垒后原子核到达裂变谷所在的区域,从q2=1.2的位能曲面(图6d)可看出,由于对称裂变路径上较高外垒的存在,非对称裂变谷先于对称裂变谷出现(图5中d点),图6d中仅1个能量最小点,对应的左右不对称自由度q3=0.1,说明非对称裂变在两种裂变模式的竞争中处于领先位置。当q2=1.6时(图6e),从图6e可看出,对称裂变谷已出现,即图6e中的g点,对应的q3=0,而非对称裂变谷(q3=0.1)的深度更深。随着原子核继续拉长,在q2=2.0后,非对称裂变谷较对称裂变谷深得多,说明在236U低能裂变过程中,非对称裂变在裂变过程中拥有优势,这与前面的位能曲面分析以及碎片质量分布的实验结果一致。从图6a到图6f位能曲面的变化可看出,原子核从最初的1条裂变路径演化为2条裂变路径的过程中颈部自由度q4的演化起重要作用。 图6 给定q2值的(q3,q4)平面的位能曲面Fig.6 (q3,q4) potential energy surfaces for selected values of q2 图7为考虑了温度对微观修正能的影响后,计算得到的不同温度236U位能曲面在(q2,q3)平面上的投影。从图7可看出,随着温度升高,位能曲面对称裂变路径上的内垒(q2=0.6,q3=0)以及外垒(q2=1.2,q3=0)的高度均降低。其次,可看出,随着温度的升高,位能曲面的结构发生明显的变化,这是因为微观修正能的影响随温度增加而减弱。当温度T为2.0 MeV时,可清楚看出位能曲面趋近于仅宏观能的贡献(等势面比较规则)。从图中还可看出,随着温度的升高,q3约为0.10对应的非对称裂变道逐渐消失,到T=2.0 MeV只存在对称裂变道(q3=0)。 基于前面计算的位能曲面和第2章介绍的计算裂变碎片质量分布的简单集体模型,本文计算了零温236U裂变碎片质量分布(放中子前),并与热中子诱发235U裂变碎片质量分布进行了比较,如图8所示,计算中用到的两个参数E0和d分别取3.0 MeV和1.0 fm。可看出,理论计算结果与实验[27]符合较好,特别是轻重碎片质量分布的峰位。 图7 不同温度下(q2,q3)平面上236U位能曲面Fig.7 Potential energy surface in (q2,q3) plane for 236U with different temperatures 图8 236U裂变碎片质量分布计算结果 以及与实验值比较Fig.8 Fission fragment mass distribution of 236U and compared with experiment data 计算裂变碎片分布量的模型中有两个可调参数E0(零点能修正)和颈部断裂几率中出现的半宽度参数d。图9给出了不同E0(图9a)和d(图9b)的碎片质量分布计算结果。可看出,E0主要影响裂变碎片分布的宽度,随着E0的增大,碎片分布宽度也在增大,由于归一的影响,分布宽度的变化影响了峰的高度。而与颈部断裂相关的参数d对碎片质量分布峰位以及对称裂变和不对称裂变产额的贡献均有轻微影响。随着d的增加,重峰的峰位向碎片质量大的方向移动。需强调,低能裂变碎片质量分布的主要特征是由裂变核的位能曲面特征决定的。 图9 236U裂变碎片质量分布计算结果 随E0和d的变化Fig.9 Fragment mass distribution of 236U for different values of E0 and d 图10示出了不同温度236U裂变碎片质量分布计算结果。从图10可看出,随着温度的增加,236U裂变碎片质量分布的不对称裂变模式贡献逐渐降低,对称裂变模式贡献逐渐增加。这一结果与图7中位能曲面随温度变化趋势一致。图7中温度为2.0 MeV时,计算的位能曲面中非对称裂变道已消失,与此处温度为2.0 MeV时裂变碎片质量分布主要呈对称裂变模式一致。 图10 不同温度情况下236U裂变碎片质量分布Fig.10 Fragment mass distribution of 236U with different temperatures 基于傅里叶展开级数的核形状描述方法结合宏观(Lublin-Strasbourg-Drop)-微观(Yukawa-Folded)模型计算了中子诱发235U的复合核236U在拉长形变、质量不对称度以及颈部宽度自由度下的裂变位能曲面,分析了裂变过程中236U位能曲面随不同集体自由度的变化特征。用基于Born-Oppenheimer近似的三维集体模型计算了236U裂变碎片质量分布,分析了两个主要参数零点能、颈部断裂概率半宽度对裂变碎片质量分布的影响,研究了温度效应对裂变位能曲面以及裂变碎片质量分布计算结果的影响。研究结果表明傅里叶展开级数可合理描述原子核从基态演化到断点的裂变过程中各种核形状,LSD模型计算的宏观能和基于Yukawa-Folded势给出的微观修正可清楚给出236U裂变位能曲面在裂变核演化过程中随不同集体自由度的变化特征。基于上述位能曲面的三维集体模型再现了236U裂变碎片质量分布的主要特征,不同温度裂变碎片质量分布随温度变化趋势的计算结果与位能曲面分析结果一致,并且与现有碎片质量分布实验测量结果的变化趋势相符。3 计算结果及其分析
3.1 各集体坐标下的位能曲面分析
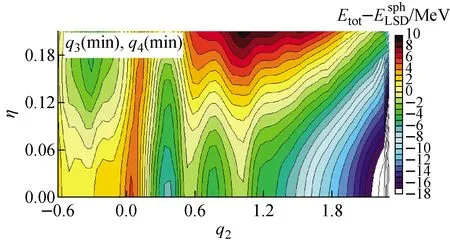
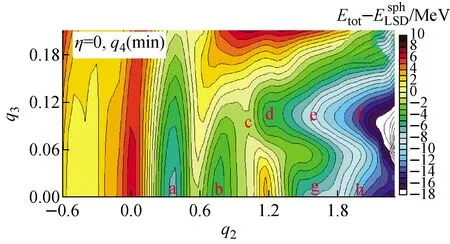

3.2 裂变产额计算结果分析

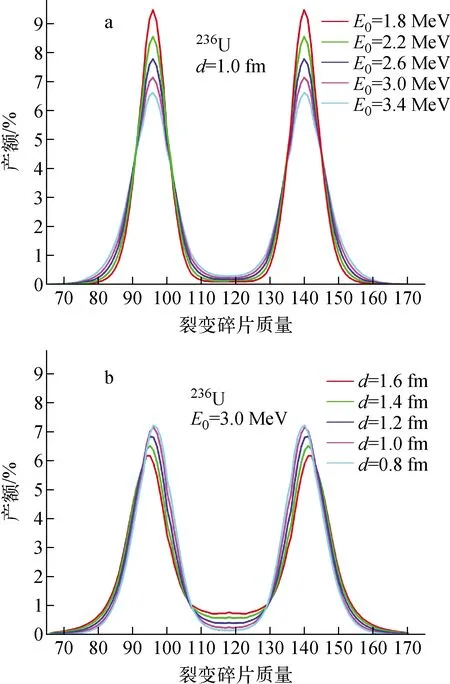

4 结论

