基于极端冲击的GARCH-MIDAS模型对股市波动率预测研究
张 莉,王 璐,计 玉,郝建阳
(西南交通大学 数学学院,四川 成都 611756)
金融资产收益率的波动在金融实践中扮演着重要角色,是现代金融理论的核心内容之一。股票作为金融市场的晴雨表,对风险管理、金融监管、投资组合决策以及金融衍生品定价等实务金融问题发挥着不可替代的作用,因此一直是学者研究的热点问题[1-2]。对股市波动率的研究最常使用的工具是GARCH模型[3]和一系列拓展的GARCH族模型[4]。GARCH族模型因能够较好地刻画股票收益的动态特征,如股市的波动聚集性、波动持续性和非对称效应等而被广泛使用。然而,GHYSELS等[5]研究表明GARCH族模型只能对同频数据建模。近几年,随着混频数据的可得性及混频数据在金融市场波动理论分析中的广泛使用,GARCH族模型对于股市中的数据建模显现出局限性。基于此,ENGLE等[6]将GARCH模型和MIDAS回归相结合提出了GARCH-MIDAS模型,该模型有优于GARCH族模型的表现,可将波动率分解为长期波动和短期波动两部分,其中长期项用于捕捉低频波动,短期项用于捕捉高频波动。GARCH-MIDAS模型在既没有忽略重要信息,又没有引入噪声的前提下,能够纳入不同频率的数据,减少因数据降频引起的信息丢失问题。
股票市场的波动存在多种特征,但GARCH-MIDAS模型对股票市场波动率特征的解释具有一定的缺陷。如金融危机、政治事件、自然灾难、局部战争等重大事件都会导致股票市场的剧烈波动,刘庆富等[7]研究表明一些重大风险事件无论在熊市还是牛市均对我国股市收益产生显著的影响;SCHWERT[8]研究表明1987年的股市崩盘和2007年的美国次贷危机都对股票收益产生巨大冲击;CHOUDHRY[9]也指出极端事件会造成股票收益率的结构性断裂,但GARCH-MIDAS模型是无法捕捉到股票市场中由极端事件引起的极端冲击。基于此,笔者对GARCH-MIDAS模型进行拓展使其包含极端因素,探究改进后的模型能否提高股票收益率的预测精度。
另外,股市中还存在非对称效应,但GARCH-MIDAS模型是无法捕捉到股市中的非对称效应的。因此,学者们不断对GARCH模型进行拓展,如ENGLE等[10]提出IGARCH模型来捕获股市中的波动持续性;NELSON[11]提出的EGARCH模型和GLOSTEN等[12]提出的GJR-GARCH模型都可以用来捕捉股市中的非对称性;MELE[13]研究发现非对称效应是影响股票价格波动的一个重要因素;PAN等[14]则指出包含非对称效应的GARCH类模型优于一般的GARCH族模型的预测性能。基于这一考虑,为研究非对称效应对股市波动率的影响,在包含极端因素的GARCH-MIDAS模型的基础上进行拓展,使其长期项和短期项均能捕捉到股市中的非对称效应。虽然WANG等[15]已经探究了包含极端冲击的GARCH-MIDAS模型对标准普尔500收益率的预测性能,但现有文献中同时考虑极端冲击和非对称效应对中国股市波动率影响的研究还较少。
基于上述分析,笔者拟完成以下工作:①在GARCH-MIDAS模型的长期项和短期项中加入极端冲击,且以超过某一临界值的门限值来定义股市中的极端冲击;②为使得包含极端因素的GARCH-MIDAS模型能够捕捉到股市中的非对称效应,对长期项和短期项分别进行改进。对于短期项,使用GJR-GARCH模型[16]代替GARCH模型;对于长期项,使用已实现半方差表示非对称效应;③为检验结果的稳健性,考虑极端事件的发生概率较小,探究不同门限值对拓展模型预测精度的影响。
1 GARCH-MIDAS模型及其拓展模型的构建
为充分利用高频数据中的丰富信息,提高计量模型估计的有效性和预测的精度,混频数据模型的使用越来越广泛,GARCH-MIDAS模型是混频数据模型中的一种,笔者基于GARCH-MIDAS模型进行拓展并研究其在中国股市波动率预测方面的性能。
1.1 GARCH-MIDAS模型
GARCH族模型只能处理同频数据,这对于混频数据的使用具有一定的限制。ENGLE等将GARCH模型和MIDAS回归相结合提出了GARCH-MIDAS模型,用以处理混频数据。具体形式如下:
(1)
εi,t|ψi-1,t~N(0,1)
(2)
(3)
式中:Ri,t为第t月第i天的对数收益率;Ei-1,t(Ri,t)为条件期望;ψi-1,t为在t月第i-1天时获得的信息集;Nt为第t月的交易天数;εi,t为随机扰动项,服从正态分布。假设Ei-1,t(Ri,t)=μ,则式(1)可进一步改写为:
(4)
(5)
其中,α>0,β>0,α+β<1。长期波动成分τt受已实现波动率RVt的影响,具体形式为:
(6)
(7)
式中:m为常数项;RVt为在第t月内的已实现波动率;k为滞后期数;K为RVt的最大滞后阶数,根据AIC和BIC信息准则,选取K=22;θ为滞后项RVt对长期项τt的整体影响,θ为正表示二者之间是正相关,为负表示是负相关;φk(ω1,ω2)为非线性的权重多项式函数,表示滞后k期的RVt所对应的权重。关于权重函数的选择,使用的是Beta多项式函数,具体形式为:
(8)
为保证滞后项权重呈衰减形式,即滞后期越大,对当前的影响越小,固定ω1=1,由系数ω2确定变量对长期成分的影响,简化后的Beta权重函数为:
(9)
考虑到历史数据对当前数据的影响呈衰减趋势,这里限制参数ω>1。式(1)~式(9)联合构成了标准GARCH-MIDAS模型,采用极大似然法估计模型的参数,待估参数为μ,α,β,m,θ,ω。
1.2 GARCH-MIDAS的拓展模型
1.2.1 引入极端冲击的GARCH-MIDAS模型(简记为EX-GARCH-MIDAS)
已有研究表明极端事件会导致股票市场的剧烈波动,且极端事件会使股票波动率发生结构性变化[17],因此研究极端事件对股市的影响具有重要意义。为使GARCH-MIDAS模型能够捕捉到股市中的极端冲击,对其进行拓展,并使用门限值来定义股市中的极端冲击,其中门限值可以通过经验分位数来确定[18]。基于此,改进后的短期成分gi,t的具体形式为:
gi,t=(1-α-β-I{Ri,t
(α+I{Ri,t
(10)
式中:α>0,β>0,α+β+I{Ri,t
为使长期项能够捕捉到极端冲击,受式(10)的启发,将已实现波动率分为3部分:负极端收益得到的已实现波动率、正极端收益得到的已实现波动率和正常收益得到的已实现波动率。拓展后的长期项τt的具体形式为:
(11)

1.2.2 引入非对称效应的GARCH-MIDAS模型(简记为AS-GARCH-MIDAS)
股票市场不仅受极端事件的影响,也存在非对称效应,对GARCH-MIDAS模型进行改进使其长期项和短期项均能捕捉到非对称效应。对于GARCH-MIDAS模型的短期项GARCH过程而言,由于ENGLE的研究结果表明GJR-GARCH模型比EGARCH模型在股票波动率上表现更好。因此,笔者使用GJR-GARCH代替GARCH(1,1)模型,即:
gi,t=(1-α-β-0.5γ)+
(12)
其中,γ为非对称杠杆系数。
为使长期项能够捕捉到股市中的非对称效应,将已实现波动率进行分解,用分解后的变量来捕捉由正收益率和负收益率引起的变化,采用已实现半方差来估计这种变化[19],其定义式为:
(13)
(14)
式中:N′为1个月的周期天数,令N′=22;RS+为正的已实现半方差,用来捕捉由正收益率引起的变化;RS-为负的已实现半方差,用来捕捉由负收益率引起的变化,该估计量提供了RV的完整分解,即RV=RS++RS-。拓展后的τt为:
(15)
由于式(13)和式(14)在任意范围内都是成立的,故式(15)能够捕捉到由非对称效应引起的变化。
1.2.3 引入极端冲击和非对称效应的GARCH-MIDAS模型(简记为AS-EX-GARCH-MIDAS)
对于同时包含极端冲击和非对称效应的GARCH-MIDAS模型的短期项,将式(10)和式(12)结合,拓展后的gi,t的具体形式为:
gi,t=(1-α-β-0.5I{Ri,t<0}γ--0.5I{Ri,t>0}γ+-
I{Ri,t
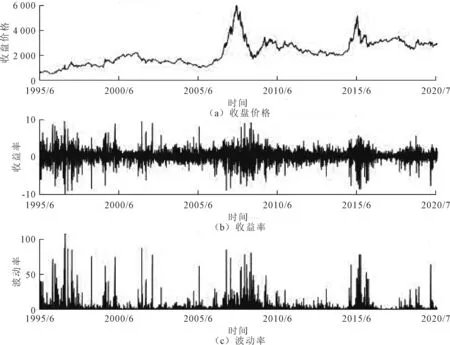
(α+I{Ri,t<0}γ-+I{Ri,t>0}γ++I{Ri,t (16) 式中:I{Ri,t (17) 上证综合指数(以下简称“上证综指”)是中国发布最早且最具代表性的指数,对其波动率研究具有一定的实际意义。中国股票市场作为一个新兴市场,考虑到该市场在1993年以前尚不规范且规模较小以及1995年5月的三日井喷行情,因此选择1995年6月1日—2020年7月1日的上证综指股票数据,共6 091个交易日,数据来源于国泰安数据库。股票收益率的具体计算公式为: Ri,t=100×ln(Pi,t/Pi-1,t) (18) 其中,Pi,t为第t月第i天的收盘价。上证综指时序图如图1所示,其中波动率用收益率的平方代替。全样本区间上的上证综指收益率的描述性统计如表1所示。 图1 上证综指时序图 表1 收益率的描述性统计量 由图1的收盘价格走势可以看出,2008年金融危机和2015年股灾阶段比其他样本期有更加剧烈的波动,2019年12月新冠肺炎的爆发也造成了股市价格的波动,这初步说明包含金融危机等在内的极端冲击会使中国股票市场的波动特征出现一些显著改变,故提出包含极端冲击的GARCH-MIDAS模型是非常有必要的,研究极端冲击对中国股市的影响是有实际意义的。 由表1可知,该收益率的平均值接近于零且方差远远大于均值;偏度小于零,说明该时间序列左偏,峰度大于3且J-B统计量显著,表明该时间序列不服从正态分布且表现出“尖峰厚尾”特征;ADF统计量在1%的水平下显著,表明该收益率序列是平稳的;Q统计量的结果表明在滞后5 d、10 d的时间范围内,都具有显著的自相关特征。因此,可以对该时间序列做进一步的分析和计量建模。 为探究在极端冲击中引入非对称效应的GARCH-MIDAS模型是否能够提高股票波动率的预测性能,首先将全样本数据划分为样本内数据和样本外数据,然后使用样本内数据对模型的参数进行估计。对于样本内和样本外数据容量的选择学术界还未有一致的结论,笔者选择5 091个数据作为样本内数据,剩余的数据作为样本外数据。因为极端事件发生的概率很小,选取的经验分位数为δ1=0.1,δ2=0.9,表示股市10%的极端负收益率或10%的极端正收益率。4个模型的总波动率和长期波动率走势图如图2所示,4个模型的参数估计结果如表2所示。 由表2可知,4类GARCH-MIDAS模型的参数估计几乎都显著,说明这4类模型均适用于中国股市波动率预测的研究。其中短期项中的参数α,β均显著,说明上证综指收益率在短期内具有强烈的波动聚集性,且α与β之和小于1且接近1,说明具有较强的波动持续性。4个模型的参数β都接近于1且在1%的水平下显著,这说明上证综指股票市场具有高度的波动性。从图2可以看出,长期波动率和总波动率走势一致,而且表2中参数θ均在1%的水平下显著,说明在上证综指股票市场中长期波动率主导着总波动率的变化。短期项和长期项中的非对称性参数均是显著的,说明在上证综指股票市场中存在明显的非对称效应,短期项中的非对称性参数γ显著大于零,表示在短期波动中“利空消息”对股票波动率的影响大于“利好消息”。对于长期项中非对称性参数θ+和θ-,模型不同符号不同,在AS-GARCH-MIDAS模型中,θ+显著为正、θ-显著为负,表示利空消息和利好消息均增加了股市的波动,不利于股票市场的长期稳定;在AS-EX-GARCH-MIDAS模型中,θ+显著为负、θ-显著为正,说明在极端冲击中考虑非对称效应时,负的收益和正的收益均会减小股市的波动,且θ->θ+,表明负的半方差对股票市场长期波动的影响大于正的半方差,即在长期波动中坏消息对股市的影响大于好消息。 表2 GARCH-MIDAS模型及其扩展模型的参数估计结果 同时,从表2还可以看出,极端冲击的参数均显著,说明中国股市会受到极端事件的影响。从EX-GARCH-MIDAS模型的参数估计结果可知,在短期项中,参数γ-*和γ+*均显著大于零,且γ-*>γ+*,说明负的极端冲击和正的极端冲击都会使股市的短期波动增大且极端负收益的影响大于极端正收益;在长期项中,参数θ-*>θ+*,且θ-*>0、θ+*<0,说明极端冲击会引起股市更大的长期波动,且极端负冲击的影响大于极端正冲击,这说明极端效应可能是引起股票波动持续性的一个重要根源。在AS-EX-GARCH-MIDAS模型中,参数γ-*>γ+*、θ-*>θ+*,说明在非对称效应下负极端冲击的影响大于正极端冲击;而且|γ+|<|γ+*|,|γ-|<|γ-*|,|θ+|<|θ+*|,说明在中国股票市场,极端冲击效应的影响要强于非对称效应。根据表2中的极大似然函数值判断出AS-EX-GARCH-MIDAS模型的预测性能表现最好。 判断一个波动率模型的优劣不是看其对样本内数据拟合的好坏,而是看其对样本外数据的预测能力[20],故笔者使用上述4类模型对上证综指进行样本外预测。由于静态数据预测波动率的方法没有考虑到远端数据和近端数据对预测模型的不同影响,因此采用滚动窗口预测,选取的滚动窗口长度H=5 091,每个模型获得M=1 000个未来一天的波动率预测值。 为判断模型的预测性能,采用HANSEN等[21]提出的模型信度检验法(MCS检验)。该检验相比于SPA检验不需要事先选择一个基础模型,是在模型集合M0(M0=4)中进行一系列的显著性检验,剔除M0中预测性能较差的模型,且允许最优模型的个数多于一个。该检验的零假设为: H0E(di,pq,t)=0 ∀p,q∈M0,p,q=1,2,3,4 H0表示两模型具有等效的预测能力,其中,dm,pq,t=Lm,p,t-Lm,q,t,Lm,n,t为根据第m个损失函数计算出来的第n模型的损失误差,其中m=1,2,3,4,5,n=1,2,3,4,t=H+1,H+2,…,H+M。选取5个损失函数作为判断预测误差的基准,分别为均方误差(MSE)、平均绝对值误差(MAE)、异方差调整均方误(HMSE)、异方差调整绝对值误(HMAE)、高斯极大似然损失函数误差(QLIKE),具体形式为: (19) (20) (21) (22) (23) 各波动率模型样本外预测的MCS检验结果如表3所示,可以看出所有波动率模型统计量p值几乎都大于0.25,说明GARCH-MIDAS及其拓展模型在上证综指股市预测性能方面表现不错。在MSE和MAE损失函数条件下,4类模型均通过MCS检验且AS-EX-GARCH-MIDAS表现最优;在HMSE和HMAE损失函数条件下只有AS-EX-GARCH-MIDAS模型通过检验;在QLIKE损失函数条件下,除GARCH-MIDAS模型外其他3类模型均通过MCS检验,且AS-EX-GARCH-MIDAS表现最优,这说明在GARCH-MIDAS模型中引入极端冲击和非对称效应能够提高模型的预测精度。 表3 GARCH-MIDAS模型及其拓展模型的MCS检验结果(样本外预测长度为1 000天) 2.4.1 不同的门限值 由表3可知,在波动率模型中考虑极端冲击和非对称效应能够提高模型的预测精度,为检验结果的稳健性,通过改变门限来检验模型。笔者给出了阈值为δ1=0.05、δ2=0.95和δ1=0.01、δ2=0.99两种情况的MCS检验结果,如表4和表5所示,该结果与表3结果一致,AS-EX-GARCH-MIDAS模型仍然表现出最好的预测性能。 表4 GARCH-MIDAS模型及其拓展模型的MCS检验结果(δ1=0.05、δ2=0.95) 表5 GARCH-MIDAS模型及其拓展模型的MCS检验结果(δ1=0.01、δ2=0.99) 2.4.2 AS-EX-GARCH-MIDAS模型和GARCH模型样本外预测比较 通过MCS检验探究GARCH、GARCH-MIDAS和AS-EX-GARCH-MIDAS模型的样本外预测效果,这里取δ1=0.1,δ2=0.9。3个模型的MCS检验结果如表6所示,可以看出使用GARCH-MIDAS模型优于GARCH模型的样本外预测精度,说明高频数据中包含股市波动率预测的信息,并且引入极端冲击和非对称效应提高模型预测精度的结果依旧稳健。 表6 AS-EX-GARCH-MIDAS模型和GARCH模型的MCS检验结果 笔者对GARCH-MIDAS模型进行改进,使其能够捕捉到股市中的极端冲击和非对称效应,通过分析得出如下结论:①从样本内参数估计结果来看,GARCH-MIDAS模型及其拓展模型参数在统计意义上几乎都显著,说明这4类模型适用于上证综指股票市场的研究。在这4类模型中,非对称系数全部显著说明“利空消息”对股市波动率的影响大于“利好消息”。在包含极端冲击的模型中,参数估计结果显示负极端冲击会给股市带来更大的波动,而正极端冲击给股市带来较小的波动且负极端冲击的影响大于正极端冲击,因此股票投资者需要更加关注极端事件以减少损失、合理投资。②从样本外的MCS检验结果来看,在长期项和短期项中均考虑极端冲击和非对称效应的模型的预测性能表现最好,且该结论在稳健性分析中保持稳定。这一结果可为金融政策制定者提供参考意见,为金融市场投资者规避风险。通过对GARCH-MIDAS模型进行改进,丰富了其理论和实际意义,帮助金融市场管理者、政策制定者以及投资者加深对股票市场的认识,为股市波动率的预测提供新的见解,具有一定的理论和现实意义。 从实证结果可以看出探究极端冲击和非对称效应对中国金融市场的影响具有实际意义,可以提高模型的预测精度。未来可以考虑使用笔者提出的基于极端冲击和非对称效应的GARCH-MIDAS模型来研究宏观变量对中国股市波动率的影响。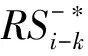
2 实证研究和结果分析
2.1 数据选择及其描述性统计

2.2 样本内估计

2.3 样本外预测
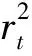

2.4 稳健性分析



3 结论

