数学形态学区域分割的快速相位解包裹算法

李梦霞，曹 博，卢佳玮，崔凯华，刘 乾*

（1. 中国工程物理研究院机械制造工艺研究所，四川绵阳621000；2. 清华大学 精密仪器系，北京 100084）

1 引 言

光学干涉以无损、高精度、高分辨率等优势而广泛应用于高精密表面测量。从干涉条纹中计算的相位被包裹在(-π，π]区间，需要对包裹相位进行解包裹运算，以获得连续的表面高度分布。因此，解包裹是干涉测量中必不可少的关键环节，直接决定了干涉测量的精度与效率。

解包裹算法分为时域和空域两种方式。时域方法获得不同波长对应的相位，根据相位与波长成反比的特点在时域上对相位进行解包裹运算；空域方法根据相邻像素之间的相位差对相位的级次进行判断，进而完成解包裹运算。时域解包裹仅与当前点相位随波长的变化有关［1-2］，可以避免误差沿空间传递，但至少需要两种条纹频率的光源或投影设备［3-4］，而空域解包裹只需要一幅相位图即可求解。一维情况的空域解包裹相对简单和成熟，比较有代表性的是Itoh 方法［5］。Itoh 方法逐个计算相邻像素的相位差，对超出 (-π，π]的相位差加减2π，累加相位差后获得连续相位。依次在行与列方向上应用Itoh 方法，可以简单地实现二维相位的解包裹。但此方式极易受到噪声干扰，误差会随着展开的路径而累积，导致拉丝等错误的结果［6］。

为了解决拉丝的问题，研究人员发展出了多种改进的解包裹算法。这些算法可以分为路径相关和路径无关两大类。路径相关解包裹算法的基本思想是沿着一条选定的连续路径展开相位，其关键在于选择合适的路径。如果路径选择错误，测量噪声会随着路径累加造成较大的误差。路径相关算法主要有枝切法［6-8］、质量图导向法［9］等。枝切法利用连接距离最近的正负残点的枝使解包裹路径避开残点区域，计算速度快，但容易在残点密集区域出现区域性展开误差。质量图导向法按照各点相位质量高低指导解包裹路径，可以避免残点的影响，但是耗时较长。路径无关算法以最小二乘法及其衍生算法为主［10-11］。最小二乘法的基本思想是通过最小化的误差度量滤除局部噪声，能够在一定程度上平滑噪声，但无法限制不可靠数据点引起的相位误差在空间中传播，而且处理时间较长。2018 年Zhang Xiaolei 等人［12］提出了一种基于非二次采样轮廓变换（NSCT）的路径无关相位解包裹算法。NSCT 算法［12-14］以非下采样金字塔滤波器和非下采样方向滤波器对相位图进行滤波和分解，计算不同区域的相位差异后抬升相位，获得连续的相位。NSCT 算法使局部误差无法影响整体的解包裹效果，有效降低噪声的影响，但由于边界提取涉及构造滤波器、多次滤波和分解等复杂运算，耗时过长。

针对干涉测量面临的噪声干扰、相位分布复杂、数据点缺失等实际问题，以及工程实际中对运算效率的要求，本文提出了一种路径无关的快速相位解包裹算法。本方法运用数学形态学工具对包裹相位进行区域分割继而整体展开，具有一定的鲁棒性。本文首先介绍该算法的原理，然后通过仿真和实验验证了该方法的精度、适用性、计算效率等。

2 原理与步骤

二维包裹相位图的特点是：不同级次的相位之间有明显的包裹分界线，在不同级次（区域）内相位是连续变化的。基于此特点，只需确定相邻区域之间相位的相对抬升值，在各区域相位的基础上加上对应的抬升值就能实现整张相位图的解包裹。这是本文相位解包裹算法的基本思想。

数学形态学区域分割（RSMM）解包裹方法的核心在于包裹相位的边界识别和区域分割。数学形态学是建立在格论和拓扑学基础上的图像分析方法，在结构光投影的三维深度分割［15］中有所应用。数学形态学方法的相关算法已经比较成熟，将之与相位解包裹算法结合起来，可以节省运算时间。RSMM 算法的流程如图1 所示（其中加粗的节点为相位数据，未加粗部分为实际操作步骤），各步骤详细描述如下：

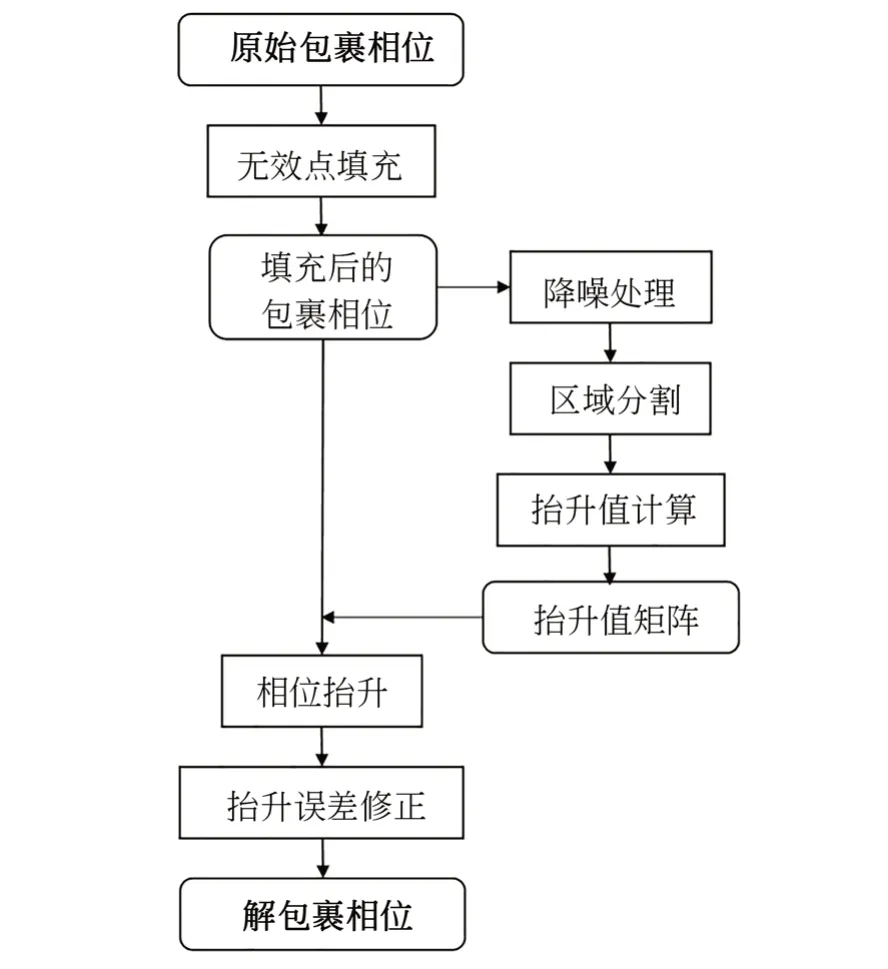
图1 RSMM 解包裹算法原理流程图Fig.1 Flowchart of the RSMM unwrapping algorithm

2.1 无效点填充

在解包裹之前，需要对相位数据缺失的无效点进行填充处理。填充值不能偏离区域极值（±π），且填充值的选择应与其附近的数据有一定的关联，毫无关联的数据会导致错误的结果。另外，填充值用于辅助解包裹，并非完美还原实际数据，因此不用过分追求准确性。根据上述原则，本文采用较为简单、计算量小的移动中位数法［16］进行线性填充，直至所有的无效点都被赋予有效数值，得到填充后的包裹相位。

2.2 降噪处理

包裹相位会存在一些因系统、算法等因素导致的噪声，可能会引起边界的误提取。为了减小噪声导致的边界提取误差，本文采用自适应中值滤波［17］对包裹相位进行去噪处理。

2.3 区域分割

包裹相位在截断处的相邻像素会出现大于π的跳变，表现为梯度的陡变。因此，可以利用包裹相位的梯度识别跳变点以确定相位截断的边界。首先，用Prewitt 梯度算子［18］计算包裹相位的梯度，同时设置合理的阈值（梯度最大值的一半）得到邻位相位差大于π 的点，这些点的集合构成包裹相位的边界。其次，为避免边界断裂，使用膨胀函数将同一条边界上的断裂点连接起来形成完整的边界，进而生成全局的二值图（边界点为逻辑1，区域点为逻辑0）。然后，将二值图中的不同边界分别标记为不同的灰度值。比如，将检测到的第一个边界上所有的点都赋值1，第二个边界上所有的点都赋值2，以此类推，直到所有的边界点都被赋值。此时灰度图像中最大值的大小即代表边界的个数，不同灰度大小的点集即为不同的边界（记为B）。区域的分割与边界分割类似。首先，将全局二值图取反，边界点变为逻辑0，区域点变为逻辑1。其次，将区域二值图中的不同区域分别标记为不同的灰度值，不同灰度大小的点集分别代表不同的区域（记为R）。相位图的边界类似于等高线，本质上是相同高度点的集合。因此，边界线不会出现交叉，区域数量最多比边界数量多1 个。实际操作中可根据这一特点将误提取的区域删去，融入邻近的边界或区域。然后，对边界进行小系数膨胀，膨胀后的边界（记为DB）作为后续操作的判别工具。

图2 为peaks 函数生成包裹相位图中划分的边界和区域示意图，图中B表示边界，R表示区域。

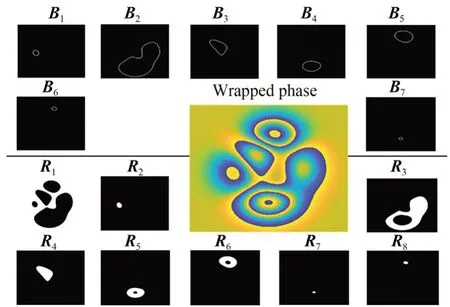
图2 相位图分割示意图（白色表示选中的区域）Fig.2 Diagram of phase segmentation（white represents the selected area）

2.4 抬升值计算

2.4.1 区域抬升值

为了计算不同区域的相对抬升值，需要明确区域之间的位置关系，因为只有相邻区域间才有明确的相对相位抬升值。借助膨胀的边界与原始的区域来判断不同区域是否相邻，然后计算相邻区域的相对相位抬升值。

结合图3 描述的具体做法为：以图2 中的边界B1为例，首先，将其膨胀后的边界DB1分别和所有区域（Rj，j=1、2……）取交集，若DB1只有和R1、R2的 交 集 不 为 空 集 ，则R1和R2是 被B1分 割开的相邻区域。以图3 为例，R1和DB1的交集表示在R1内部且靠近B1的点的集合，R2和DB1的交集表示在R2内部且靠近B1的点的集合。将边界和区域的交界点的集合记为上标i表示区域标号，下标j表示边界标号。在包裹相位中计算点集的相位中值，以表示。与同一边界Bj相邻的两个区域Rm和Rn，其各自交界点集的相位中值为区域Rm相对Rn的抬升值可以计算为：

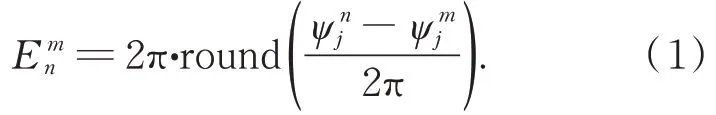
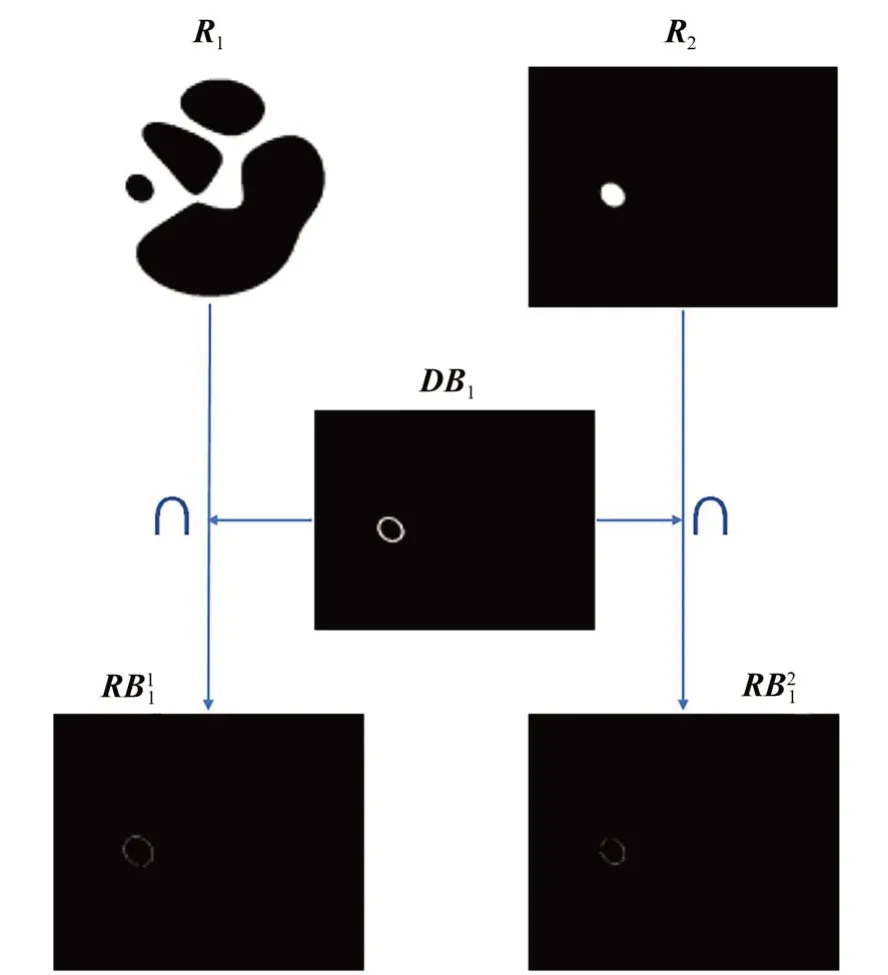
图3 区域相邻关系判断示意图Fig.3 Diagram of determining the relation between adja⁃cent areas

通过上述方法可以确定所有相邻区域的相对抬升值，最后以某个区域为标准（例如设R1的绝对抬升值Er1为0），根据各区域的位置关系和相对抬升关系可确定所有区域的绝对抬升值Erj。

2.4.2 边界点抬升值

在上一步中只计算了各区域的抬升值，而边界点比较复杂，需要逐点判断。边界Bj上的点bj(x，y)的包裹相位值为φ(x，y)，利用它与相邻边界相位中值之间的相对大小判断其归属，进而确定其抬升值，计算如下：

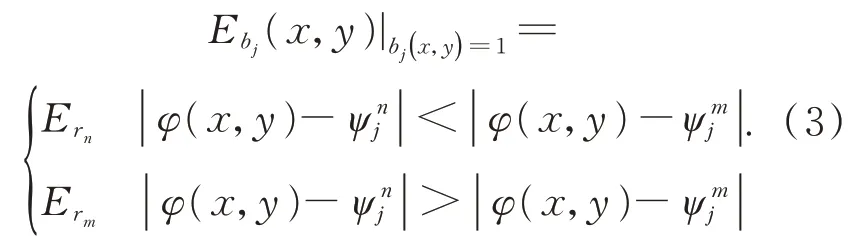
通过上述步骤，可以确定不同区域和边界上的点的绝对抬升值，记录这些抬升值并建立全局抬升值矩阵。

2.5 相位抬升

为避免降噪处理等步骤改变原始包裹相位的值，对解包裹结果产生干扰，因此在无效点填充后的原始包裹相位的基础上进行相位抬升。填充后的包裹相位经（2）（3）（4）步骤获得抬升值矩阵，与其本身相减即可得到抬升后的相位。

2.6 抬升误差修正

由于依据式（3）计算的相位抬升值在少量边界点处存在偏差，进而引起边界抬升误差。抬升误差点与周围正确点的抬升值相差2π 的整数倍，导致抬升后误差点与周围点相位差绝对值大于π。理论上抬升后相位的相邻像素不应有超过π的跃变。根据这一原则，确定误差点的位置，做局部中值滤波以修正抬升误差。如果包裹相位存在无效点，则在解包裹后的相位中将填充的数据还原成无效值，得到最终的解包裹相位。

RSMM 算法优势在于：（1）使用成熟的数学形态学算子对包裹相位进行边界分割和抬升值判断，计算量小，准确度高；（2）包裹相位的无效点不影响区域的判断，能够实现含缺失数据的相位解包裹；（3）抬升值在区域上整体计算，而只在边界逐点计算，省去了大量的相位比对时间，且局部区域噪声不会影响全局的解包裹效果。

3 计算机仿真

通过计算机仿真对RSMM 算法的计算精度、耗时、适用性进行了验证。仿真所用计算机CPU 主频为 3.00 GHz，内存频率为 2 667 MHz。

3.1 计算精度

以peaks 函数作为基础相位，生成含有密度为0.1、幅值为π/5 rad 的椒盐噪声的真实相位，并将其压缩在 (-π，π]，得到 500×500 pixels 的包裹相位，如图4 所示。可以看出，包裹相位中存在明显的噪声分布。先对包裹相位图进行自适应中值滤波，然后利用数学形态学算子提取边界（如图5 所示），计算解包裹相位与真实相位的点对点残差，如图6 所示。残差的RMS 值为4.4×10-16rad，表明RSMM 方法具有足够高的精度，能够获得精确的解包裹相位。又经过仿真验证了不同幅度噪声对结果的影响，所加相位噪声幅度在0~π/2 范围内，解包裹残差RMS 值均在10-16rad 量级。这是因为区域分割过程中采用了降噪处理，噪声基本不影响边界处理结果。为比较解包裹的效果，同时采用了NSCT 算法和最小二乘算法对相位进行解包裹。三种算法的残差RMS 都在10-16rad 量级，表明三种方法均能正确解包裹，且精度相当。然而，本文方法所需要的计算时间仅为 0.3 s，远小于 NSCT 算法（13.3 s）和最小二乘算法（2.9 s）。

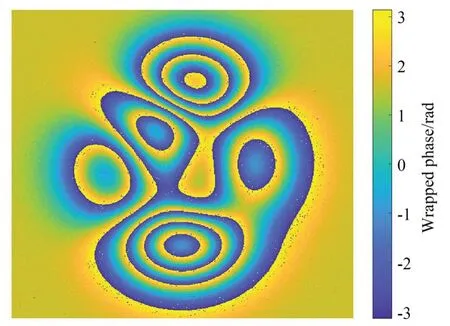
图4 含噪声的peaks 包裹相位Fig.4 Noised wrapped phase of peaks

图5 提取的边界Fig.5 Extracted boundaries

图6 RSMM 算法解包裹相位的残差Fig.6 Residual error map of unwrapped phase with RSMM algorithm

3.2 计算时间

由于RSMM 算法需要对包裹相位进行分区域计算，因此计算时间会受条纹数量的影响，条纹越多、区域越多，则耗时越长。保持数据图大小为 500×500 pixels 不变，调整 peaks 函数的整体高度，从而改变包裹相位图的条纹数。记录不同包裹条纹数相位解包裹所用时间，并对三种算法进行比较，如图7 所示。图中可以看出，RSMM 算法用时最短，仅为最小二乘法的10%、NSCT 法的1.7%。由于NSCT 算法将不同频率子代下不同方向的边界融合，又采用区域生长法进行边界膨胀。提取的边界比实际大，在条纹密集区域出现相位抬升错误。当条纹超过一定密度（6 根/100 像素）以后，NSCT 解包裹算法不能准确地求解，因此未记录N>12 以后的计算时间。

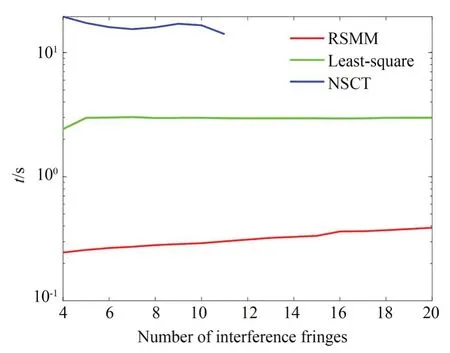
图7 三种算法耗时随条纹数量的变化Fig.7 Calculation times of three algorithms with respect to the fringe number

除条纹数量外，图像大小也会影响解包裹算法的效率。固定条纹数量为8，对包裹相位的像素数量进行调整，测试从200×200 pixels到 2 000×2 000 pixels 不同像素数量的解包裹运算时间。如图8 所示，三种算法的计算时间均随像素数增加而增加，其中RSMM 算法计算时间最短，且随像素数量增加最慢。这是因为RSMM算法只计算边界处像素的相位，计算量随整体像素数量增长较缓慢。

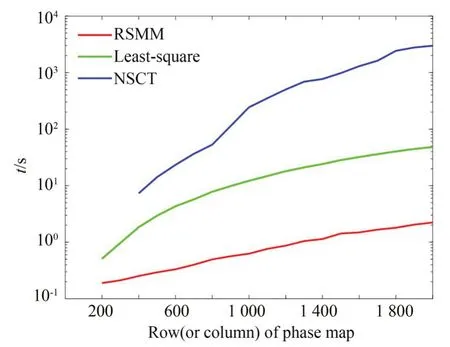
图8 三种算法耗时随相位图大小的变化Fig.8 Calculation times of three algorithms with respect to the phase map size

3.3 复杂相位的适用性

在实际测量时得到的相位可能会因为表面区域分布、污染等情况导致相位数据缺失，存在较复杂的无效点分布。为测试算法的适用性，在生成peaks 相位时加入了复杂分布的无效区域（如图9）。当包裹相位图中存在无效点时，RSMM 算法能够准确解包裹，如图10（a）所示。而NSCT 解包裹算法出现边界识别错误且后续无法计算，最小二乘算法也出现解包裹错误，如图10（b）所示。

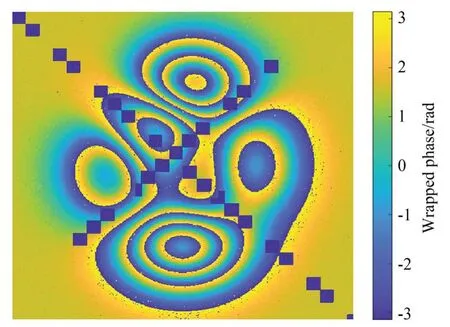
图9 含无效点的包裹相位Fig.9 The wrapping phase with data dropout

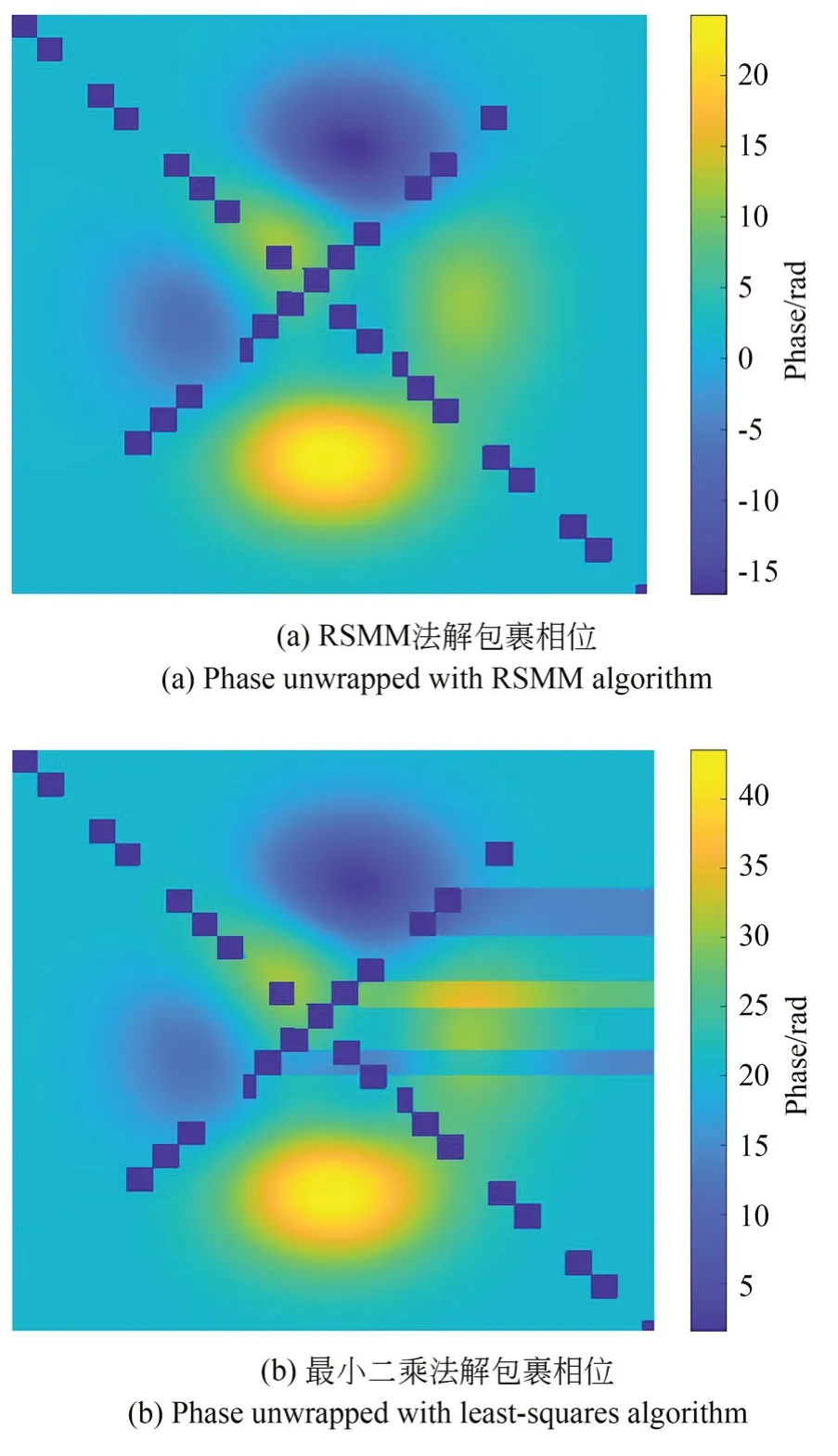
图10 含无效点的包裹相位解包裹效果Fig.10 Unwrapped phase with data dropout

计算机仿真表明，RSMM 算法具有计算精度高、抗噪能力强、运算耗时短、适应性强等优点。这些优点源于：区域分割等数学形态学工具的应用提升了边界提取的准确性和效率；相位图进行分区域整体抬升提高了解包裹精度和效率；解包裹前使用移动中位数法线性填充无效点和自适应中值滤波处理噪声，增强了算法的鲁棒性和适应性。

4 实验验证

为测试RSMM 算法解包裹的实际效果，采用干涉显微镜分别测量超精密车削工件、标准台阶和表面有瑕疵的平面反射镜。

车削表面的包裹相位如图11 所示。采用三种方法对车削表面相位解包裹，结果如图12 所示。RSMM 法和最小二乘法解包裹得到了比较一致的准确结果，而NSCT 解包裹结果中部分区域出现抬升错误。标准台阶标称高度为80 nm，其包裹相位如图13 所示。虽然台阶表面自身存在梯度剧变，但在边界提取时设置了阈值，台阶边缘并未影响到解包裹效果。RSMM 算法对标准台阶相位解包裹并校平后的结果如图14所示。在商业设备中计算得到台阶高度为85.639 nm，RSMM 算法解得高度为85.686 nm，最小二乘法解得高度为85.698 nm，NSCT 算法解得高度为85.769 nm，三种算法精度相当。对于这两种测量对象的包裹相位，三种算法解包裹的运算时间如表1。可以看出，RSMM 算法的计算时间仅为最小二乘方法的1/4、NSCT 算法的1/5。

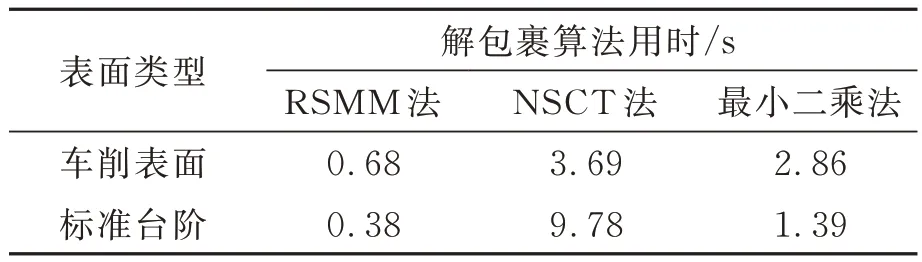
表1 三种解包裹算法用时Tab.1 Calculation times of three unwrapping algorithms

图11 车削表面包裹相位Fig.11 Wrapped phase of the turned surface

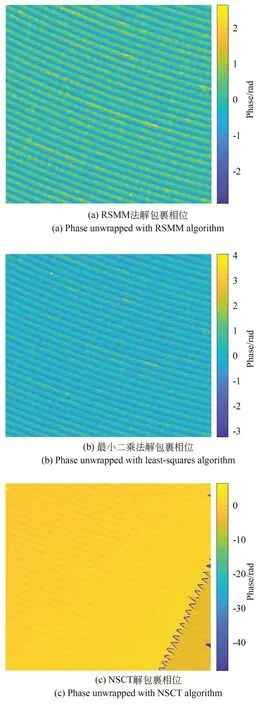
图12 车削表面解包裹相位Fig.12 Phase unwrapped of the turned surface

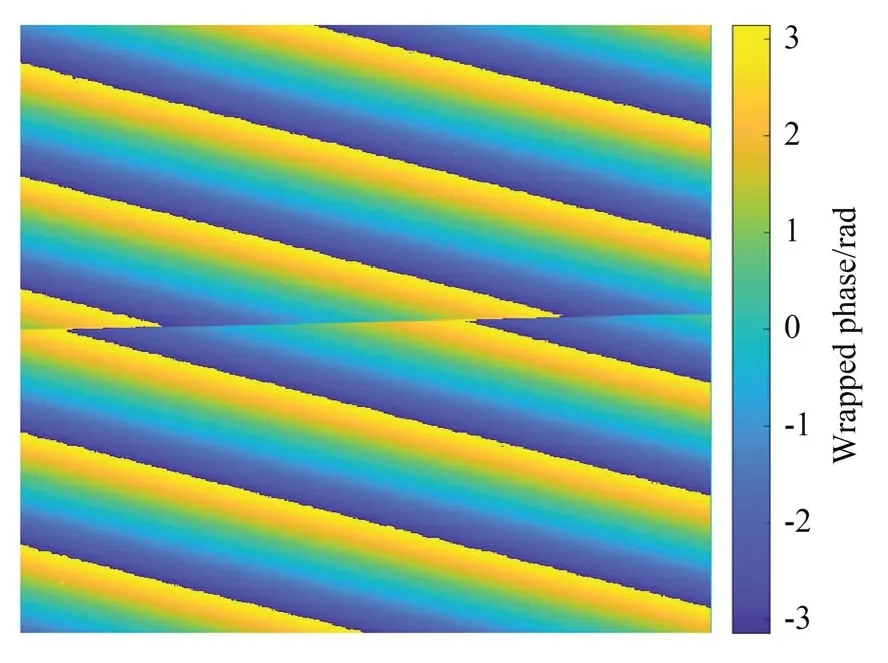
图13 标准台阶包裹相位Fig.13 Wrapped phase of the standard step

图14 RSMM 解包裹标准台阶相位Fig.14 Phase unwrapped of the standard step with RSMM algorithm

图15 为表面有瑕疵的平面反射镜的包裹相位，其边界和区域内部均有不规则的数据缺失，边缘毛糙，噪声较大。RSMM 法和最小二乘法解包裹的相位如图16 所示，而NSCT 解包裹算法无法处理含无效点的数据故未给出结果。从图中可以看出，虽然包裹相位含有较多不规则分布的无效数据，但RSMM 算法仍然能够正确解包裹且达到较好的效果，而最小二乘法则出现了错误结果。镜面的表面粗糙度经商业仪器测得为9.4 nm，RSMM 算法求得的粗糙度为10.1 nm ，误差可能源于数据处理过程中的滤波、阈值等处理环节的差异。

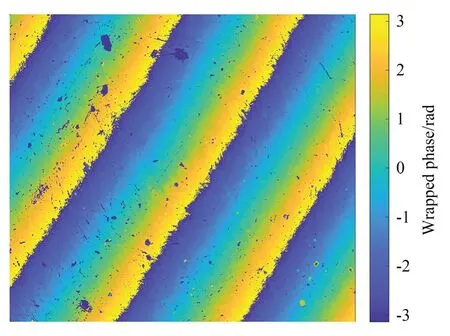
图15 平面反射镜的包裹相位Fig.15 Wrapped phase of the mirror

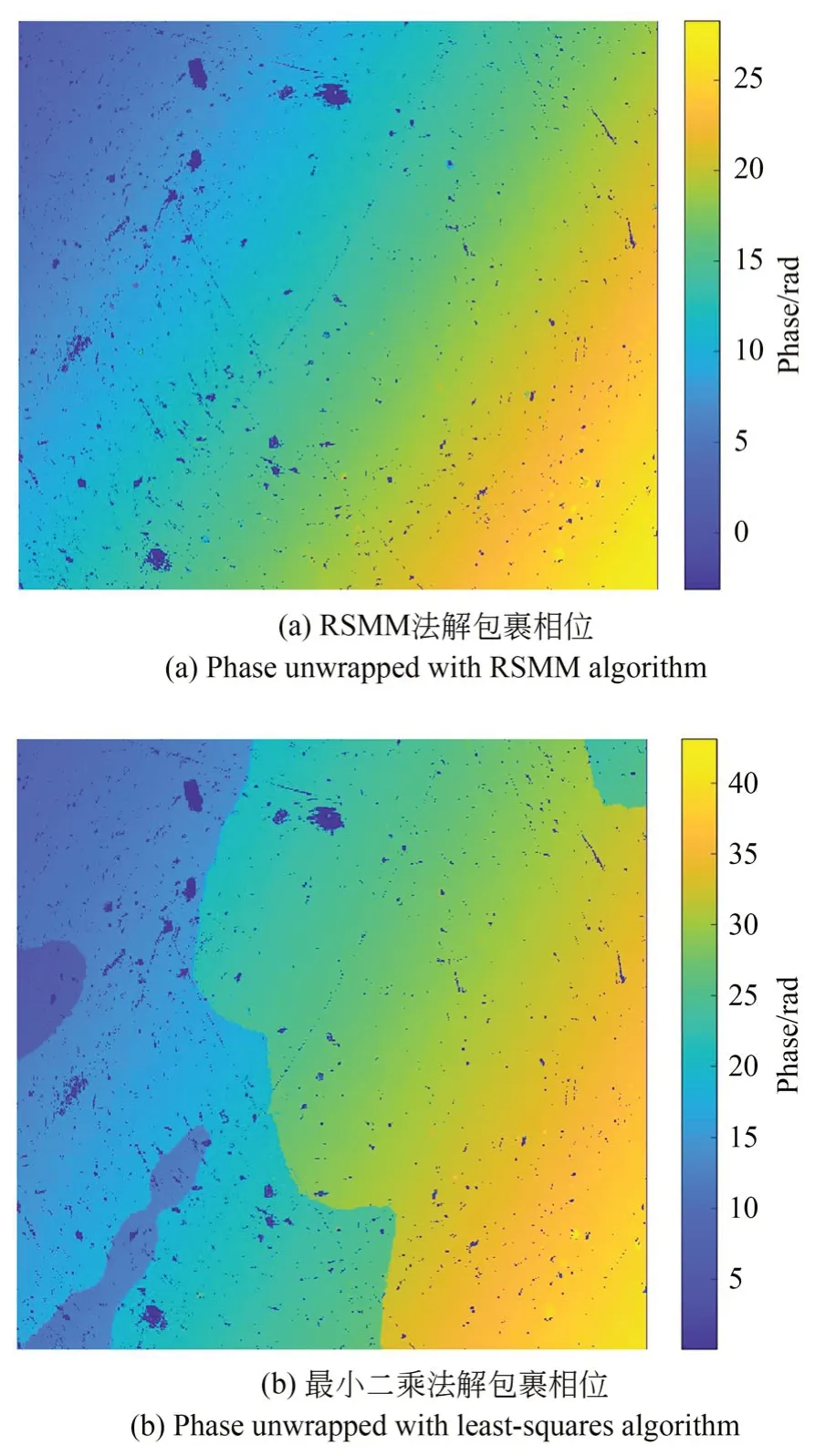
图16 平面反射镜的解包裹相位Fig.16 Phase unwrapped of the mirror

5 结 论

本文提出的RSMM 算法能够快速解算包裹相位，精度与传统算法相当，并且能够有效处理随机噪声干扰等实际问题。该算法适应性强，对于条纹密度高的包裹相位、部分区域数据缺失的复杂包裹相位，都能实现准确的全局解包裹。仿真和实验结果证明：RSMM 算法残差RMS 值可以达到 10-16rad 量级，对 1 000×1 000 pixels 的包裹相位解算时间在1 s 以内，仅为经典的最小二乘算法用时的1/4。本文只展示了RSMM 算法应用于干涉测量的效果，这种算法也可以扩展到其他需要相位解包裹的领域，如数字全息、光栅条纹投影轮廓测量等。