基于灰狼算法的模块化关节摩擦辨识和补偿

崔靖凯，赛华阳，张恩阳，朱明超 ，徐振邦，3*

（1. 中国科学院长春光学精密机械与物理研究所，吉林长春130033；2. 中国科学院大学，北京 100049；3. 中国科学院大学材料与光电研究中心，北京100049）

1 引 言

模块化关节能通过重构组合，使机械臂形成不同功能的构型，满足不同环境和任务的需求。具有模块化关节的机械臂制造成本低、设计周期短、互换性强并易于改进，被广泛应用于各个领域［1］。为了获得高负载自重比，模块化关节常具有谐波减速器等非线性环节，这增大了摩擦干扰，影响机械臂的定位和跟踪精度。

摩擦补偿是减少或消除关节非线性环节的不利影响、提高系统动态性能的重要途经。摩擦补偿包括基于摩擦模型的补偿和不基于摩擦模型的补偿。其中，基于摩擦模型的补偿由于具有可预见、响应速度快等特点［2］，获得了广泛应用。模块化关节的摩擦模型包括库伦-黏性摩擦模型［3］、Stribeck 摩擦模型［4］、LuGre 摩擦模型［5］等。库仑-黏性摩擦模型和Stribeck 摩擦模型无法描绘电机速度接近于零时的预滑动区域的摩擦特性，导致电机速度换向时补偿的摩擦力不连续，引起力矩的跳变。为了充分考虑摩擦的非线性特性，保证补偿力矩的连续性，本文基于LuGre摩擦模型进行摩擦补偿。

摩擦模型参数的准确度直接影响了摩擦模型的精度，进而影响摩擦补偿的效果［6］，因此需要对模型参数进行辨识。参数辨识是指在满足激励的条件下，采集系统的状态信息对物理参数进行估计的过程［7］。参数辨识可以分为在线辨识和离线辨识。在线辨识适用于对环境变化敏感的参数，如温度的变化、材料的磨损等，虽然具有高精度和实时响应的优点，但可能存在参数收敛不完全的问题，且受到实验对象能否实时执行的限制。离线辨识相对简单易行，在对环境变化不敏感的参数如力矩系数、摩擦系数等上更具优势，因此，本文采用离线辨识的方法。

针对LuGre 模型，学者们提出了多种辨识方法。肖前进［8］等用分段最小二乘法辨识了LuGre模型的静态参数，将电机预滑动区域的特征作线性化处理，等价为一个二阶系统，计算得到动态参数。该方法需要对实验数据分段辨识，预滑动区域的线性化处理会引入建模误差、计算误差等，影响辨识精度。为了提高辨识精度，元启发式算法成为研究热点。于伟［9］等用一般辨识方法辨识了静态参数，并以转速变化为目标函数，用遗传算法拟合出动态参数；曾德林［10］等用分步夹逼和分步搜索法初步辨识了摩擦参数，然后用遗传算法提高辨识精度。

灰狼算法是由SEYEDALI M［11］提出的元启发式优化算法，模仿自然界中灰狼的领导阶层和捕猎机制。灰狼算法具有简单易用、灵活性强和避免局部最优等优点，适用于多参数辨识的情况。相较于工程常用的最小二乘法，无需对数据分段处理，在辨识非线性模型方面具有优势。

本文针对自主研发的模块化关节，选用能较为全面地描述摩擦特性的LuGre 模型，分别用基于分段最小二乘法的一般辨识方法和基于灰狼算法的元启发式辨识方法对摩擦参数进行辨识，并将辨识结果对比分析，最后通过前馈补偿算法对摩擦力进行补偿。实验结果表明，相比于一般辨识方法，灰狼算法在摩擦辨识领域精度更高、适用性更强；本文提出的摩擦补偿方法能显著减小关节速度跟踪误差，提高控制品质。

2 模块化关节系统及建模

2.1 关节结构

图1 为模块化关节的内部构造示意图。关节主要由外壳、无框力矩电机、谐波减速器、电磁制动器、增量式编码器、绝对式编码器和驱动电路板构成。左侧和下侧的电连接板用于给相邻关节供电通讯，方便关节的装卸和组合，体现模块化的特点。关节采用双编码器设计，增量式编码器获取的相对位置信息通过差分运算得到速度信息，绝对式编码器用于获取关节负载端的绝对位置信息。

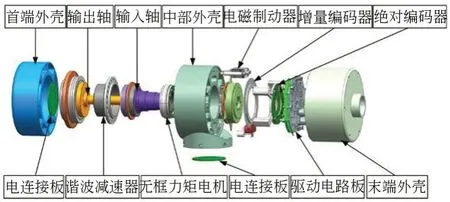
图1 模块化关节结构图Fig.1 Structure of modular joint

2.2 控制系统

关节采用位置-速度-电流三闭环控制，控制框图如图2 所示。计算机使用倍福公司的Twin⁃CAT 软件对关节发送指令，关节的驱动电路板接收到位置或速度指令，通过控制q轴电流驱动电机转子和输入轴转动，谐波减速器的波发生器与输入轴固连，经减速后的输出轴与负载连接，实现力矩的输出。

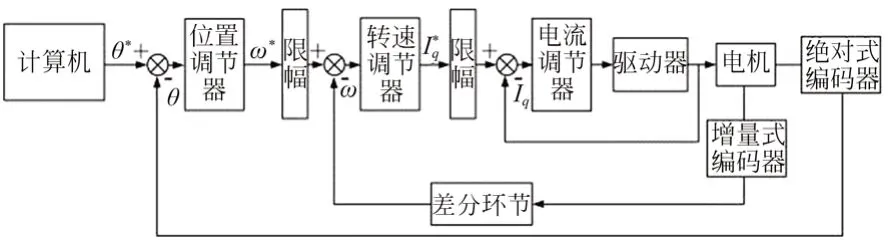
图2 模块化关节控制框图Fig.2 Block diagram of modular joint control system

2.3 动力学模型

建立模块化关节的简化动力学模型如图3 所示，其动力学方程为：

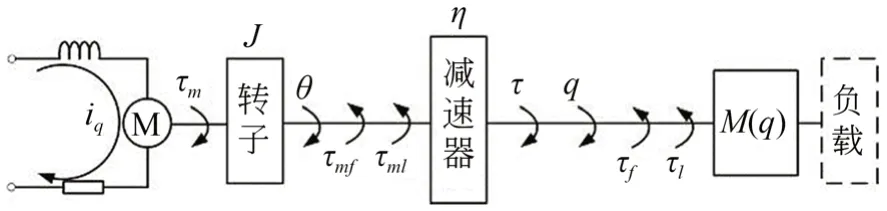
图3 模块化关节动力学模型Fig.3 Dynamic model of modular joint

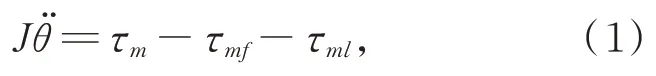
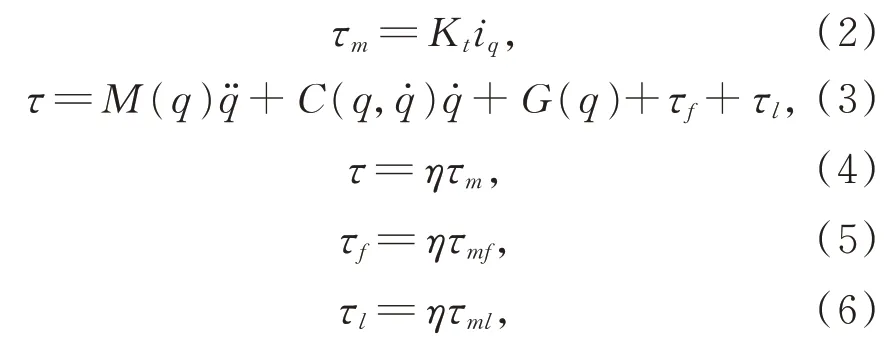
其中：J为电机转子及波发生器折算到电机端的转动惯量；θ为电机转角；τm为电机端输出力矩，τmf和τml分别为折算到电机端的摩擦力矩和负载力矩；Kt为力矩系数；iq为q轴电流；τ为关节端输出力矩分别为关节端角度、角速度、角加速度；M(q)q̈为连杆惯性项为离心力和科氏力项；G(q)为重力项；τf和τl分别为关节端摩擦力矩和负载力矩；η为谐波减速器的减速比。为了统一度量，本文均采用关节端的物理量作为实验和计算数据。

3 摩擦参数辨识

3.1 LuGre 摩擦模型

摩擦来源于接触器件的相对运动。对于模块化关节，谐波减速器的波发生器和柔轮的相对运动、柔轮和钢轮的相对运动都会产生摩擦。此外，电机输入轴、输出轴的支撑轴承也存在摩擦。

LuGre 摩擦模型为：

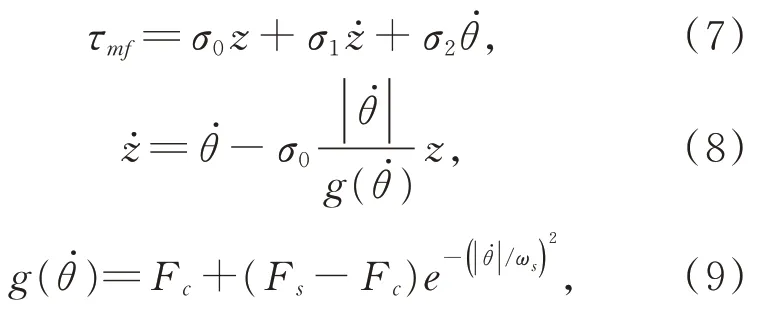
其中：z为鬃毛平均形变量，σ0为鬃毛刚度，σ1为鬃 毛 阻 尼 系 数 ，σ2为 黏 滞 摩 擦 系 数为Stribeck 效应，Fc为库仑摩擦力，Fs为最大静摩擦力，ωs为Stribeck 速度。模型包括四个静态参数Fc、Fs、ωs和σ2，以及两个动态参数σ0和σ1。

3.2 基于分段最小二乘法的一般辨识方法

一般辨识方法分为两步，第一步将实验数据分段，用最小二乘法分别辨识电机转速为正和转速为负时的摩擦静态参数；第二步将转速为零附近的预滑动区域作线性化处理，使其近似为二阶系统，然后辨识该系统的幅频特性，计算得到动态参数。

3.2.1 静态参数的辨识

此时关节的输出力矩主要克服摩擦力矩。

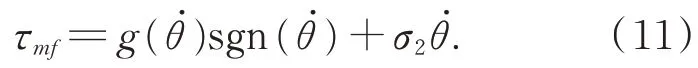
结合式（1）和（2），在电机空载匀速转动的条件下，有：

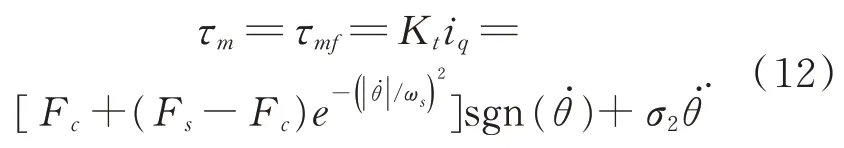
因此，可以测出电机在不同速度下匀速转动时的q轴电流，乘以力矩系数Kt=0.21 N·m/A得到摩擦力矩，绘制摩擦力-速度曲线。

图4 是摩擦参数辨识和补偿平台。关节空载且水平放置，计算机的TwinCAT 软件用于控制电机匀速转动，MATLAB 软件用于数据的处理和分析。计算机和关节驱动板用网线连接，通信协议为倍福公司的EtherCAT。实验时，采样周期设置为5 ms，关节端速度变化范围为-35（°）/s到-0.5（°）/s 和 0.5（°）/s 到 35（°）/s，每次改变0.5（°）/s，每个速度维持 15 s。为了消除电机在启动和停止阶段的电流波动，取中间5 s 的q轴电流值的平均值作为该速度下的电流值。根据式（12）计算出每个速度对应的摩擦力，用分段最小二乘法拟合摩擦力-速度曲线，结果如图5 所示。

图4 摩擦辨识和补偿平台Fig.4 Platform of friction identification and compensation

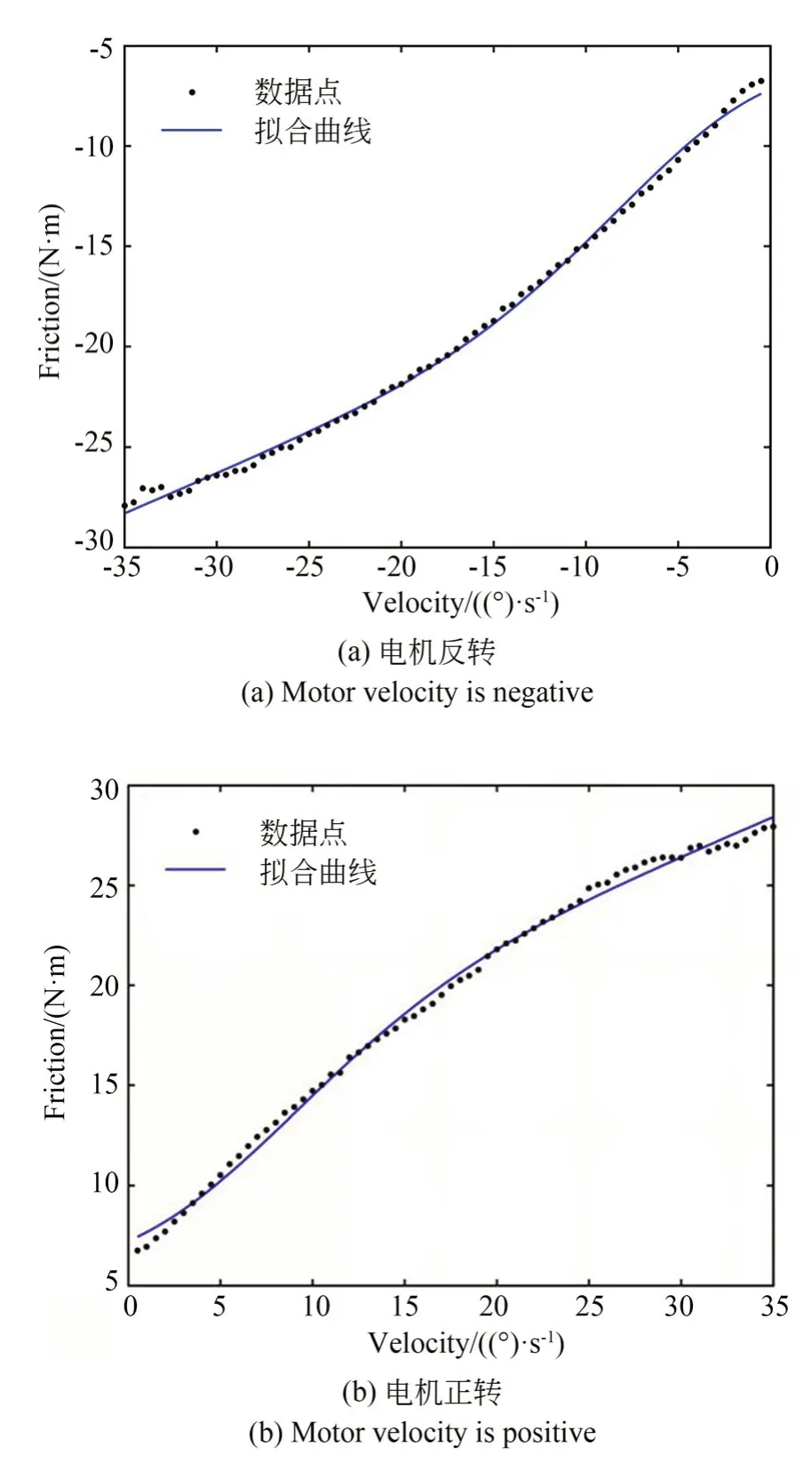
图5 摩擦拟合曲线Fig.5 Fitting curves of friction torque

按照式（12）辨识的静态摩擦参数如表1所示。

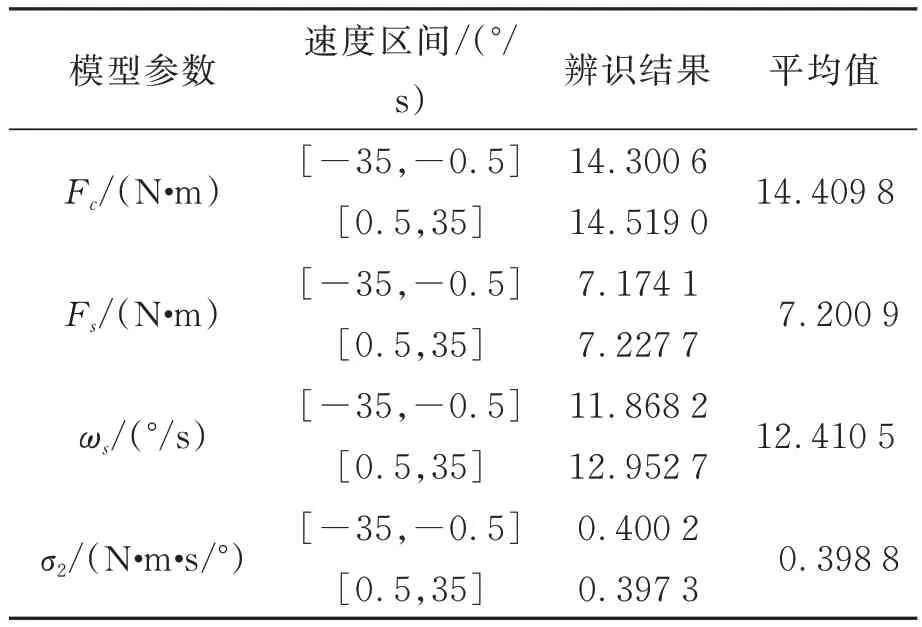
表1 静态参数辨识结果Tab.1 Identification results of static parameters

3.2.2 动态参数的辨识

在电机的预滑动区域，即驱动力矩小于最大静摩擦力矩时，对方程（7）在零状态和零速度附近作线性化处理，即令得到：

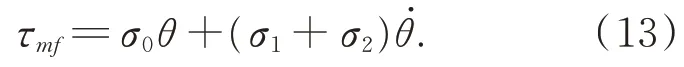
关节空载即τml=0 时，结合式（1）和（2），得到：

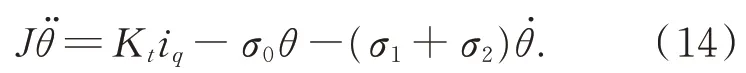
式（14）在频域中的表达可写成：

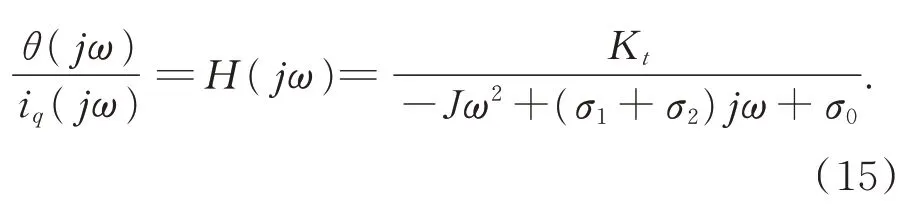
由此可见，在预滑动区域，LuGre 模型表现为带有阻尼的质量-弹簧二阶系统。可以通过伪随机序列测试该二阶系统的幅频特性，分析伯德图和拟合的频响函数获得动态参数σ0和σ1的估计值。

实验时，以幅值为0.19 A，长度为511 位，周期为2 s 的M 序列作为q轴电流值输入关节系统。该序列满足准白噪声要求，其自相关函数可近似为δ函数。序列幅值的均方根值对应的关节驱动力矩为6.65 N·m，小于最大静摩擦力7.200 9 N·m，可防止系统离开预滑动区域。测量的系统响应为电机的转角θ。为了排除非零初始条件的影响，输入4 个周期的M 序列，测出后3个周期的系统响应并做平均处理。图6 展示了其中一个周期的M 序列和系统响应曲线。

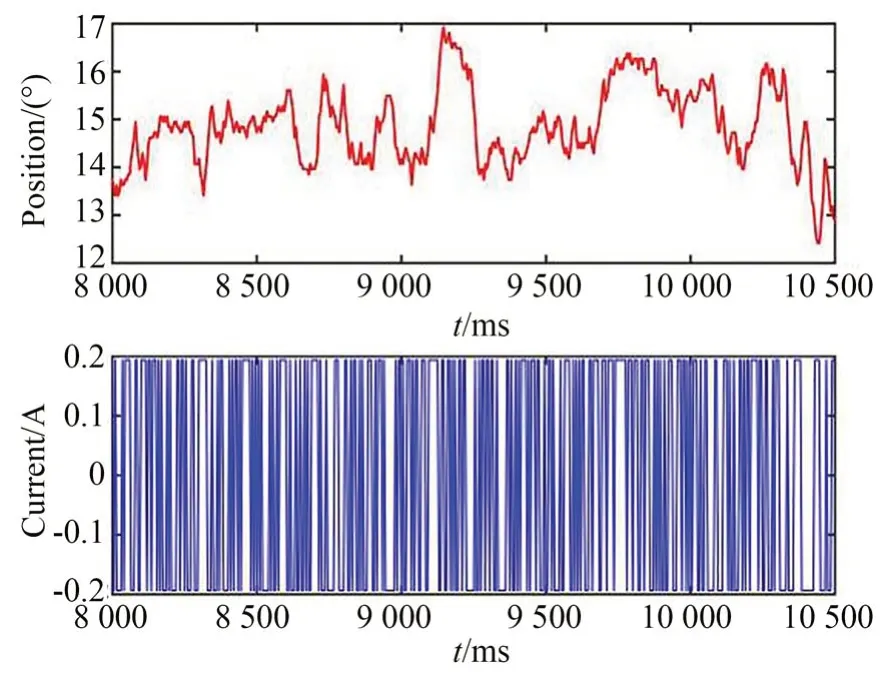
图6 伪随机序列和系统响应Fig.6 Pseudo-random sequences and system responses

用相关分析法将系统辨识为二阶系统，得到频响函数H(jω)。在ω=0 时，由式（15）得到：

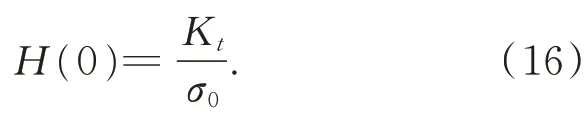
因此可以得到σ0的估计值。再根据式（15）计算σ1的估计值，辨识结果如表2 所示。

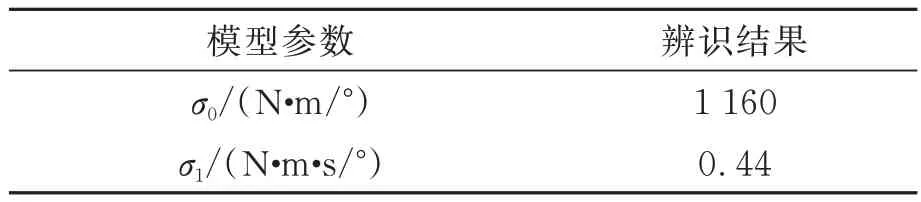
表2 动态参数辨识结果Tab.2 Identification results of dynamic parameters

3.3 基于灰狼算法的元启发式辨识方法

灰狼算法（GWO）是一种新的元启发式算法，灵感来自灰狼社会的狩猎行为。GWO 的种群代表一群狼，根据灰狼的适应度将其分为4 个阶级：最优解称为α 狼，次优解称为β 狼，再次优解称为 γ 狼，其余解称为 ω 狼。

α，β和γ是搜索猎物的领导者，ω狼通过以下算子来更新它们的位置，以跟随三只头狼到达搜索空间的最佳区域：

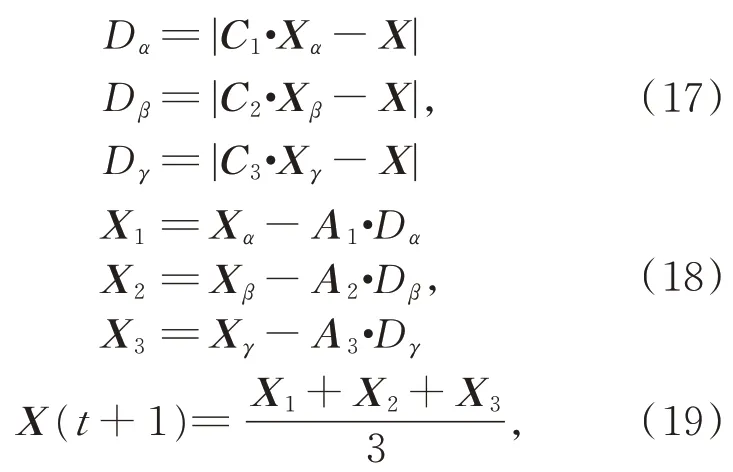
其中：Dα，Dβ和Dγ分别是狼群ω与头狼α，β和γ的距离；X，Xα，Xβ和Xγ分别是狼群ω、头狼α，β和γ当前迭代次数下的位置向量；X（t+1）是狼群ω下一次迭代的位置向量，t是当前迭代次数；Ai和Ci（i=1，2，3）是随机生成的系数向量，如下所示：

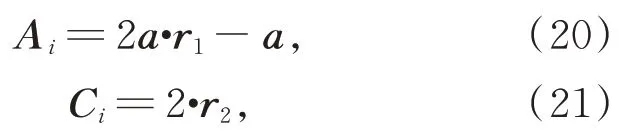
其中：r1和r2是区间［0，1］中的随机向量；a的值在迭代过程中按照下式从2 线性减小到0：

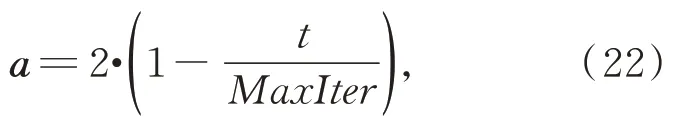
其中MaxIter是最大迭代次数。

图7 展示了狼群如何在二维搜索空间内更新其位置。可以观察到，最终位置将位于由搜索空间中头狼α、β 和γ 所定义的圆内的随机位置。换句话说，α、β 和 γ 估计猎物的位置，其他狼随机更新至猎物周围的位置。随机向量Ai和Ci是该算法需要调节的两个参数。|Ai|<1 时，灰狼会向猎物进攻，而|Ai|>1 时，灰狼会被迫逃离猎物，这允许灰狼进行全局搜索。|Ci|始终是区间［0，2］中的随机值，它将提供随机权重，以强化（|Ci|>1）或弱化（|Ci|<1）猎物在式（17）中定义距离的效果。Ci也可视为自然界中障碍物对灰狼接近猎物的影响，它有助于灰狼突破局部最优停滞。

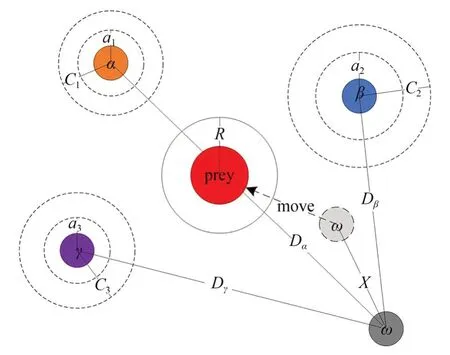
图7 GWO 位置更新示意图Fig.7 Position updating in GWO

在LuGre 摩擦模型的辨识中，该算法所处理的猎物是式（7）到（9）所包含的6 个参数。定义目标函数为：

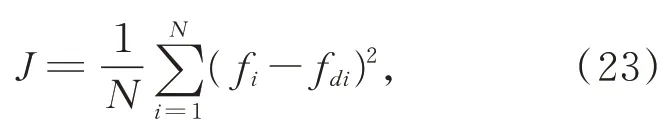
其 中 ：N是 样 本 数 ，fi和fdi分 别 是 第i次 采 样 的模拟摩擦力和实际摩擦力。该问题是最小化寻优问题，即目标函数越小，灰狼的适应度越高。

图8 展示了灰狼算法的操作流程。实验时，参数约束设置为：Fc∈［0，20］，Fs∈［0，10］，ωs∈［0，20］，σ2∈［0，1］，σ0∈［0，30000］，σ1∈［0，1］，狼群规模设置为50。因为算法是随机搜索的，故用不同的初始种群进行了10 次重复运算，并在200 次迭代后停止运行。图9 展示了在不同的初始种群下，α 狼（最优解）的目标函数随迭代次数的演变过程。

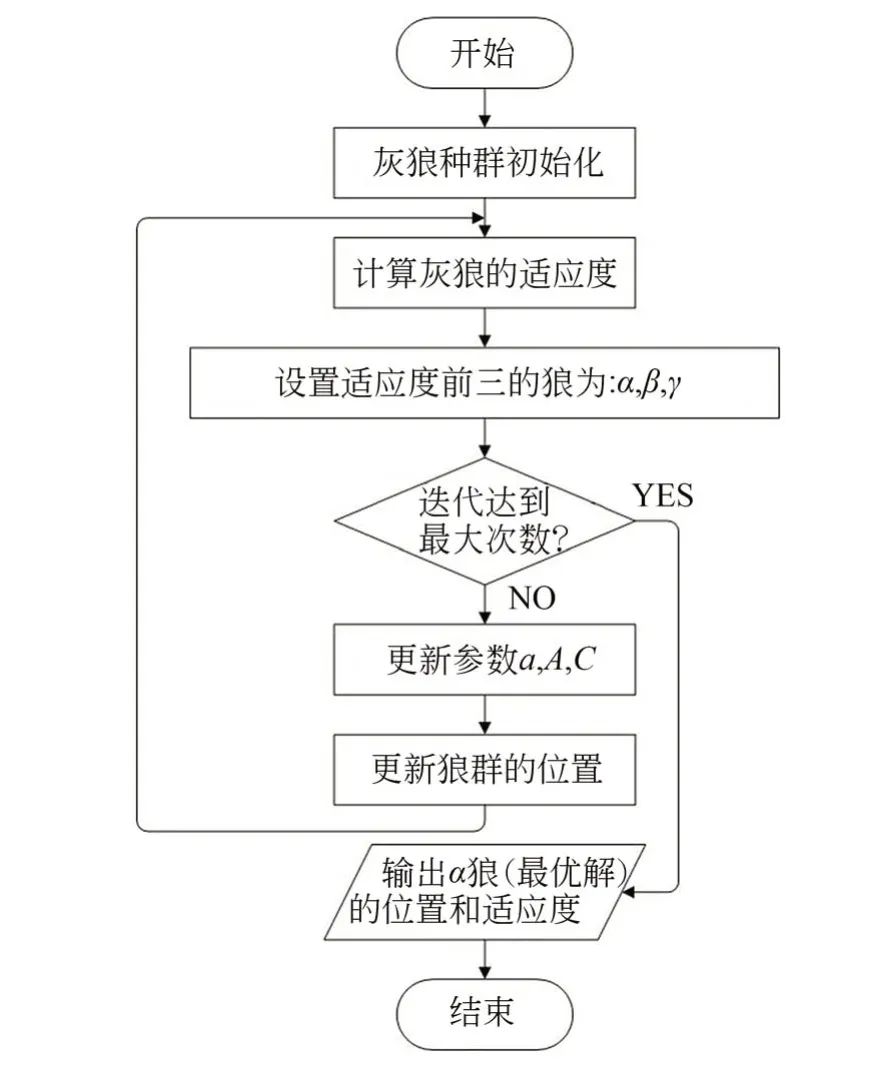
图8 GWO 算法流程Fig.8 Flowchart of the GWO algorithm

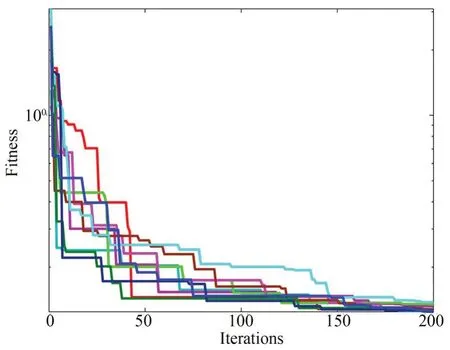
图9 不同初始种群下GWO 的收敛曲线Fig.9 Convergence curves of the GWO algorithm with different initial population

可以看出，十次重复运行的结果都成功地收敛到最优参数附近，最佳运行的第38 次迭代和最差运行的第158 次迭代的目标函数都达到了10-0.84。一些运行在搜索过程中陷入了局部最优，但在最后的几次迭代中都成功地突破停滞，走向全局最优。

基于灰狼算法的辨识结果如表3 所示。

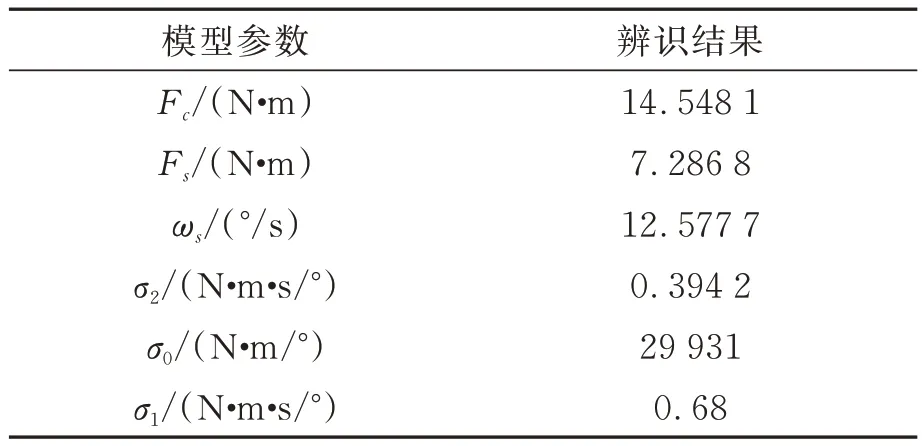
表3 基于灰狼算法的辨识结果Tab.3 Identification results of parameters based on GWO

3.4 两种算法的对比

选择式（23）作为辨识精度的衡量指标。J代表辨识结果和实验数据之间的误差，J越小，辨识精度越高。基于分段最小二乘法的一般辨识方法和基于灰狼算法的元启发式辨识方法的对比如表4 所示。由此可见，灰狼算法的辨识精度高于一般辨识方法，且无需对实验数据分段辨识，无需对预滑动区域作线性化处理，避免了建模误差和计算误差，在摩擦辨识领域具有更强的竞争力。

表4 两种摩擦参数辨识算法对比Tab.4 Comparison of two friction parameter identification algorithms

4 摩擦补偿及实验

为验证摩擦辨识的准确性，改善模块化关节的动态性能，设计了图10 所示的基于摩擦模型的前馈补偿算法。关节仍采用位置-速度-电流三闭环控制，取期望的电机端速度值为摩擦补偿器的输入，按照式（7）到（9）计算相应的摩擦补偿值τc，除以力矩系数得到补偿电流值Iqc，作为前馈量叠加到电流环的输入端，以消除摩擦扰动。

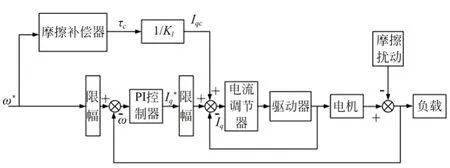
图10 摩擦补偿算法框图Fig.10 Block diagram of friction compensation algorithm

关节输出角度的跟踪精度很大程度上取决于速度的跟踪精度，因此取关节的角速度作为观测量。实验采用图4 所示的设备，摩擦补偿前，测得模块化关节的速度环带宽为12 Hz，实验时，给定幅值为 1（°）/s，频率为 10 Hz 的正弦关节端速度输入信号sin（20πt），加入摩擦补偿前后的关节端速度曲线、摩擦补偿值曲线、速度跟踪误差曲线如图11 所示。

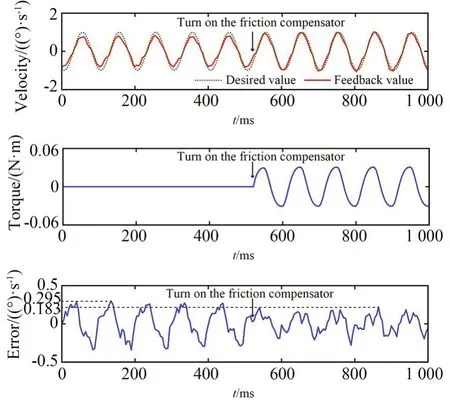
图11 摩擦补偿结果Fig.11 Results of friction compensation

图11 中，在箭头所标注的时刻开启摩擦补偿器，可以看到摩擦补偿后，实线代表的速度反馈值能更好地跟踪虚线代表的速度期望值，跟踪误差显著减小，由补偿前的峰值0.295（°）/s 减小到补偿后的峰值0.183（°）/s，降低了38%。改变输入正弦波的频率，测得摩擦补偿后，关节速度环带宽为18 Hz，比补偿前提高了50%。由此可见，建立的摩擦补偿算法效果显著，能提高速度跟踪精度和速度环控制带宽，同时验证了摩擦模型辨识的准确性。

5 结 论

本文针对模块化关节，设计了摩擦模型的离线辨识方法和摩擦补偿算法。分别使用基于分段最小二乘法的一般辨识方法和基于灰狼算法的元启发式辨识方法对LuGre 摩擦模型进行了参数辨识，并对辨识结果进行对比分析。设计前馈摩擦补偿算法，以期望速度作为补偿器的输入，以补偿的电流值作为输出前馈给电流闭环。在模块化关节上进行实验，结果表明，相比于一般辨识方法，灰狼算法的辨识精度提高了19.2%；给定幅值为 1（°）/s，频率为 10 Hz 的速度正弦输入信号，摩擦补偿后，关节速度跟踪误差减小了38%；摩擦补偿后，速度环带宽提高了50%。所提出的参数辨识方法准确有效，摩擦补偿算法可以显著提高关节速度跟踪精度和速度环带宽。