α 和高斯混合噪声背景下超声波风矢量测量
石屹然,齐金伟,曲思凝,赵 洋
(吉林大学通信工程学院,吉林长春130022)
1 引 言
风速、风向作为气象要素的重要组成部分,在军事、航空、航海、交通等国计民生的各个方面均有着重大的影响[1]。相比于传统的如热敏测量[2]、多普勒测量[3]、皮托管测量[4]以及机械测量[5]等测量方法,超声波风矢量测量方法具有的测量精度高、范围宽、适用于各种野外复杂情况等优点,使之成为国内外学者的热点研究问题。
针对超声波风矢量测量问题,Ruttgen[6]提出了一种基于相对时差法的超声波风速风向测量方法,该方法利用超声波在顺、逆风情况下渡越时间的不同来测量风速,从而消除了环境温湿度等参数对测量精度的影响,有效地提高了测量精度。但是该方法忽略了环境噪声对超声波渡越时间测量的影响,在较低信噪比条件下,该方法测量性能急剧下降。对此,Castagnede 等[7]将超声波渡越时间测量问题凝练为含噪信号时延估计问题,提出了一种基于自相关时延参数估计的风矢量测量方法,有效抑制了高斯噪声对时延参数估计精度的影响。然而,该方法在一定程度上锐化了信号的峰值,存在峰值误判的问题[8]。Brassier 等[9]提出了一种基于互相关时延参数估计的超声波风矢量测量方法,该方法将发射信号与接收信号进行互相关运算,直接估计渡越时间,减小了计算结果的方差。曹长宏等[10]在互相关时延估计算法的基础上提出了一种二次互相关时延估计算法。该方法通过对互相关和自相关运算结果再次进行互相关运算以估计超声波渡越时间,进一步降低了时延估计算法的信噪比阈值。但是,基于时间延迟估计的超声波风矢量测量方法需在时间延迟为微秒级精度下进行,因而难以实现高精度、宽范围的测量[11]。
同时,在实际应用过程中发现,环境中不仅存在着高斯噪声,还存在着大量的具有脉冲冲击特性的非高斯噪声。研究结果表明[12][13],这种噪声在时域上表现出大量的脉冲尖峰特征,在频域上显示出更为厚重的拖尾现象。Nikias 指出[12],该类噪声可利用α 稳定分布过程进行表征。特别是当特征指数 α=2 时,α 稳定分布噪声(以下简称α 噪声)退变为传统高斯噪声。因此,高斯噪声是α 噪声的一个特例,α 噪声具有更为宽泛的适用范围。但是,α 稳定分布不存在有限的二阶矩,甚至当 α<1 时,连均值的运算都不能进行[13]。这直接导致传统的那些基于二阶矩或高阶累积量的超声波测量方法估计性能退化甚至失效。
针对上述问题,本文提出了一种基于分数低阶矩(Fractional Lower Order Moment,FLOM)的双相测量方法。首先,本文利用FLOM 算子对α 与高斯混合噪声进行抑制,提升了抑制噪声的能力;然后,将风矢量测量问题转化为相位估计问题,进而有效地扩大了算法的测量范围,利用参考信号的正交性提出了一种基于FLOM 的双相估计方法(以下简称分数低阶双相估计方法)。该方法可消除超声波信号传播过程中的幅度变化对相位估计的影响,同时实现了高精度、宽范围的风矢量测量。
2 模型建立
2.1 超声波测量模型
如图1 所示,分别在南北方向以及东西方向各布置一组超声波换能器,即S1,S2,W1,W2,其中S1 与S2,W1 与W2 之间距离相等,且同时具备收发功能,并采用相对时差法对风矢量进行测量。
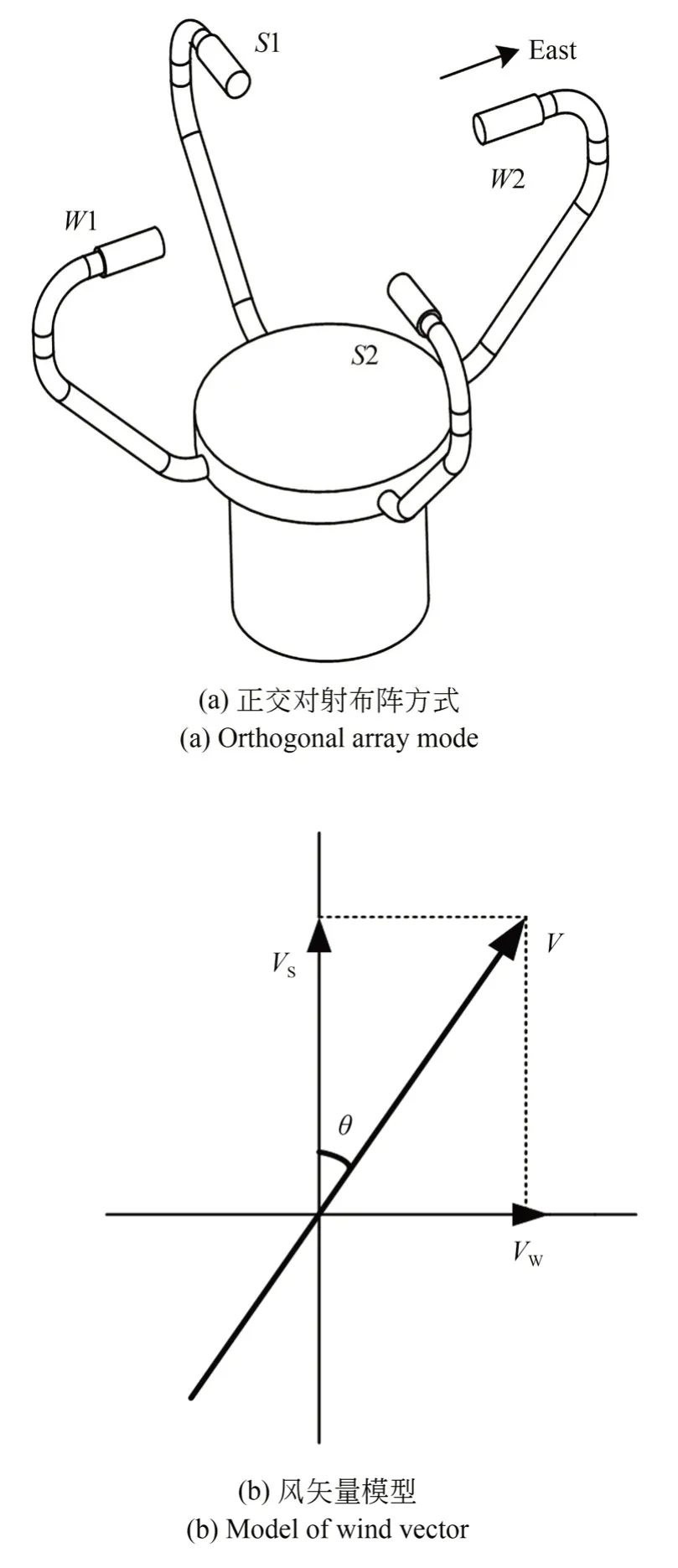
图1 风矢量测量模型Fig.1 Model of wind vector measurement
以东西方向为例,设由东到西(W2→W1)为顺风。当W2 发射超声波,W1 接收时,超声波在W2→W1 方向上传播的真实速度为:
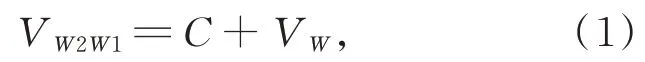
其中:C为声速,VW为风速在东西方向上的分量。
设W2 与W1 之间的距离为L,则超声波在W2→W1 方向上传播的时间为:
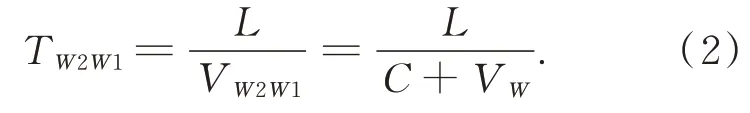
当W1 发射超声波,W2 接收时,超声波在W1→W2 方向上传播的真实速度为:
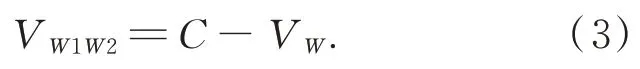
则超声波在W1→W2 方向上传播的时间为:
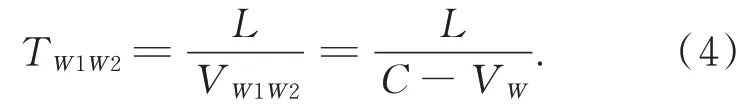
由式(2)与式(4)可求得风速在东西方向上分量为:
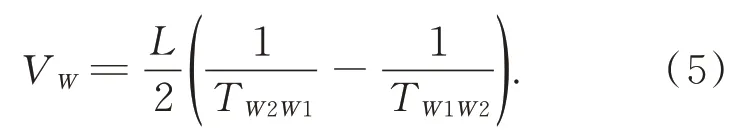
由式(5)可知,采用相对时差法可消除环境因素(温度、湿度等)对声速的影响。
同理,设由南到北(S2→S1)为顺风。则风速在南北方向上的速度分量为:
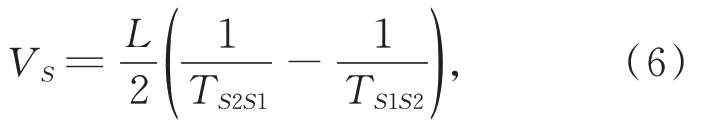
其中:TS2S1为超声波沿S2→S1 方向传播的时间,TS1S2为超声波沿S1→S2 方向传播的时间。
由于W1-W2 与S1-S2 之间正交,由式(5)与式(6)可得风速V与风向角θ分别为:
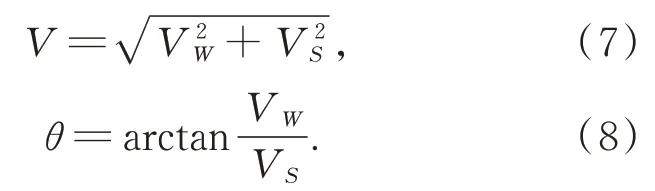
2.2 含噪信号模型
设超声波的发射信号为:
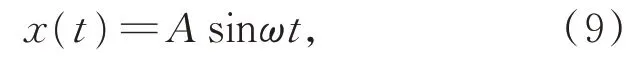
其中:A为参考信号的幅值,ω=2πf为参考信号的频率,f≥20 KHz 为中心频率。
设接收到的含噪超声信号y(t)为:
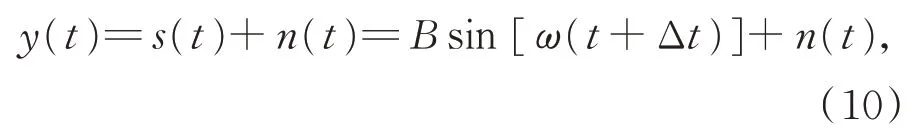
其中:s(t)为经过延迟的超声波信号,B为超声波传播后经过变化的幅值,Δt为超声波传播的延迟时间,n(t)为加性噪声。
不失一般性,假设噪声n(t)=nα(t)+ng(t),其中nα(t)服从α稳定分布,为 SαS 噪声,ng(t)为高斯白噪声,且ng(t),nα(t)与x(t),s(t)之间统计独立。
传统的基于时间延迟估计的超声波风矢量测量方法是通过直接估计超声波传播的延迟时间Δt来计算出风速与风向。
注意到,由于
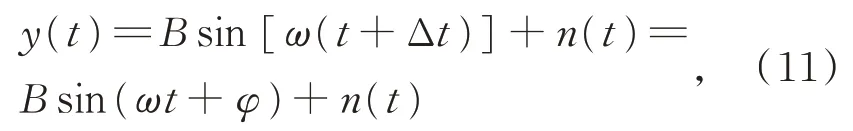
其中,φ=ωΔt为接收和发射超声信号的相位差。
因此,与传统的时间延迟估计方法相比,采用相位估计方法来估计φ等价于将Δt放大了ω倍,在相同的误差范围下,能够获得更高的估计精度,进而使得风矢量具有更高的测量精度和更宽的测量范围。
2.3 α 稳定分布
α稳定分布没有闭式的概率密度解析式,一般通过特征函数进行表征[14]:
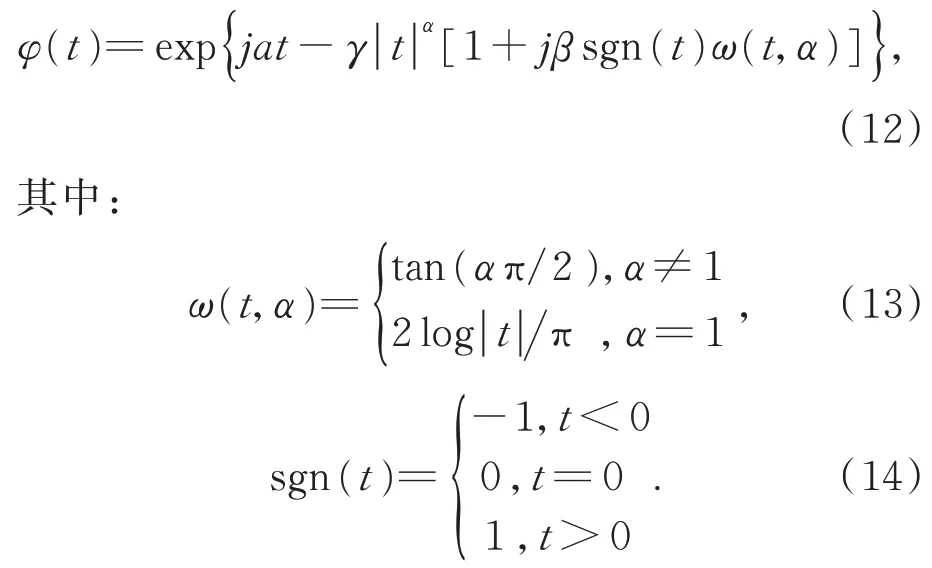
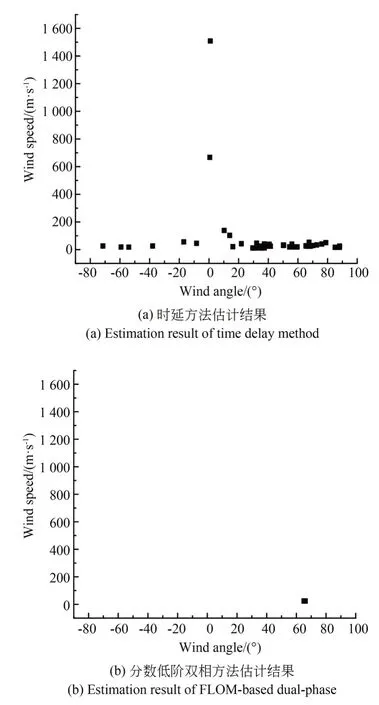
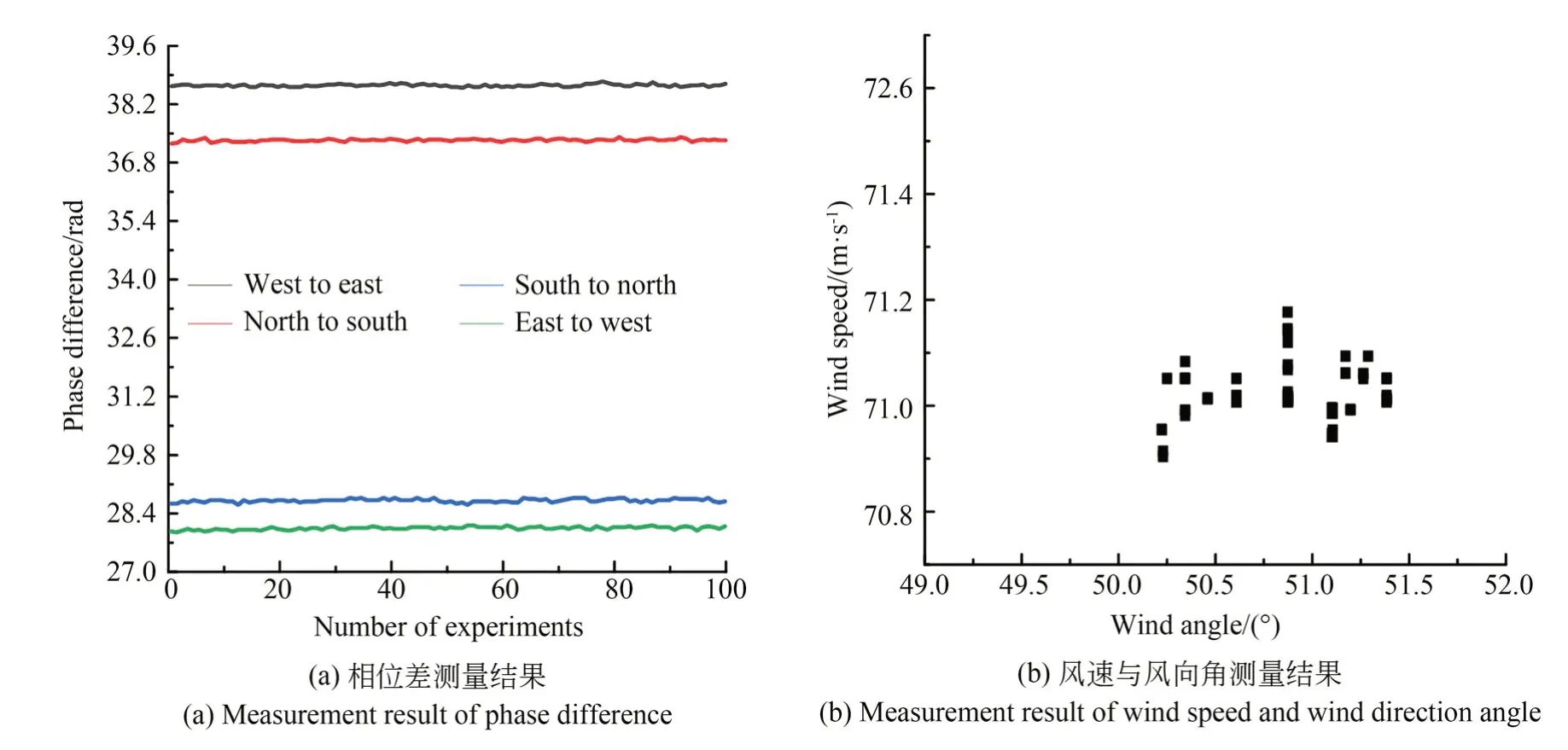
式(12)可记为:Sα(γ,β,a)。其中0<α≤2为特征指数,-1≤β≤ 1 为偏斜参数,γ≥ 0 为分散系数,-∞ 根据 FLOM 算子,由式(9)与式(11)可得超声波含噪信号的分数低阶互相关函数为[15]: 其中 0 将式(9)与式(11)代入式(15)可得: 由广义二项展开式可知[16],式(16)可转化为: 由前文假设,式(17)可以化简为: 由式(18)可知,利用 FLOM 算子,可将附加噪声n(t)充分抑制。为了获取超声波信号的相位差,将式(18)进一步化简可得: 在传统的相位估计方法中,均未考虑信号的幅值变化,即幅值A=B。然而,在超声波测量过程中,接收信号的幅值会受到传播路径、超声波换能器的性能等因素而发生变化,即幅值A≠B。如果仍认为A=B,在对φ进行估计时则会产生误差,进而对风速风向测量的精确性产生较大影响。因此,为了消除信号幅值变化带来的影响,本文在分数低阶互相关函数的基础上提出了分数低阶双相估计方法。 将式(9)的发射参考信号进行90°相移,可得 将式(20)与式(11)代入式(15)可得: 利用前文所述式(16)到式(19)的推导过程可得: 由式(22)与式(19)联立可得: 对比式(23)与式(19)可知,本文所提的分数低阶双相估计方法仅与相位差φ有关,有效的消除了超声波传播过程中幅值变化对相位估计的影响,极大提高了相位估计的精度。 为了确定式(24)中的n,以零风速条件为参考,由式(11)可得: 其中,φ0为零风速条件下的相位差。 设W1~W2 与S1~S2 方向上所测的最大风速为v,分别取顺风与逆风方向时,有: 其中,φv为最大风速条件下的相位差。 则式(25)与式(26)需满足如下条件: 化简式(27)可得: 由式(28)可知,在0~v风速段内满足条件的f,L可使所测得的相位差φ仅在φ0的 ±2π内波动,此时,相位差φ在式(24)中的n值与零风速条件下的n值相同,避免了因选取的超声波中心频率过高、换能器之间距离过长等因素引起的n值不确定的情况。其中,零风速条件下的n值可由式(25)确定,由式(24)与零风速下的n值即可确定φ。 由渡越时间与相位差关系式,风速在W1-W2 与S1-S2 方向上的分量分别为: 其中:φW2W1为W2→W1 方向上的相位差,φW1W2为W1→W2 方向上的相位差; 其中:φS2S1为S2→S1 方向上的相位差,φS1S2为S1→S2 方向上的相位差。 将式(29)与式(30)代入式(7)与式(8)即可计算出风速V与风向角θ。 实验1 验证分数低阶双相估计方法对α 与高斯混合噪声的抑制能力。 实验条件:超声波的中心频率f=25.0 KHz,幅度系数A=1,幅度系数B=0.6,超声波传播的距离L=0.07 m,声速C=340 m/s;附加噪声nα(t)为 SαS 噪声,它可按文献[17]产生,特征指数α=1.2,其信噪比采用如下广义信噪比定义: 取GSNR=2.5 dB。附加噪声ng(t)为高斯噪声,可根据文献[17]产生,其信噪比采用如下定义: 其中:PS为信号的有效功率,PN为噪声的有效功率。取SNg R=2.5 dB。FLOM 算子的阶次p=0.5,采样频率取10 MHz,数据长度取10 000。测量风速V=24.16 m s,风向角θ=65.56°。其中f,L,V,θ满足式(28)。 实验方法:使用本文方法与传统基于二阶矩的时延估计方法分别对风速以及风向角进行估计,进行100 次蒙特卡洛实验。其中基于二阶矩的时延估计方法可由文献[18]定义。 实验结果:图2 为基于二阶矩的时延估计方法和本文分数低阶双相估计方法在α与高斯混合噪声下超声波测风性能的仿真结果。 由图2 可知,由于α与高斯混合噪声的影响,传统的二阶矩时延估计方法将会在超声波进行风矢量测量时发生严重退化。而本文的分数低阶双相估计方法仍然能够较为准确地利用超声波进行风矢量的测量,所测得的风速的均方根误差为0.009 1,风向角的均方根误差为0.13。 图2 实验1 估计结果Fig.2 The estimation results of experiment 1 实验2 验证分数低阶双相估计方法的高精度测量性能。 实验条件:同实验1。 实验方法:使用本文方法与基于FLOM 的时延估计方法分别对风速以及风向角进行估计,进行100 次蒙特卡洛实验。其中基于FLOM 的时延估计方法可由文献[18]定义。 实验结果:图3 为基于FLOM 的时延估计方法和本文分数低阶双相估计方法在α与高斯混合噪声下超声波测风性能的仿真结果。 由图3 可知,在α与高斯混合噪声的影响下,基于分数低阶时延估计的超声波风矢量测量方法所测得的风速的均方根误差为0.027,风向角的均方根误差为0.361,本文方法所测得的风速的均方根误差为0.009 1,风向角的均方根误差为0.13。两种方法均具有较好的测量性能,但是本文分数低阶双相测量方法精确度更高。 图3 实验2 估计结果Fig.3 The estimation results of experiment 2 实验3 验证分数低阶双相估计方法的宽范围测量性能。 实验条件:在实验1 的基础上将测量风速提升到V=70.71 m s,风向角θ=45°。 实验方法:使用本文方法与基于FLOM 的时延估计方法分别对风速以及风向角进行估计,进行100 次蒙特卡洛实验。 实验结果:图4 为基于FLOM 的时延估计方法和本文分数低阶双相估计方法在α与高斯混合噪声下超声波测风性能的仿真结果。 图4 实验3 估计结果Fig.4 The estimation results of experiment 3 由图4 可知,在α 与高斯混合噪声的影响下,当测量风速提高到V=70.71 m s,风向角为θ=45°时,基于分数低阶时延估计的超声波风矢量测量方法已经失效,而本文的分数低阶双相测量方法仍然能够较为准确地利用超声波进行风矢量的测量,所测得的风速的均方根误差为0.083,风向角的均方根误差为0.363。 对比实验2 与实验3 可知,本文分数低阶双相估计方法较基于分数低阶时延估计的超声波风矢量测量方法的测量范围宽。 实验4 验证本文分数低阶双相估计方法在不同信噪比条件下的超声波测风性能。 实验条件:在实验1 条件下,使附加噪声的信噪比SNR=GSNR+SNg R以5 dB 间隔从-10 dB 到 10 dB 增加。 实验方法:在每一信噪比下,采用本文分数低阶双相估计方法进行100 次蒙特卡洛实验。将实验的结果进行均方根误差(RMSE)[19]运算: 其中:Vr为真实风速,θr为真实风向角。 实验结果:图5 为在不同信噪比下,采用本文分数低阶双相估计方法进行超声波风矢量得到的风速与风向角的均方根误差曲线。 图5 风速与风向角的均方根误差曲线Fig.5 RMSE curve of wind speed and wind direction angle 由图5 可知,随着α 与高斯混合噪声信噪比(SNR)的逐渐增大,测得的风速与风向角的均方根误差(RMSE)逐渐减小。即使在SNR=-10 dB 的条件下,本文方法在进行超声波风矢量测量时仍有很高的精度,充分体现了本文方法对高斯与α 混合噪声的强抑制能力。 将本文方法应用在超声波风矢量测量实验台上进行测试,实验平台如图6 所示。 图6 超声波测风平台Fig.6 Ultrasonic wind measuring platform 实验方法:在长春气象所EDE1-5 型风洞中,在风速V=71.06 m s,风向角θ=50.71°的环境下进行测试。其中L=0.07 m,f=25.0 KHz。采用在测量环境周围放置多个交流接触器,使其进行反复开关动作产生高斯与α混合噪声。 实验结果:图7 为在超声波风矢量实测平台所得的实验结果。 图7 风矢量实测图Fig.7 Actual wind vector test map 由图7 可知,在α与高斯混合噪声的干扰下,采用本文分数低阶双相估计方法所测得的均方根误差为0.104,风向角的均方根误差为0.54。可见本文提出的分数低阶双相估计方法在实物平台实测风矢量时具有较强的泛化能力。 本文针对α 与高斯混合噪声下超声波风矢量测量问题,首先利用FLOM 算子对α与高斯混合噪声进行抑制,弥补了传统的二阶矩和高阶累积量方法在超声波风矢量测量中退化失效的不足。然后在此基础上,将时延估计方法转化为相位估计方法,并利用参考信号的正交性,提出了一种分数低阶双相估计方法,解决了超声波传播过程中的幅值变化降低风矢量测量精度的问题,有效地扩大了风矢量的测量范围。仿真与实测结果表明: (1)与传统的二阶矩时延估计方法相比,分数低阶双相测量方法对高斯与α混合噪声具有强抑制能力。与基于FLOM 的时延估计方法相比,分数低阶双相测量方法在中低风速段具有更高的精度,而在高风速段,基于FLOM 的时延估计方法已经失效,但是分数低阶双相测量方法仍然具有良好的测风能力。 (2)在信噪比为-10 dB 的条件下,风速的均方根误差小于1.5 m/s,风向角的均方根误差小于2°,仍然具有较高的精度。 (3)在实测平台上,本文方法在风速V=70.71 m s,风向角θ=45°的环境下所测得的风速的均方根误差为0.104,风向角的均方根误差为0.54,具有较强的泛化能力。3 基于分数低阶双相估计方法的超声波风矢量测量
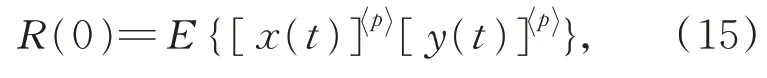
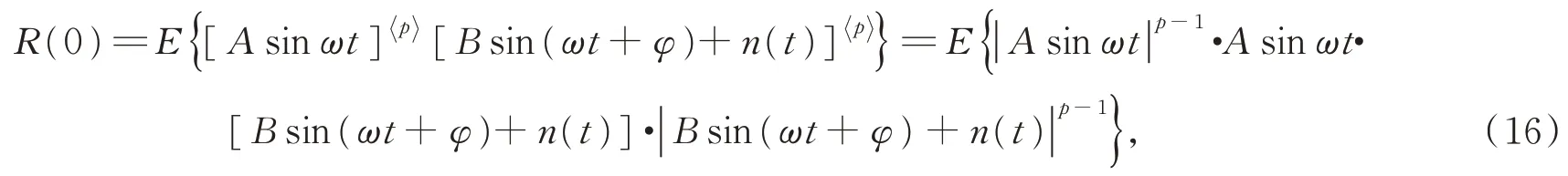
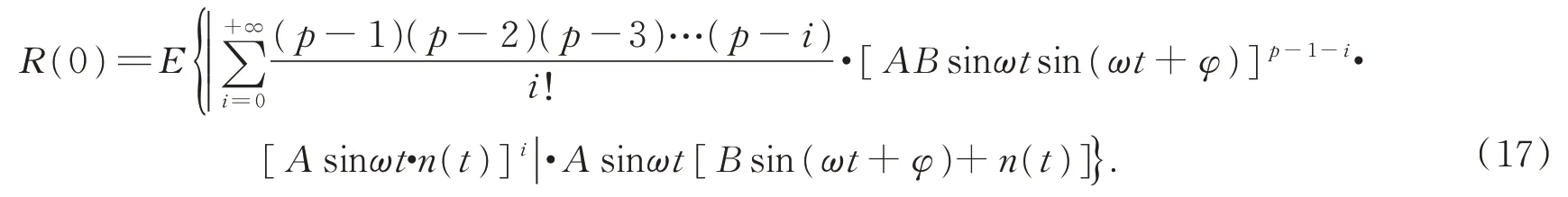
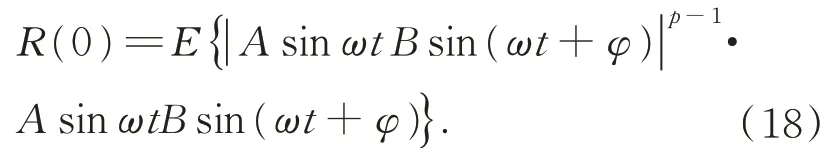
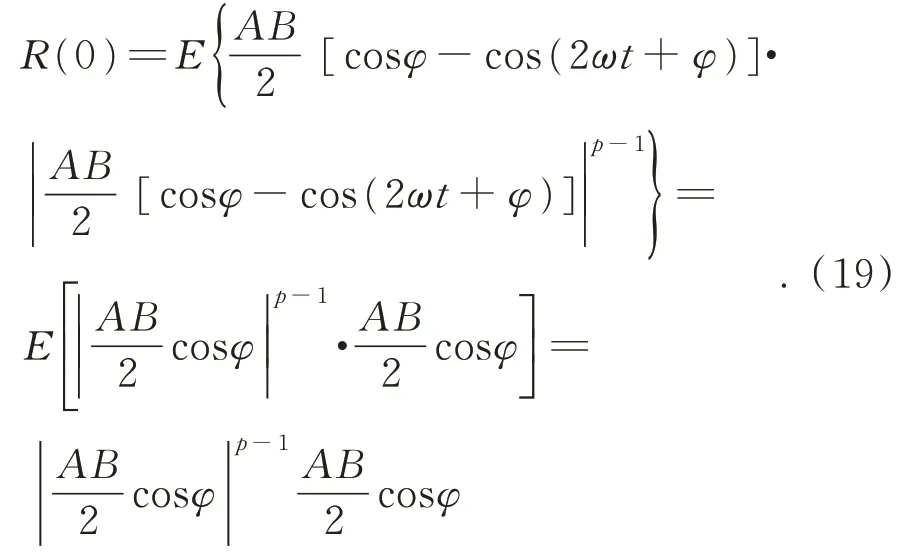
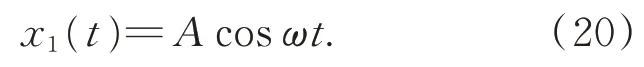
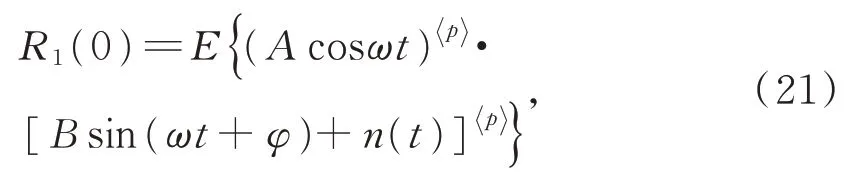
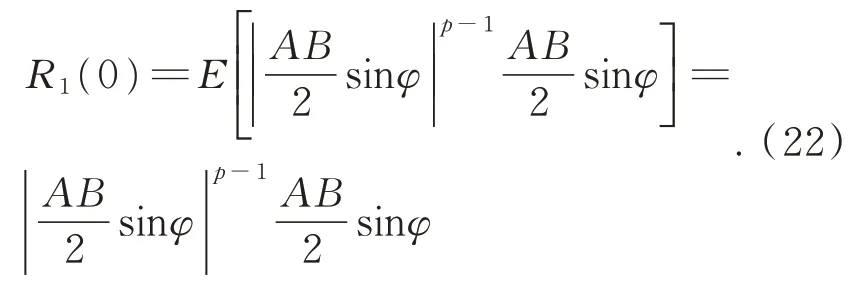
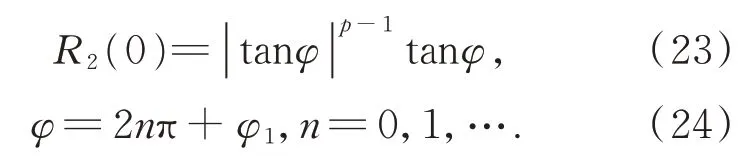


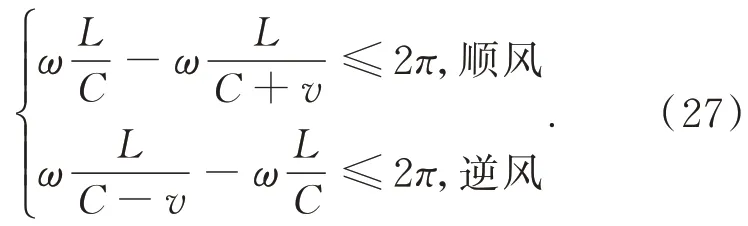
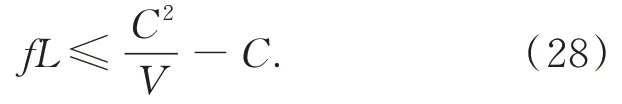
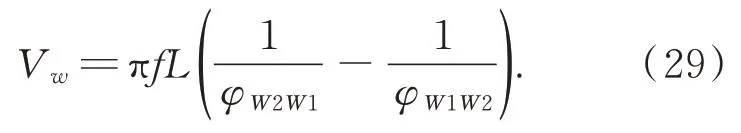
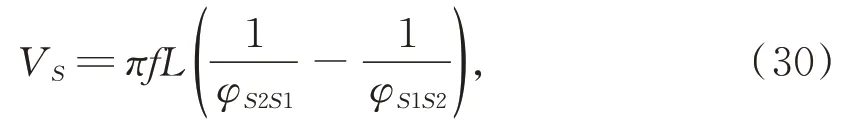
4 仿真分析与实际测试
4.1 仿真分析
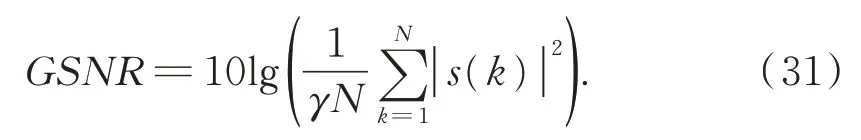
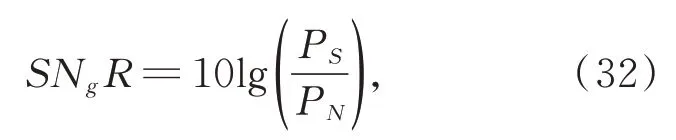
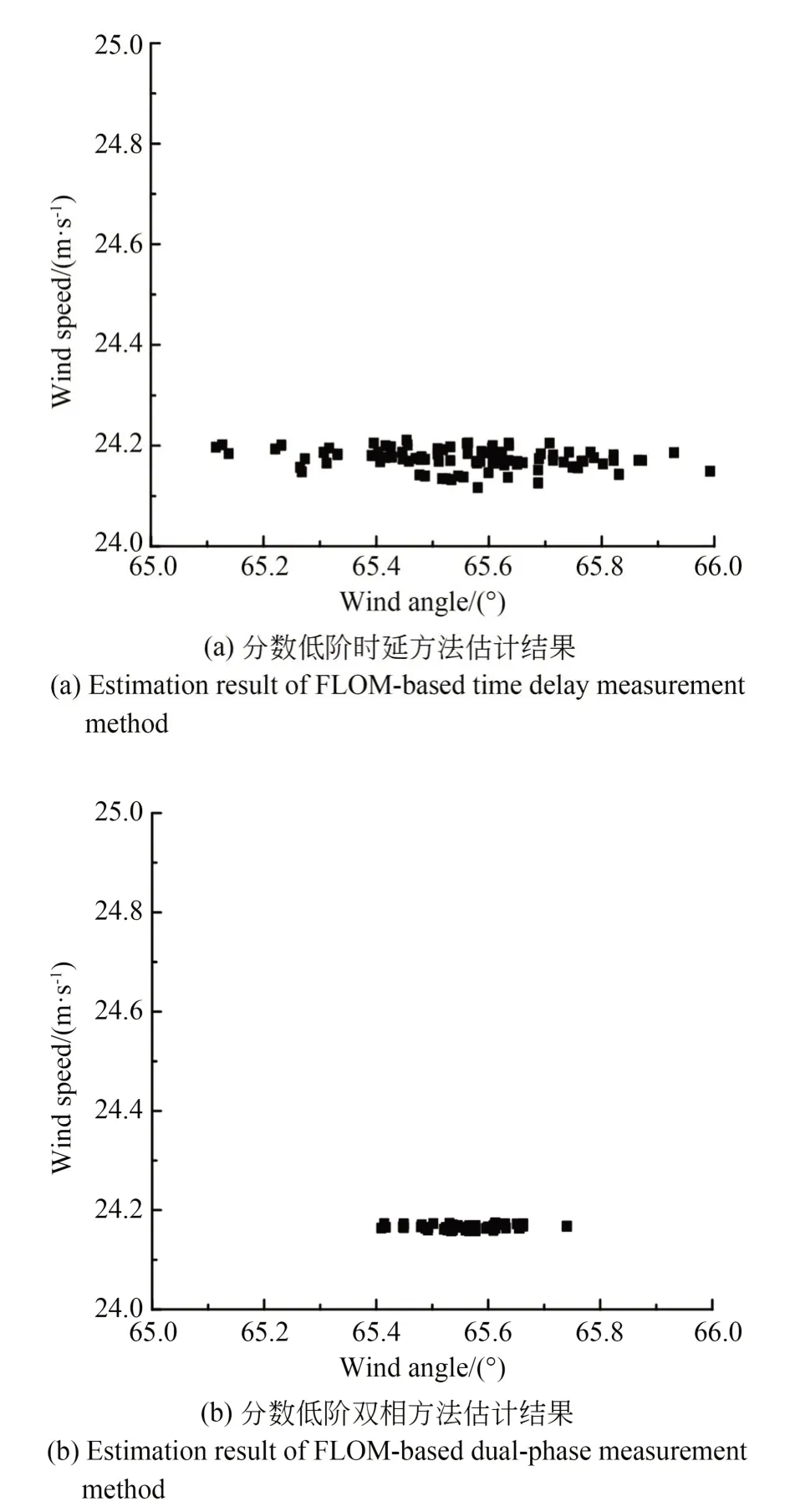
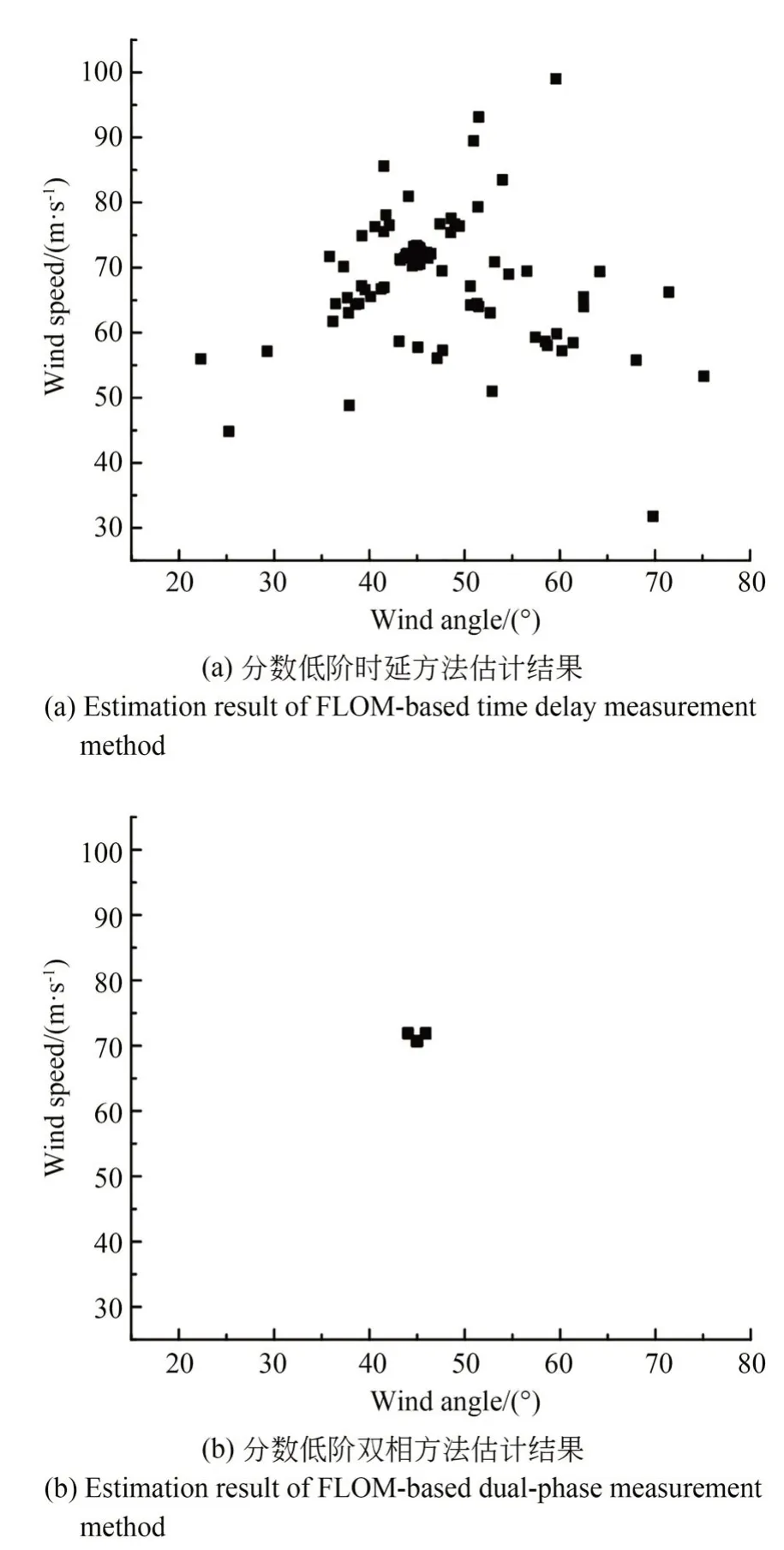
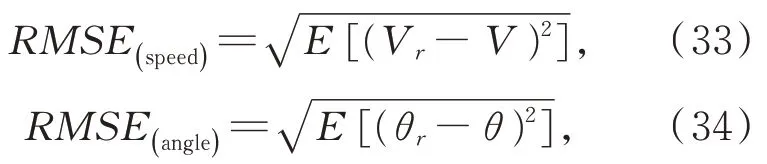
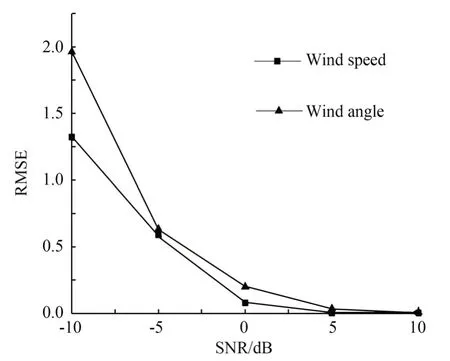
4.2 实际测试

5 结 论

