结构健康监测系统光纤Bragg 光栅应变计的异常诊断
孙 晓,王清梅,李振伟,楚敬敬
(1. 青岛科技大学自动化与电子工程学院,山东青岛266061;2. 中科院国家天文台,北京 100012)
1 引 言
为确保结构的安全可靠,结构健康监测技术[1]广泛应用于土木工程结构、钢结构等大型工程中,通过布设各类传感器,监测并评估结构的健康状态。光纤布拉格光栅(Fiber Bragg Grat⁃ing,FBG)应变计是一种光纤传感器[2],它利用光纤的光敏性在纤芯上建立折射率调制,光栅的周期和折射率随安装点的温度和应变变化,引起反射光波长的变化,通过测量反射光波长的变化,来测量目标的应变信息。FBG 因其光信号稳定,单根光纤可串联多个光栅测点[3],不受电磁干扰,适合分布传感等特点[4],大量应用在工程结构的应变监测中。
500 米口径球形射电望远镜(Five-hundredmeter Aperture Spherical Telescope,FAST)为具有主动反射面的球冠状大型射电望远镜[5]。主动反射面系统结构特殊且空间跨度大,为保证主动反射面可靠工作,建设了一套主动反射面健康监测系统[6],用于反射面的故障诊断与预警。其中,用于索力监测及圈梁钢结构监测的FBG 应变计共计416 个。这些传感器长期工作于复杂的室外环境中,易发生安装失效、蠕变、漂移、老化和线路故障等问题,使其监测数据错误或失效。传感器故障会直接影响健康监测系统的性能,必须进行及时的检查与维护,识别并排除异常,保证数据的可靠性。如果采用人工巡检排查的方法,不仅工作量大,而且许多传感器的安装位置不具备人工观察的条件,无法及时有效地发现与维护故障测点,从而形成安全隐患。
国内外学者针对FBG 传感器的异常诊断展开了研究。Cazzulani[7]等基于测量估计残差的分析,识别FBG 传感器链中不同的故障类型,排除故障传感器数据。张晓丽[8]等借助光波导数值分析软件对FBG 传感器性能退化的信号特征进行了分析,为FBG 传感器的自诊断提供依据。姜婷睿[9]等利用小波包和主元分析结合提取船用FBG 应变计故障特征,实现了故障的基本诊断。传感器异常自诊断可有效提高传感器的工作效率与可靠性,不同传感器的异常诊断方法存在共通性[10],广泛应用于机电[11]、驱动控制[12]、航空航天发动机[13]以及数据采集等系统中。
传感器的异常诊断方法主要有基于模型、基于知识和基于信号处理方法等[14]。基于模型的方法需获得系统的精确解析模型,且系统的非线性及不确定性会对诊断结果产生很大影响;基于知识的方法需有足够的故障原因与特征的先验知识积累转化为推理规则;基于信号处理的方法只需对传感器的信号特性进行分析,不需建立精确的模型或足够的先验知识,利用信号特性结合主成分分析、人工神经网络等算法就可完成对传感器的故障诊断[15]。鉴于此,本文基于信号处理方法,利用结构健康监测中FBG 应变计的信号特征进行异常诊断。
2 原 理
2.1 光纤光栅应变计原理
FBG 应变计的原始输出信号为光栅反射中心波长,当光栅外界应力或温度变化时,反射中心波长随之变化,输出波长为:
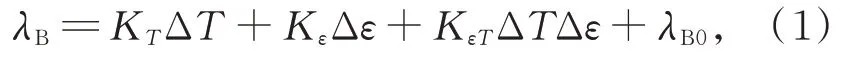
式中:KT为光栅温度灵敏系数,Kε为光栅应变灵敏系数,ΔT为光栅温度变化值,Δε为光栅处应变变化值,λB0为中心波长的初始值,KεT为光栅温度应变交叉敏感系数。可见FBG 应变计的原始输出信号易受温度影响,在实际应用中常采取相应措施,补偿温度变化对应变的影响[16]。
2.2 异常诊断原理
FAST 的主动反射面为索网结构,主索网与支承钢结构的圈梁应力变化存在传递性。在主动反射面不变形期间,结构应力发生变化的主要原因为环境荷载,FBG 应变计所承受的主要周期荷载为温度荷载。所有应变计测点的工作环境及监测对象承受的荷载变化规律大致相同。分析发现,正常FBG 应变计测点输出信号,其波形幅值等存在相似性,统计不同传感器的多种特征值,其数据分布呈聚合状态。传感器故障会导致信号特征发生变化,如表1 所示。所以,基于传感器测点历史数据,提取每个测点的关键特征值,利用其数据分布规律寻找特征值偏差较大的离群测点,可对所有FBG 传感器进行自动化异常诊断。
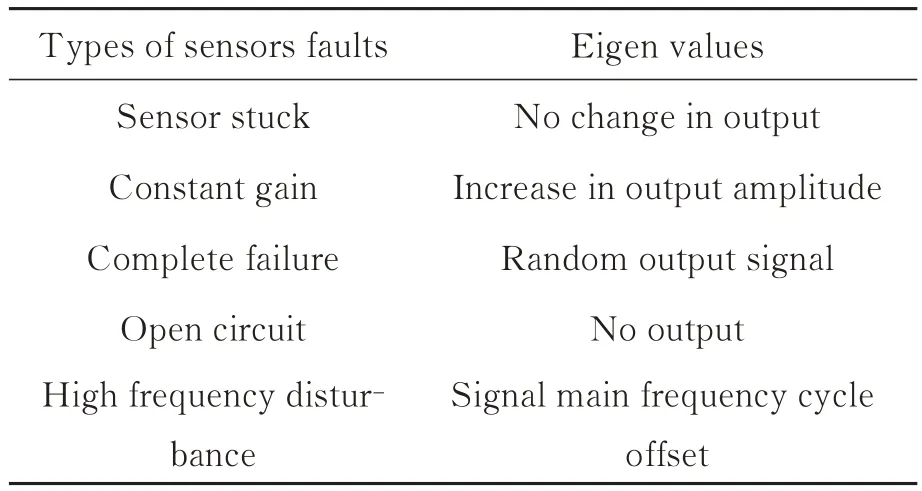
表1 传感器故障与特征变化Tab.1 Failure types and characteristic change of sensors
3 数据预处理
FAST 主动反射面健康监测系统传感器的数据特点如下:(1)时间上存在断层,FAST 对电磁环境极为敏感,健康监测系统在工作过程中并非持续监测;(2)部分测点数据缺失,由于软件设置或者硬件设备的检修,部分传感器数据通道被关闭,需加以筛选;(3)数据量大,采样周期为1 s,单测点每月数据可达250 多万条,附带传感器其他信息,单测点每月数据可达200 MB 以上。在进行故障特征提取时,需对数据库内的历史数据进行预处理。
3.1 数据抽取
根据传感器的编号及标识符,循环读取健康监测系统中单测点规定时间周期内的历史数据。由于传感器的主要荷载为温度荷载,其变化周期以天为单位。为丰富信号特征,抽取7 天左右的历史数据,去除与诊断无关的信息,仅保留诊断所需的原始波长信号,作为原始样本λ(n),如图1所示。
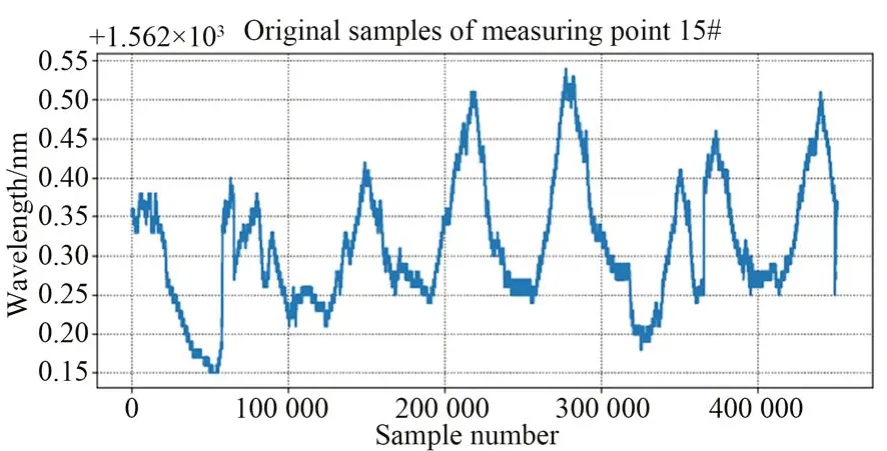
图1 测点输出原始信号样本示例Fig.1 Original samples of measuring point example
3.2 压缩滤波
根据FAST 的运行特点,结构主要荷载的变化周期较长,为压缩样本数据量,便于转换与计算,对原始样本进行采样压缩,压缩采样周期选为1 000 s,满足采样定理的要求。再对数据低通滤波,滤除高次谐波的干扰,压缩采样公式为:
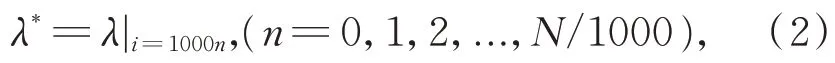
式中:N为原始样本长度,压缩样本长度为N/1 000。采用三阶低通数字滤波器滤波,滤波公式为:
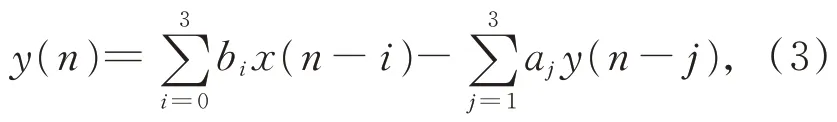
式中:bi,aj为滤波器系数,x为输入信号,y为输出信号。压缩并滤波后的数据作为压缩样本λ*(m),示例如图 2 所示。
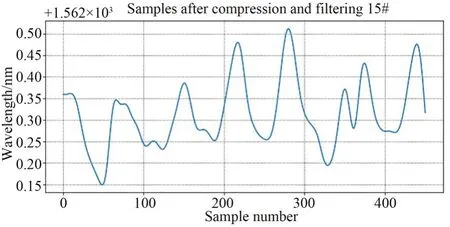
图2 压缩采样后信号示例Fig.2 Samples after compression and filtering of measur⁃ing point example
4 特征提取
正常FBG 应变计近似的信号统计指标主要有信号长度、标准差、时域能量值、频域主成分周期、幅值、方差、波形、峰值和脉冲等。这些指标的实质评价作用存在重复,经分析选择前4 项作为特征进行诊断。
4.1 原始样本长度
FAST 健康监测系统软件采集数据时,测量数值波动超过一定阈值则会舍弃,所以部分异常测点的数据表现为大量缺失。软件错误,偶发故障等原因,也会造成数据缺失。按时间段抽取数据,每个测点所得的样本长度不一致,所以测点最终读取的样本长度是评判传感器状态的重要特征之一。样本长度特征记为:
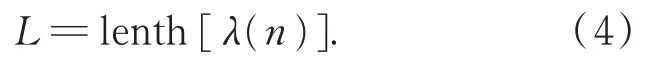
4.2 原始样本标准差
测点信号标准差能反映一个数据集的离散程度,可作为评判测点信号稳定程度的依据。为保留更多有效信息,使用测点原始样本,计算公式为:
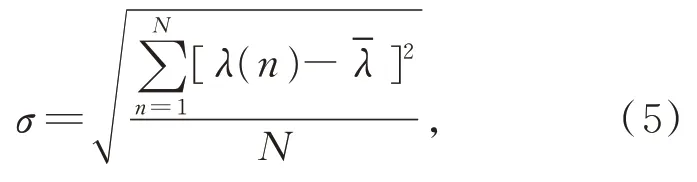
4.3 压缩样本时域能量值
时域能量值反映测点输出信号的波动强度,对输出幅值无明显变化或者增益过大有较强的指示作用。为避免异常值干扰,使用压缩样本,先对数据去均值化,再计算该测点能量值,计算公式为:
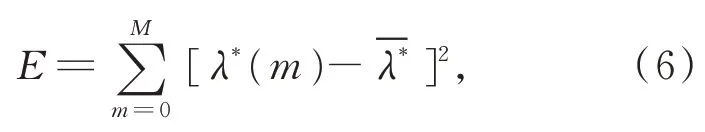
式中:M=N/1 000 取正整数,为压缩滤波后样本数据的长度为压缩样本平均值。
4.4 信号频域主成分周期
在FAST 健康监测系统中,造成结构应力变化较大的主要荷载是环境温度。正常FBG 应变计输出的原始波长信号的主要荷载成分受温度影响,波动周期在一天左右。计算信号频谱,获取频域信号的最大峰值,由它对应频率换算得信号频域主成分周期,可作为信号周期特征是否正常的评价依据。
使用压缩样本,先对数据去均值化,信号频谱函数的计算公式为:
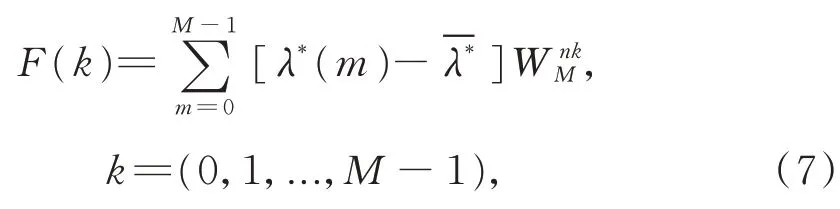
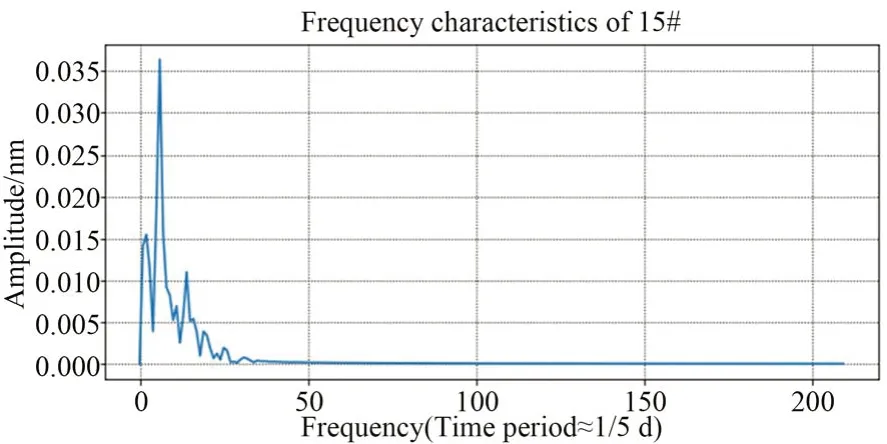
图3 压缩信号频谱示例Fig.3 Frequency characteristics example of compressed signal
提取峰值对应的频率fmax,换算频域主成分对应的周期特征值,为使数据更直观,换算单位为小时:
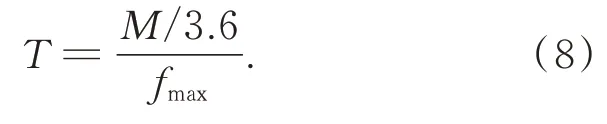
循环提取所有测点特征值,若有K个测点正常提取到数据并存在特征值,可得特征值列表为:
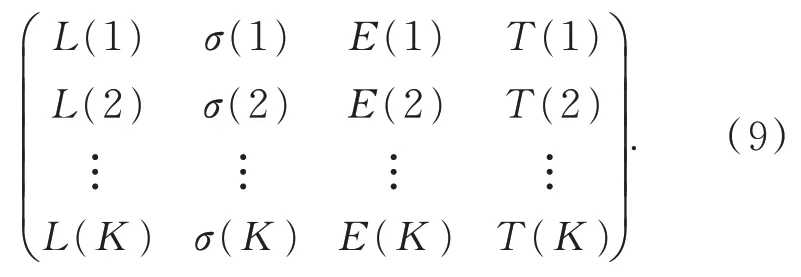
5 异常诊断
5.1 诊断方法
分析式(9)可知,正常传感器的特征值在数据上较为接近,呈聚合状态,而异常或故障传感器则呈离群状态。为识别测点对应特征的离群程度,评判传感器的异常状态,需获取特征值中心点。
5.1.1 获取聚合中心点
为避免离群过大的数值对特征中心的影响,中心点不使用数据均值,而是采用循环迭代的方式搜寻附近聚合点数最多的测点特征值作为一维数据的聚合中心点。以样本长度特征为例,定义数据收敛系数为:
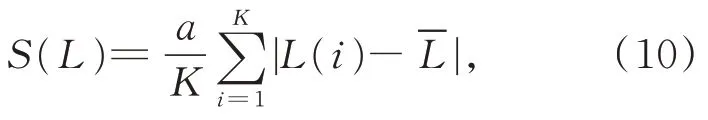
式中:a为收敛系数倍数,可通过调节a来调节判断靠近聚合点的距离,取值在0.5~1.5 为佳,此处a取0.5;K为特征值列表长度。
两点之间的欧式距离为:
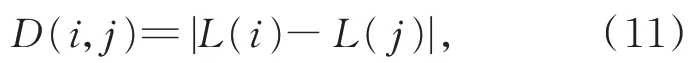
式中i,j为两不同测点序号。
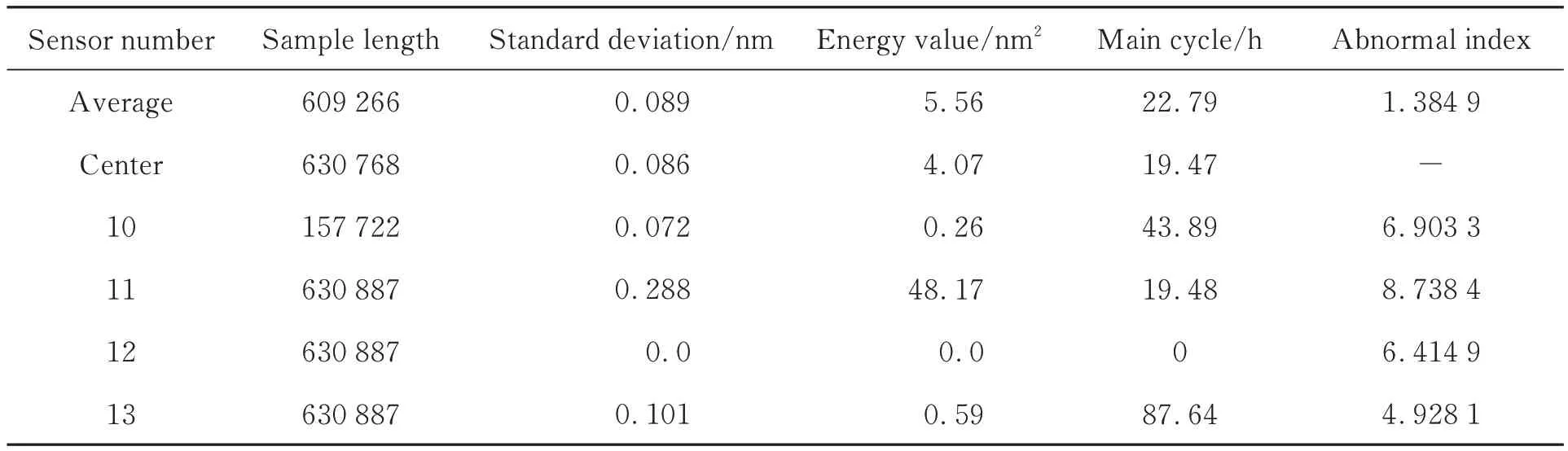
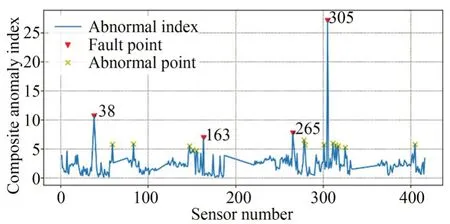
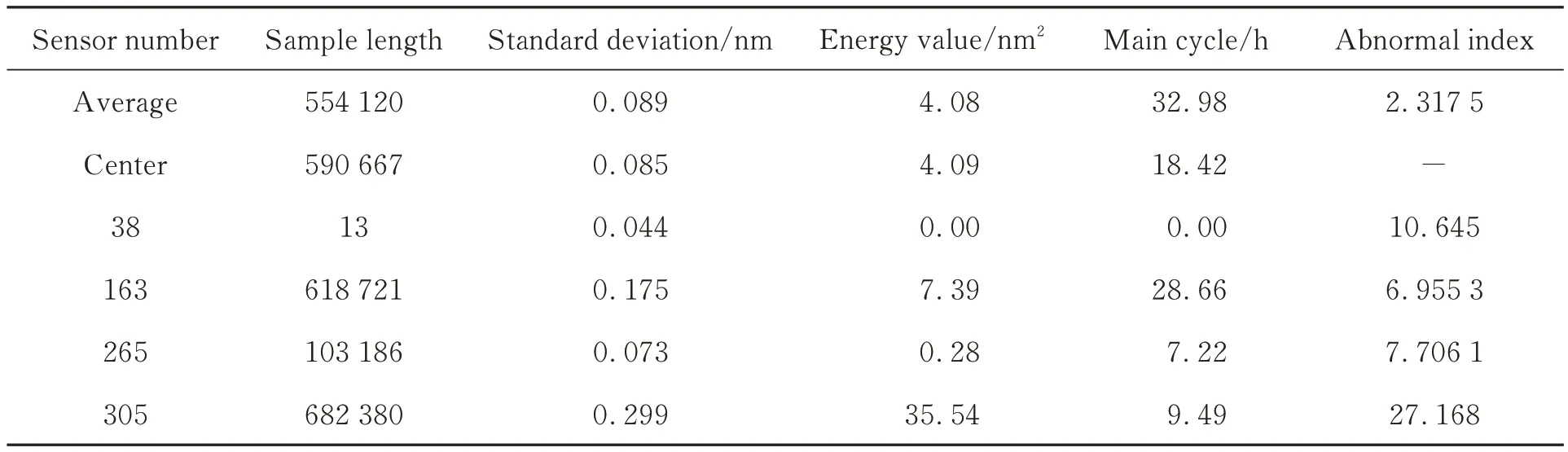
若D(i,j) 图4 循环迭代流程Fig.4 Flow chart of loop iteration 数组num 中最大值,即附近聚合点数最多的数据点,对应脚标imax所对应特征值L(imax)作为中心点数值,记作L(center)。若有多个数据点聚合数目均为相等最大值,则取这多个数据点对应特征值的均值,作为特征值中心点。同理,可获取其他三个特征值的中心点,得[L(center),σ(center),E(center),T(center)]。 5.1.2 传感器综合异常指数 离群程度评价的目的是使传感器每类特征具备同等权重,避免因为特征值本身数量级差别造成的影响。计算特征离群程度时,引入Z-score思想对偏离距离进行标准化,每个特征向量标准差记作: 定义传感器综合异常指数为: 式中:i=1,2,…,K,为测点编号。 当传感器发生卡死时,输出恒定不变,提取主成分周期结果为空值,进一步处理时需将空值替换为 0,且将d(i)+3 作为故障标记。 式中:k1,k2为故障系数与异常系数,1 取FAST 健康监测系统中FBG 传感器2019年7 月份1~9 号测点作为正常传感器样本,并模拟几种传感器的故障数据作为故障样本。 5.2.1 传感器数据大量缺失 对3 号测点数据进行采样压缩,压缩4 倍,作为模拟10 号测点,得到: 5.2.2 传感器恒增益 测量信号呈倍数增长,对3 号测点数据的输出幅值进行放大,增益4 倍,作为模拟11 号测点,公式为: 5.2.3 传感器卡死 传感器卡死表现为输出为某一固定值叠加微弱的噪声信号。实际情况中,由于传感器本身精度原因,以及采集系统在数据记录时预处理,微弱噪声往往已被消除,且本方法会进行去均值处理。采用与3 号测点同长度的数据,每个数据点替换为0,作为模拟12 号测点。 5.2.4 输出信号随机 使用生成的随机数据与3 号测点幅值的乘积作为模拟数据,作为模拟13 号测点。 故障测点4 个,正常测点9 个,为增加正常测点比例,将测点1~9 号数据重复一次,作为14~22 号测点。使用诊断方法对仿真模拟数据进行诊断,诊断结果如图5 所示,特征值与异常指数见表2。测试证明,当故障测点占总测点数量的20%以内时,可有效识别故障传感器。异常测点过多,会导致特征值分布过于离散,诊断效果不佳,此时需调整故障和异常系数,进一步严格指数偏离程度。仿真结果显示,当故障测点比例每增加 10%,故障系数k1大约减少(k1-1)/2,如故障测点占比30%时k1调整为2,40%时k1调整为1.5,异常系数仍选择中值;当故障测点比例占50%时,故障系数低至1.1,此时传感器故障过半,正常传感器与异常传感器界定不明显,方法无法诊断。 图5 仿真实验结果Fig.5 Simulation experiment results 表2 仿真传感器的特征及异常指数Tab.2 Eigen values and abnormal indexes of simulated sensors 以FAST 健康监测系统2019 年7 月份的FBG 应变计数据为样本,根据FAST 的观测需求,健康监测系统的实际工作时间约为7 天,数据长度满足方法诊断需求。遍历416 个传感器数据库,共成功提取317 个测点对应特征值,异常诊断结果如图6 所示,特征值与异常指数见表3。 图6 传感器异常诊断结果Fig.6 Result of sensor abnormal diagnosis 表3 故障传感器的特征及异常指数Tab.3 Eigen values and abnormal indexes of fault sensors 诊断共识别出4 个故障测点与14 个异常测点。人工对故障与异常测点进行核查,缺失的99个测点未获取数据的原因为光纤光栅解调仪设备离线检修,无监测数据。故障测点中,38 与265号测点因大量传感器数据返回错误被丢弃,传感器数据长度远低于正常水平。163 与305 号测点为数据存在大量跳变,引起多项特征离群,其中305 号测点更为严重。14 个异常测点的主要问题为监测信号中存在较强的高频信号干扰,明显异于其他正常传感器的平滑信号。 由此可见,诊断结果对传感器的工作状态有较强的指示作用,可根据诊断结果对故障传感器通道进行关闭并维修,防止错误数据影响健康监测系统的监控功能。而对异常传感器,需进行进一步排查,例如高频干扰,多由测点附近的机械振动或光纤通道干扰造成,应及时排除,防止传感器状态进一步恶化。 本文基于健康监测系统中光纤光栅应变计原始输出波长信号具有统一规律的原理,使用信号处理的方法提取历史数据中心反映传感器状态的特征值,建立特征列表。通过循环迭代寻找一维特征值的聚合中心,并根据特征值的离群程度定义综合异常指数,实现了传感器的故障与异常诊断。仿真结果表明,当故障测点占总测点数量的20%以内时,可有效识别故障;当异常测点过多致使特征值过于离散时,可进一步调节异常与故障系数。利用FAST 健康监测系统2019 年9 月份的数据对416 个FBG 传感器进行了诊断,共识别出4 个故障测点,14 个异常测点,人工核查无误。 该方法是一种自动化的传感器异常诊断方法,不需要大量先验知识的训练,根据传感器的历史数据对传感器状态进行评估,对多种故障有较强的指示作用。它能够及时、自动化地识别故障传感器测点,节省大量人力,提高系统可靠性。不过,传感器的具体故障与异常原因仍需结合人工核查,在故障类别的自动判别上存在不足,需进一步研究。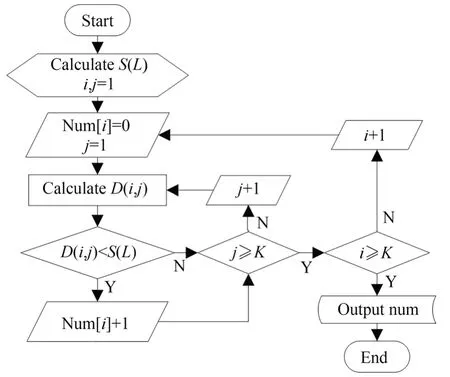
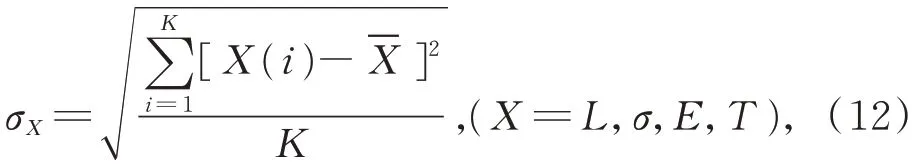
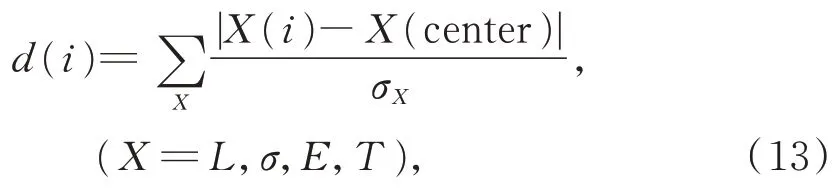
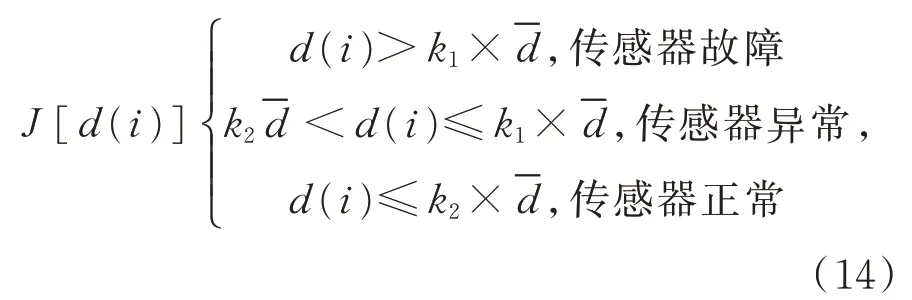
5.2 仿真验证
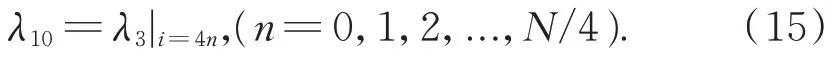
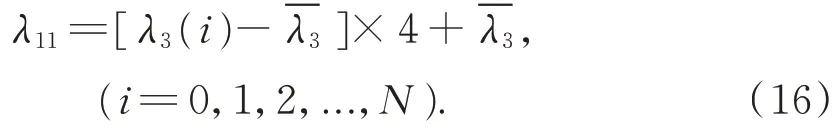
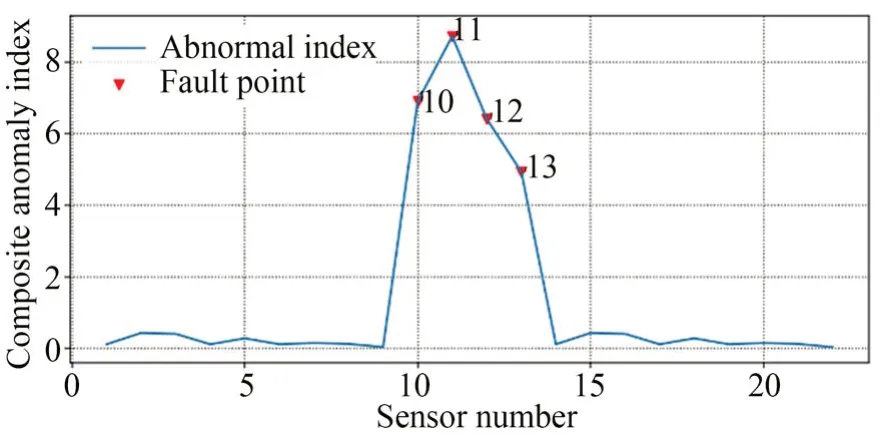
5.3 实际应用
6 结 论

