利用深度学习扩展非接触扩散光学层析成像系统中探测器的动态范围

赵 星，刘桐君，陈 平，王京凡，刘伟伟，2

（1. 南开大学 现代光学研究所，天津 300350；2. 天津市微尺度光学信息技术科学重点实验室，天津300350）

1 引 言

扩散光学层析成像（Diffuse Optical Tomog⁃raphy，DOT）［1］是一种能够快速无损探测组织吸收散射系数分布的技术，被广泛应用于脑功能成像［2-3］，乳腺癌诊断［4-5］，关节成像［6-7］，农产品质量检测［8］等领域。其本质是求解一个包含光子传输模型的逆问题，具有内在的非线性及病态性［9］。而获取更多的信息用于重建能够有效地提高DOT 重建图像的空间分辨率和对比度，并消除伪影。高密度DOT 系统是最直接的方案，如Eggebrecht 等人［2］在 2014 年搭建的接触式高密度DOT 系统，该系统对人脑部进行功能成像并和功能核磁共振进行对比，展示了高密度DOT 系统的有效性与准确性。虽然该系统具有很高的准确率，但系统组件非常多且复杂。非接触式DOT 系统则能有效克服这个问题，其光源和探测器不再以光纤探头的方式接触式地分布于组织表面，光源是直接在空间中传输的激光束，探测器则使用EM-CCD［10-11］等面成像装置，特点是能够一次性大面积地采集组织表面的能流分布。Takamasa［12］等人使用纳秒级脉冲激光和时间提取的图像传感器制作了非接触式时域高密度DOT 系统，该系统无需使用密集的光纤探头就可以轻松获取高密度测量点。使用这套系统分别对模拟头部吸收系数的仿体和真人的脑部进行了测量，研究了人脑在完成简单计算任务时的活动情况。当然该系统也存在着限制，探测到的部分光信号会被具有较高吸收系数和散射系数的组织或介质衰减，这意味着随着探测范围的加大，光的衰减将进一步加强，数据的动态范围也进一步变大。因此，在已有的非接触式DOT 系统中，为了获得足够精确的探测数据，一般采用调整硬件参数的方法，如选择较小尺寸或较小吸收系数的探测目标以减小对探测器动态范围的需求，或选择使用较为昂贵的高动态范围CCD来满足探测需要。虽然这些方法保证了测量精度，但却限制了非接触DOT 系统的应用空间及前景。使用算法修复有误差的数据则能够在保证DOT 重建精度的同时，降低非接触DOT 系统对于探测器动态范围的需求。

深度学习是机器学习的一种，适用于拥有大量数据的非线性问题的建模，已经应用在图像分辨率增强［13］、模糊图像恢复［14］、光纤传输后散斑恢复［15］、高光谱分类［16］和遥感图像检索［17］等领域，并展示了非常强的数据恢复能力和建模能力。本文采用深度学习的方法，使用可进行DOT 计算和重建的NIRFAST 开源程序对不同二维吸收散射特性的介质进行计算，通过数据截断方法模拟低动态范围探测器的信号获取过程，生成大量训练样本。在此基础上搭建了一维全连接网络并完成了模型训练，最后，通过仿真和实验方法对模型的性能进行了分析及验证。该方法能够有效地修复受探测器动态范围限制而获得的误差较大的探测数据，并成功重建出介质中吸收系数的分布特性。

2 基本原理

2.1 DOT 简介及重建算法

DOT 是一种利用光通过吸收散射介质表面能流密度分布和光子传输模型计算重建介质内部吸收系数和散射系数分布的技术。其基本的测量过程示意图如图1 所示。图中的介质具有一定的吸收散射特性，介质上表面的点表示光源的入射位置，下表面的点表示探测位置。当光依次从介质上表面的光源位置入射时，进入介质的光发生吸收及多次散射，最后从介质下表面出射。利用点探测器或面探测器探测从介质下表面出射的扩散光的能流密度，在得到各探测位置的一组数据后，利用DOT 求解算法即可计算重建介质内部的吸收系数分布。

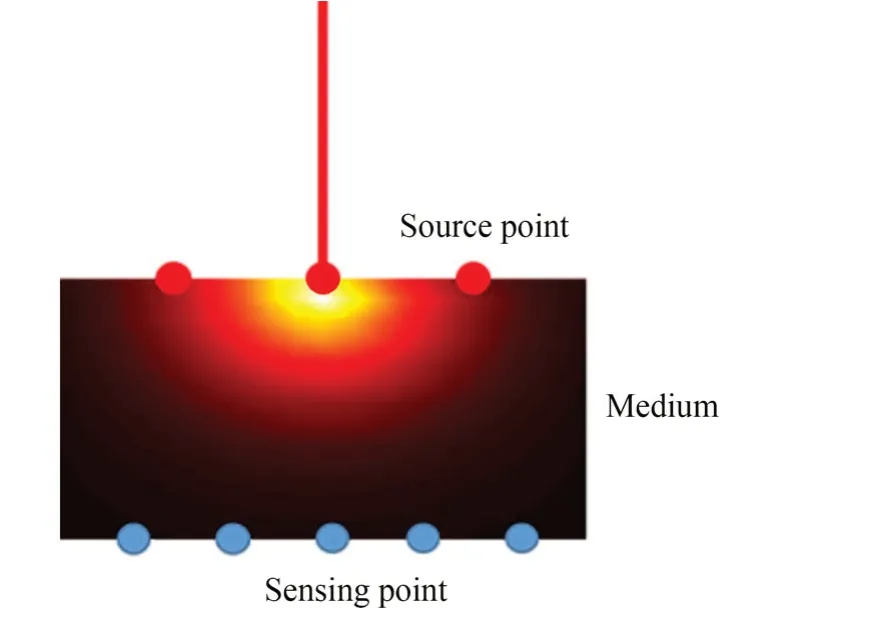
图1 扩散光学层析成像测量过程示意图Fig.1 Measurement process of diffuse optical tomogra⁃phy

DOT 求解算法包含正问题及反问题的求解。正问题求解指的是根据已知的光源探测器分布以及介质参数分布，求解光子传输模型以获取介质表面的能流密度分布。反问题求解指的是通过已知光源探测器分布、介质表面的出射光能流密度分布以及光子传输模型求解介质中的参数分布。由此可见，反问题是一个包含正问题的优化求解问题，求解算法流程如图2 所示。

常见的正问题求解模型有麦克斯韦方程、辐射传输方程和扩散方程等。扩散方程是光源各向同性情况下从辐射传输方程简化而来的，相对辐射传输方程来说具有计算难度低、计算时间快等优点。NIRFAST 软件包［18］是一款被广泛使用的DOT 算法开源软件包，所使用的正问题求解模型即为扩散方程。这里以NIRFAST 软件包使用的正问题求解模型及反问题算法为例介绍图2 中的流程。首先，输入介质的尺寸参数和出射表面测得的能流密度ФM，然后设定初始的吸收散射系数，代入软件包中的扩散方程进行正向问题求解，得到计算的能流密度分布ФC，扩散方程一般为：

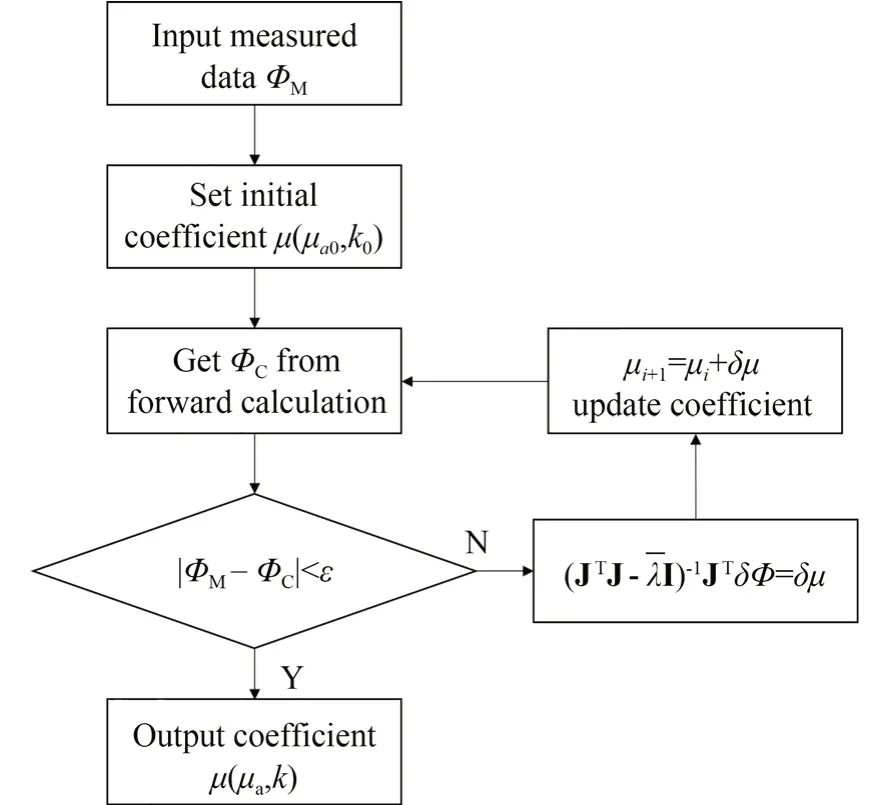
图2 扩散光学层析成像重建算法流程Fig.2 Flow chart of diffuse optical tomography recon⁃struction algorithm

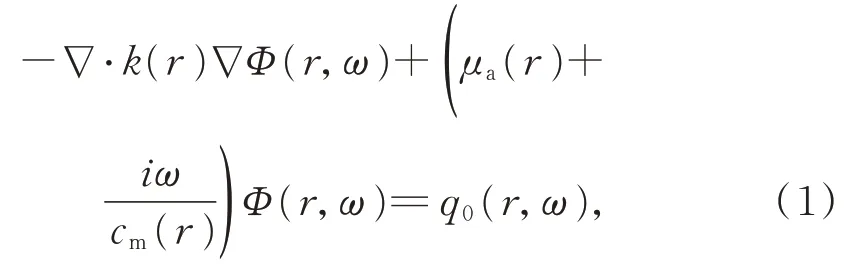
式中：k是约化散射系数，Ф是强度I对角度的积分，也就是能流密度，μa是吸收系数，ω是光的调制频率，对于稳态DOT 来说，调制频率为0，q0是源项。求解该方程一般使用数值方法，包括有限元、蒙特卡洛等。

如果计算所得和测量所得的能流密度分布的差值大于设定的阈值，则根据差值使用式（2）所示的列文伯格-马夸特法确定迭代的参数更新值，进行反向问题求解。

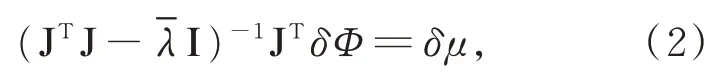
式中：是正则系数，I表示单位矩阵，δФ代表能流密度测量值和计算值之间的差值，δμ代表吸收系数及散射系数的更新值，J 是雅阁比矩阵，是正向计算值对于参数的导数矩阵可以表示为：

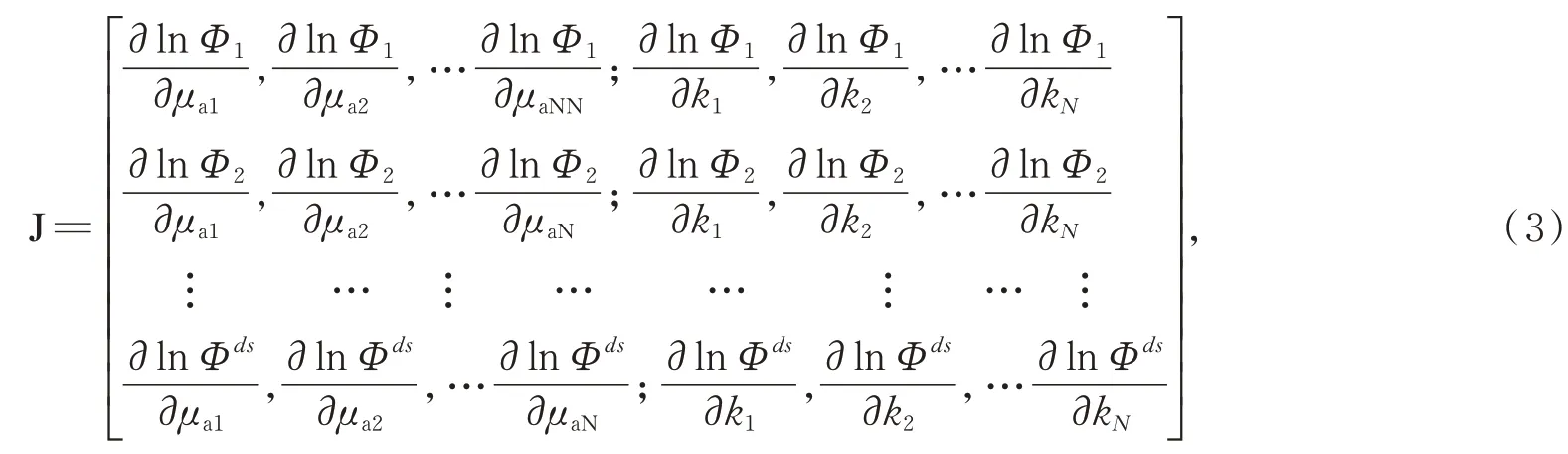
式中：μa和k分别代表吸收系数和约化散射系数，ds为光源位置数量与探测点位置数量的乘积，N表示网格节点数。根据式（2）所得的参数更新值重新进行正向求解，直到能流密度计算值和测量值之间的误差小于阈值。此时的吸收和散射系数分布即为计算重建结果。从式（3）中可以看到，在实际求解过程中，采用了能流密度数值的对数，这要求DOT 系统探测器必须具有较大的动态范围，才能利用软件算法实现高精度的计算重建。

2.2 深度学习网络模型及损失函数

深度学习是机器学习的一种，它使用大量样本进行模型训练，建立起输入样本集和目标样本集之间的模型。在本文中参与训练的数据是一维数据，且输入数据和目标数据长度相同。为了实现数据的训练，选择了全连接网络作为深度学习网络模型。理论上全连接网络对于复杂问题的建模能力略好于卷积神经网络［19］，且能够灵活地调整网络中每一层的大小，能够更容易地实现下采样和上采样。使用的网络模型示意图如图3所示。

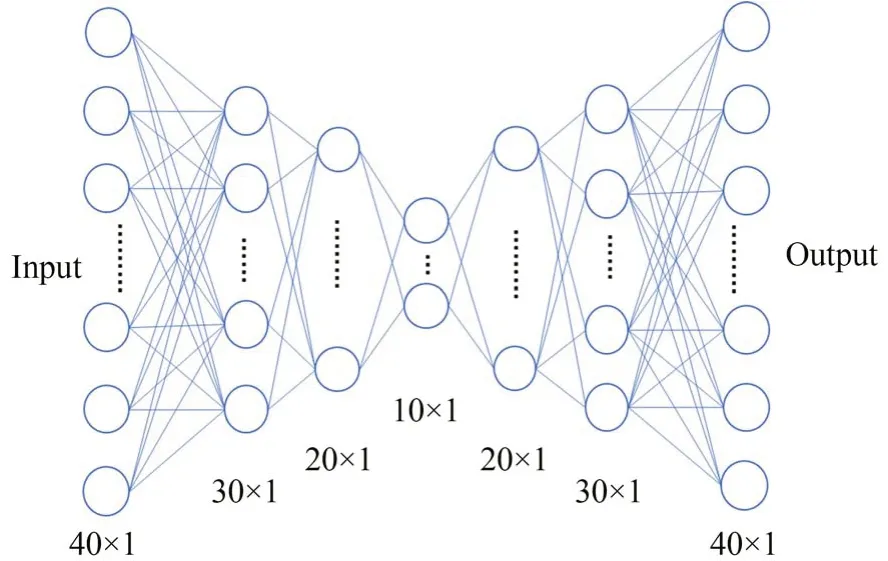
图3 全连接网络示意图Fig.3 Schematic diagram of fully connected network

网络的输入为一个1×40 的向量，经过3 次下采样后变为1×10 的向量，之后再经过3 次上采样变回1×40 的向量。训练的目标是修复由于探测器动态范围受限而测量误差较大的数据，所以在实际训练中，使用NIRFAST 开源程序对不同二维吸收散射特性的介质进行透射能流密度的计算，通过数据截断方法模拟低动态范围探测器的信号获取过程，生成大量训练样本。考虑到这些数据动态范围大的特点，为了使所有数据在训练过程中具有相近的权重，同时为了使训练结果适用于DOT 重建算法，采用式（4）所示的对数处理方法，对由NIRFAST 计算得到的透射能流密度和数据截断后的透射能流密度进行预处理，分别得到网络的目标数据和输入数据，即：

式中：y为网络目标数据和输入数据，Ф为经过NIRFAST 计算出的能流密度及其截断处理后的值。网络的损失函数被设置为有权重的均方差（Mean Square Error，MSE），即有：

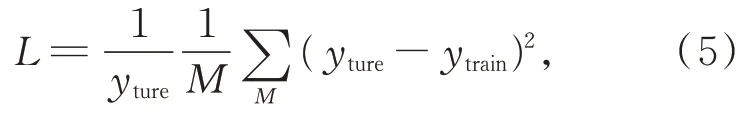
式中：L即为损失值，yture即训练的目标值，M为数据长度，ytrain为经过网络模型输出的数据。该损失函数可以使训练过程中绝对值差异较大的数据具备一致的模型训练收敛性。

3 仿真及实验结果

3.1 深度学习网络模型训练

在模型训练中，吸收散射介质为65 mm×15 mm 的矩形仿体，参考了实际应用中的DOT 系统的光源密度和探测器密度［2-3，6］，把光源位置数设置为4 个，探测点数量设置为10 个，分别等间距地分布于介质上下表面，总探测次数等于光源与探测器位置数量的乘积，即40 次。训练样本中仿体背景的吸收系数分布于0.3~0.5 mm-1之间，异质体的吸收系数分布于0.4~1 mm-1之间。通过设置不同的背景吸收系数、异质体的大小、位置以及吸收系数等参数，计算出的能流密度分布在10-5~10-25内，经过式（4）预处理后，共产生了含有4 000个样本的训练集、100个样本的验证集以及7个样本的测试集。

为了模拟低动态范围探测器（动态范围为103）的信号获取过程，所有能流密度探测数据小于最大值千分之一的数据都会被人为截断，作为一维网络的输入值，利用上述网络模型和损失函数开展训练。在实际训练中，为了展示不同样本量的训练集对于网络预测能力的影响，分别使用了1 000 个样本和4 000 个样本构成训练集进行网络训练，并采用同样的验证集进行检测验证，训练过程中训练集和验证集的损失值下降如图4所示。

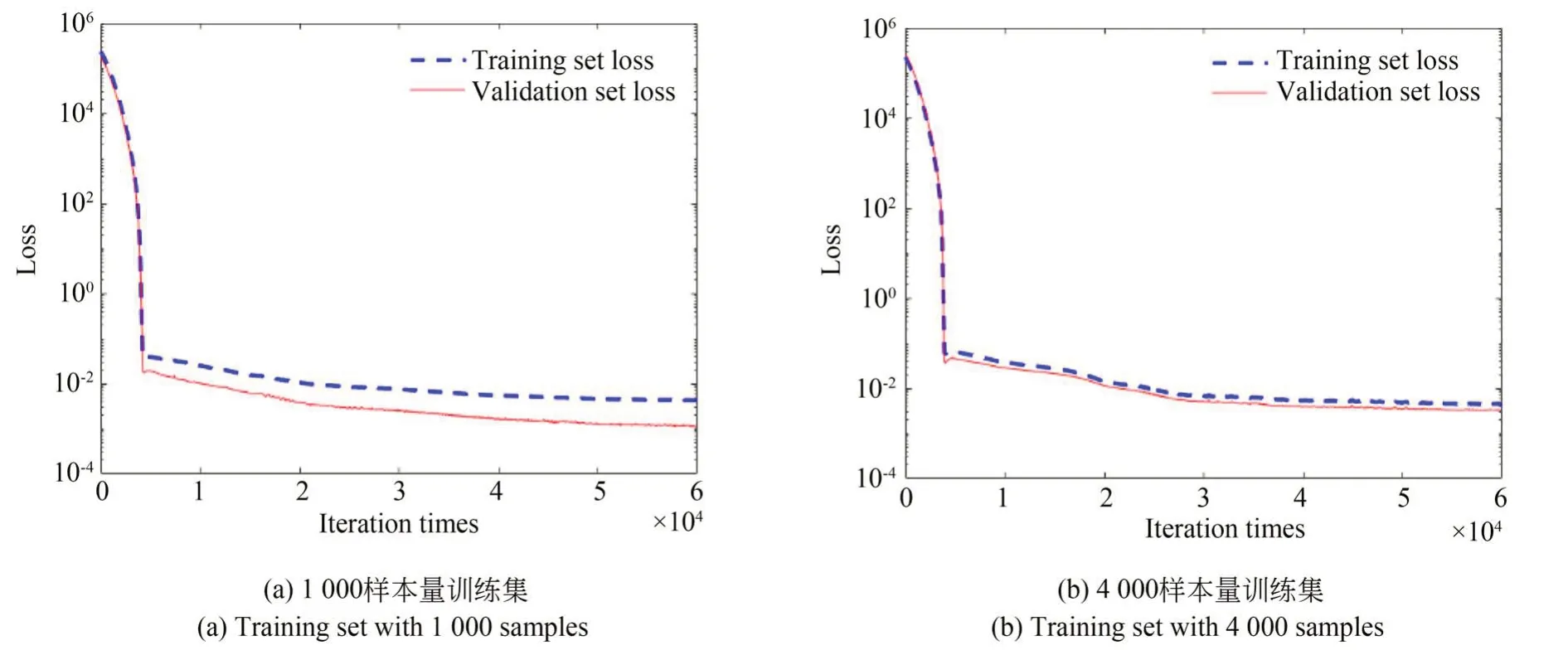
图4 不同样本数量训练集的网络训练误差Fig.4 Errors of training network with different training sets

从图4 中可以发现，网络训练过程中，不论是1 000 样本量还是4 000 样本量，训练集和验证集的误差均呈现下降趋势，这反映了模型训练的有效性。

3.2 仿真验证结果

为对模型性能进行验证和分析，在网络模型训练完成后，把没有参与训练的7 个测试样本输入到网络中，可获得如图5 所示的其中3 个样本的测试结果。图5 展示了按照式（4）预处理前样本能流密度的完整数据、截断数据和修复数据。从图中可以看到，网络模型修复后的数据与截断前的完整数据非常接近，这说明训练好的网络修复了被截断的数据。为了进一步验证网络模型对低动态范围探测器测量数据的修复效果，使用图2 所示流程进行了DOT 重建，重建效果如图6和图7 所示。

图5 不同样本截断数据的修复结果Fig.5 Recovery results of truncated data of different samples

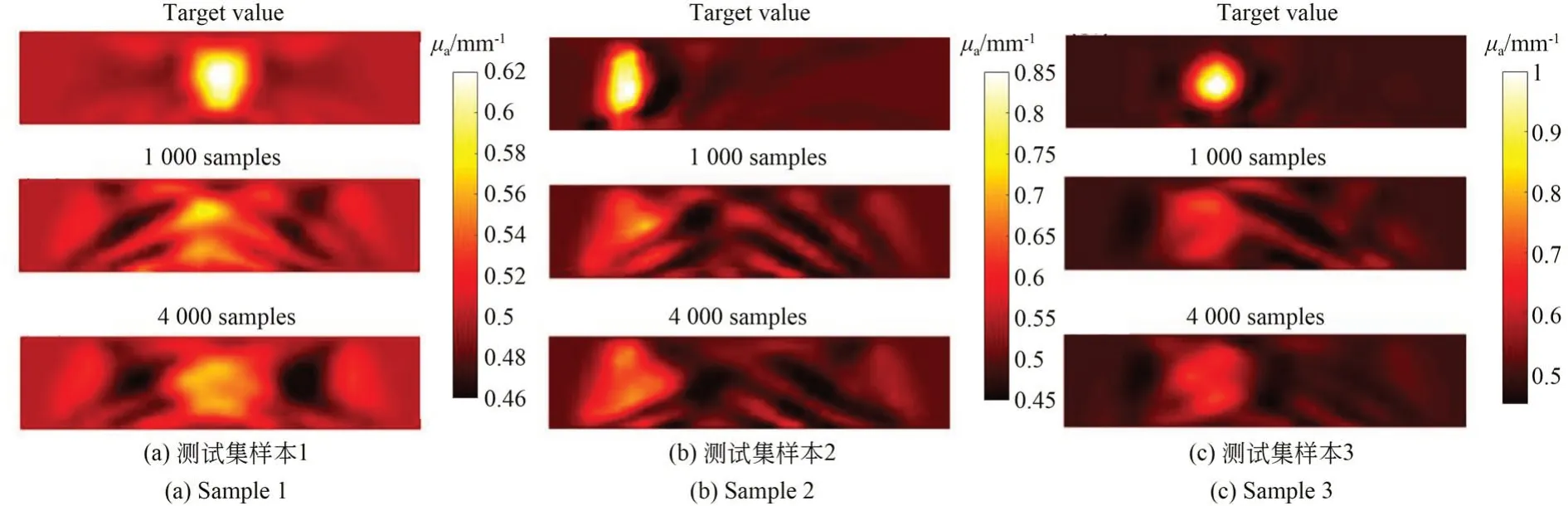
图7 对不同样本修复后数据重建的吸收系数分布效果比较Fig.7 Comparison of reconstructed absorption coefficient distributions of different samples

图6 为利用图5 中所示的被截断处理的数据重建得到的吸收系数分布结果。可以发现，不论仿体和异质体的参数如何设置，模拟低动态范围探测器采集的数据重建结果具有相同的特点，即吸收系数分布中会出现一些高吸收系数（10 mm-1左右）的异常区域，这些高吸收区域的分布呈现空间对称性。该结果说明使用低动态范围探测器采集吸收散射光信号所产生的数据误差严重影响了DOT 的重建效果，对DOT 计算重建来说是不容忽视的。

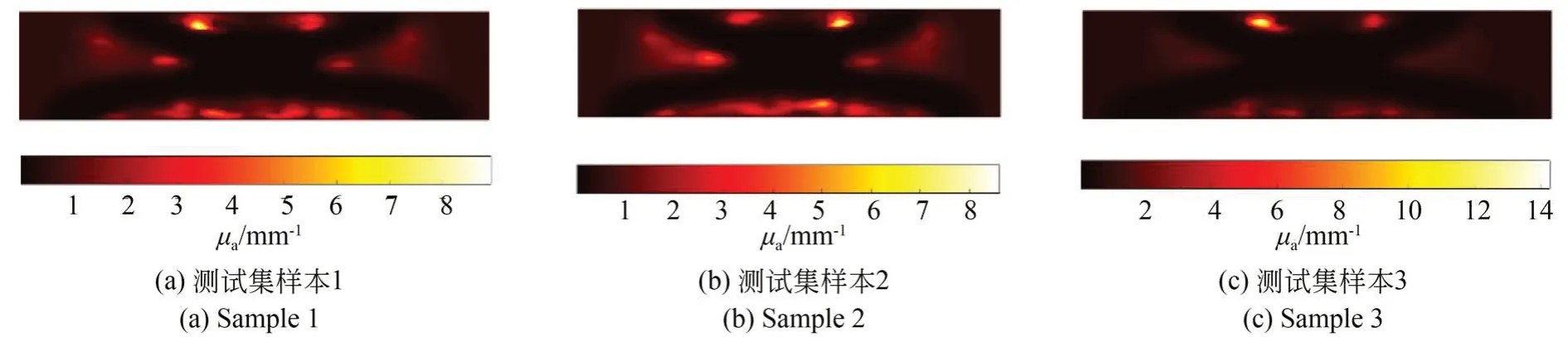
图6 被截断数据的重建吸收系数分布Fig.6 Reconstructed absorption coefficient distribution of truncated data

图7 为分别利用经过图5 中所示完整的数据和网络模型修复后的数据重建得到的吸收系数分布结果。虽然图7（b）和图7（c）中吸收系数重建结果在对比度和空间分布上和图7（a）中的目标值重建结果有偏差，但与图6 中使用截断数据重建得到的吸收系数分布结果相比，使用经过网络模型修复后的预测数据能够成功进行重建。为了进一步分析重建结果，使用均方根误差（Root Mean Square Error，RMSE）和皮尔森相关系数（Pierson Correlation Coefficient，PCC）对图7 中的吸收系数分布进行量化比较，均方根误差越小，皮尔森相关系数越接近于1，这表示由网络模型修复数据重建的吸收系数分布越接近于截断前完整数据的重建结果。数据如表1所示。

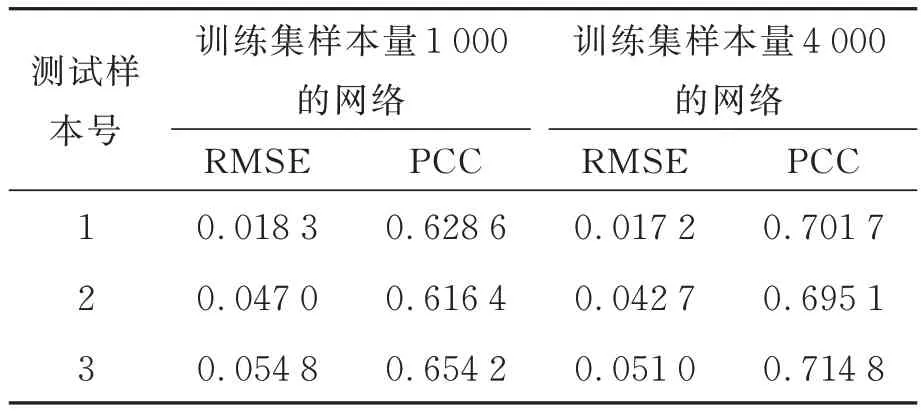
表1 不同训练集样本量训练的网络修复后数据重建的吸收系数分布量化评价结果Tab.1 Quantitative evaluation results of absorption coef⁃ficient of recovery data of network trained by dif⁃ferent training sets

从表1 中可以发现，使用更多训练样本训练出的模型具有更好的数据修复性能，而且修复的数据重建出的吸收系数和截断前完整数据重建出的吸收系数是强相关的。

由此可见，使用深度学习方法对模拟动态范围为103的探测器采集的有误差的DOT 能流密度数据进行修复，能够将探测器的动态范围扩展至1020，经由DOT 重建算法对数据计算后，可以获得较好的吸收系数分布重建结果。模拟结果说明，该方法可以有效扩展探测器的动态范围，减小低动态范围探测器采集信号对DOT 重建结果精度的影响。

3.3 实验结果

在仿真分析的基础上，进一步对利用深度学习方法扩展非接触DOT 系统中探测器的动态范围进行实验验证。首先，参考文献报道［10］搭建了非接触式稳态DOT 系统，系统示意图和实物图分别如图8（a）和图8（b）所示。整个实验系统由三部分组成，分别是在一维方向移动的光源，具有一定吸收散射系数的仿体，以及对仿体后表面进行成像的探测器。

光源部分由光纤输出的激光器（B&W TEK INC. BRM-785-0.55-100-0.22-SMA）、准直透镜（Ocean Insight 74-VIS）、夹持器和电动平移台（Thorlabs LTS300/M）组成。探测器部分由镜头和CCD（DAHENG MV-EM510M/C）组成，其中CCD 的灰阶为8 位，动态范围为256。实验中仿体是采用环氧树脂作为基质，掺杂印度墨水和氧化锌粉末，并加入固化剂进行固化得到的长方体固体，仿体上钻孔填充一定浓度的印度墨水溶液作为异质体，其横截面结构尺寸及吸收系数分布如图8（c）所示。仿体溶液配置过程中，使用吸收光谱法可以确定掺杂印度墨水后的环氧树脂溶液吸收系数，通过调整印度墨水的掺杂浓度，确定溶液吸收系数为0.1 mm-1。根据氧化锌粉末的参数以及Mie 散射理论［20］可计算获得溶液散射系数的理论值，通过调整氧化锌粉末的掺杂浓度，近似确定溶液散射系数为1 mm-1。异质体溶液配置过程中，采用与仿体相同的方法确定其吸收系数为0.3 mm-1。

图8 实验光路及仿体参数分布Fig.8 Experimental optical path and distribution of phan⁃tom parameter

在实验测量过程中，光源及探测器的数量和分布情况同模拟仿真中一致。激光束依次从仿体前表面预设的位置入射，经仿体吸收散射后从后表面出射并被CCD 相机探测。为获得仿体后表面出射光的能流密度分布，通过实验标定法建立了仿体后表面能流密度和CCD 像素灰度值的关系［21］。按照实验中仿体设定的吸收系数及散射系数进行计算，可知能流密度的理论动态范围大约为1010，这远大于实验中CCD 的动态范围。根据3.2 节中仿真模拟得到的结论，在这种情况下想要获得无重建误差的结果，需要对采集到的数据进行修复。

利用3.1 中训练得到的网络模型，对实验采集到的能流密度数据进行修复，结果如图9 所示。从图9 可以发现，实际测量值的动态范围大约为200，修复后数据的动态范围被扩展到109左右。这说明深度学习方法修复了低动态范围探测器采集的能流密度数据，并扩展了探测器的动态范围。使用图9 中的数据进行了吸收系数重建，得到的吸收系数分布如图10 所示。

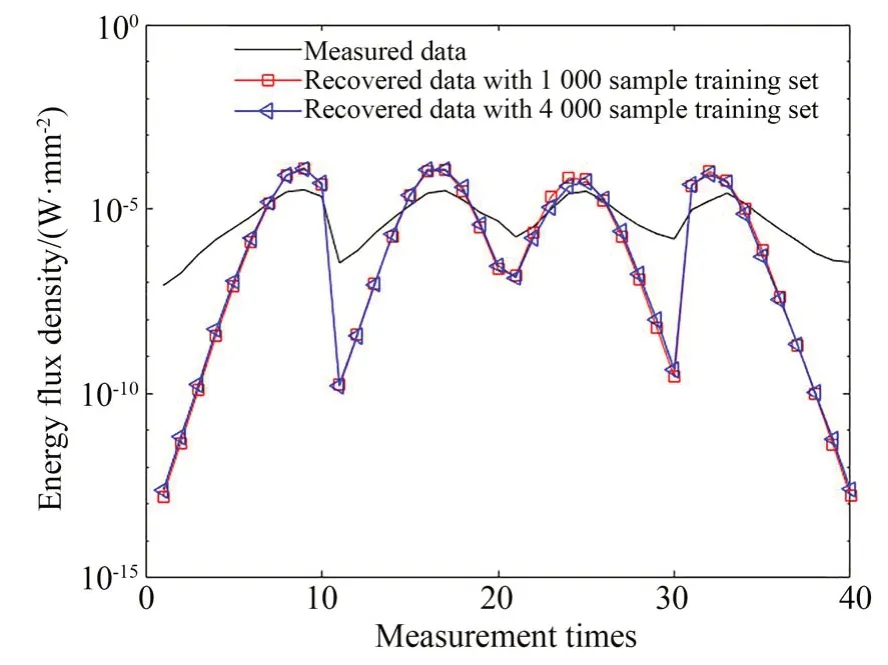
图9 实验采集值及经过网络修复后的值Fig.9 Measured data and data after network recovery

从图10（c）可以发现，使用实验中探测得到的能流密度进行DOT 重建得到的吸收系数分布结果与图8（c）中的预设参数相比有较大的误差，而且吸收系数的空间分布与图6 中仿真截断后数据的重建结果相似。这从实验上验证了探测器动态范围过小会导致探测到的能流密度的误差较大，从而严重影响DOT 的重建精度。图10（a）和图10（b）中的结果则说明了尽管使用不同样本量的训练集训练的网络模型对于数据的修复能力有差异，但是都可以显著提升DOT 重建吸收系数分布结果的精度。在此基础上计算了图10（a）和图 10（b）中的结果与图 8（c）中设定值的RMSE，分别为0.545 和0.542。虽然重建的吸收系数分布和图8（c）的理论预设值之间存在一定的误差，但考虑到实验中运动精度、器件噪声、仿体固化等不确定性因素的影响，该误差是在可接受范围内的。

图10 实验数据及其网络修复后的值的DOT 重建结果对比Fig.10 Comparison of DOT reconstruction results of ex⁃perimental data and its predicted values

实验结果表明，深度学习方法对实验中动态范围为256 的探测器采集的有误差的DOT 能流密度数据进行修复后，能够将探测器的动态范围扩展至109，经由DOT 重建算法对数据计算后，吸收系数分布的重建结果准确。这从实验上证明深度学习方法可以有效扩展探测器的动态范围，减小低动态范围探测器采集信号对DOT 重建结果精度的影响。

4 结 论

本文提出了一种利用深度学习扩展非接触扩散光学层析成像系统中探测器动态范围的方法。首先，使用NIRFAST 软件包生成了一系列模拟低动态范围采集的DOT 数据。其次，使用这些数据完成了一维全连接网络模型的训练。之后分别通过模拟仿真和实验对该模型扩展非接触DOT 系统中探测器动态范围的能力进行了验证。在模拟中，该方法修复了模拟动态范围为103的探测器采集到的含有误差的测试集数据，显著减小了数据误差对DOT 重建结果精度的影响，理论上将探测器的动态范围扩展到1020；在实验中，制备了实验仿体并搭建了一套非接触DOT 系统，使用动态范围为256 的CCD 相机完成了DOT 系统的实验数据采集。利用本文提出的方法对采集到的数据修复后，可重建得到与预设仿体吸收系数分布基本一致的重建结果，将DOT 系统中探测器的动态范围从256 扩展到109。虽然模拟和实验中通过网络模型修复的数据重建出的吸收系数结果的精度还有待提高，但该方法能够有效修复低动态范围探测器所采集的有误差的DOT 数据，减小它对DOT 重建结果精度的影响，为利用非接触DOT 系统探测高吸收散射介质或大面积探测提供了一个可行的解决方案，使得非接触式DOT 系统有了更广阔的应用空间。

目前，该方法只对单层的仿体进行了验证。如果进一步修改DOT 求解模型，使之能适用于多层不同介质组成的仿体，该方法还可以应用到更复杂的多层仿体或生物组织上。