基于可信性的二维二元语义多属性群决策方法

伊长生, 牛家强, 潘瑞林

(安徽工业大学管理科学与工程学院,安徽马鞍山 243032)

1 引 言

随着社会经济的快速发展和事物本身的复杂性加剧,多属性决策问题在社会、经济、文化以及企业的生产运营管理等领域得到了广泛应用,如复杂产品协同开发的供应商选择问题[1],医疗服务机构的满意度测评[2],设备开发方案的选择问题[3]等.而多属性决策过程,实质上就是决策者在一组具有一定属性的备选方案中选出最优方案的过程,这些属性可能是定量的也可能是定性的.然而在现实的多属性决策过程中,考虑到信息本身的自然属性以及人类思维的主观性和模糊性,决策者往往不能精确地以量化的形式给出评价信息,只能粗略地以定性的语言短语的形式给出评价信息.为此,Zaheh[4]最先提出了用语义变量(如“差”、“一般”、“好”等)来给出评价信息,使得表达更加符合决策者的意识.基于此种方法,已有学者提出了一些相关的语言运算模型[5,6],但这些模型存在着运算结果常常与事先定义的语言评价集中的元素不一致的问题,只能近似地用语言评价集来代替.为了解决此类信息缺失和运算结果不精确的问题,Herrera 等[7]提出了二元语义分析模型,并在实际决策问题中得到了广泛应用.近年来,学者们针对二元语义模型展开了多种形式的扩展研究.比如,Wang 等[8]基于“符号比例”的概念提出了比例二元语义模型;张永政等[9]提出了基于二元语义和D 数的语义评价信息表达;黄必佳等[10]通过综合应用语义标度提出了基于TOPSIS 和二元语义的LTOPSIS-2T 模型;黄海燕等[11]基于区间复合标度考虑了个人喜好差异,提出一种新的二元语义模型.

然而,单纯的二元语义模型仅考虑到决策者对决策对象本身的评价,而忽略了评价结果的可靠性程度,这在某种程度上会影响初始决策信息的准确性.因此,朱卫东等[12]提出了二维语言信息,在传统二元语义模型的基础上增加了一维表示专家判断可靠性程度的第二维语言信息,使得利用该模型表达语言评价信息时更加可靠准确.正是由于二维语言信息在语言表达上更加准确,关于二维语言多属性决策方法的研究逐步成为学术界研究的焦点问题.具体研究可以分为两类: 其一是针对二维语言信息表达的量化研究.张晨等[13]通过证据推理原理给出了二维语言识别框架,进而定义了基于证据推理的二维语言信息.Zhu 等[14]提出了一种用于二维语言运算和表达的格蕴涵代数,以此达到使二维语言信息更易于理解的目的.其二是针对二维语言算子的研究.二维语言有序加权算子[15]以及依赖型集结算子[16]被相继提出并应用于二维语言多属性决策问题.Liu 等[17]在二维不确定性语言信息[18]的基础上进行了深一步研究,定义了二维不确定性语言Power 算子.Liu[19]提出了基于扩展TOPSIS 的二维不确定性语言群决策方法.

基于上述分析,为了充分发挥二元语义模型的灵活性、精确性以及二维语言信息在初始决策意图表达上的准确性,尤其是多属性群决策中对两个维度信息的处理问题,有必要进一步拓展关于二维二元语义群决策方法的研究.目前,关于二维二元语义群决策方法的研究少之又少,研究成果甚是匮乏,而且现有的相关文献也存在一定程度的不足之处.比如,吴良刚等[20]提出改进的二元语义模型,定义了二维二元语义及其加权平均算子,但所采用的语言评估标度并不合理,而且二维二元语义期望值函数,其实质只是将一、二维语言信息简单的相乘,并没有考虑到第二维语言本身所存在的意义.王泽林[21]提出了一种新的关于二维二元语义的比较方法和距离公式,进而给出了权重信息完全未知的二维二元语义多属性群决策方法,其中的信息重要程度比例系数并不能通过精确的计算得出,只能人为设定,主观性较大.

针对二维二元语义群决策研究中存在的信息处理不精确问题,本文提出一种基于可信性测度的二维二元语义群决策方法.考虑到非平衡语言标度更加符合决策者的心理判断,提出了一种基于正态分布的二元语义模型.考虑到第二维语言本身所具有的意义,利用可信性测度[22]提出了一种确信度函数,进而构建了新的二维二元语义期望值函数和距离函数.根据决策者和各属性的相应权重求出备选方案的最终期望值,进而对方案进行排序.通过一个可再生能源选择的算例分析验证了该方法的可行性和科学性,并对决策结果进行了敏感性分析,分析结果表明该排序方案具有显著的鲁棒性.

2 二维二元语义表示模型

2.1 二元语义

Herrera 等[7]提出的二元语义模型能有效避免信息失真和提高计算准确性.下面给出二元语义的定义.

定义1[7]设S={s0,s1,...,sg}是一个语言评价集,S中的语言评价值经过某种集结方法得到的实数为θ ∈[0,g],则θ对应的二元语义信息可由如下的函数Δ表示,即

其中round 表示“四舍五入”算子,si表示语言评价集S中的第i个元素,αi=θ −i,称为符号转移值.

该定义可以由图1 作进一步说明[23],其中语义变量S介于s5和s6之间,则可用二元语义表述为(s5,α).

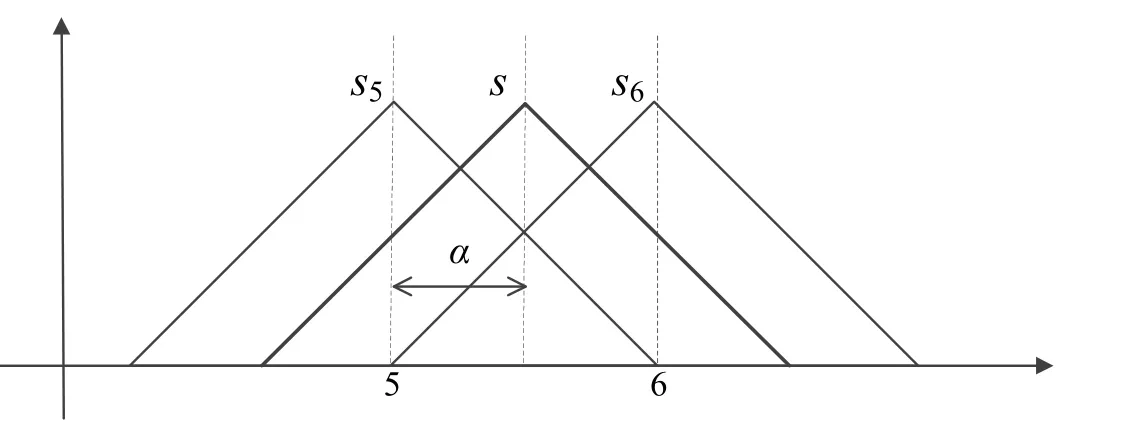
图1 二元语义变量Fig.1 Variable of 2-tuple linguistic information

定义2[7]若存在一个二元语义(si,αi),则与其相对应的实数值θ可由一个逆算子Δ−1转换而得,即

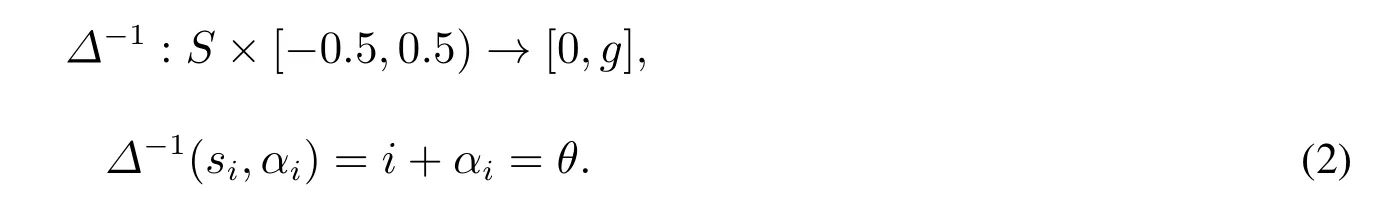
2.2 二维二元语义

二维二元语义包括两种常见的语言评价集, 其中第一个维度, 如S={s0= 特差,s1= 很差,s2=差,s3= 较差,s4= 中等,s5= 较好,s6= 好,s7= 很好,s8= 特好},是用于表征决策者给出的关于备选方案本身的评价结果; 第二个维度, 如C={c0= 很没把握,c1= 没把握,c2= 一般,c3= 有把握,c4=很有把握},是用于表征决策者对给出评价结果的可靠性的自我评价[12].二维二元语义较之一维二元语义能够对具有不确定语言信息的备选方案进行更为精确的评估.下面给出二维二元语义的定义.

定义3[21]假设存在两个语言评价集S={s0,s1,...,sg}和C={c0,c1,...,ck},则=〈(sit,αit),(cjt,αjt)〉为一组二维语言变量,其中sit ∈S,cjt ∈C,αit,αjt ∈[−0.5,0.5).

定义4[21]设=〈(sit,αit),(cjt,αjt)〉,t= 1,2,...,n为一组二维二元语义变量,与其相对应的权重向量为W=(w1,w2,...,wn)T,wt ∈[0,1]且=1,则二维语言加权平均算子为

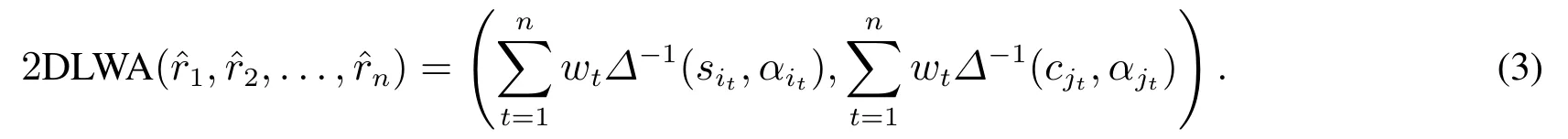
2.3 可信性测度

可能性测度、必要性测度和可信性测度为模糊数学中三种相对重要的测度[22],而可能性测度以往总被人们看作是与概率测度对等的概念.实际上,可信性测度才是在模糊数学中充当着概率测度的角色.可信性测度的定义以及相关性质如下.

定义5[24]假定Θ为一非空集合,P(Θ)是集合Θ的幂集,则对于P(Θ)中的任一模糊事件A都有一实数值Cr{A}表示其可信性测度,同时Cr{A}必须满足以下4 条性质.

性质1Cr{Θ}=1.

性质2当A ⊂B时,Cr{A}≤Cr{B}.

性质3Cr 具有自对偶性,即对任意A ∈P(Θ),总有Cr{A}+Cr{Ac}=1,其中Ac为A的对立事件.

性质4对于任意Cr{Ai}≤0.5 的事件Ai,都有Cr{∪i Ai}=sup为上界.

定义6[24]假设Θ为一非空集合,它的幂集为P(Θ),Cr 表示可信性测度,则三元组(Θ,P(Θ),Cr)称为可信性空间.

定理1[24]设ξ是可信性空间(Θ,P(Θ),Cr)上的一个模糊变量,t为任一实数,则模糊变量ξ的隶属度函数可以通过以下的可信性测度公式导出

据此,有可信性测度的反演定理.

定理2[24]若模糊变量ξ的隶属函数为µ,则对于任何一个实数集A均有

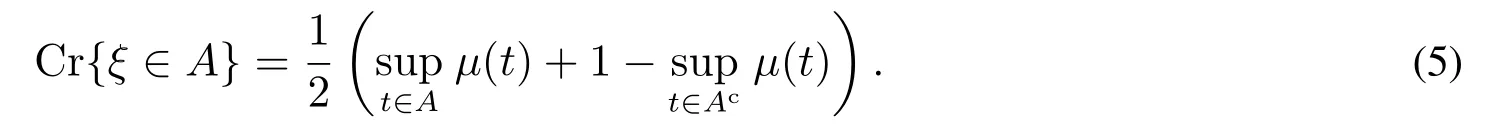
2.4 基于正态分布的二元语义模型

本文给出基于正态分布的二元语义表示模型,在此基础上提出新的二维二元语义距离函数和期望值函数,并据此构建基于可信性测度的二维二元语义表示模型.

2.4.1 基于正态分布的语言评估新标度

Pei 等[25]提出了四类基于正态分布的不均匀尺度集.考虑到合理的语言尺度集应包括好与坏两个方向,并且是关于中间值对称分布的;此外,随着标度值的下标绝对值的增加,标度值应变得越来越稀疏.所以,本文选取第一类语言尺度集作为语言评估标度.基于正态分布N(0,σ2)的语言尺度集的相关定义如下.

定义7[25]假设语言尺度集S={s−i,s−(i−1),...,s0,...,si−1,si},i= 1,2,...,n,则正语言尺度值可以由下式得到,即

其中Φ−1代表累计概率分布函数Φ的逆函数.同理,根据正态分布的对称性原则,当i<0 时也可根据式(6)求出相应的语言尺度值.

例1取σ= 1,i= 4 时, 有S={s−4= 极差,s−1.15= 很差,s−0.675= 差,s−0.32= 较差,s0=一般,s0.32=较好,s0.675=好,s1.15=很好,s4=极好}.

在该语言标度中,相邻语言标签下标之间偏差的绝对值随着语言标签值的增大而增大.德国心理学家费希纳也曾提出了著名的韦伯–费希纳定理[26],即Ψ=κlgϵ,其中Ψ为人的主观感觉量,ϵ为客观刺激强度,κ为韦伯常数.当刺激大小在以几何级数上升时,感觉的量值在以算术级数上升.由此可见,该语言标度是合理的,并且符合专家的心理判断和对客观刺激的主观感受.

2.4.2 基于新标度的二元语义模型

基于文献[25]的语言评估尺度集,提出语义度量函数φ(si),φ(si)→δ(i)∈[−4,4],其中

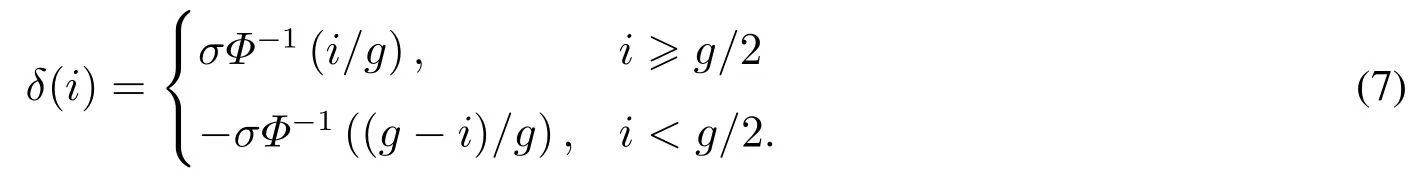
下面给出改进后的二元语义模型及其相关的定义.

定义8设S={s0,s1,...,sg}为一组语言评价集,其中si ∈S,i= 0,1,...,g,实数θ ∈[−4,4]为S中的语言评价值通过某种集结方法得到的结果,则与实数θ相对应的二元语义值可以通过函数Δ获得,

即Δ:[−4,4]→S×[−0.5,0.5),

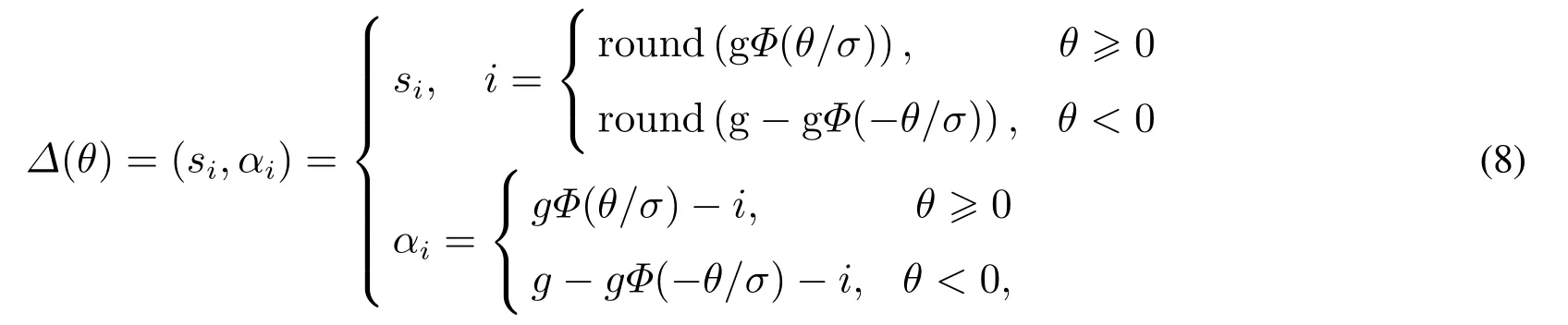
其中αi ∈[−0.5,0.5),语言评价集S中元素个数为(g+1).

定义9若存在一个二元语义(si,αi), 其中i= 0,1,...,g,αi ∈[−0.5,0.5), 则与其相对应的实数值θ ∈[−4,4]可以通过函数Δ−1得到,即Δ−1:S×[−0.5,0.5)→[−4,4],

2.5 基于可信性测度的二维二元语义模型

当决策者在决策过程中运用二维二元语义变量作为评价信息时,第二维语言评价值是为了表征决策者对自己给出的评价结果的可靠程度大小,即该评价结果的可信性大小.而在决策者自身知识、经验水平有所保障并且完全理性的情况下,没有人比决策者更了解自己评价结果的可信性程度,因此,在决策过程中第二维语言评价信息的价值应给予重视.事实上,第二维语言评价值体现了决策者对于第一维语言评价值的不确定性,而这种不确定性如果只用单一的语言评价值来表征,显然不够科学也不符合常理,如仅仅只采用“熟悉”、“一般”、“不熟悉”等单一语言评价值来表示对所给出评价结果的可信性程度,明显存在着决策者“不怎么熟悉也不陌生”的情况.因此,本文基于可信性测度提出一种新的方法来解决上述问题.

令zj表示第一维语言评价值si对评价等级cj的隶属度,rj= Cr{cj=zj}表示某个模糊事件{cj=zj}发生的可信性测度大小,即表示待评估对象在第一维语言评价集si下的隶属值zj归于评语等级cj的可信性测度,其中i=1,2,...,g,j=0,1,...,k.根据可信性反演定理可得

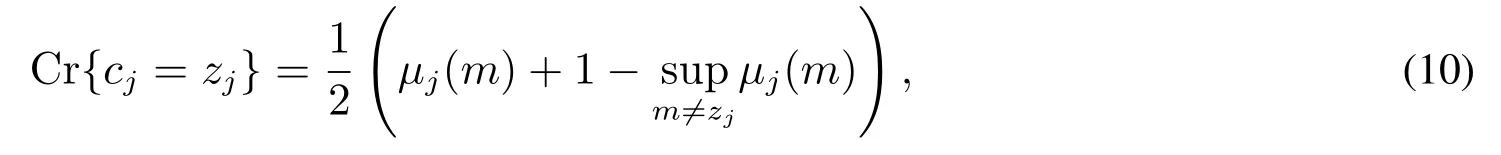
其中µj(m)代表在第一维语言评价值si下m归于各个语言评价等级cj的隶属度大小.隶属值zj可用决策者在各个评语等级cj下自我打分的百分比表示.

设ν为确信度函数,表示对决策者所给出评价结果的可信性程度,ν可由如下公式给出,即

其中cj ∈C,j=0,1,...,k.

例2设第一维语言评价集为S={s0= 特差,s1= 很差,s2= 差,s3= 较差,s4= 中等,s5=较好,s6= 好, s7= 很好,s8= 特好}, 第二维语言评价集为C={c0= 很没把握,c1= 没把握,c2=一般,c3= 有把握,c4= 很有把握}.专家E从X1,X2,...,X5五个属性下分别对备选方案A进行评估的第一维语言评价值为(s6,s5,s4,s5,s5),专家E给出的关于备选方案A评价值的隶属度如表1 所示.

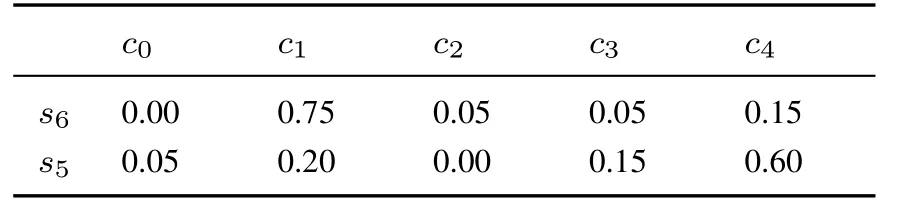
表1 专家E 给出的关于方案A 评价值的隶属度Table 1 The membership degree of evaluation value of A by E

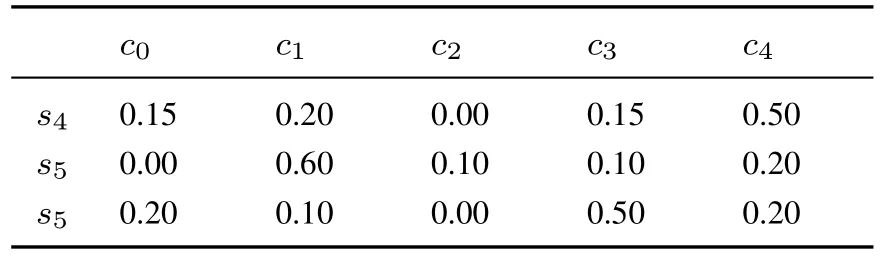
续表1Table 1 Continues

由式(10)计算可得相应的可信性测度为

由式(11)计算可得确信度为ν=(2.350,4.325,4.425,3.150,4.150).

通过例2 可知,在评价信息需采用二维语言表示时,确信度函数可以对第二维语言信息进行准确的量化处理,将决策者对所给出评价结果的把握程度转化为能够计算的确信度.将其代入合适的期望值函数中,从而准确地计算出能够反映决策者真实决策意图的期望值.

推论1若隶属度z0=z1=···=zj,j=0,1,...,k,则确信度函数ν退化为语言评价集C的均值.

证明因为隶属度zj为决策者在各个评语等级cj下自我打分的百分比,故zj明显满足以下约束条件

若有z0=z1=···=zj,j=0,1,...,k,根据式(12)可知,必有z0=z1=···=故此时的确信度函数退化为即此时的确信度函数表示语言评价集C的均值. 证毕.

推论2设cj,j=0,1,...,k表示第二维语言评价值,zj表示第一维语言评价值对cj的隶属度大小,则

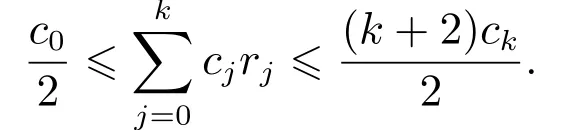
证明由式(10)和式(11)可得

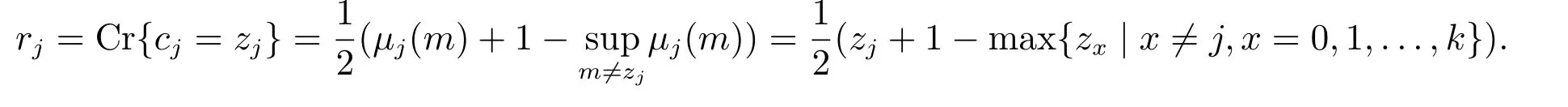
从而有

再由式(12)可知0 ≤zj≤1 且=1,故

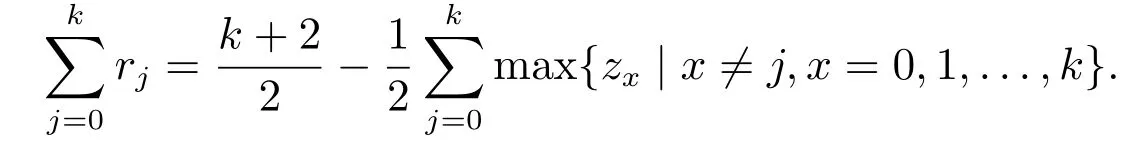
易知max{zx |x=j,x=0,1,...,k} ∈[0,1], 故可得取min{cj}=c0, 可得再取max{cj}=ck,可得. 证毕.

设语言评价集S={s0,s1,...,sg}表示第一维语言信息评价值的集合,C={c0,c1,...,ck}表示第二维语言信息评价值的集合,实数θ ∈[−4,4]为S中语言评价值通过某种方法集结得到的结果,则相应的二维二元语义信息=〈(si,αi),ν〉可通过函数Δ获得,即

其中i=

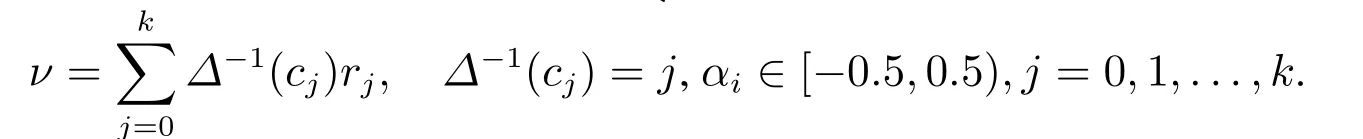
相反,若存在一个二维二元语义〈(si,αi),ν〉,则与其相对应的实数值θ ∈[−4,4]可由函数Δ−1获得,即

其中θ=

可以证明上述二维二元语义的期望值函数满足如下性质.

性质1若(sit,αit)相同时,νt越大则相应的二维二元语义越大.

证明当(sit,αit)相同时,由式(15)可知,期望值E[ˆrt]是关于νt的增函数,故νt越大,则期望值E[ˆrt]越大,所以相应的二维二元语义越大. 证毕.

性质2若νt相同时,(sit,αit)越大,则相应的二维二元语义越大.

证明当νt相同时,由式(15)可知,期望值函数E[ˆrt]是关于Δ−1(sit,αit)的增函数.若(sit,αit)越大,那么Δ−1(sit,αit)就越大,故期望值E[ˆrt]就越大,所以相应的二维二元语义就越大. 证毕.

性质3当νt=1 时,该二维二元语义降为普通的一维二元语义.

证明当νt= 1 时,由式(15)可知,期望值E[ˆrt] =Δ−1(sit,αit),不难发现此时的二维二元语义的比较就是传统二元语义的比较,即该二维二元语义退化为一维二元语义. 证毕.

性质4当νt=0时,该二维二元语义信息无效.

证明当νt=0 时,由式(15)可知,期望值E[ˆrt]为0,即该二维二元语义无效,故性质4 得证. 证毕.

设Vt=〈(sit,αit),νt〉,t= 1,2,...,n为一组二维二元语义, 与其相对应的权重向量为W=(w1,w2,...,wn)T,wt ∈[0,1]且=1,则二维语言加权平均算子为

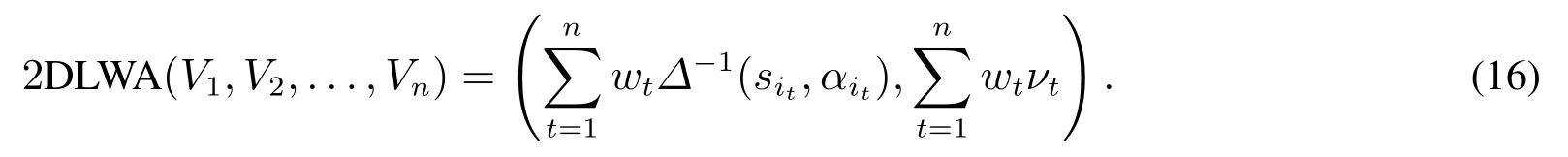
设二维二元语义V1=〈(si1,αi1),ν1〉和V2=〈(si2,αi2),ν2〉,则它们之间的距离为

3 二维二元语义多属性群决策步骤

对于一般的多属性群决策问题, 假设决策者要从方案集A={A1,A2,...,Am}选出最优方案并进行优劣排序.X={X1,X2,...,Xn}表示需要考虑的属性集,W= (w1,w2,...,wn)T为属性权重;E={E1,E2,...,El}表示参与评估的决策者集合,λ= (λ1,λ2,...,λl)T为决策者权重.专家Eh(h=1,2,...,l)针对备选方案Aq(q= 1,2,...,m)的属性Xp(p= 1,2,...,n)给出的一维语言评价值为构成的一维语言评估矩阵为Dh=()m×n.

步骤1计算专家Eh给出的第一维语言评价值对于第二维语言评价等级的确信度函数.

1)专家给出第一维语言评价值归于第二维语言评价等级的隶属度zhqpj.

2)利用式(10)求出模糊事件{cj=发生的可信性测度大小,即

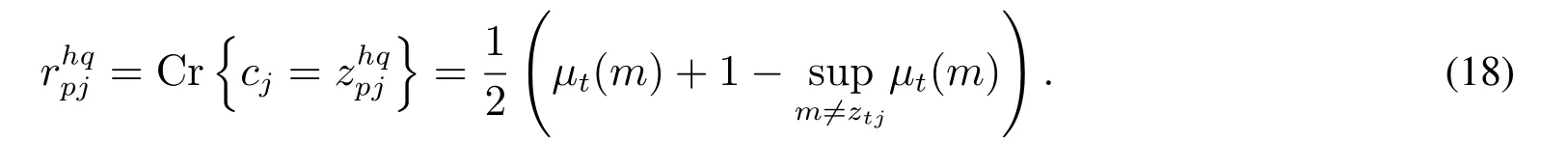
3)根据求出的可信性测度大小,利用式(11)可求得确信度,即

步骤2将专家给出的一维语言评估信息转化为二维二元语义.

1)对专家给出的一维语言评价值进行标准化处理.

对于成本型属性cp,将其评价值标准化为=neg();对于效益型属性cp,将其评价值标准化为=,即

3)构建专家Eh的二维二元语义决策矩阵.

步骤3确定决策者权重.

个体决策者Eh所应占的权重λh可依据个体决策与群体决策之间的差值来计算[27].

λh=为决策者Eh与群体决策之间的差值,h=1,2,...,l.

若该个体决策与群体决策之间的差值越小,则其所应占的权重越大;反之,则其所应占的权重越小.

步骤4 构建综合决策矩阵.

依据决策者的权重对信息进行集结,形成综合评价矩阵D= ()m×n.综合评价值可由二维二元语义加权平均算子求得,即

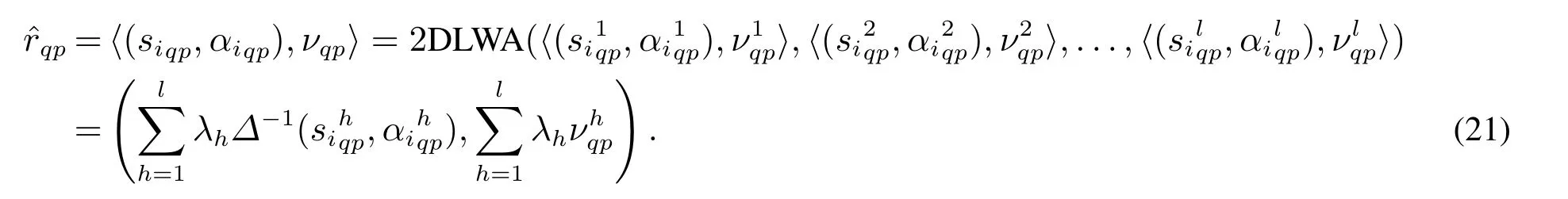
步骤5利用兼顾序信息和强度信息的主客观组合赋权法求出各属性的权重.

考虑到主观赋权法和客观赋权法各有优劣,而一般的组合赋权法中主客观权重系数只能靠人为主观给出,故本文采用文献[28]中的方法来计算属性权重,求解下列组合赋权模型以获得属性的组合权重,即

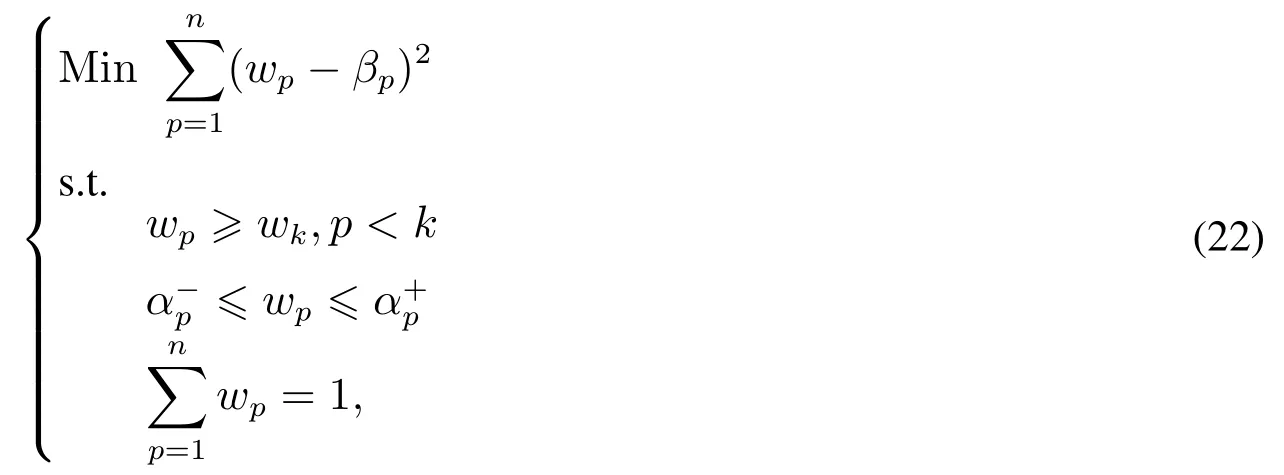
其中wp表示第p个属性的组合权重,βp表示第p个属性的客观权重,表示第p个属性的组合权重下界,α+p表示第p个属性的组合权重上界.

步骤6求出最优方案,确定备选方案的优劣排序.

1)利用二维二元语义加权平均算子计算出每个方案下的二维二元语义最终值,即

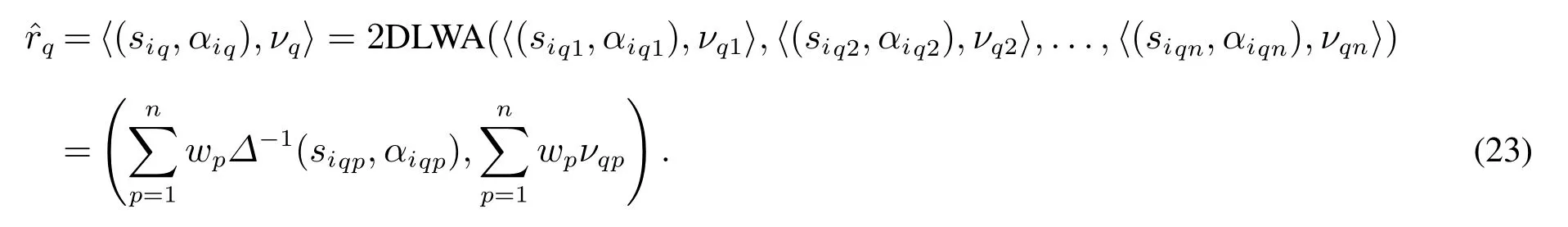
2)根据式(15)可求得各个方案的期望值,即

进而确定优劣顺序,选出最优方案.

4 算例分析

随着化石能源的大规模开采以及工业城镇化进程的加快,能源枯竭以及环境污染问题日渐突出.为了缓解能源匮乏以及应对生态环境污染的难题,可再生能源的开发与利用逐渐成为民众关注的热点问题.为了选择最适合开发利用的可再生能源,有关部门邀请三位专家E1,E2,E3,从经济效益X1,资源丰富度X2,技术水平X3,环境压力X4,社会支持及国家政策X5等方面,对三个方案风能A1,水能A2,太阳能A3进行评估.第一维语言评价集为S={s0= 特差,s1= 很差,s2= 差,s3= 较差,s4= 中等,s5= 较好,s6=好,s7= 很好,s8= 特好}, 第二维语言评价集为C={c0= 很没把握,c1= 没把握,c2= 一般,c3=有把握,c4=很有把握}.三位专家对三种不同的待选方案做出的一维语言评价矩阵如表2～表4 所示.

表2 专家E1给出的一维语言评估矩阵D1Table 2 One dimension assessment matrix D1 given by E1

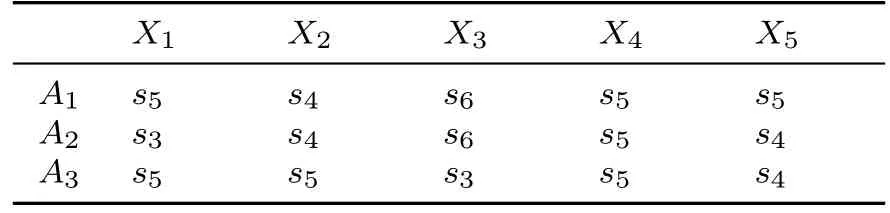
表3 专家E2 给出的一维语言评估矩阵D2Table 3 One dimension assessment matrix D2 given by E2

表4 专家E3 给出的一维语言评估矩阵D3Table 4 One dimension assessment matrix D3 given by E3

4.1 评价决策过程

步骤1专家给出的第一维语言评价值对于第二维语言评价集的隶属度,如下表5～表13所示.

表5 专家E1 给出的关于方案A1 评价值的隶属度Table 5 The membership degree of evaluation value of A1 by E1

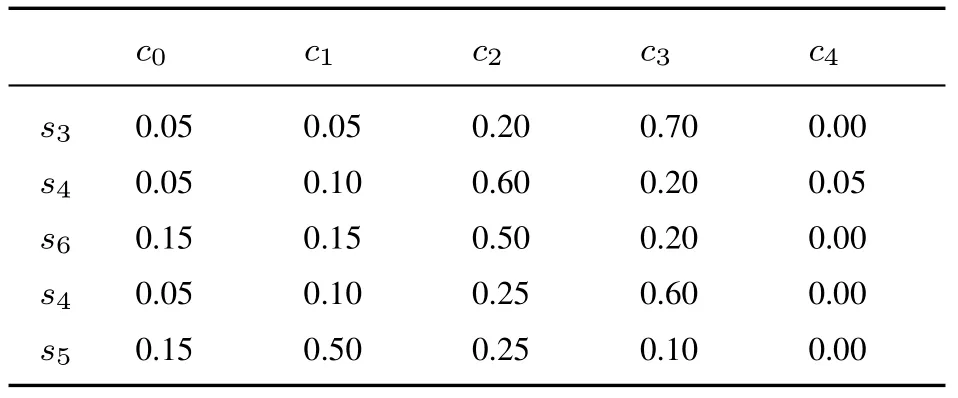
表6 专家E1 给出的关于方案A2 评价值的隶属度Table 6 The membership degree of evaluation of A2 by E1

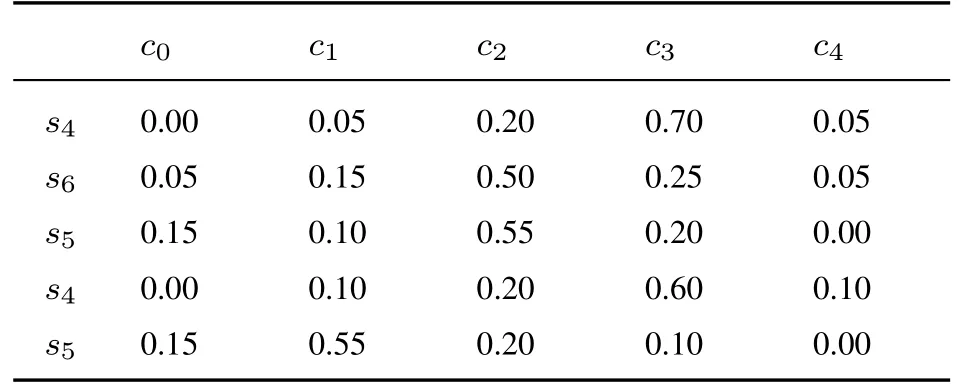
表7 专家E1 给出的关于方案A3 评价值的隶属度Table 7 The membership degree of evaluation value of A3 by E1

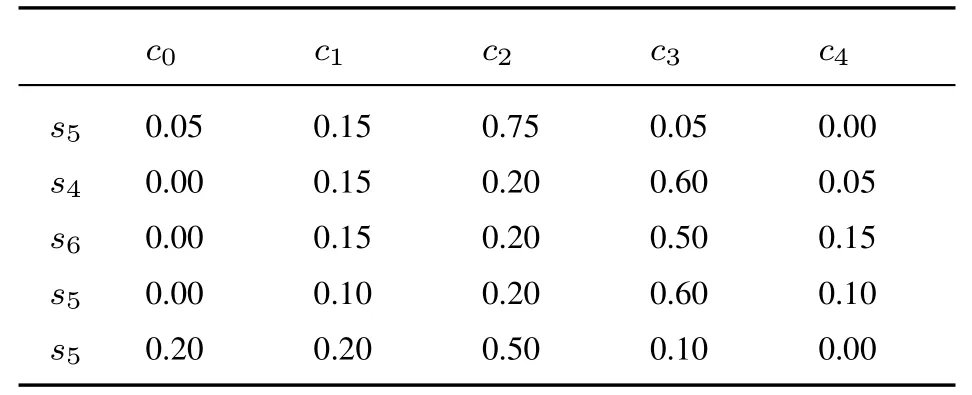
表8 专家E2 给出的关于方案A1 评价值的隶属度Table 8 The membership degree of evaluation value of A1 by E2

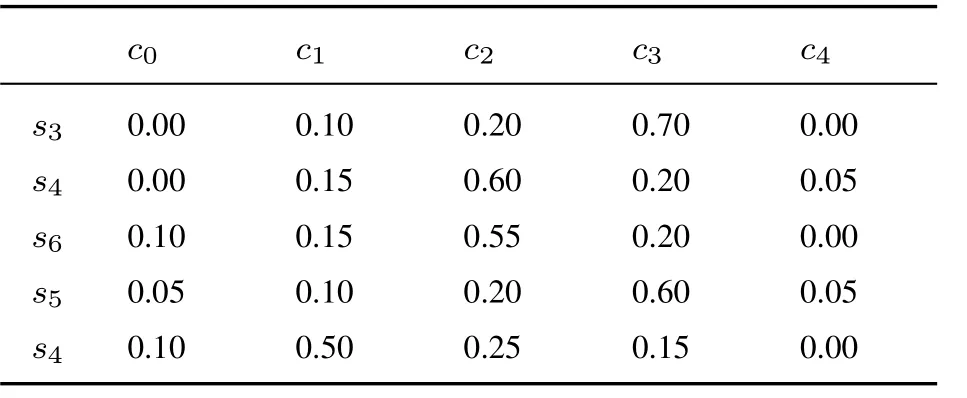
表9 专家E2 给出的关于方案A2 评价值的隶属度Table 9 The membership degree of evaluation value of A2 by E2

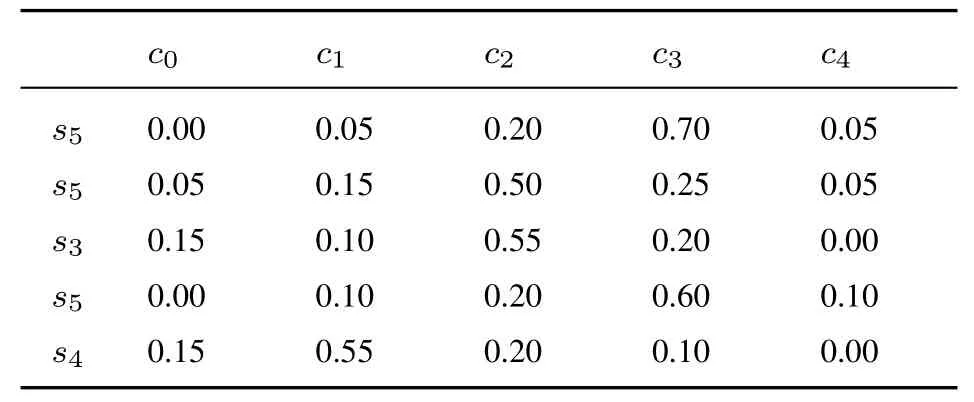
表10 专家E2 给出的关于方案A3 评价值的隶属度Table 10 The membership degree of evaluation value of A3 by E2

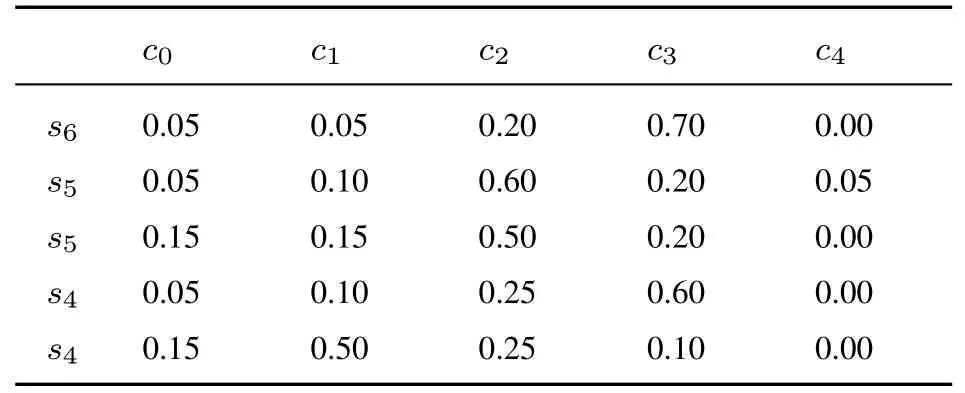
表11 专家E3 给出的关于方案A1 评价值的隶属度Table 11 The membership degree of evaluation value of A1 by E3

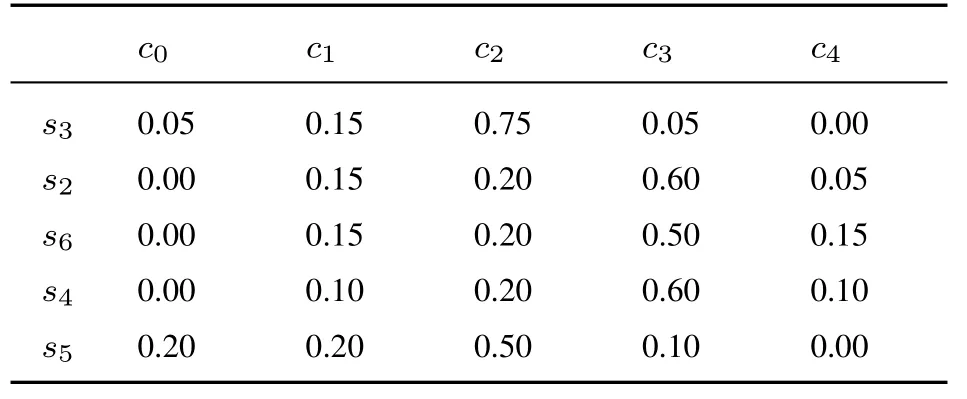
表12 专家E3 给出的关于方案A2 评价值的隶属度Table 12 The membership degree of evaluation value of A2 by E3

表13 专家E3 给出的关于方案A3 评价值的隶属度Table 13 The membership degree of evaluation value of A3 by E3

由式(18)计算可得相应的可信性测度

由式(19)计算可得确信度函数

步骤2通过式(20)将一维语言评价值标准化为,进而根据式(13)将其转化为二维二元语义,可得决策矩阵～如表14～表16 所示.

表14 专家E1 给出的二维二元语义评估矩阵Table 14 2-dimension 2-tuple linguistic information assessment matrix by E1

表14 专家E1 给出的二维二元语义评估矩阵Table 14 2-dimension 2-tuple linguistic information assessment matrix by E1

X1 X2 X3 X4 X5 A1 〈(s6,0),3.550〉 〈(s5,0),3.375〉 〈(s4,0),3.675〉 〈(s5,0),3.950〉 〈(s5,0),3.250〉A2 〈(s3,0),3.525〉 〈(s4,0),3.450〉 〈(s6,0),3.675〉 〈(s4,0),3.725〉 〈(s5,0),3.275〉A3 〈(s4,0),3.625〉 〈(s6,0),3.800〉 〈(s5,0),3.500〉 〈(s4,0),3.950〉 〈(s5,0),3.050〉

表15 专家E2 给出的二维二元语义评估矩阵Table 15 2-dimension 2-tuple linguistic information assessment matrix by E2

表15 专家E2 给出的二维二元语义评估矩阵Table 15 2-dimension 2-tuple linguistic information assessment matrix by E2

X1 X2 X3 X4 X5 A1 〈(s5,0),2.750〉 〈(s4,0),3.875〉 〈(s4,0),4.275〉 〈(s5,0),3.950〉 〈(s5,0),3.550〉A2 〈(s3,0),3.550〉 〈(s4,0),3.475〉 〈(s6,0),3.575〉 〈(s5,0),3.850〉 〈(s4,0),3.350〉A3 〈(s5,0),3.625〉 〈(s6,0),3.800〉 〈(s3,0),3.500〉 〈(s5,0),3.950〉 〈(s4,0),3.050〉

表16 专家E3 给出的二维二元语义评估矩阵Table 16 2-dimension 2-tuple linguistic information assessment matrix by E3

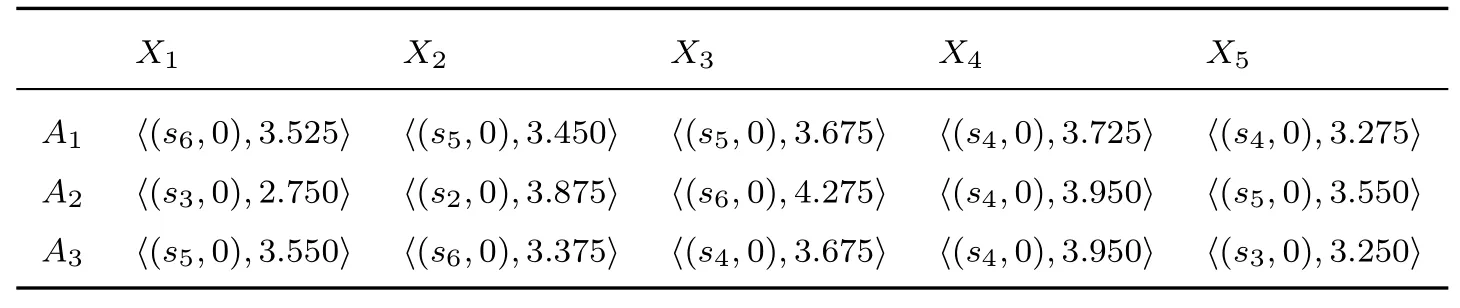
表16 专家E3 给出的二维二元语义评估矩阵Table 16 2-dimension 2-tuple linguistic information assessment matrix by E3

X1 X2 X3 X4 X5 A1 〈(s6,0),3.525〉 〈(s5,0),3.450〉 〈(s5,0),3.675〉 〈(s4,0),3.725〉 〈(s4,0),3.275〉A2 〈(s3,0),2.750〉 〈(s2,0),3.875〉 〈(s6,0),4.275〉 〈(s4,0),3.950〉 〈(s5,0),3.550〉A3 〈(s5,0),3.550〉 〈(s6,0),3.375〉 〈(s4,0),3.675〉 〈(s4,0),3.950〉 〈(s3,0),3.250〉

步骤3利用λh=计算可得决策者权重λ=(0.41,0.25,0.34).

步骤4由式(21)计算可得综合决策矩阵为

步骤5采用AHP 法计算属性的主观权重,采用熵值法计算属性的客观权重,然后通过式(22)求解得到组合权重,计算结果及分析如表17 所示.

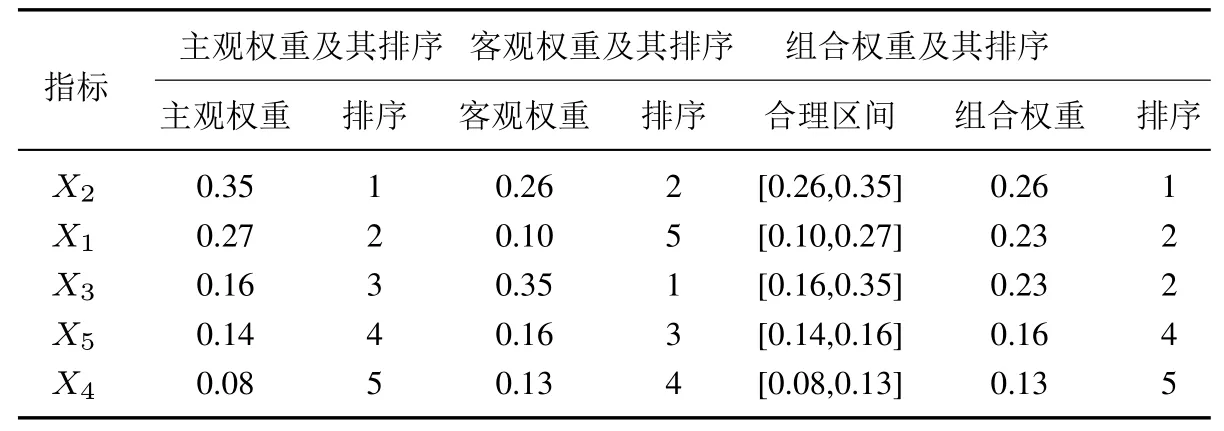
表17 主客观权重及组合权重Table 17 Subjective and objective weights&combined weights

步骤6根据式(23)可得每个方案的二维二元语义最终值,结果如表18 所示.

表18 二维二元语义最终值Table 18 The final values of 2-dimension 2-tuple linguistic information

根据式(24)可得三个方案的期望值E[A1]=0.668 4,E[A2]=0.4150,E[A3]=0.586 2.

由此可知,三个方案的优劣排序为A1≻A3≻A2,故A1(风能)为最优方案.

4.2 方法比较分析

为了进一步验证本文方法的优越性与合理性,采用文献[20]中所提出的二维二元语义群决策方法,与本文评价结果进行比较分析.基于传统的二维二元语义期望值函数和距离函数,根据本文所求得的权重信息,计算出各个方案的综合评价值,如表19 所示.

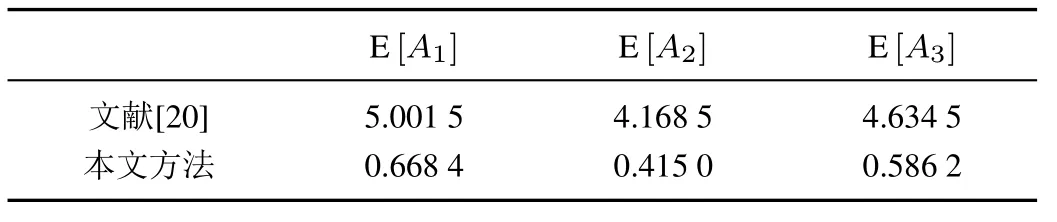
表19 不同方法评价结果对比Table 19 Comparison of evaluation results of different methods

由表19 可知, 基于文献[20]的方法计算得到的三个方案优劣排序结果为A1≻A3≻A2, 方案A1(风能)为最优方案,与本文方法所得结果一致,说明本文所提方法是有效的.但是,三个方案综合评价值的差值并不是很大,在进行方案选择时会对决策者造成不必要的干扰.这是由于文献[20]的决策方法所采用的二维二元语义期望值函数,其实质只是将一维、二维语言信息进行简单相乘,并没有考虑到第二维语言信息本身所存在的意义,据此改善模型所定义的二维二元语义在处理信息时就不够准确;其次,其所采用的语言评估标度也存在不合理之处,这就会进一步造成信息处理时的不精确.因此,与传统二维二元语义方法相比,本文方法在信息处理时更加精确,也更符合实际决策问题.

4.3 敏感性分析

属性权重在多属性群决策中起着至关重要的作用,由于属性权重确定方法存在着优劣之分,采用不同的属性权重计算方法就会得到不同的结果,这可能会对群决策结果造成一定的影响.因此,有必要对群决策结果进行敏感性分析.

针对上述算例,图2 给出了敏感性分析的结果.

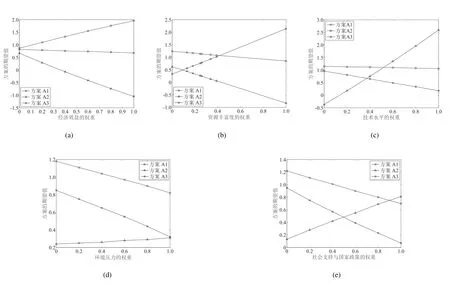
图2 指标权重对方案期望值的影响Fig.2 The influence of index weight on the expected value of the scheme

当改变某一指标的权重时, 其余指标权重按比例变化, 如表17 所示.各指标初始权重分别为经济效益0.225,资源丰富度0.26,技术水平0.225,环境压力0.13,社会支持及国家政策0.16.当经济效益的权重由0.225 变为0.5 时,其它指标权重之和为1−0.5=0.5.将该权重之和按比例分配给其它指标.例如,对于技术水平来说,wX3=0.5×0.225/(1−0.225)=0.145.

由图2 可知, 环境压力指标对选择决策没有敏感性, 无论其权重如何变化决策结果排序均为A1≻A3≻A2.经济效益指标对其权重变化表现出轻微的敏感性,除非当其权重减少到0.18 左右,否则优劣排序一直为A1≻A3≻A2,决策结果几乎不发生变化.与经济效益指标相似,社会支持及国家政策对其权重变化也表现出轻微的敏感性,除非当其权重增加到0.9 左右,否则均可选择A1作为最优方案.而技术水平指标和资源丰富度指标对其权重变化较为敏感,当技术水平指标权重增加到0.5 左右时,决策结果排序就变成A2≻A1≻A3;当资源丰富度指标权重增加到0.42 左右时,决策结果排序就变成了A3≻A1≻A2.这说明该问题中最敏感因素为技术水平指标和资源丰富度指标,即这两个指标是该决策问题的最关键指标.

5 结束语

本文针对群决策过程中存在的决策信息模糊和信息处理不够精确的问题,考虑到合理的语言标度更能符合专家的心理判断,提出了一种基于正态分布的二元语义表示模型,使得决策者能够给出更加合适、准确的评价信息.基于可信性测度的原理,给出了新的二维二元语义距离公式和期望值函数,进而解决信息在转换处理过程中的不精确性.通过可再生能源选择的算例分析验证了该方法的可行性和科学有效性.敏感性分析表明,属性权重的微小变化并不会导致决策结果的排序发生任何变化.这说明该方法具有较好的抗干扰能力,能够准确地选出最优方案.