结合半参数方法和贝叶斯抽样技术的多响应优化设计

汪建均, 郜婷玉, 杨世娟

(南京理工大学经济管理学院,江苏南京 210094)

1 引 言

响应面方法(response surface methodology,RSM)通常被认为是利用试验设计、响应模型和优化方法获取最优工艺参数的一种统计分析方法[1].统计学家Myers 等[2]曾明确指出“从更广泛的意义上看,响应曲面方法已经成为整个工业试验的核心”.随着顾客需求层次的多样化以及产品性能的稳步提升,在实际的产品与工艺过程中,往往需要考虑多个质量特性,因此多响应曲面优化设计问题在持续性质量改进活动中显示出越来越重要的作用[3−5].

多响应曲面优化设计通常包括试验设计、模型构建以及参数优化三个阶段,其中响应曲面模型构建至关重要[6].在多响应曲面优化设计中,研究者首先需要构建合适的度量指标.然而,由于涉及到多个质量特性,因此在度量指标构建中往往需要考虑多响应之间的相关性、模型参数的不确定性、预测响应的波动以及过程的稳健性[7].在多响应曲面的优化设计中,常见的优化策略是通过数据降维方法将多响应的优化问题转换为单一指标的优化问题,其中具有代表性的方法为:满意度函数方法、多元质量损失函数和后验概率方法等.比较而言,满意度函数方法简单实用,并且能够在一些常用统计软件如MINITAB 中加以使用,因此引起一些研究者和质量工程师的广泛关注.例如,He 等[8]综合考虑稳健性和最优性提出了一个新的满意度函数模型,有效地解决了传统满意度函数未考虑多响应优化过程的稳健性问题.然而,满意度函数方法难以有效地考虑多响应之间的相关性、预测响应的波动以及模型参数的不确定性.为此,一些研究者运用质量损失函数来实现多响应优化设计.例如,Ko[9]扩展传统多元质量损失函数,进一步地考虑多响应的预测性能和稳健性能,有效地兼顾过程的偏差、稳健性以及预测性能之间的平衡.然而,正如文献[9]中所指出的那样“所提出的多元质量损失函数未能考虑模型参数不确定性对优化结果的影响”.

在响应曲面建模过程中,研究者期望通过响应曲面模型来反映试验因子与多响应之间精确的函数关系,从而获得更为合理的参数优化结果.但是,正如著名统计学家Box[10]所言“所有的模型都是错误的,但是有些模型是有用的”.传统的响应曲面建模方法通常事先假定响应曲面模型结构,然后采用参数方法加以估计.然而,在很多情况下,所假设的响应曲面模型结构并不符合客观的实际情况,从而导致无法获得可靠的研究结果,甚至出现错误的研究结论.因此,在响应曲面模型构建过程中需要考虑模型不确定性(模型参数以及模型结构不确定)对优化结果的影响.为此,Peterson[11]在标准的多响应曲面(standard multi-response models,SMR)框架下利用贝叶斯方法考虑了模型参数不确定性对优化结果的影响,进而利用蒙特卡洛方法分析了优化结果的可靠性,即未来响应预测值落在产品规格限内的概率.Peterson 等[12]指出SMR 模型通常假设各个响应的模型结构是相同的,即模型所包含的因子效应是完全相同的.然而,在很多情形下响应模型所包含的因子效应往往是完全不同的.鉴于此,Peterson 等[12]在似不相关回归模型(seemingly unrelated regression,SUR)的框架下利用贝叶斯方法开展了多响应优化设计.针对多响应优化问题,汪建均等[13]在贝叶斯统计建模框架下利用SMR和SUR模型结合多元质量损失函数和后验概率方法,全面地考虑多响应之间的相关性、多元过程的稳健性、多目标之间的冲突以及优化结果的可靠性.上述响应曲面建模方法均事先对模型结构和响应分布等做出一些假设.然而,Min 等[14]指出“传统的参数回归方法通常需要在拟合响应曲面模型之前假设响应与因子之间的模型结构,这往往与实际情况并不相符,从而导致出现不可靠的研究结果,甚至是错误的研究结论”.比较而言,非参数方法不需要事先假定模型结构,而是利用试验数据本身所包含的信息自适应地拟合响应曲面模型,往往更加符合实际情况.因此,在多响应优化设计中,一些研究者尝试地利用非参数方法开展响应建模工作,并取得一系列的研究成果.Vining 等[15]认为参数模型不能较好的刻画方差模型与各因子间的关系.因此他们采用基于核估计的非参数方法构建均值模型与方差模型,并指出非参数方法所构建的响应曲面模型的预测性能要优于基于二阶多项式模型所构建的响应曲面模型.Ouyang 等[16]结合Bootstrap 方法和Pareto 优化提出一种集成的径向基函数(radial basis function,RBF)神经网络方法,并利用该非参数方法进行了参数优化设计.另外,一些研究者也考虑利用非参数方法对非正态响应的质量设计问题进行了研究.例如,Fox 等[17]利用非参数方法对非正态响应的试验设计进行了分析.针对具有重尾分布的非正态响应数据,Lim 等[18]结合平滑样条方法提出了一种基于非参数分位数回归的置信区间新方法,有效地解决上述非正态响应的质量设计问题.

虽然非参数方法不需要对模型结构进行事先的假设,从而在建模方面具有良好的灵活性,能够直接根据观测数据拟合响应的均值和方差模型.但是非参数方法往往依赖于相对大的样本或空间填充设计, 样本量偏小会可能导致响应波动较大.针对非参数方法的不足之处,一些研究者提出了一些能够处理小样本试验数据的半参数方法.因此, 基于半参数的多响应优化设计方法也引起一些研究者的广泛关注和兴趣.Wan[19]认为非参数方法对稀松数据进行响应曲面建模时,通常会导致其响应方差过大,并指出半参数方法则能较好地处理该问题.Pickle[20]通过比较三种方法(即参数方法、非参数方法和半参数方法)的均值模型和方差模型的均方误差值,验证了所提半参数方法的有效性.他们提出了两种半参数的建模策略,一种是模型稳健回归方法1(model robust regression 1,MRR1);另一种是模型稳健回归方法2(model robust regression 2,MRR2).在MRR1 中的组合成分中,一部分是响应的参数拟合项,另一部分是响应的非参数拟合项.该方法将这两项的权重和设为1,只要假设其中某一项为未知的混合参数即可.在MRR2 的组合成分中,一部分为响应的参数拟合项,另一部分则替换为非参数残差拟合.因此MRR2 默认参数项的权重为1,非参数项为小于1 的权重系数(即混合参数).其中,混合参数的选择是基于数据驱动的渐近最优值表达式.Mays 等[21,22]通过仿真方法来选择非参数模型的带宽和混合参数,从而获得更为稳健的半参数估计结果.此外,在该文献中,他们还给出了一种新的惩罚准则作为选择策略,并阐述了单独使用参数或者非参数方法的局限性.Mays等[23]对混合参数进行渐近最优估计和模型可靠性估计,并通过一个小型仿真实验验证了所提方法的有效性.Wan 等[24]提出了以期望函数为优化目标函数的多响应稳健回归方法,他们结合试验数据和仿真数据对参数方法和半参数方法进行了对比研究.研究结果表明: 与参数方法相比,基于半参数优化方法的偏差和方差都更低.

目前,基于半参数方法的多响应优化设计仍然存在一些问题没有得到很好地解决.例如,在多响应优化设计中,一些研究者往往没有考虑模型不确定性以及随机误差所引起的预测响应波动,从而导致获得不可靠甚至错误的研究结论.另外,由于多响应目标之间的冲突以及模型结构等不确定因素影响,其优化结果的可靠性(预测响应值落在所给定的规格限内的概率)也有待进一步研究.针对上述问题,本文结合半参数方法和贝叶斯抽样技术提出一种新的多响应优化方法.首先,通过半参数方法建立可控因子与响应之间的多响应面模型;其次,利用质量损失函数建立期望目标函数,同时通过贝叶斯抽样方法构建随机误差修正模型;然后,通过混合遗传算法对所构建的模型进行参数优化,获得最佳的参数设计值.最后,结合贝叶斯抽样技术对所获得参数优化结果进行稳健性评估,以考察其优化结果的可靠性.

2 非参数和半参数建模方法

当模型结构错误设定时,传统的参数回归方法可能会造成试验数据拟合不合理.尤其是当研究问题比较复杂、模型不确定性较高时,这种模型拟合不恰当问题就更加突出.因此Anderson-Cook 等[25]提出了采用局部回归思想的非参数方法对试验设计进行拟合,以应对较为复杂的稳健参数设计问题.在通常情况下,在无法确定输入因子与输出响应之间的函数关系时,分析人员可以采用数据驱动方法来局部回归拟合响应曲面模型.由于数据驱动方法不仅可以拟合线性模型也可以拟合高度复杂的非线性模型,因此基于数据驱动的非参数或半参数方法可以较好地构建稳健的响应曲面模型,从而能够处理高度复杂的响应曲面优化设计问题.

2.1 非参数响应曲面建模

非参数方法是基于数据驱动的响应曲面建模方法,其回归函数的形式和随机误差分布都不作严格要求.针对某一点的估计值,那些接近该点的响应通常假设比那些远离该点的响应包含更多的信息.因此,为了得到一个光滑的函数,一些非参数方法会使用局部加权平均原理.局部平均的基本思想等同于寻找局部加权最小二乘估计量的过程.若无法确定响应曲面模型的具体形式,分析人员通常会考虑利用非参数方法进行响应面建模.非参数无需事先设定模型函数的基本形式,因此更加符合实际情况.常见的非参数方法有核函数回归、局部多项式回归和样条回归等方法.其中,局部多项式回归本质上是核函数回归的一种拓展.

非参数方法通常使用局部线性回归(local linear regression,LLR),其中LLR 是1 阶多项式回归.非参数估计关键在于如何确定核函数.核函数的形状和值域可以反映响应估计值f(x0)在估计点x0处所用到数据量的权重.由于核函数方法不利用有关数据分布的先验知识,对数据分布也不附加任何假定,是一种从数据本身出发研究数据分布特征的方法.

针对需要预测的点x0=(x01,x02,...,x0k),核函数可以定义为

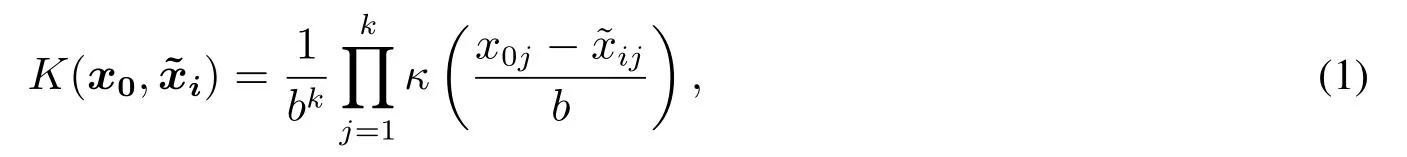
当对均值或者方差模型都使用非参数方法时,由于影响这两种不同模型的控制因子可能不同,一般对均值模型使用二阶模型,对方差模型使用一阶模型,所以将使用不同的核函数.常见的核函数为高斯函数、均匀函数和三角函数等.根据Simonoff[26]的研究,核函数的变化并不会对估计值有很大的影响,所以本文将使用以往文献中最为流行的高斯核函数,其形式为κ(u) = e−u2.K(x0,)中估计函数的平滑性取决于带宽参数b.Mays 等[21]提出了新的惩罚预测误差平方和技术(penalized prediction error sum of squares,PRESS∗∗)进行合适的带宽选择,通过最小化PRESS∗∗的函数值来寻求带宽b的最优值.这里

其中SSEmax代表所有可能带宽值下的最大误差平方和;SSEb是指特定某个带宽值下的误差平方和;k是回归因子的个数, 一般是控制变量的个数; 分子部分是预测误差平方和(prediction error sum of squares,PRESS).

留一法是指交叉验证方法的一种, 假设样本数据集中有N个样本.将每个样本单独作为测试集, 其余(N −1)个样本作为训练集,这样得到了N个分类器或模型,用这N个分类器或模型的分类准确率的平均数作为此分类器的性能指标.每一个分类器或模型都是用几乎所有的样本来训练模型,最接近样本,这样评估得出的结果与训练整个测试集的期望值最为接近;HLLR是非参数方法LLR 得到的平滑矩阵

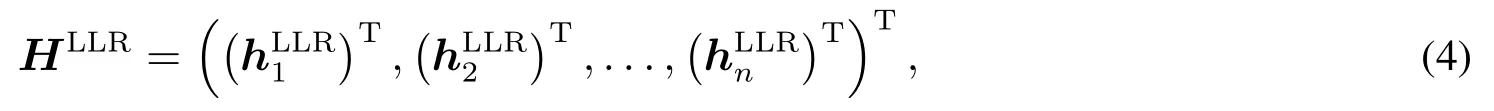
非参数方法具有良好的灵活性,能够直接根据观测数据拟合均值响应模型,但是这些拟合模型往往具有较高的方差.非参数方法往往依赖于相对大的样本或空间填充设计.与非参数方法不同的是,半参数方法并不要求大量的样本.在此,将重点介绍两种常见的半参数方法.

2.2 半参数响应曲面建模

半参数方法顾名思义,就是结合传统的参数方法和基于数据驱动的非参数方法的一个组合模型方法.针对以往的传统参数方法无法处理: 第一,对基础模型只有部分了解;第二,数据本身波动较高.这种情况下,用参数方法进行模型估计其误差会较大.虽然非参数方法可以较好地处理上述问题,但是非参数方法对试验数据的样本量有较高的要求.半参数方法则可以充分发挥二者的优势,较好地解决模型结构不确定和试验数据样本量小的问题.参数方法通常使用经典的最小二乘法OLS 进行参数估计,非参数方法则采用局部线性回归LLR 进行估计,因此通过将传统的参数估计和基于数据驱动的非参数方法进行有机整合就可以构成半参数方法.在此,将介绍两种经典的半参数方法.

2.2.1 MRR1 方法

Robinson 等[27]提出了一种考虑均值响应建模的半参数方法,即通过一个混合参数λ结合参数和非参数部分.则可构建混合模型

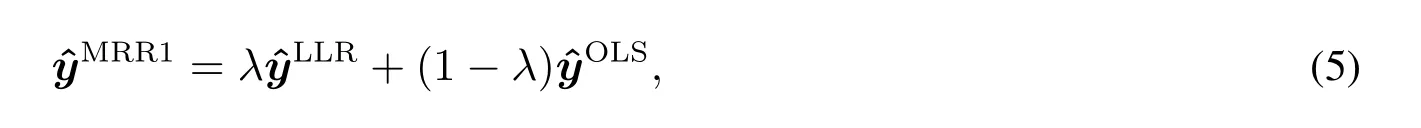
其中第一部分是通过非参数回归得到的拟合向量和混合参数λ的乘积,第二部分是参数回归得到的拟合向量和剩余比例部分的乘积.MRR1 通过给参数部分和非参数部分分配比例系数得到半参数模型,但是这种组合模型的波动在以往文献中被证实较高,其中λ ∈[0,1]而这个λ的选择法,类似于非参数部分的带宽b的选择,本质上是一种偏度方差的平衡,混合参数λ的渐近最优值用下面的数据驱动表达式来求得,即

该半参数方法可以通过平滑估计获取数据中的异常信息.此外,MRR1 方法不仅可以弥补参数方法整体拟合偏差大的问题,而且能够处理非参数方法过度拟合的局限性,从而带来响应面设计的稳健性.如果参数部分估计和非参数部分估计同时较高或者较低,MRR1 估计也会过高或者过低.因此,有必要引入MRR2 半参数方法以纠正上述错误.

2.2.2 MRR2 方法

MRR2 方法是Mays 等[22]通过改进MRR1 方法获得一种新的半参数方法.与MRR1 方法比较而言,MRR2 方法在建模组合策略上有所不同.第一,MRR2 方法将对参数方法得到的残差进行非参数处理,得到非参数残差部分.然后,将非参数残差部分和参数拟合部分进行组合.第二,MRR1 将非参数和参数部分各自设定未知的权重系数,权重和为单位1.而MRR2 方法则将参数拟合部分权重赋值为1,非参数残差部分权重用混合参数λ(λ ∈[0,1])表示.在MRR2 方法中,参数拟合也是利用最小二乘方法进行拟合;非参数方法则是对参数拟合与真实响应值的残差进行非参数拟合.所谓参数拟合和真实响应的残差是指参数拟合无法获取的数据结构,而本节的非参数拟合是指通过LLR 来对上述残差进行拟合,其混合模型为

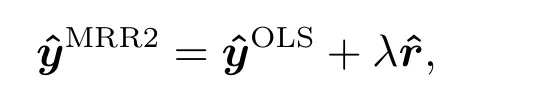
类似于MMR1 中的λ的求法,λ ∈[0,1],λ的大小并不像上一节方法可以反映模型错误估计的程度,而是指表示残差拟合需要的校正量.当λ= 1 时表示非参数拟合和参数拟合所占的比重一样.渐近最优估计的λ表达式为根据以往文献发现,关于响应估计的期望,一般认为MRR2 的效果比MRR1 的效果更加好.因此,本文将倾向于使用MRR2 方法进行参数估计.

3 本文所提方法

3.1 考虑重复试验的非参数响应曲面建模

在多响应优化设计中,若无法根据试验设计数据获得响应曲面模型的结构时,采用传统的参数回归方法进行均值响应曲面建模则可能会引起较大的偏差,即造成较大的模型误差.鉴于上述情况,引入非参数方法来构建响应与试验因子之间的响应曲面模型,其具体模型为

其中响应预测值是由非参数拟合部分h(xi)和误差部分εi组成,其中εi ～N(0,1).

若试验在每个处理(即试验方案)下都存在重复试验时,可以借鉴双曲面建模思想利用非参数方法来构建基于响应均值和方差的双响应曲面模型.结合上一节的非参数响应曲面建模知识,本文选择相对简单的局部多项式回归非参数方法,其中核函数选择常用的高斯核函数κ(u)=e−u2.上述核函数的带宽b可以利用式(2)通过最小化PRESS∗∗来获得.

针对具有重复试验数据的多响应优化问题,利用非参数模型(即式(9))来分别拟合各响应方差以及这些响应之间的协方差与试验因子x的函数关系.在此基础上获得响应方差–协方差函数Σy(x)与试验因子x之间的关系.另外,利用重复试验数据获得每个试验点的样本均值,然后利用非参数模型即式(9)拟合响应均值与试验因子之间的响应曲面模型,即均值函数E[y(x)].在此基础上,利用多响应的质量损失函数构建本文所提方法的优化模型,即

其中θ代表目标值矩阵,C代表成本矩阵.

具体的非参数响应面方法的步骤如下:

步骤1根据PRESS∗∗函数代码迭代从候选列表中找出最优带宽值b.

步骤2代入期望质量损失函数,利用遗传算法参数优化,得到最佳参数水平值.

步骤3部分试验结果会受到噪声因子的影响使得结果的可靠性降低.为了对结果的可靠性评估,利用随机抽样(蒙特卡罗抽样),统计落在规格限内的样本数目,从而能够评估优化结果的可靠性.

3.2 结合贝叶斯抽样技术的误差修正模型

有重复试验数据的情况下,基于半参数方法的多响应曲面模型一般可假设为

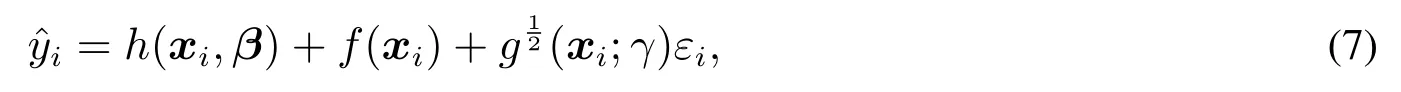
其中h(xi,β)代表参数方法部分,f(xi)代表的是非参数部分,是对方差模型的转换,εi是指随机误差.

然而上述做法存在三个不足之处: 一是重复试验成本较高;二是试验数据的随机误差假设服从标准正态分布即εi ∈N(0,1)可能与实际情况并不相符,无法真实地反应模型随机误差的分布特征;三是上述模型仅仅在具有重复试验数据情况才能构造出方差模型.若试验数据没有重复的情况下,则需要进一步考虑如何构造合适的统计量来刻画响应曲面模型的随机误差部分.

借鉴参考文献[13]中利用贝叶斯抽样方法获取随机误差项的思想,本文将对式(7)中的随机误差项进行修正,其具体模型为

其中W ∈N(0,H−1),v=N −p −q+1,H=在式(12)中,其随机误差项为

在此,本文拟结合半参数建模思想和贝叶斯抽样方法,将式(8)中Bz(x)运用式(7)中半参数方法进行拟合.上述处理方法能够充分利用半参数方法的优势,如能够有效地处理小样本试验数据等.需要特别指出的是,式(11)中随机误差项将在新模型中用式(12)的随机误差项所替代.利用贝叶斯抽样技术进行误差修正后的响应曲面模型为

其中v是自由度,N是样本大小,W是一个具有零均值向量和方差协方差矩阵为H−1的多元正态随机变量.z(xi)是观测点的q×1 的观测值,其中X是二阶因子模型矩阵,Y是N ×p响应值矩阵.ˆB是拟合系数向量,Z是由N个z(xi)向量形成的q×N矩阵.U是一个自由度为v不依赖于W的卡方随机变量.

在上述响应曲面模型的框架下,结合双响应曲面建模思想[25]分别构建出响应均值和方差模型,然后利用多元质量损失函数获得期望目标函数为

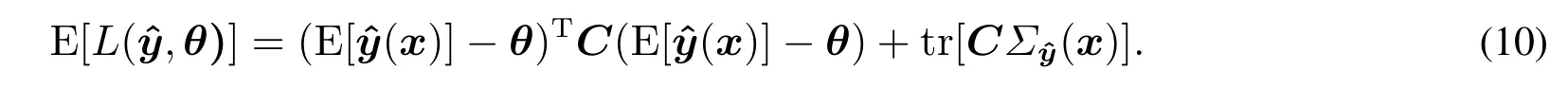
式(10)本质上是采用组合建模的思想所构建的一种新模型.该模型整合了试验者根据经验所设定的参数模型与适应试验数据特点所估计的非参数模型二者的优势.在此基础上,利用贝叶斯方法对模型误差的修正则进一步提升了所构建模型的预测能力.此外,该模型还兼容了半参数方法和贝叶斯方法的特点,能够有效地处理小样本试验数据的问题.因此,与以往的研究方法比较而言,基于数据驱动建模思想的响应曲面模型,能够更好地提取试验数据的特征,构建更为精确、更加符合实际的响应曲面模型.

3.3 基于混合遗传算法的参数优化

由式(7)～式(10)可知,结合半参数方法和贝叶斯抽样方法所构建的响应曲面模型往往具有高度复杂的非线性特征,传统的优化方法(如线性规划、梯度优化等)将难以获得可靠的优化结果[28].为此,借鉴文献[1,13],利用结合遗传算法和模式搜索法的混合遗传算法对上述目标函数即式(10)进行参数优化.与传统的优化方法比较而言,混合遗传算法有效地利用遗传算法良好的全局搜索能力和模式搜索方法突出的局部优化能力,因此利用该方法能够有效地处理高度复杂的参数优化问题[29].

3.4 评估优化结果的可靠性

在多响应曲面优化设计中,由于模型不确定性以及随机误差等因素的影响,将会导致输出响应呈现出相当大的波动.在这种情形下,如何衡量预测响应波动对优化结果的影响,如何评估优化结果的可靠性成为一项亟待解决的研究课题.为此,一些研究者提出一些评估优化结果可靠性的研究方法.其中,最具有代表性的是贝叶斯后验概率方法[11].该方法的核心思想是在贝叶斯响应曲面建模框架下,利用贝叶斯抽样方法计算预测响应值(即在最优参数设计值下的响应预测结果)落在其规格限内的概率,从而据此度量优化结果的可靠性.在给定的试验数据data 和响应规格限A下,其最优参数设计结果的贝叶斯后验概率的计算式为

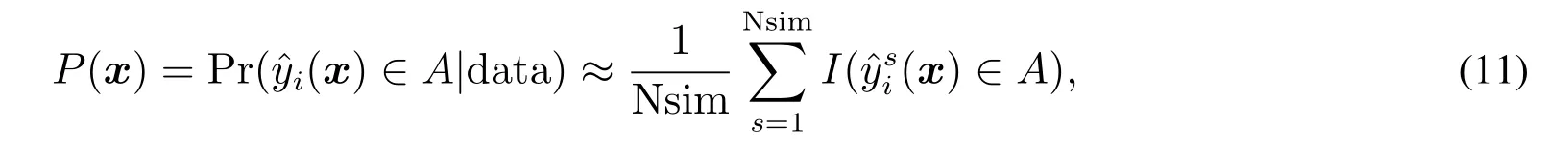
其中Nsim 代表响应模拟抽样次数,I(·)为示性函数.

当响应模拟抽样值落在规格限内时其后验概率结果P为1,否则为0.

在多响应优化设计中,在试验响应个数较多时,式(11)将是一个非常复杂的高维数值积分问题.此外,在很多情况下,其响应的密度函数往往非常复杂,甚至难以直接获得.因此,在这种情况下,通过贝叶斯模拟抽样方法将会大大地降低问题的难度和计算的工作量.需要特别指出的是,上述贝叶斯后验概率方法不仅适用于单响应参数优化问题,而且也可以拓展到多响应曲面的参数优化问题.在多响应优化设计中, 通过式(11)不仅可以获得单个响应预测值的边际后验概率值,而且也可以获得多个响应预测值落在其对应规格限内的联合概率概率值.

3.5 本文所提方法的实施步骤

针对多响应曲面优化设计中存在的问题,本文结合半参数方法和贝叶斯抽样模拟技术,提出一种新的建模与优化技术,其具体的实施步骤如下:

步骤1首先对原始数据进行普通最小二乘法(OLS)拟合分别得到关于两个响应的参数拟合值,然后通过原始响应构建残差向量,将残差向量再利用PRESS∗∗函数寻求最佳的带宽值b.

步骤2根据半参数模型公式中的非参数部分,利用LLR 方法对上述步骤2得到的两组残差向量分别进行非参数拟合得到两组非参数拟合的拟合残差向量.

步骤3通过步骤1 和步骤2 中分别得到的OLS 拟合值和非参数残差拟合值.利用MRR2 方法中的混合参数构造方法——函数,分别得到对应响应的最合适的混合参数值λ.结合OLS 拟合值、残差拟合值和混合参数λ将非参数响应曲面模型扩展为半参数响应曲面模型.

步骤4借鉴参考文献[13]中利用贝叶斯抽样方法获取随机误差项的思想进行误差修正,同时利用半参数的响应建模方法对响应曲面进行重新拟合.最后,综合上述两个方面的改进提出一种基于误差修正的响应曲面模型,并在此基础上利用多元质量损失函数构建出本文所提方法的优化目标函数.

步骤5利用混合遗传算法对步骤4 中所获得期望质量损失函数进行参数优化,获得最优的参数设计值.

步骤6利用贝叶斯后验概率方法对参数优化结果的可靠性进行评估.

4 实例分析

该实例来源于文献[13],其主要目的是对一种聚合物进行参数优化设计,以寻找最佳的设计参数值.在该试验中,可控因子为反应时间x1(reaction time)、反应温度x2(reaction temperature)和催化剂的用量x3(amount of catalyst).试验的输出响应是转化率y1和热活动y2.其中,转化率为望大类型的质量特性(y1∈[80,100]),目标值θ1假定为100;而热活动为望目的质量特性(y2∈[55,66]),其目标值θ2假定为57.5.在整个试验的分析过程中,假设回归模型中因子效应所构成的向量为z(x) = (1,x1,x2,x3,x1x2,x2x3,x1x3,x21,x22,x23).在该试验中,试验者选择中心复合设计(central composite design,CCD)开展相关的试验,其聚合物试验的因子计划安排、响应的输出结果如下表1 所示.

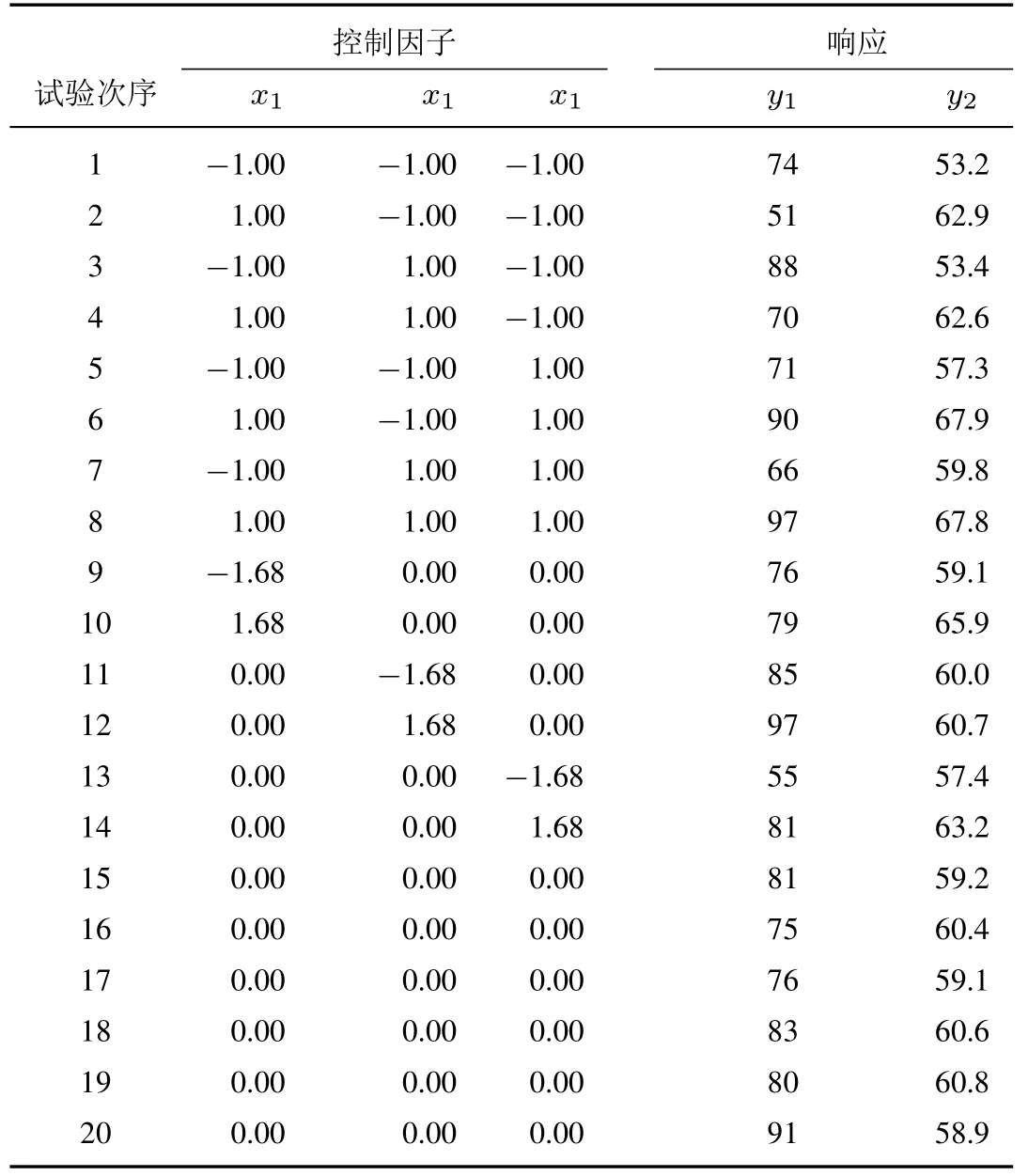
表1 某聚合物的试验设计结果Table 1 The experimental design results of a polymer

根据第3.5 节中所提出的实施步骤,结合上述表1 所获得可控因子与输出响应的试验数据,在此利用半参数建模方法进行响应曲面建模.其中非参数方法中核函数选择为高斯核函数,其最佳带宽值b(其中两个响应关于带宽的PRESS∗∗函数如图1,图2 所示)分别为0.68 和0.35,最佳混合参数值为1.

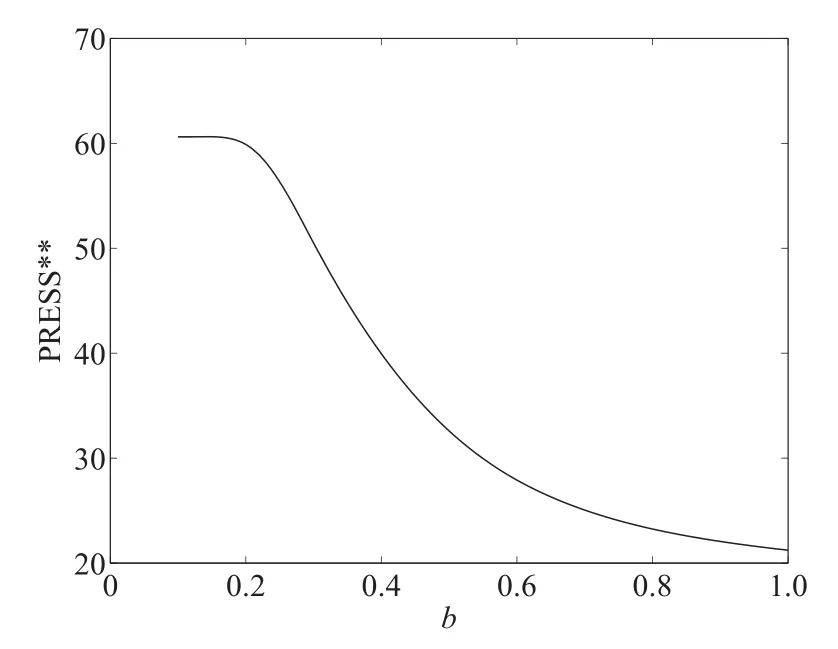
图1 响应值y1 的PRESS∗∗函数图Fig.1 PRESS∗∗function diagram of response y1

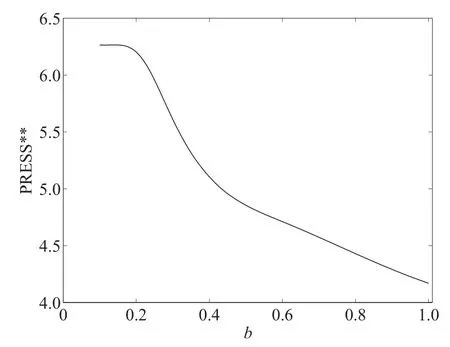
图2 响应值y2 的PRESS∗∗函数图Fig.2 PRESS∗∗function diagram of response y2

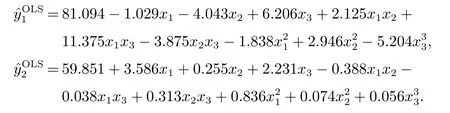
然后,利用第3.3 节中所介绍的混合遗传算法对所提出的期望质量损失函数进行参数优化,其参数优化结果为x1=−0.050,x2=1.682,x3=−0.063.同时,在最优位置点处的期望质量损失为13.834,贝叶斯后验概率为0.813 8.若采用文献[13]方法对该聚合物试验进行分析可知,其期望质量损失函数为14.663 6,同时其贝叶斯后验概率(即蒙特卡洛的抽样值落在给定规格限内的概率)为0.602 8.与文献[13]研究结果比较而言,本文所提方法在期望质量损失和后验概率值(该指标反映产品符合规格的程度)均表现出一定的优势,其主要原因是文献[13]方法事先假设固定的模型结构,从而忽视模型结构不确定性对优化结果的影响.正如文献[13]中曾指出的那样,模型结构的变化可能会低估或高估其综合性能评价指标(如期望质量损失函数或贝叶斯后验概率).此外,为了进一步验证所提方法的有效性,本文还将文献[11]的贝叶斯后验概率方法、文献[10]的多元质量损失函数方法、文献[20]中提到的非参数、文献[20]中提到的半参数方法运用到该聚合物试验的参数优化过程中,其优化结果如表2 所示.与文献[20]中的非参数方法和半参数方法两种方法比较而言,本文所提方法在期望质量损失函数和规格限内的概率两个评估指标上均优于上述两种方法的优化结果.因此,本文所提方法不仅在期望质量损失方面有所降低,而且在考虑产品的符合性概率方面也获得了较大的提升.

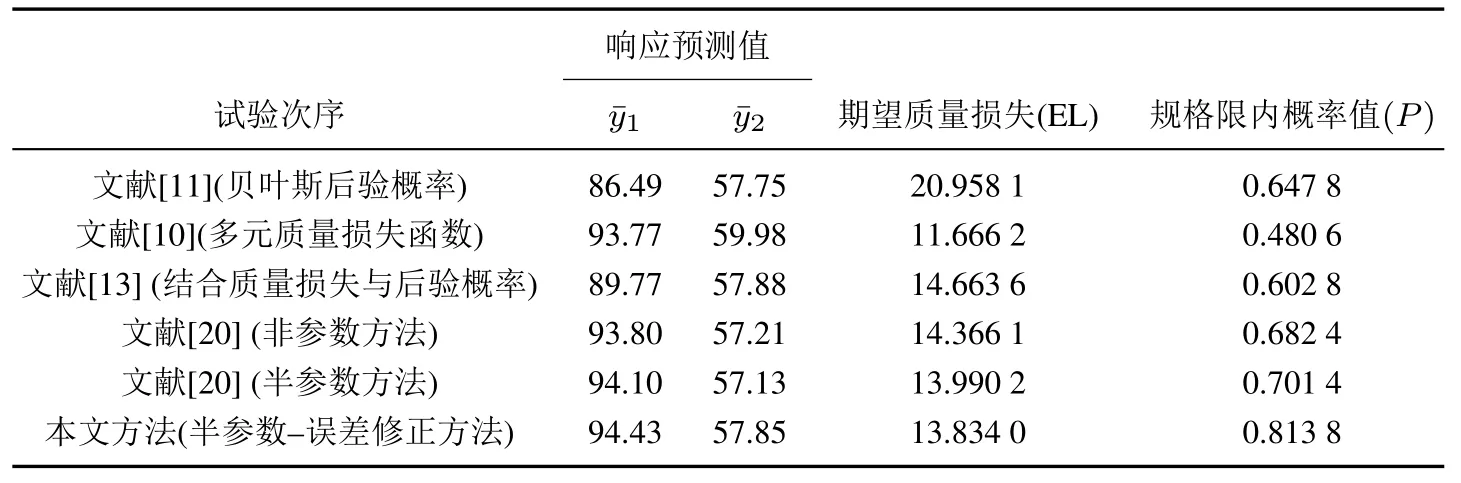
表2 优化结果指标对比表Table 2 Comparison table of optimization results

此外, 为了进一步验证参数优化结果的可靠性, 在最优参数设计值下利用所构建的响应模型进行10 000 次随机模拟抽样.考虑到样本间的自相关性,每间隔4 个抽样点抽取一次,最后获得了2 000 次的响应抽样值,其两个响应y1和y2抽样值的踪迹图如图3 和图4 所示.

在图3 中,其两条红线分别代表响应y1的规格上限100 和规格下限80.由于响应y1为望大类型的,因此其响应目标值假设为100,目标值红线和上限红线重合.另外,在图4 中,其响应y2的规格上限和下限分别为55 和66.图4中间的红线代表响应y2的目标值,即为57.5.从图3 和图4 可知,由于随机误差等确定性因素的影响,上述两个响应的抽样值围绕着某个确定的均值呈现上下随机波动的趋势,且其波动幅度基本保持一致,呈现出稳态分布的特征,因此可以利用其响应抽样值来评估其参数优化结果的可靠性.根据上述抽样结果,可以计算得出两个响应抽样值落在其对应的规格限内的概率分别为0.845 2 和0.956 6.上述的研究结果进一步证实参数优化结果的可靠性.

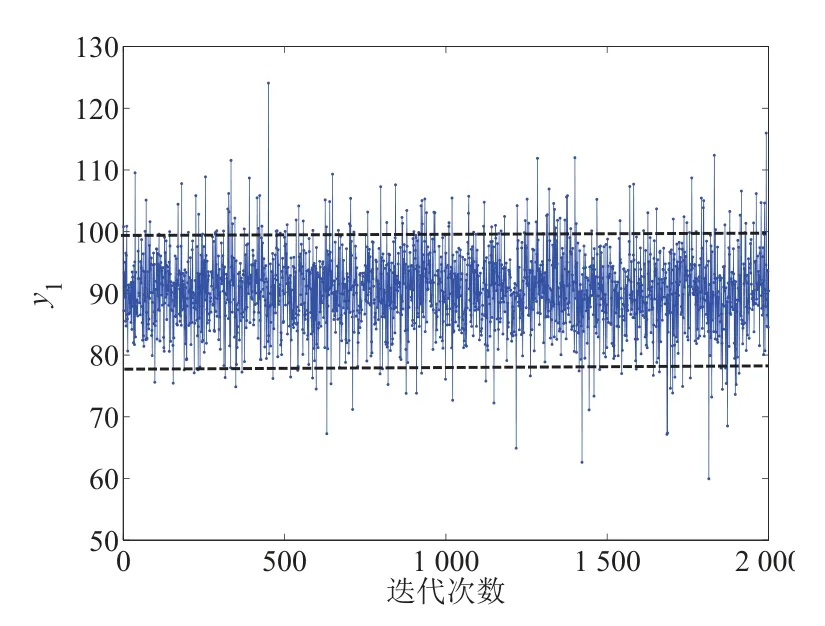
图3 响应值y1 的轨迹图Fig.3 Trace plot of response value y1

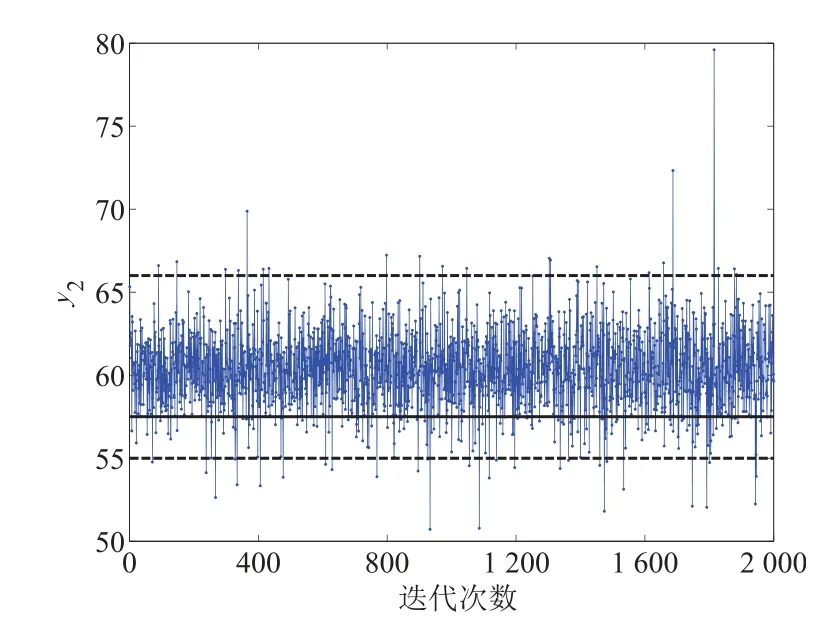
图4 响应值y2 的轨迹图Fig.4 Trace plot of response value y2

5 结束语

本文利用半参数方法建立过程响应与可控因子的响应曲面模型,并在此基础上结合贝叶斯抽样方法对所构建的响应曲面模型进行误差修正,从而获得更加精确、更加符合实际情况的响应曲面模型.此外,本文还利用贝叶斯后验概率方法进一步地评估了参数优化结果的可靠性.需要特别指出的是,若根据工程背景或专家知识能明确给出响应曲面模型结构时,则使用参数回归方法往往能够获得理想的模型估计结果.然而,若模型结构无法确定,则采用非参数或半参数方法等数据驱动方法往往能够获得更为可靠的响应曲面模型.

此外,未来的产品质量设计还需要从产品全生命周期视角全面地分析与思考.例如,在产品设计阶段,考虑通过互联网让广大客户参与产品质量设计,让所制造出的产品全面反映客户需求,真正做到高度客户化;在产品生产阶段,考虑利用物联网与传感器、以及人工智能技术,对生产过程进行实时质量监控与反馈,及时采集生产过程中环境(如温度、湿度)、设备故障等数据信息,然后利用大数据分析技术对所收集到的上述数据进行全面地分析,探寻可能影响最终产品设计质量的关键因素并加以优化;在产品售后以及使用阶段,充分地利用互联网或物联网及时收集客户在使用中所发现的潜在质量问题,或客户在维修保养过程中存在的产品质量问题,然后结合大数据分析技术寻求潜在的原因,并在未来产品质量设计中逐步加以改进和完善[30].因此如何结合互联网、人工智能与大数据分析技术开展产品质量设计技术与方法将是未来有待进一步研究的重要课题.